多波束分时压制干扰建模与仿真*

戎 华 陈 求

(海军大连舰艇学院 大连 116018)



多波束分时压制干扰建模与仿真*

戎 华 陈 求

(海军大连舰艇学院 大连 116018)

多波束分时压制干扰能够利用有限的干扰资源对多批威胁目标实施干扰,但由于采用了波束切换体制设计,会出现脉冲丢失的现象,影响多目标压制干扰效果。文章分析了脉冲丢失原因,建立了多波束分时压制干扰模型,并仿真分析了复杂电磁环境条件下,干扰脉冲持续时间和辐射源重频对压制干扰概率的影响,给出了压制干扰概率下降程度,对多目标分时压制干扰决策具有参考价值。

多波束分时压制干扰; 脉冲持续时间; 脉冲丢失; 压制概率

Class Number TP391

1 引言

多波束分时压制干扰通过电子侦察,依据目标威胁等级进行干扰排序,通过对辐射源信号的脉冲到达时间预测和干扰波束的瞬时切换实现对多目标的动态干扰。这种设计体制一定程度上将有限的干扰资源进行了最优化利用,同时也在波束切换过程中出现了脉冲丢失现象,影响了干扰效果。但目前的研究还停留在对脉冲丢失概率的建模分析[1,10],本文在分析脉冲丢失概率的基础上,进一步对多波束分时压制干扰概率进行了建模仿真。

2 分时压制干扰建模

干扰机对多目标辐射源进行压制干扰是通过分时波束切换实现的,某一特定时刻干扰机波束只能干扰一个辐射源,因此,在计算出“一对一”[2～3]压制干扰概率后,再将脉冲丢失概率折算到其中,就可以得到某一时间段内的“一对多”压制干扰概率。2.1 单目标压制干扰建模[4～5]

单部干扰机在某一时间间隔内对目标雷达“一对一”的压制干扰概率可以表示为

(1)

(2)

式中,fr为雷达脉冲重复频率；y0为检测门限；Pt为雷达发射功率；Gt为雷达发射天线增益；σ为目标的有效反射面积；Δfj为干扰机的通频带；φ为雷达扫描扇角；L为雷达功率损耗因子；K为波尔兹曼常数；Δfr为雷达接收机的通频带；Pj为干扰机发射功率；Gj为干扰机天线主瓣方向上的增益；θ0.5为雷达天线半功率波束宽度；θ(t)为雷达与目标连线和雷达与干扰机连线之间夹角；Rj(t)为干扰机至雷达的距离；R(t)为被掩护目标至雷达的距离,干扰机、 被掩护目标、 雷达的位置关系如图1所示[6～7]。

设敌机抵达攻击位置的距离为R0,即干扰任务的终止分配时刻为t2,敌机速度为v,干扰机坐标为(xj,yj,0),则有：

(3)

(4)

(5)

设φ为敌机航向与x轴夹角,则有：

(6)

(7)

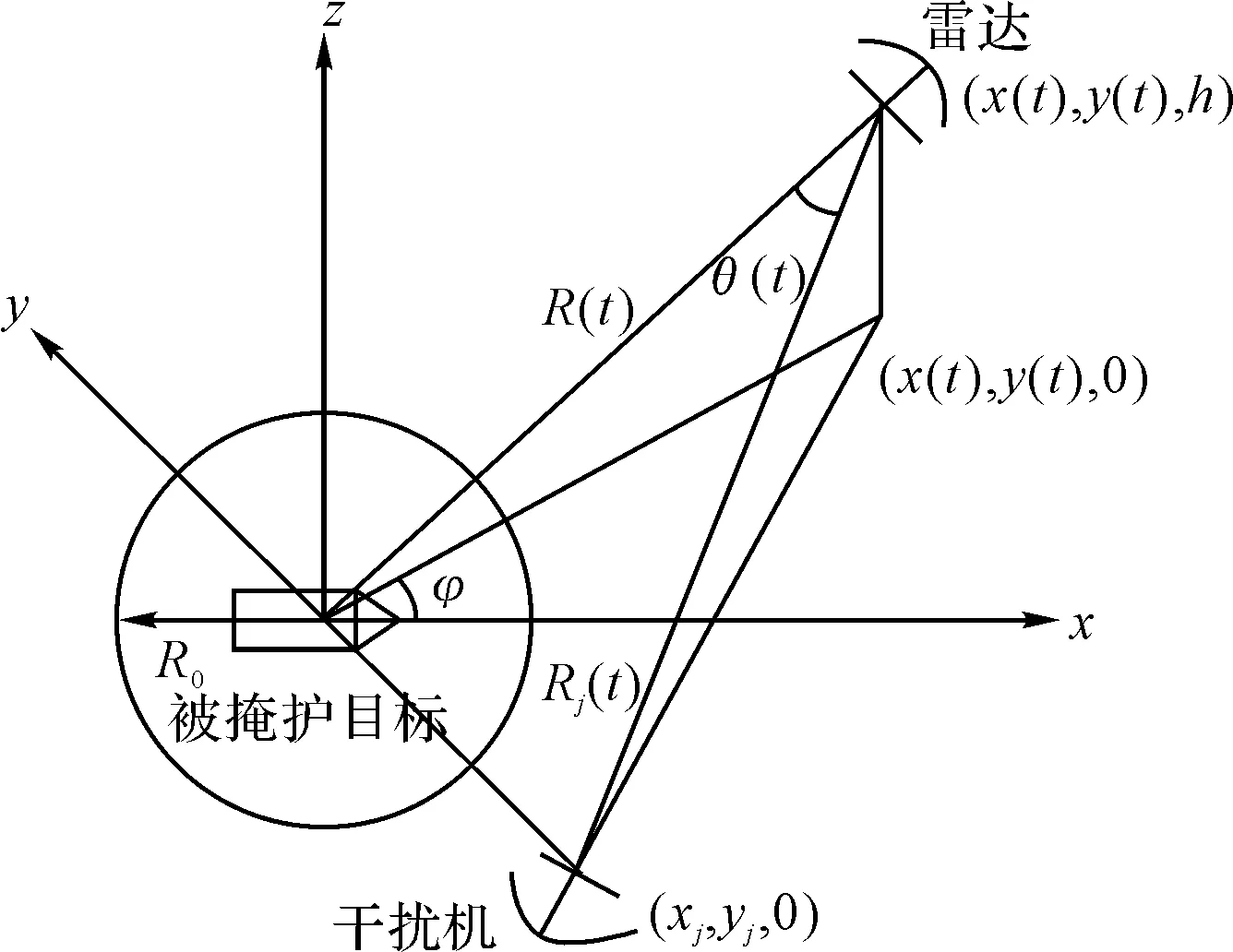
图1 干扰机、雷达、被掩护目标之间的位置关系图

2.2 多目标压制干扰建模

2.2.1 影响分时压制效果因素分析

对图2进行分析可知,单部干扰机在对多个雷达目标实施干扰时,主要分为三个时间段： 1) 对f1的干扰持续时间τ1,当多个辐射源的脉冲信号同时出现时,必然会出现脉冲重叠,在τ1时间段内,干扰机无法对其他不同频率的脉冲信号实施干扰,产生脉冲丢失； 2) 波束切换时间τ2,在此时间段内,如有辐射源脉冲信号出现,干扰机无法对其进行干扰,也会产生脉冲丢失； 3) 干扰侦察时间(包括实施干扰和侦察的相互转换时间)τ3,在此时间段内如有辐射源脉冲信号出现,干扰机无法对其进行干扰,也会产生脉冲丢失。以上产生的脉冲丢失现象,由于丢失的脉冲没有被有效干扰,从而影响了整体的干扰概率,是造成多目标分时压制干扰效果下降的重要原因[8]。

2.2.2 脉冲丢失概率计算

1) 干扰持续时间τ1内脉冲丢失概率[9～10]

当单部干扰机对多个辐射源目标实施分时压制干扰时,可以认为各辐射源的脉冲到达时间在统计概率上是相互独立不相关的,在τ1内到达的n个脉冲的概率服从泊松(Poisson)分布,即：

(8)

式中,ρ为平均脉冲密度。则在τ1时间内出现多于一个脉冲达到的概率Pn>1(τ1),即τ1时间内脉冲丢失的概率可表示为

Pn>1(τ1) =P2(τ1)+P3(τ1)+…

=1-(1+ρτ1)exp(-ρτ1)

(9)

2) 波束切换时间τ2内脉冲丢失概率

在脉冲波束切换时间内由于出现新脉冲,干扰机不能对新出现脉冲实施干扰,因此,在τ2和时间内脉冲的丢失概率Pn≥1(τ2)可表示为

Pn≥1(τ2)=1-exp(-ρτ2)

(10)

3) 干扰侦察时间τ3内脉冲丢失概率

在电子侦察和电子干扰的相互转换时间内,干扰机同样无法对新出现的脉冲实施干扰,因此,在τ3和时间内的脉冲丢失概率Pn≥1(τ3)可表示为

Pn≥1(τ3)=1-exp(-ρτ3)

(11)

4) 干扰机实施多目标干扰时总脉冲丢失概率

PL=Pn>1(τ1)+Pn≥1(τ2)+Pn≥1(τ3)

(12)

干扰机实施多目标干扰时,总脉冲的丢失概率反映了相较于干扰机实施单目标干扰的干扰效果下降程度。

2.2.3 多目标分时压制干扰概率

在实际海战场环境下,被干扰雷达辐射源的重频、脉宽以及干扰时所采用的带宽都不相同,通过计算机仿真可以得到单部干扰机对多目标实施分时压制干扰时的脉冲丢失概率,如果将脉冲丢失概率折算到干扰机的功率损耗,则当干扰机对N部雷达辐射源实施分时压制干扰时,对某一部雷达辐射源的压制概率可表示为

(13)

γ=1-ηPL

(14)

式中,γ为多目标分时压制干扰下的功率损耗因子,η为修正系数,由装备试验确定。

3 建模仿真流程

对多波束分时压制干扰的数学模型,可以通过计算干扰机对多个辐射源目标进行分时压制干扰的压制概率得出,计算机建模仿真可按图2所示流程进行。

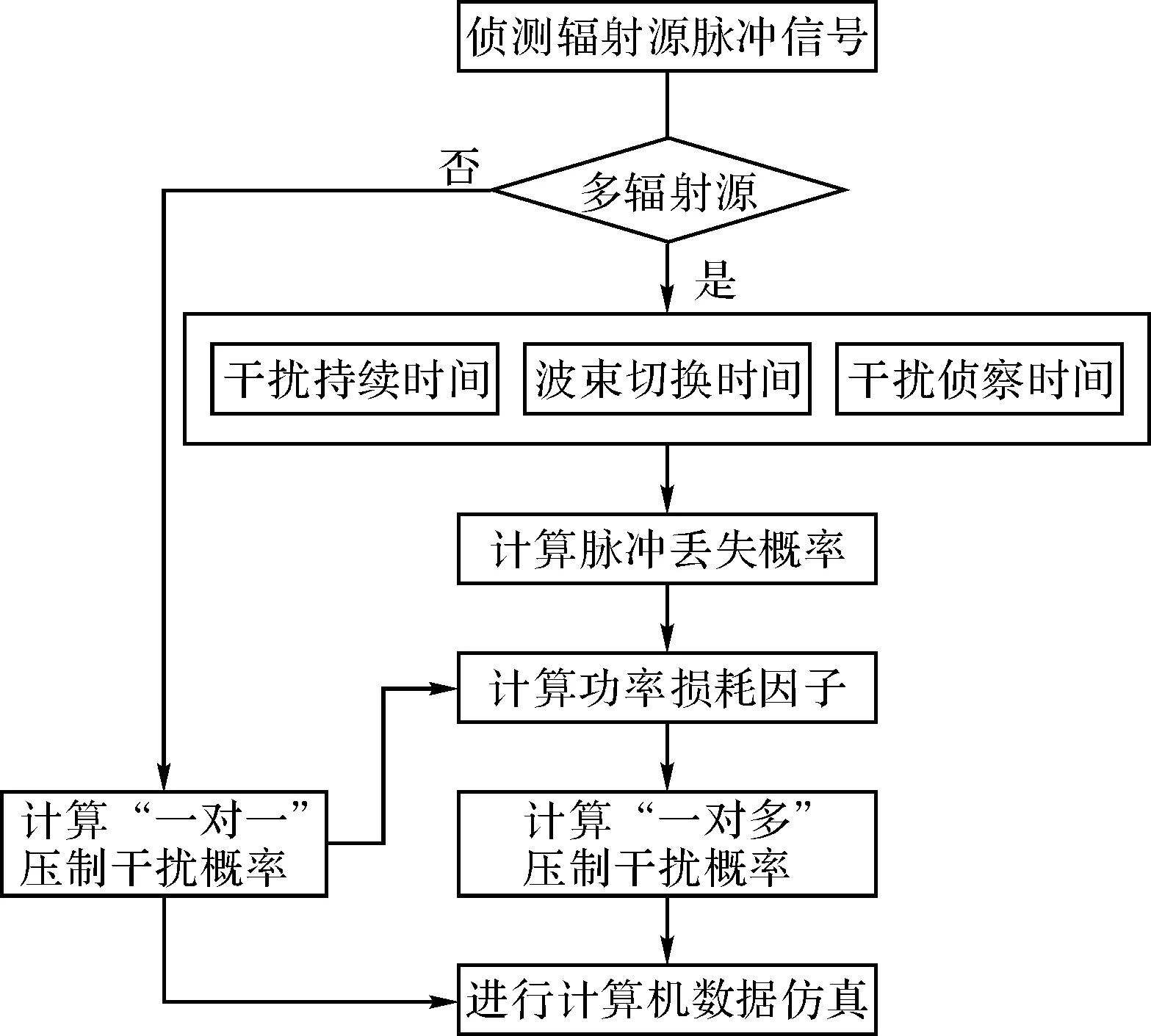
图2 建模仿真流程

4 仿真分析

1) 定量参数赋值

令检测门限y0=27；雷达发射功率*雷达发射天线增益PtGt=20KW；目标的有效反射面积σ=20000m2；干扰机的通频带Δfj=2*雷达接收机的通频带Δfr；雷达扫描扇角φ=90°；雷达功率损耗因子L=6； 干扰机发射功率*干扰机天线主瓣方向上的增益PjGj=120KW； 雷达天线半功率波束宽度θ0.5=1.5°；η=0.8；波束切换时间τ2=4μs；侦察时间τ3=6μs; 干扰时间间隔t2-t1=2000s； 雷达与目标连线和雷达与干扰机连线之间夹角θ(t)=0；干扰机至雷达的距离Rj(t)=被掩护目标至雷达的距离R(t)=300000m,目标速度v=400,干扰机坐标为(xj=30000,yj=30000,0)。

2) 变量参数赋值

令雷达脉冲重复频率fr分别为2000/3000/ 4000/5000；干扰脉冲持续时间τ1分别为20μs、30μs、40μs、50μs。

3) Matlab程序仿真

对多批重频分别为2000/3000/4000/5000、脉冲宽度为5μs,但频率不同、方位不同的雷达进行干扰,当干扰脉冲持续时间τ1分别为20μs、30μs、40μs、50μs时,雷达压制概率和干扰目标批数关系如图3所示。

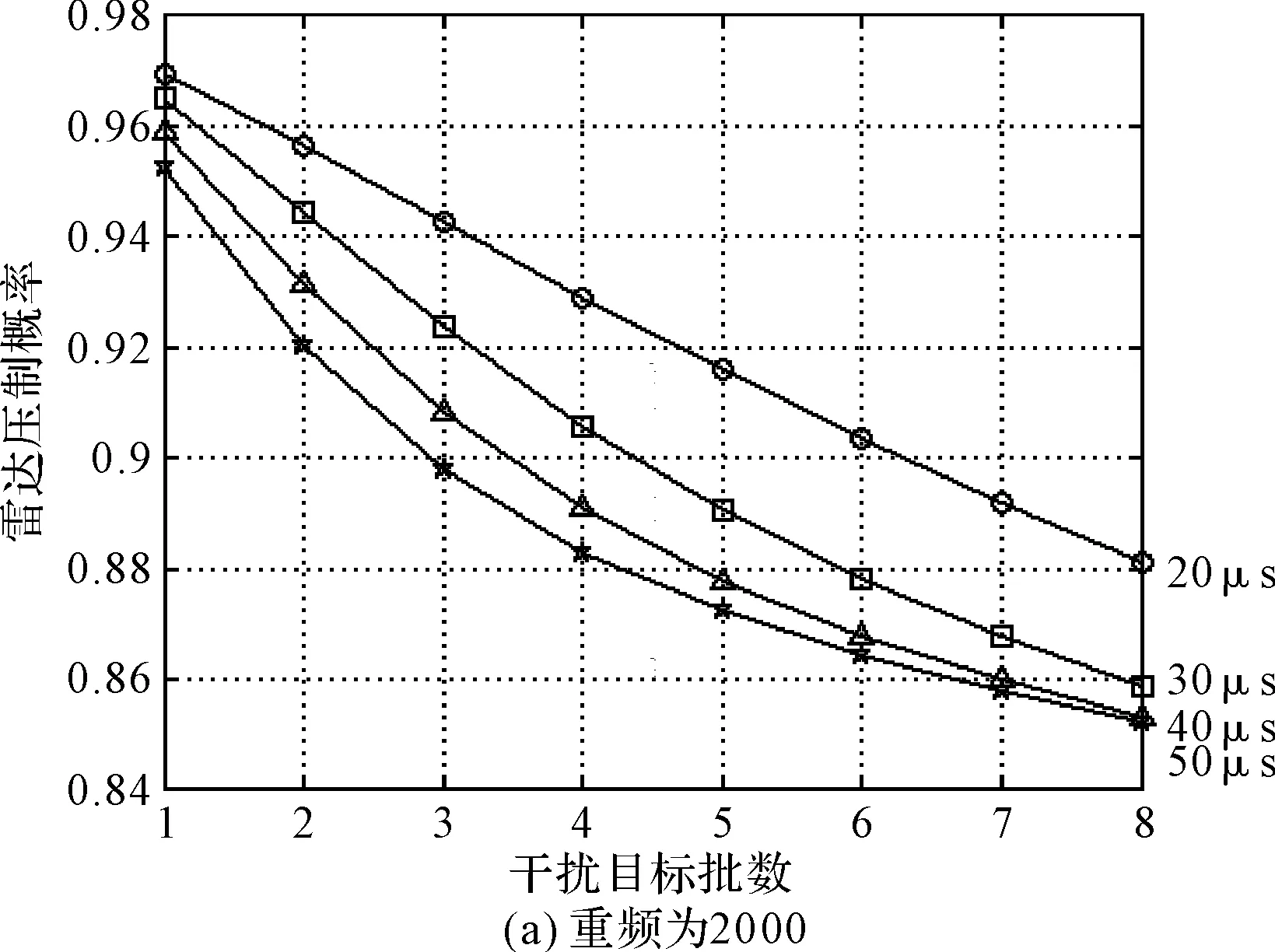
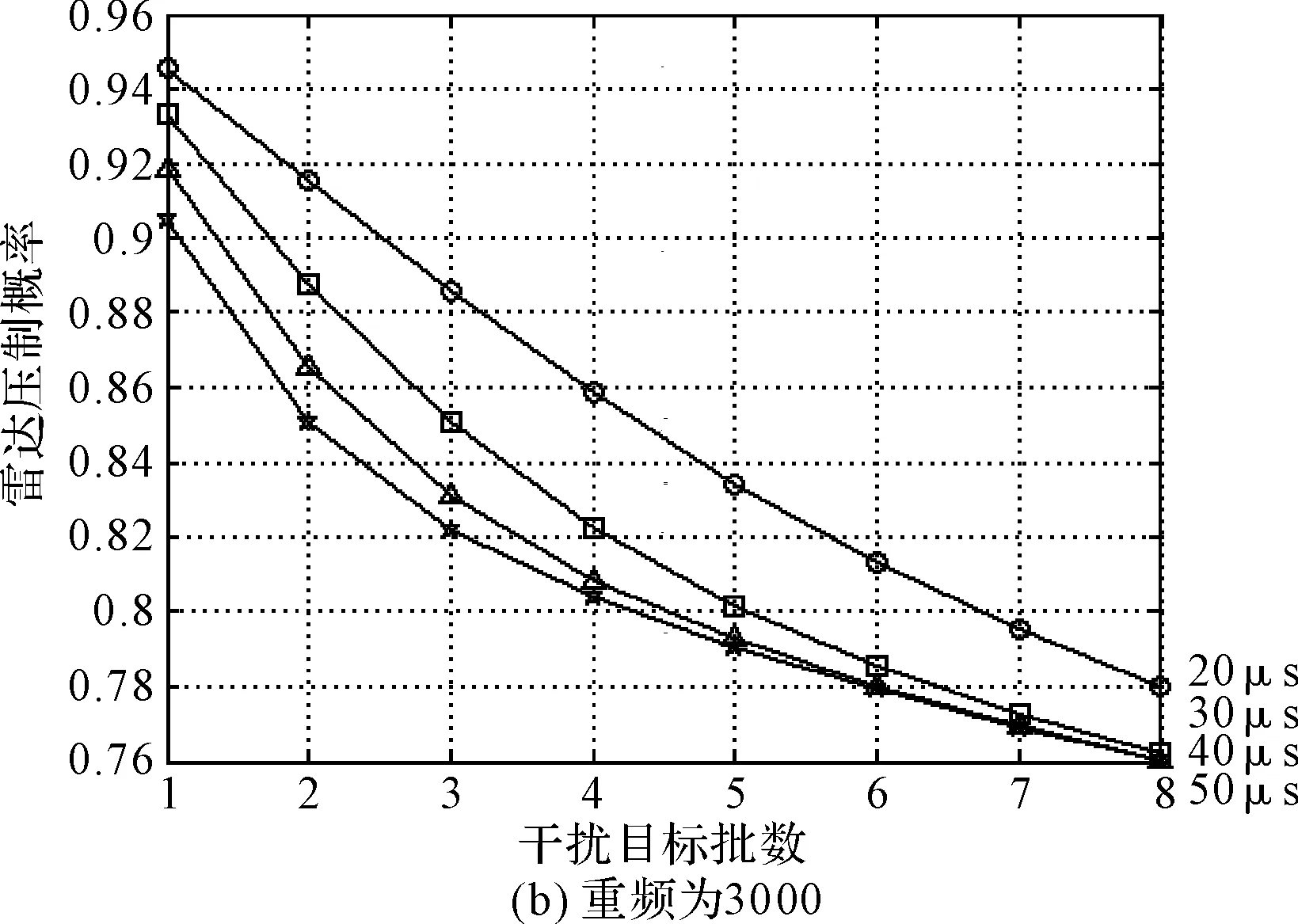
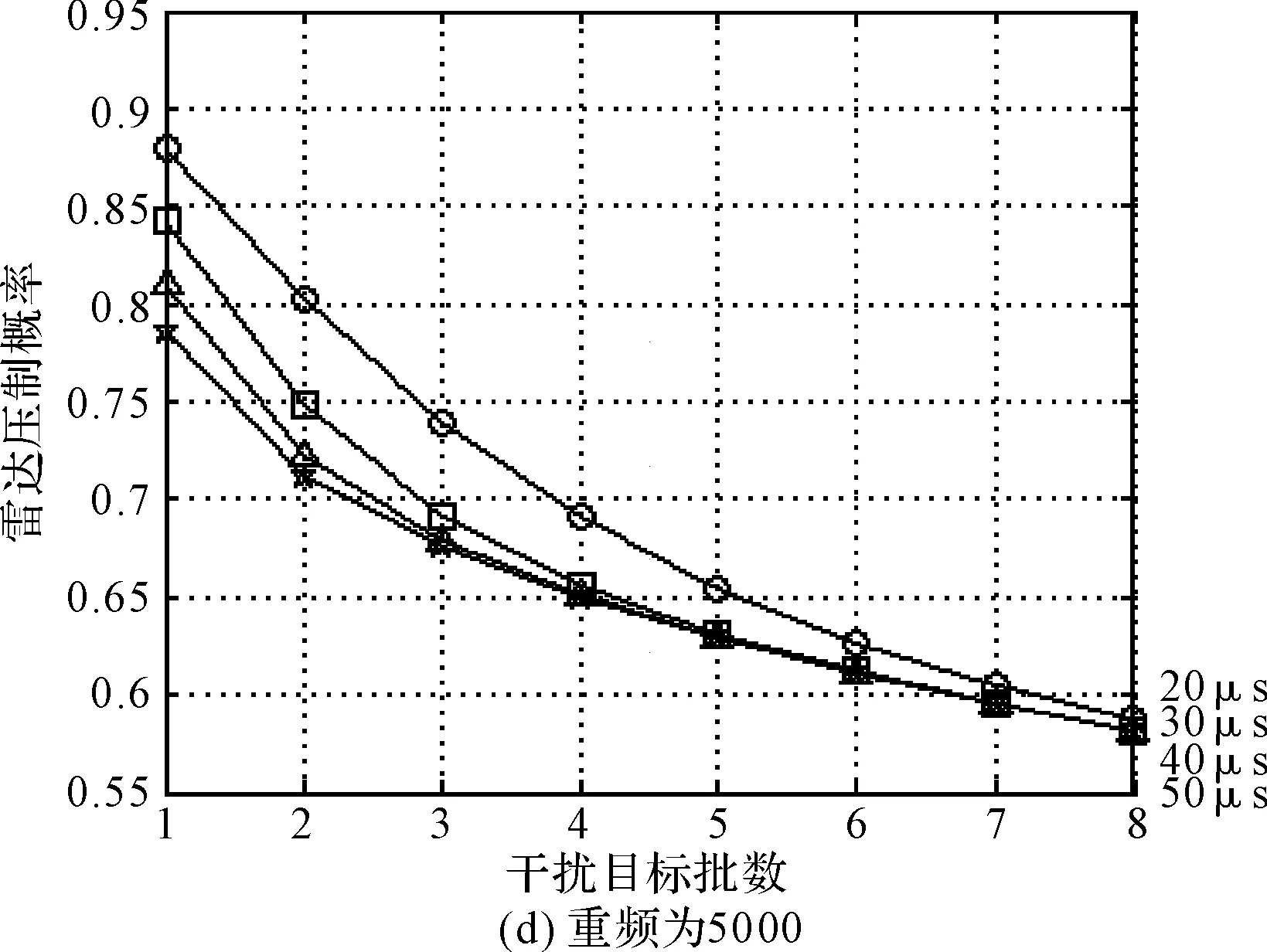
图3 雷达压制概率和干扰目标批数关系

由上图可知,当目标为重频较低的常规辐射源时,即使干扰持续时间延长,干扰机仍可保持对8批目标实现80%以上的干扰成功概率；当目标为重频较高的辐射源时,随着脉冲丢失概率的上升,干扰成功概率下降。当目标重频达到5000时,只能对1批目标实现80%以上的干扰成功概率,干扰效果严重下降。

5 结语

多波束分时压制干扰效果主要受干扰目标重频和干扰脉冲持续时间影响。当干扰机所处电磁环境中平均脉冲密度一定的情况下,受干扰持续时间延长影响,多波束分时压制干扰的多目标干扰批数锐减,压制干扰效果降低；干扰机所处电磁环境中平均脉冲密度越高,干扰成功概率越低。

[1] 孙伯明,梁修华,吴付祥.多波束雷达干扰机作战效能分析[J].舰船电子对抗,2007,30(5):40-42. SUN Boming, LIANG Xiuhua, WU Fuxiang. Operation Effectiveness Analysis of Multi-beam Radar Jammer[J]. Shipboard Electronic Countermeasure,2007,30(5):40-42.

[2] 吕明山,姜宁.多平台雷达有源干扰资源分配算法[J].火力与指挥控制,2013,38(6):55-58. LV Mingshan, JIANG Ning. Research on theRadar ActiveJamming ResourceAssignment Algorithm of Multi- platforms[J]. Fire Control & Command Control,2013,38(6):55-58.

[3] 徐源,王红卫,陈游.多波束干扰系统雷达干扰资源优化分配方法[J].火力与指挥控制,2015,40(5):74-78. XU Yuan, WANG Hongwei, CHEN You. Research on Method of Radar J amming Resource Distribution in Multi- beam J amming Systems[J]. Fire Control & Command Control,2015,40(5):74-78.

[4] 邵国培,曹志耀,刘湘伟.地对空雷达对抗的压制概率和干扰任务分配[J].军事系统工程,1995(4): 15-18. SHAO Guopei, CAO Zhiyao, LV Xiangwei. The Ground-to-air Radar Jamming Probability and Jamming Task Allocation[J]. Military System Engineering,1995(4):15-18.

[5] 王国玉,汪连栋,王国良.雷达电子战系统数学仿真与评估[M].北京:国防工业出版社,2004:120-145. WANG Guoyu, WANG Liandong, WANG Guoliang. Mathematical Simulation and Evaluation of Radar EW System[M].National Defence Industry Press,2004:120-145.

[6] 王红军,王平军,赵宏.噪声干扰对雷达检测概率的影响[J].现代雷达,2003,3(3):4-7. WANG Hongjun, WANG Pingjun, ZHAO Hong. The Influence of Noise Jamming on Radar Detection Probability[J]. Modern Radar,2003,3(3):4-7.

[7] 周怀军,丁士援.噪声干扰条件下雷达检测概率分析[J].舰船电子对抗,2007,30(6):43-45. ZHOU Huaijun, DING Shiyuan. The Analysis of Radar Detection Probability under Noise Jamming[J]. Shipboard Electronic Countermeasure,2007,30(6):43-45.

[8] 杨瑞民,杨景曙,竺小松.一种改进的时分多目标干扰技术原理及实现[J].航天电子对抗,2001(2):41-43. YANG Ruimin, YANG Jingshu, ZHU Xiaosong. An improved Multi-objective Jamming Technology Principle and Implementation[J].Space Electronic Countermeasure,2001(2):41-43.

[9] 李宏,郭雷.单通DRFM干扰机多目标干扰性能分析[J].电子对抗,2011(4):1-4. LI Hong, GUO Lei. The Analysis on Single-pass DRFM Jammer Multi-objective Jamming Performance [J]. Electronic Countermeasure,2011(4):1-4.

[10] 李宏,薛冰,王国玉.干扰机干扰多目标性能分析[J].电子对抗技术,2001,16(1):20-24. LI Hong, XUE Bing, WANG Guoyu. The Analysis on Multi-objective Jamming Performance [J]. Electronic Countermeasure Technology,2001,16(1):20-24.

Multi-beam Time-shift Noise Jamming Modeling and Simulation

RONG Hua CHEN Qiu

(Dalian Navy Academy, Dalian 116018)

The multi-beam time-shift noise jamming can utilize the limited jamming resources on many threaten targets, but it usually causes pulse loss for using time-shift beam switching system which can affect the effect of noise jamming. This paper analyzes causes of pulse loss, builds the multi-beam time-shift noise jamming model. Then the paper simulates the impact of duration of jamming pulse and repetition frequency of radiation source within the complex electromagnetic environment, gives the degree of decline of multi-beam time-shift noise jamming that has reference value to the operational decisions.

multi-beam time-shift noise jamming, duration of pulse, pulse loss, jamming probability

2016年5月17日,

2016年6月20日

戎华，女，博士，教授，博士生导师，研究方向：电子对抗及信息战。陈求，男，硕士研究生，研究方向：电子对抗及信息战。

TP391

10.3969/j.issn.1672-9722.2016.11.005