高中数学中经济类问题分类解析

【摘 要】数学作为一门我们从小就开始打交道的自然学科，常常会对它有一个很大的疑问：它究竟能有多大用处？实际上在经济学的研究和发展当中，数学无疑一直以来都起到了很大的推动作用，很多时候它已经超出了工具的范畴，成为了一种可以融入经济学的思想。在本文中，我以一个高中生的视野，对经济活动中所应用到的高中数学知识进行的分类，并将着重对其中的每一类问题进行重点解析。

【关键词】 高中数学；经济；问题解析

一、数学与经济学的关系

我们在探讨经济数学问题之前要对数学与经济的关系有一个充分的了解。经济学作为一门贯穿历史发展始终的学科，从它诞生到不同的发展阶段，数学都扮演着至关重要的角色。那么，我们可以说正是由于数学的引入，使得原本定性化的经济学变得更加的量化，使得原本抽象的概念经过数学语言的论述显得条理分明。可以说，在经济学当中，数学是经济的肉体，而经济是数学的灵魂。

二、高中数学中的经济类问题分类

对于高中数学知识来讲，经济学当中能够涉及到的有三类：一类是函数问题；一类是在函数的基础之上的导数问题；还有一类就是概率问题。以下就将对这三类问题进行详细讲解与论述。

1.函数当中的线性规划问题

线性规划是运筹学中一个重要的分支，广泛应用到机关、企业、地区及整个国民经济当中，它提供一种数量分析的方法，同时融结几何学有关知识，使解决关于如何安排合理的人力、物力、财力等各种资源的配置来达到最大的收益问题更加自如。

那么下面我就将引入一道关于线性规划问题的典型例题来做具体的分析。

某研究所计划利用神舟七号宇宙飞船进行新产品搭载实验，计划搭载最新产品A、B，该所要根据该产品的研制成本，产品重量，搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如下表：

那么问题就来了：

如何安排这两种产品的件数进行搭载，才能使总预计受益达到最大，最大收益是多少？

本题当中涉及到了诸如研制成本、产品重量、预计收益等一系列的经济因素并且有两个限定的条件，那么如果单纯从经济学的角度来看，我们就需要感性的来思考这些因素之间的关系。

比如，我们要考虑研制成本和成本和最大资金限定额之间的关系，同时还要考虑产品重量与最大搭载限定额之间的关系。

那么我们说，就这道题而言，如果我们采用高中数学知识当中所涉及的线性规划，就可以将这些给定的限制因素紧密的联系在一起，所有的这些经济条件就都会被聚拢，问题也就迎刃而解了。且看解答过程：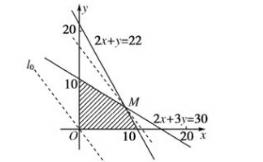

首先将经济因素具体化，我们设搭载A产品x件，搭载B产品y件，预计收益根据数学知识有：z=80x+60y

则，作出可行域，如图：

做出直线L：4x+3y=0并平移，由图像可知，当直线经过M点时，z能够取得最大值，

解得： M（9，4）

所以 zmax=80*9+60*4=960万

最终结果即：搭载A产品9件，B产品4件，可使得总预计受益最大，为960万元。

再回过头来看这个问题，我发现通过高中数学中线性规划的知识来解决这个经济问题，这个经济问题就云开雾散了。所以说，就高中知识而言，线性规划在经济学当中所起到的作用是巨大的，线性规划知识中蕴含的思想与经济学当中讲究优化解决方案的思想有着异曲同工之妙，所以合理的运用线性规划思想在经济学领域里是非常重要的。

2. 关于概率问题

经济学在近些年的发展当中，逐步呈现出了向数学化过度的趋势，而在这其中起到推动作用最大的，无疑就是我们高中所接触过的概率了。近年来，借助于金融学，保险学等经济学分支学科蓬勃的发展，原本作为这些分支学科的辅助工具的概率算法，逐步从幕后走向前台，占据了经济学家重点研究的半壁江山。关于这一点有一个不可否认的事实就是近年来诺贝尔经济学奖的获奖者频频在经济学的随机处理问题上作出过重大贡献的学者。

经济利益当中涉及到的高中数学概率知识有数学期望，方差。我们通过数学期望的计算可以有效地来完成大中型企业当中销售部门对于产品销售问题的分析，借助这一数学工具，企业可以制定相应的参数标准对各类产品进行定价并且有效的预判到他所能带来的收益，达到未卜先知的效用，并且为相关部门作出财务预算起到了至关重要的辅助作用。

下面就引入一道实例为读者进行展示：

大型商场洪福电器商城经过多年的销售调研发现其每个月能够售出的电视台数ζ是一个随机变量，它的分布列如下：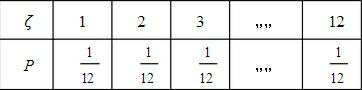

那么洪福电器对于电视机的定价是300元每台，如果电视没有被销售出去的话就要被囤积在仓库作为储备，这样的话每个月公司要为这些囤积的电视机付出100元每台养护费的代价，那么我们的问题是，在每个月的1号需要从厂家购入多少台电视机才能使得自己的月平均收入最大？

命题意图：本题其实正是从概率学的角度来命题，结合概率知识当中关于期望的知识点可以对此题进行有效的解答

具体解法如下：

解：设x为每月1号公司所引入的电视台数，我们只需要思考 1≤x≤12的情况，设洪福电器每月的收益为y元，则y是随机变量的函数，且

y=电器商平均每月收入的平均数，即数学期望为：

3.高中数学知识当中的导数

在西方经济学中，我们不难发现存在着很多关于边际的概念和问题。而对于边际这一经济学中不可忽视的概念来讲，高中数学当中的导数知识恰巧与其不期而遇，碰撞出了鲜亮的火花。

那么导数的定义是：如果一个函数在它所规定的定义域上每一点都可导的话那么就可以建立起这个函数的一个导函数简称为导数。

而边际的含义即为：边际就是说在一个函数当中，因变量对于自变量中每一个单位的改变所能够做出的反应程度。

那么我们在经济学当中所研究的很多问题包括边际效益，边际成本等等都需要导数的介入。

比如说边际成本，我们要研究边际成本，那么必定要求出成本曲线上某一点的导数，因为通过利用成本的增量与生产产品的量变化程度极小时的比值我们才能得出边际成本的具体数值。在这一类问题当中，我们可以知道，导数是非常具有解决问题的价值的。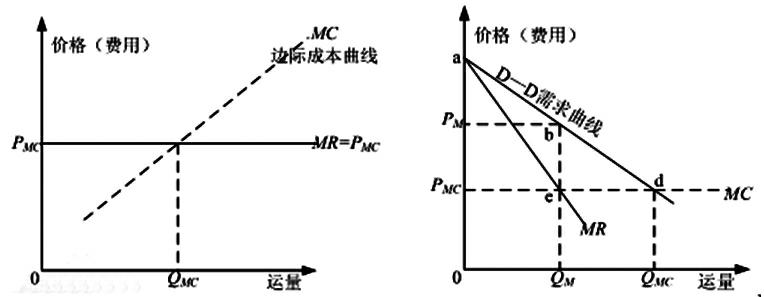

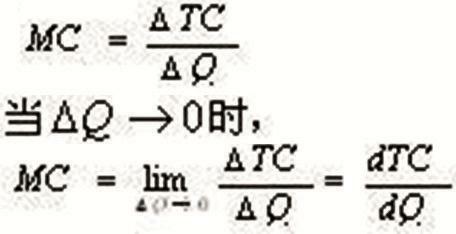
与边际成本有着异曲同工之妙的是边际收益问题。我们说，边际收益是指每增加一个商品的单位销售量所获得的收益增加量。在收益曲线上的某一点，我们可以利用导数中求极限的方法来求出边际收益的具体数值。

三、结束语

高中数学知识实际上已经是我们所受到的教育当中比较高级的部分了，它所包涵的知识广度，深度都是值得探究的。而高中数学中涉及到经济学领域的问题，更是值得我们去探索、发现、深究。实际上经济学是一门非常有规律可循的学科，我们利用数学这一伟大的工具，定可以对经济学问题分析的清晰、透彻、明了。

参考文献：

[1]黄冈兵法.同步学案.高三数学.

[2]难点与方法.数学.

[3]高考中的数学思想——函数与方程 .

[4]数学建模与数学学习的相互促进.

[5]2010年山师大附中模考.

作者简介：

王秋鉴（1999—） ，女，汉族，吉林省吉林市，吉林市第一中学校。