变压器油流继电器动板频繁摆动故障机理分析
范松海,田汉霖,2, 彭智
(1.国网四川省电力公司 电力科学研究院,四川 成都,610072;2.西安交通大学,陕西 西安,710049;3.国网湖南省电力公司 平江县供电分公司,湖南岳阳,414500)
变压器油流继电器动板频繁摆动故障机理分析
范松海1,田汉霖1,2, 彭智3
(1.国网四川省电力公司 电力科学研究院,四川 成都,610072;2.西安交通大学,陕西 西安,710049;3.国网湖南省电力公司 平江县供电分公司,湖南岳阳,414500)
油流继电器动板频繁摆动是电力变压器最常见的故障之一,该故障会导致动板轴承磨损、碎屑浸入油中威胁主绝缘等一系列故障隐患.本文通过建立基于流体力学的仿真模型,分析了变压器油流继电器动板频繁周期性摆动的故障机理及其影响因素,分析结果与现场测试数据吻合.实验结果表明,油流继电器动板的状态主要由油流的状态决定.当油流处在层流状态时,其施加给动板的压力为恒定力,动板在弹簧回复力和流体恒定力作用下保持稳定;当油流处在湍流状态,其施加给动板的压力为非恒定力,在出现卡门涡街时表现为周期性变化压力,继电器动板在流体周期性变化压力的作用下出现周期性摆动现象,其摆动的频率与油流的流量以及联结管结构有关.
变压器;油流继电器;湍流;卡门涡街
油流继电器作为变压器冷却系统的一个辅件,长期处在动作状态,经常由于油管、油泵之间参数设计不合理等导致指针周期性摆动、轴承磨损、频繁动作等各种故障,故障率远高于处于相对静止的变压器本体.据初步统计,全国每年有数千起流油继电器故障,且具有类似的特征:指针频繁摆动导致动板轴承磨损.国网四川省电力公司曾发现9台主变的27只油流继电器相继出现磨损故障,且为同型号同批次的产品.在故障发现前,27只故障油流继电器的指针均出现频繁摆动现象,经过一段时期运行后发现轴套均已严重磨损.
流油继电器动板轴承磨损故障除导致其本身损坏之外,磨损落下的金属粉尘会落入油中并进入变压器主体,对变压器的绝缘性能构成严重威胁.
国内外有很多文献对油流继电器动板频繁摆动故障进行了分析.文献[1-2]认为油流继电器动板摆动的原因归结于过大的油流冲击力.文献[3]仿真分析了不同条件下可压流体流过蝶阀时阀瓣的受力情况,其结构与本文所研究的油流继电器相类似.但文献[3]只是对蝶阀在流体中的静力场做受力分析,没有考虑湍流对蝶阀阀瓣的影响.
本文基于流体力学理论,建立了油流继电器力学模型,通过仿真分析,发现油流状态是流油继电器动板状态的决定因素,而影响油流状态的参数包括油管大小、油流量(油泵扬程)、油流温度(油的动粘滞系数)等,本文的仿真结果与现场实际情况基本吻合.
1 油流继电器的频繁摆动故障
油流继电器是变压器强油风冷却系统内显示油流量变化的装置,常安装在变压器潜油泵的出口处.在继电器联管的侧壁上有一开孔,转轴从开孔中穿过,动板和扭簧固定在转轴上.当变压器潜油泵启动时,继电器联管内产生油流,油流量达到动作流量时,动板在油流的带动下旋转,通过磁耦合使指针同步转动,信号接点接通,发出正常信号.当油流量降低至返回流量时,油流对动板的作用力减小,动板在扭簧扭矩的作用下返回,指针同步旋转,接通故障信号,通知运行、维护人员及时检修,防止变压器油温过高.
如图1所示,油流继电器处在变压器油循环联结管中,其动作状态受弹簧回复力、流油状态等因素控制.当油流处在层流状态时,动板受到油流恒定的压力作用,油流继电器的动板处在静力系中,不会出现频繁摆动现象;当油流处在湍流状态时,油流继电器浸入油中的动板受到油流内部不规则变化的压力作用,呈现不规则频繁摆动现象.当满足一定条件时,绕过动板的油流会出现卡门涡街[4],动板在周期性变化的油流压力作用下出现周期性摆动.

图1 潜油泵和油流继电器结构图Fig.1 The structure of submerged pump and oil-flow relay
2 故障仿真与分析
2.1 力学模型
根据YJ1-150/80型号的油流继电器,建立了其在油流中力学模型.在额定工况下,动板和舵板的形变很小,可以将其视为刚体.在油泵正常工作时,油流量达到动作油流量时,动板受到油流的作用,克服转轴扭簧的扭矩转动到工作位置,此后动板基本不受油流的冲击,可以忽略其受力,而舵板方向基本垂直于油流方向,舵板受到油流的冲击产生转矩,和扭簧扭矩保持平衡,使动作机构保持在工作位置.
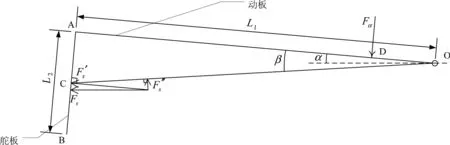
图2 动作机构力学模型图Fig.2 The mechanical model of motion mechanism
机构在油流中的受力情况如图2所示.其中,Fs表示油流对舵板的作用力(包括静压和动压),方向为水平,作用点为AB中点C.Fα表示扭簧在动板上施加的扭力.L1为动板OA的长度,L2为舵板AB的长度.α为动板与水平油流方向之间的夹角,β为O到C点的连线OC与OA间的夹角.
压力Fs在OC垂直方向的分力为:
(1)
油流产生的转矩为:
(2)
扭簧产生的扭力只与α相关,为:
Fα=kα
(3)
式中:k为扭簧弹性系数.
D为扭簧的作用点,OD长度约为OA长度的1/10,扭簧产生的扭矩为:
Tc=Fα×L2/10
(4)
机构受到的合转矩为:
(5)
当机构受力平衡时Ts=Tc,方程式是关于α的超越方程,不能求得关于α的解析解.以YJ1-150/80型继电器为例,L1长为5cm;L2长为0.5cm,则β=arctan(0.5/5)=5.74°.由机构的受力分析易得,只有当时β>α,Fs产生的转矩才为顺时针,动作机构才有可能保持平衡.因此,正常工作时α<5.74°,而在α很小时,式(5)中的sinα可以用πα/180近似,因此式(5)可以简化为:

(6)
可以看出α是关于Fs的函数,当油流是层流时,油流对舵板的作用力Fs在稳定后保持不变,α角也为一定值,油流继电器动板处在静止状态.而油流是湍流状态时,油流对舵板的作用力Fs是时变的,导致α角也随之变化,其摆动频率与湍流涡街频率一致,导致轴套磨损.
2.2 流体力学模型
油流绕经油流继电器动板为不可压缩流动,其定常流可用雷诺时均N-S方程描述.N-S方程能够极大的减少所需的计算量和内存,在工程中普遍应用,其连续方程和动量方程为[5]:
(7)
(8)

根据Boussinesq涡粘性假定,可建立雷诺应力与平均速度梯度的关系.在k-ε双方程湍流模型中,通过引入以下关于湍动能k和湍动耗散率ε的通用输运方程,与式(1)、式(2)构成封闭方程组:
(9)
式中:μt=ρCμk2/ε.式中μt表示湍动粘度,Cμ表示湍动能计算系数,Kφ表示湍动耗散项,φ表示通用湍动变量,k或者ε,σφ表示湍动Prandtl数,Gφ表示湍动生成项.
对于不同的湍流模型,上述各湍动变量对应着不同的求解方法.Launder等人提出的标准k-ε模型,假定μt为各向同性的标量,并给出了模型的相关求解常数[6].适合高雷诺数湍流,但不适合旋流等各向异性较强的流动.Yakhot和Orszag提出的RNGk-ε模型,对标准k-ε模型中μt的各向同性假定做了改进,在湍动粘度中考虑了平均流动的旋转及旋流的影响,在ε方程的原项中,计入了反应主流时均应变率的系数,该模型对强旋流和弯曲壁面流动的计算精度有所提高[7].Realizablek-ε模型,则不再假定湍动能计算式中系数Cμ为常数,将其与应变率建立了联系,从而避免了大时均应变率情况下标准k-ε模型可能导致的负的正应力[8].
本文中所采用的Realizablek-ε模型可以保持雷诺应力与真实湍流一致,在射流计算、旋流计算、带方向压强梯度的边界层计算和分离流计算等问题中,计算结果更符合真实情况.
根据测得的潜油泵出油口尺寸,在Gambit中绘出油流继电器的模型,并进行网格分割.将油流进口定义为压强进口,压强方向与进口边界垂直,并调整压强的大小对应不同流量下的情况.出口定义为压强出口,变压器油箱与油流继电器出口所在水平面的高度差为三米,取密度为850kg/m3、重力加速度为9.8m/s2时,出口压强为24.99kPa,压强方向与出口边界垂直.其它边界均定义为无滑动壁[9].设置时间步长为0.001s,计算时长3s.
2.3 仿真结果
本文利用CFD软件Fluent对油流继电器中的油流状态进行仿真,分析各因素对油流状态的影响,找出湍流的产生条件.本模型采用Realizablek-ε湍流模型计算油流继电器动板和舵板的绕流问题,利用有限体积法求解雷诺平均N-S方程.对流项采用二阶迎风格式,扩散项采用二阶中心差分格式.速度—压力耦合格式为SIMPLEC格式.
模型建立后,可以设置不同的参数进行计算比较,通过Fluent的图形模块绘制出等速线图,及舵板正、反面压强差的变化曲线,并生成视频文件观察不同条件下继电器中的油流状态,观察动板和舵板周围油的波动情况.

经计算,如图3是进口流量80m3/h、油温353K时进口流量的收敛情况,图4是该条件下的速度矢量图.图5是舵板所受压强变化情况.在这种条件下,动作机构后方产生湍流,可以清楚的看到涡街的生成与脱落,动作机构周围油流波动剧烈,机构无法正常工作.
在流体力学理论中,通常使用雷诺数来描述流体的湍流程度,以Re表示:
Re=ρvd/μ
(10)
式中,ρ为流体密度,kg/m3;v为流体流速,m/s;μ为动粘滞系数,Pa·s;d为一特征长度,m.
雷诺数小时,流体中各质点间的粘性力占主要地位,流体各质点平行于管路内壁有规则地流动,呈层流流动状态.雷诺数大时,惯性力占主要地位,流体呈湍流状态.通过计算不同条件,不同雷诺数下的动作机构附近的油流状态,得出在这种动板结构下:Re>2183.6时,尾流处于湍流区;Re<978.1时,尾流处于层流区;978.1 图3 进口流量变化趋势Fig.3 Change trend of inlet’s flow rate 图4 80m3/h,353K下流体等速线图Fig.4 Fluid velocity profile under 80m3/h, 353K 图5 舵板所受压强变化曲线Fig.5 Change curve of pressure on rudder plate 2.4 导致故障的影响因素 (1)油温对油流状态的影响 油温会影响到油流的黏滞性,即其动黏滞系数.油温越高,其动黏滞系数越小,在同样的油流速度下,雷诺数(Re)变大,油流更容易处在湍流状态.不同温度下油流的参数如表1所示. 表1 不同温度下冷却油的密度ρ和动粘滞系数μTable 1 Density (ρ) and viscosity coefficient(μ)of coolant oil under different temperature 当油流流量为80m3/h时,得到不同温度下流体的雷诺数和稳定性如表2所示,舵板压强变化曲线如图6所示,压强波动的频率和幅值与温度的关系如图7所示: 表2 不同温度下流体的雷诺数和稳定性(Q=80m3/h)Table 2 Reynolds number and stability of fluid under different temperature 图6 不同温度下舵板压强的变化曲线Fig.6 Change curve of pressure on rudder plate under different temperature 图7 温度对压强的波动频率和幅值的影响Fig.7 Influence of temperature on oscillation frequency and amplitude 可以看出油温高的情况下,舵板受到的压强波动幅度大,油流不稳定.只有当流体的雷诺数Re<978.1时,油流才处于稳态. (2)流量对油流状态的影响 油流的流量是影响油流状态的重要参数,流量越大,雷诺数越大,流体的惯性力越大,当惯性力的影响大于黏滞力时,油流体处在湍流状态.为研究继电器通过的流量对油流状态的影响,在相同油温条件下,调整不同的进口压强,使进口流量分别达到30m3/h、40m3/h、60m3/h和,80m3/h仿真结果如表3所示,得到的舵板压强变化曲线如图8所示,压强波动的频率和幅值与流量的关系如图9所示. 可以看出流量变化对油流的影响较大.当油流流量小于30m3/h时,油流处在层流状态,油流继电器的动板在油流恒定作用力下保持平衡静止状态;当油流流量大于30m3/h时,油流开始向湍流状态过渡,油流继电器动板在油流周期性变化压力的作用下,出现周期性摆动现象. 表3 不同流量下流体的雷诺数和稳定性(353K)Table 3 Reynolds number and stability of fluid under different flow rate 图8 不同流量下舵板所受压强变化曲线Fig.8 Change curve of pressure on rudder plate under different flow rate 图9 流量对压强的波动频率和幅值的影响Fig.9 Influence of flow rate on oscillation frequency and amplitude (3)联管结构对油流状态的影响 为更加深入探究该型号变压器的故障原因,现对正常工作的某220kV变电站主变BLZ1-150-80/55型油流继电器用相同方法建立模型并进行仿真,将结果与故障变压器的仿真结果进行对比.两种油流继电器的部分参数如表4所示. 表4 油流继电器主要参数Table 4 Main parameters of the oil-flow relays 对两种变压器在油温353K,流量80m3/h的条件下进行仿真,得到流体雷诺数与稳定性如表5所示,舵板压强变化曲线如图10所示. 表5 不同联管下流体的雷诺数和稳定性Table 5 Reynolds number and stability of fluid under different structure of connecting pipe 图10 不同联管结构下舵板压强的变化曲线Fig.10 Change curve of pressure on rudder plate under different structure of connecting pipe 可以看出油流继电器和潜油泵结构,尤其是潜油泵出口大小对油流状态影响较大,在相同流量下,潜油泵出口小,出口油速较高,油流继电器动板附近油流不稳定,油压的波动幅度较大,油流继电器机构随处在湍流状态的流油抖动.而潜油泵出口大,出口油速较低,油压的波动幅度较小,机构不易发生抖动.实际情况与仿真结果吻合程度较高,BLZ1-150-80/55型油流继电器指针稳定,轴套几乎没有磨损,能够长期稳定运行. 为验证所建立的仿真模型,通过高速摄像机实地测量220kV阿海珐SFPSZ-150000/220型变压器的YJ1-150/80型油流继电器(沈阳特种继电器厂,如图11所示)在不同流量以及下油流继电器舵板压强的波动频率,并与仿真结果相比对,结果如图12所示. 图11 YJ1-150/80型油流继电器Fig.11 Oil-flow relay of type YJ1-150/80 图12 舵板压强波动频率随流量变化曲线Fig.12 Change curveof pressure oscillationfrequency on rudder plate under different flow rate 测量不同油温下有油流继电器舵板压强的波动频率,并与仿真结果相对比,结果如图13所示. 图13 舵板压强波动频率随油温变化曲线Fig.13 Change curve of pressure oscillation frequency on rudder plate under different oil temperature 对比可知,仿真计算结果与测量结果吻合较好.对于图11,平均相对误差为6%;对于图12,平均相对误差小于2%.模型计算结果与现场测试基本吻合. 本文基于流体力学理论建立了油流继电器受油流状态控制的仿真模型,仿真分析了油流继电器摆动状态及其影响因素,仿真的结果与现场数据基本吻合.主要结论如下: (1)油流继电器动板的动作状态是弹簧回复力、油流压力共同作用的结果.当油流处在层流状态时,油流压力为恒力,油流继电器处在静力平衡工作状态不会出现频繁摆动现象;当油流处在湍流状态时,油流压力为非恒定力,当油流绕过继电器动板出现卡门涡街时,油流继电器在周期性油流压力作用下出现周期性摆动现象.油流继电器动板的摆动频率与油流作用给动板的压力变化频率基本一致. (2)油流的流动状态受油的温度、流量以及联管结构等各种因素的影响.油的温度越高,油的动粘滞系数越小,流体雷诺数越大,流体内部压力变化频率越大,流体越不稳定.同样,油的流量越大,雷诺数越大,流体内部压力变化频率越大,流体越不稳定.而联管结构会影响到油流进出口流体的速度,进而影响雷诺数和流体状态.联管进出口口径越大,油流速度越慢,雷诺数越小,流体的稳定性越好. [1]王安西,杨田.强油风冷电力变压器油流继电器故障实例分析[J].中国电力,2008,41(10):24-26. [2]贾辉,杨明,冯永刚.强油风冷电力变压器油流继电器故障实例分析[J].吉林电力,2009,39(1):46-47. [3]Leutwyler Z,Dalton C.A CFD study of the flow field,resultant force,and aerodynamic torque on a symmetric disk butterfly valve in a compressible fluid[J].Journal of Pressure Vessel Technology-Transactions of the ASME,2008,130(0213022) :1-10. [4]周光坰,严宗毅,许世雄,等.流体力学[M] .第2版.北京:高等教育出版社,2000. [5]王瑞金,张凯,王刚.Fluent技术与应用实例[M].北京:清华大学出版社,2007. [6]Launder B E,Spalding D B.Lectures in mathematical models of turbulence[M].London:Academic Press,1972. [7]Yakhot V,Orszag S A.Renormalization group analysis of turbulence:basic theory[J].Journal of Scientific Computing,1986,1(1):1-11. [8]Shih T H,Liou W W,Shabbir A,et al.New k-ε eddy viscosity model for high Reynolds number turbulent flows[J].Computers & Fluids,1995,24(3):227~238. [9]于勇,张俊明,姜连田.Fluent入门与进阶教程[M].北京:北京理工大学出版社,2008. Fault analysis for frequent oscillation occurred in movable plate of oil-flow relay on power transformer FAN Songhai1, TIAN Hanlin1,2, PENG Zhi3 (1.State Grid Sichuan Electric Power Company Electric Power Research Institute,Chengdu 610072,China;2.Xi′an Jiaotong University,Xi′an 710049,China;3.State Grid Hunan Electric Power Company Pingjiang County Power Supply Company,Yueyang 414500,China) Frequently oscillation on movable plate of oil-flow relay is one of the most common failure occurred in power transformer. It will cause bearing wearing, metal powder and other hidden troubles which are harmful to insulation. The article analyses the fault reason and influencing factors of frequent, periodic oscillation by building simulation model based on fluid mechanics, occurred in movable plate of oil-flow relay on power transformer. The analysis results are identical with the data obtained from onsite test. The results show that state of oil-flow relay’s movable plate is mainly determined by oil-flow state. When the oil-flow is laminar, the pressure on movable plate is stable, the movable plate keep stable under the restoring force of torsional spring and stable applied force of oil flow. When the oil-flow is turbulent, the pressure on movable plate is unsteady, which is a periodically pressure as the Karman vortex street appears. Movable plate of oil-flow relay has a periodic oscillation under the pressure varied periodically of fluid. The frequency relates to the flow rate and the structure of connecting pipe. transformer; oil-flow relay; turbulence; karman vortex street 1672-7010(2016)02-0063-08 2016-02-28 范松海(1977-),男,四川成都人,博士,高级工程师,从事电气工程输变电设备状态评价研究 TM585 A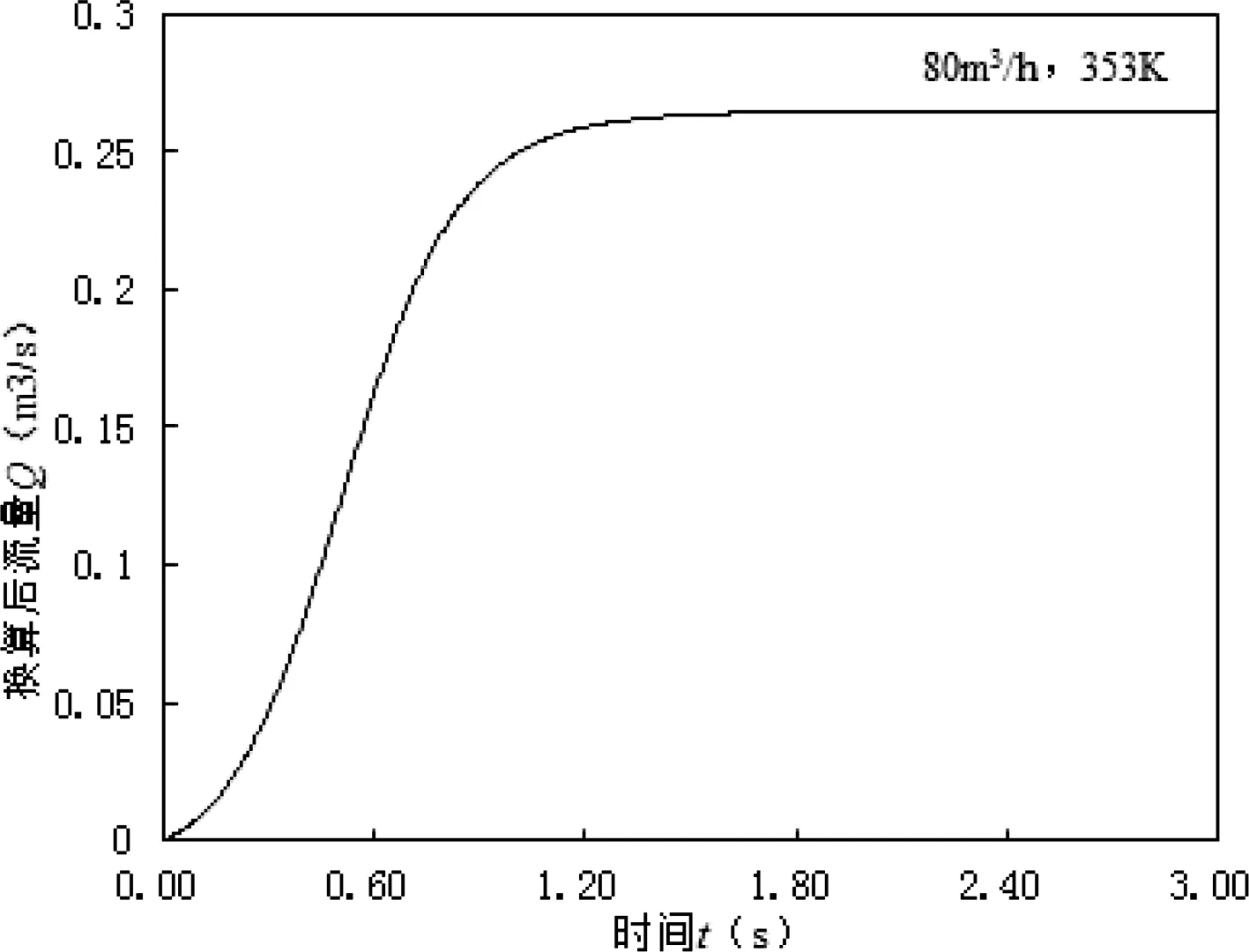












3 现场验证



4 结论

