Shear law of velocity boundary layer

,

(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)



Shear law of velocity boundary layer

LIMingjun,CAIZhenyu

(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

The theory of boundary layer has been known for many years since 1900’s due to Ludwig Prandtl’s contribution. However, solutions to the boundary layer equation does not properly describe high-Reynolds-number flows. In this paper, a generalized Blasius’s equation with fluctuation functionFis derived by using the Prindtl’s boundary equation of mean value and fluctuation, and a shear law of velocity in the inner boundary layer is built theoretically and numerically. The boundary thickness of the leading edge point is found to beδ0=c2/Reu, whereReu=U∞/ν,c=1.7208 as displacement constant orc=0.664 as momentum constant, respectively. Moreover, the Limit Value Theorem on the velocity boundary layer and numerical experiments show that the Newtonian linear shear law of velocity boundary layer is perfectly satisfied forF=0.1 andF=0.01, and the nonlinear shear law is presented forF=0.001 andF→0. Such a mechanism has never been demonstrated in the classical boundary layer theory.

generalized Blasius’s equation; fluctuation function; boundary thickness; Newtonian linear shear law

0 Introduction

A central issue in the study of fluid dynamics is to determine the velocity profile and its valid thickness within a very thin layer in the neighborhood of the solid wall, i.e., the viscous boundary layer theory[1]. In 1904, the concept and basic equations of the laminar boundary layer theory were first formulated by Prandtl[1-2]. Then, this problem was solved numerically by Blasius[3]. If neglecting the stream direction pressure gradient of the Prandtl’s boundary layer equations, one can get the well-known Blasius's equation

(1)

The above equation is an autonomous, third order, nonlinear ordinary differential equation, which results from three similar boundary conditions as follows.

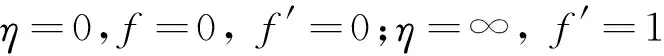
(2)

Conditionsf=0 andf′=0 on the solid wall are “no-slip” boundary conditions, which are fundamental elements in analyzing continuum fluid flow. The analytic evaluation of the Blasius’s equation is quite tedious, sometimes resorts to numerical tools. As Blasius has done, similarity transformation technique play a significant role in most studies in solving the boundary layer problem by transforming a partial differential equation (PDE) into an ordinary differential equation (ODE)[4-5]. However, the simulation of fluid flows with “no-slip” boundaries is plagued with difficulties of rough hydrophobic surfaces, so-called “superhydrophobic” surfaces, and molecular dynamics simulations with consideration of the “slip” conditions[6-8]are usually very time consuming. In 1968, Steinheuer[9]gave a systematic review of the solutions to Blasius's equation.

In the boundary layer, the transition process from laminar to turbulent flow is a basic scientific problem in modern fluid mechanics, and different concepts have been developed to explain the transition mechanism[10]. Among these concepts, streaks and streamwise vorticity are two key features. Some recent works suggested the existence of a self-sustaining process between streamwise vortices and streaks at Reynolds numbers[10-13]. Duriez's study[12]shows that, for Reynolds numberReh=U∞h/v=900(h(h=6 mm)is the cylinder height), the instantaneous velocity field is very fluctuating, and a streamwise modulation exists. He suggested that the self sustaining mechanism through destabilization of the streamwise streaks is probably the reason for the fluctuating at the largest Reynolds numbers where the flow undergoes a transition toward a weakly turbulent state.

As well known, the boundary layer flow takes place mainly parallel to the solid surface, and the inner boundary layer velocity varies rapidly normal to the surface and slowly along the stream direction. Thus the pressure in the boundary layer can be simply assumed as the pressurep(x). Despite all those features, there has not been a deliberate effort to design the structure of the inner boundary layer flow, which interferes with computation progress of fluid flows with solid walls. The present work is aiming for formulating a generalized Blasius's equation within the valid Prandtl's boundary layer by using a generalized similarity transformation and building the shear law of velocity in the inner boundary layer (velocity boundary layer, simply) both theoretically, and numerically.

Let the leading edge of the plate flat be atx=0, the plate be parallel to thex-axis and infinitely long downstream. For simplicity, we here consider a steady flow with the main stream or outer flow velocityU∞, which is parallel to the flat plate. The most widely used boundary layer thickness is simply referred to the distancey=δ(x) from the solid boundary at which the local value of the velocity reaches 0.99 ofU∞. The scale factors foruandyappear quite naturally as the main stream velocityU∞and the boundary layer thicknessδ(x), respectively.

1 Estimation of the boundary thickness of the leading edge point

It is worth noting here that there are two representative thickness formulations, the displacement thicknessδ1and the momentum thicknessδ2in the Prandtl’s boundary layer theory[1]:

(3)

and

(4)

The consistent numerical estimation of the boundary layer has to work out two difficulties. First, the boundary layer approximation of the Blasius’s equation is not valid near the leading edge of the plate (δ>x) because the estimation of Eqs. (3) and (4) are not accurate. Second, according to the definition of the boundary layer thickness, the Prandtl’s boundary layer equations are only valid in the boundary layer satisfying 0≤y≤δwith the following actual boundary conditions

(5)

That is to say, in the inner region of boundary layer, the Prandtl’s boundary layer equations need to be transformed into an appropriate ODE as the Blasius’s equation, which should be dependent on Reynolds number.

In the following, we suppose that the boundary layer thicknessδ(x) is the function of positionx. As well known, one can deal with a singularity similar to the that of moving contact line where the Navier-Stokes equations break down near the stagnation point with a few molecular free pathγ0≈0. Letδ0=δ(γ0) be the boundary thickness of the leading edge point, we will estimateδ0≈1/Reufor largeReuin the following. For each position x in the plate flat, one can get the exact boundary layer thickness as defined by

numerically, wherecis a displacement(or momentum) thickness coefficient,νis the viscous coefficient, a predicted exponent. According to the Prandtl’s boundary layer theory[1], the principle of similarity of the velocity profiles in the boundary layer can be written asu/U∞=φ(y/δ), where the functionφmust be the same for a given distance x from the leading edge. Actually, experience shows that, the velocity is 0 for a suddenly accelerated plate at the stagnation point.

Tab.1 The functionf′(η) for the boundary layer along a flat plate at zero incidence based on Eq.(1).

ηf'Hf'L0.00.00000000.00000000.10.03222100.10050120.20.06444090.20098840.30.09665150.30136560.40.12884010.40160420.50.16098910.50204400.60.19307780.6013393ηf'Hf'L0.70.22507800.70124570.80.25695230.79842810.90.28867210.89313981.00.32019080.99000001.10.3112793︙︙5.00.9915702

Substituting the Blasius’s boundary conditions of Eq. (2) or actual boundary conditions of Eq. (5) into the Blasius’s Eq. (1), we get the values off′, the similar solutions to those of Howarth[4], and both solutions are listed in Table 1. However, there are some physical differences between two solutions. Howwarth’s results show that in the case of Blasius’s boundary conditions (Eq. (2)), in the actual boundaryη=1.0,f′(1.0)=0.320 190 8, it is not consistent with the definition of the Prandtl’s boundary layer thickness. In fact, the boundary conditions of Eq. (2) do not involve the viscosity. This means that the solutions of the Blasius’s equation are independent of the Reynolds number, thus the whole flow pattern in the boundary layer simply undergoes a similarity transformation, longitudinal distances and velocities remaining unchanged. Therefore, it is difficult to investigate the feature of the fluid flow with different Reynolds numbers based on these solutions. In addition, atη=5.0,f′(η)=0.99, which can not be used as the boundary conditions for the outlet flow. Even though we have used actual boundary conditions (5), the Blasius's Eq. (1) is not dependent on Reynolds number and streamline coordination, their solutions are also independent of the Reynolds number. From the view point of fluid dynamics, it is desirable to get a generalized similarity transformation which involves the viscosity.

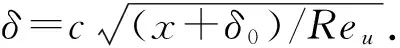
( 6)

wherec=1.720 8isthedisplacementthicknesscoefficientorc=0.664themomentumthicknesscoefficient,respectively.Approximatinglinearly, δ0≈γ0,andformulation(6)isestimatedasthemolecularfreepathnearthestagnationpointfortheflowsoflargeReynoldsnumber.ItiseasytoshowthatiftheunitReynoldsnumberReu→∞,thenδ0→0.Thereforetheclassicalboundarylayerthicknessisjustalimitoftheaboveboundarylayerthickness.

2 The generalized Blasius's equation

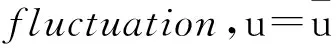
(7a)

(7b)

Using the dimensionless stream functionf(η), the equation of continuity (7a) can be integrated by introducing the following stream function

Thus the velocity components become

(8a)

(8b)

where the prime denoting differentiation with respect toη. Inserting Eqs. (8) into Eq. (6), we have

(9)

In order to obtain the generalized Blasius's equation in the boundary layer, some suitable assumptions are necessary. In order to disclose some relations between the high-Reynolds-number flows and turbulent flow from (9), we take a generalized Blasius's equation as follows

(10)

where fluctuation function

The above equation is derived out with fluctuation, but the third term of the left side includes more physical meaning like surface tension, energy dissipation, et al.. In the case ofF=0, the generalized Blasius's equation is degenerated into the Blasius's Eq. (1). That is to say, the Blasius’s equation can describe inviscid supersonic flow. IfF=+∞, the Navier Stokes equations are degenerated into the reaction-diffusion equations, and the boundary layer becomes the heat diffusion boundary layer.

To check the change of the thickness with different Reynolds number, we plot the numerical value ofδ0,δ(1) andf″ forF=0.1,0.01,0.001 and 0. As shown in Table 2, the decrease of the fluctuation function suggests an increasedf″.

Tab.2 The change of the displacement thickness δ0 and δ(1) with different values of fluctuation function, and the boundary condition f″

In order to analyze the feature of the boundary layer numerically, the generalized Blasius's Eq. (10) is solved with the real boundary conditions. According to the definition of the original boundary layer thickness,η≥1.0 denotes the outlet flow region of the classical boundary layer, thenf′(1)=0.99, and we get the real boundary conditions as

(11)

Fig.1 Shear law of the boundary layer velocity for different values of fluctuation function

We now focus on the velocity profile in the boundary layer with various values of fluctuation function using the new boundary conditions of Eq. (11).

Fig.1 shows the velocity profile of boundary layer. To achieve a clean velocity profile of boundary layer, a coordinates change is used for u/U in x streamline. It is seen that the Newtonian linear shear rate is perfectly satisfied for large values of fluctuation function,F=0.1 and 0.01, and the nonlinear shear law is presented for the smaller value of fluctuation function,F=0.001, or for the Blasius’s equation (corresponding toF=0). In order to show the figure clearly, the values off′ forF=0.1 and 0.01 are substituted byf′(η-0.02) andf′(η-0.01), respectively; the valuesf′ forF=0.001,or Blasius’s equation (corresponding toF=0) are substituted by that off′(η+0.02) andf′(η+0.01), respectively.

To day, it has been well known that a boundary layer flow can switch to turbulence with incresing Reynolds number. According to the Blasius’s work as shown in Fig. 7.7 of [1]and Fig. 2(b) of [15], the velocity distribution is always nonlinear in the boundary layer for higher Reynolds number. The Blasius’s equation is independent with Reynolds number, its numerical results can not explain this feature. Our numerical results show that, with the fluctuation function decreasing, the Newtonian linear shear rate is replaced by the smaller values of fluctuation function, and there is a critical value of fluctuation function where the flow undergoes a transition toward a turbulent state, and to some extent verifying the self sustaining mechanism through destabilization of the streamwise streaks.

明确中国有构建国际商事法庭的必要性之后，在设计国际商事法庭的具体规则之前，我们需要考虑的是中国国际商事法庭的定位问题，或者说是中国国际商事法庭的管辖标准问题。该问题直接决定了中国国际商事法庭如何建设。

3 the Limit Value Theorem on the velocity boundary layer

Moreover, the Limit Value Theorem on the velocity boundary layer[17]can be straightforwardly built. By using the extended domain of definition, 0<η<3, the solution of the generalized Blasius's Eq. (10) can be expended into Taylor’s series as follows

(12)

Based on the boundary conditions of Eq. (10) (for a given Reynolds number,f″(0) is also given by TABLE 2, 0.9

Sinceηwas arbitrarily chosen, the only way in which the above equation can be satisfied for all coefficients to be zero. Then

Combining above values with Eq. (12), we have

Then

Letτ0=10, 0.9

4 Conclusions and summary

In summary, in the solution of generalized Blasius's equations, we have seen that the new boundary equation (5) is more suitable for the computation of flat plate flow. Furthermore, we show that a transition occurs from laminar to turbulent between fluctuation functionF=0.01 andF=0.001. This transition is associated with the separation point and the nonlinear shear law for different values of fluctuation function. Further, the Limit Value Theorem on the velocity boundary layer[17]is built. In conjunction with experimental measurements, the Limit Value Theorem can help to understand the mechanisms of the transition to turbulence.

The present study can be supported by a large amount of classical experiment data published in the literature[13,15-20]. It is noted that Eq. (10) is obtained by the pressure gradient of the main stream. At point of separation,μ(∂2u/∂y2)|y=0=dp/dx, which is in accordance with Eq. (10) of reference[15], letF=τ/Reuwhich decreases with increasingReu. Specially, one can validate the nonlinear shear law in Fig.5 of reference[13]. Recently, Zhou et al. declared that a linear fitting is made toux(z,t) close the plate[18-24], which is opposite with our nonlinear law of boundary layer velocity of higher Reynolds number. In fact, one can find thatux(z,t)is actually nonlinear close the plate in their work (Figs 1(b) of reference[17]), and there exists an extreme value point in the boundary layer.

[1]SCHLICHTING H, GERSTEN K. Boundary Layer Theory[M]. New York: Springer-Verlag, 2004.

[2]YAMAGUCHI H. Engineering fluid mechanics[M]. New York: Springer-Verlag, 2009.

[3]MEIER G E A, SREENIVASAN K R. One hundred years of boundary layer research. IUTAM Symposium[M]. Berlin: Springer-Verlag, 2004.

[4]HOWARTH L. On the solution of the lamilar boundary-layer equations[J]. Proc R Soc London, Ser A, 1951,5:49-62.

[5]SCHROLL R D, JOSSERAND C, ZALESKI S, et al. Impact of a viscous liquid drop[J]. Phys Rev Lett, 2009,104(3):338-346.

[6]SIROVICH L, KARLSSON S. Turbulent drag reduction by passive mechanisms[J]. Nature, 1997,388:753-755.

[7]CIEPLAK M, KOPLIK J, BANAVAR J R. Boundary conditions at a fluid-solid interface[J]. Phys Rev Lett, 2001,86(5):803-806.

[8]CHOI C H, KIM C J. Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface[J]. Phys Rev Lett, 2006,96(6):66001-66100.

[9]STEINHEUER J. Die Losungen der Blasiuss chen Grenzschicht differential gleichung[J]. Proc Wiss Ges, 1968,20:96-125.

[10]WALEFFE F. On a self-sustaining process in shear flows[J]. Phys Fluids, 1997,9(4):883-900.

[11]DURIEZ T, AIDER J L, WESFREID J E. Self-sustaining process through streak generation in a flat-plate boundary layer[J]. Phys Rev Lett, 2009,103(14):144502.

[12]POPE S B. Turbulent Flows[M]. Cambridge: Cambridge University Press, 2000.

[13]VINOD N, GOVINGARAJAN R. Pattern of breakdown of laminar flow into turbulent spots[J]. Phys Rev Lett, 2004,93(11):114501.

[14]SEDOV L I. Continuum mechanics (Chinese, translation from the Russian)[M]. Beijing: Higher Education Press, 2009.

[15]REEUWIJK M V, HARM J J, HANJALIC K. Wind and boundary layers in Rayleigh-Benard convection[J]. Phys Rev E, 2008,77(3):257-260.

[16]REPIK E U. Turbulent to laminar transition of a boundary layer under large negative pressure gradients[J]. J Eng Phys, 1973,24(2):196-200.

[17]ZHOU Q, XIA K Q. Measured instantaneous viscous boundary layer in turbulent Rayleigh-Benard convection[J]. Phys Rev Lett, 2010,104(10):104301.

[18]QIU X L, XIA K Q. Viscous boundary layers at the sidewall of a convection cell[J]. Phys Rev E, 1998,58(1):486-491.

[19]LAM S, SHANG X D, ZHOU S Q, et al. Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh-Benard convection[J]. Phys Rev E, 2002,65(2):066306.

[20]SOLOMON T H, GOLLUB J P. Sheared boundary layers in turbulent Rayleigh-Benard convection[J]. Phys Rev Lett, 1990,64(20):2382-2385.

[21]AITCHISON I J, AO P, THOULESS D J, et al. Effective Lagrangians for BCS superconductors atT=0[J]. Phys Rev Lett B, 1994,51(10):6531-6535.

[22]VERZICCO R, CAMUSSI R. Structure function exponents and probability density function of the velocity difference in turbulence[J]. Phys Fluids, 2002,14(2):906-909.

[23]XU X , BAJAJ K M, AHLERS G. Heat Transport in Turbulent Rayleigh-Benard Convection [J]. Phys Rev Lett, 2000,84(19):4357-4360.

[24]ZHONG J Q, STEVENS R, CLERCX H, et al. Prandtl-, Rayleigh-, and Rossby-Number Dependence of Heat Transport in Turbulent Rotating Rayleigh-Benard Convection[J]. Phys Rev Lett, 2009,102:044502.

1673-5862(2016)04-0419-07

速度边界层剪切定律

李明军, 蔡振宇

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

自20C初,路德维希·普朗特提出相关理论以来,边界层理论被人们所熟知。然而,边界层方程的解并不能恰当地描述高雷诺数流体。通过普朗特边界层方程的平均值和脉动值推导出带有脉动函数F的广义的Blasius方程,并且通过理论推导和数值模拟建立内边界层的速度剪切定律。前缘处边界厚度δ0=c2/Reu,其中Reu=U∞/ν,当求位移厚度时,c=1.720 8,求动量损失厚度时,c=0.664。此外,速度边界层上的极值定理和数值实验表明速度边界层的牛顿线性剪切定律完全满足于F=0.1 和F=0.01,对于非线性剪切定律满足于F=0.001和F→0。这样的机制在传统的边界层理论中从未被讨论过。

广义的Blasius方程; 波动函数; 边界厚度; 牛顿线性剪切定律

计算数学

O242 Document code: A

10.3969/ j.issn.1673-5862.2016.04.008

Received date: 2016-06-20.

Supported: Supported by National Natural Science Foundation of China(11171281).

Biography: LI Mingjun(1968-), male, was born in Yiyang city of Hunan Province,professor of Shenyang Normal University, doctor, doctor supervisor of Xiangtan University.