量子与经典对应:Dirac方程中的速度算符

张治国, 封文江, 郑 伟, 陈 皓, 崔 崧

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)



量子与经典对应:Dirac方程中的速度算符

张治国, 封文江, 郑 伟, 陈 皓, 崔 崧

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

由量子力学中的Bohr对应原理可知,在大量子数情形下,量子力学应过渡到经典力学。在经典极限下,由Heisenberg对应原理可知,厄密算符的量子矩阵元对应经典物理量的Fourier展开系数。利用Heisenberg对应原理研究相对论效应的自由粒子和在匀磁场中的带电粒子的量子经典对应问题。将Heisenberg对应原理应用到相对论领域的Dirac方程,计算出自由粒子的Dirac方程中的α算符及其经典近似,并且研究自旋1/2的带电粒子在匀磁场中的Dirac方程情形。对于相对论效应的自由粒子和在匀磁场中的带电粒子,Dirac理论中的α算符将对应经典的速度。

Heisenberg对应原理; Dirac方程; 速度算符

0 引 言

自量子力学诞生起,人们就开始利用波函数或Schrödinger方程来研究量子与经典的对应问题[1-8]。Bohr原理指出,在大量子数近似下量子力学应过渡到经典力学。在后来的研究中,人们逐渐发现Heisenberg对应原理(HCP)在量子与经典的对应问题的作用[9-15]。HCP以量子矩阵元为基点,认为在经典极限下,量子矩阵元对应于经典物理量的Fourier展开系数。由HCP可知,物理量所有可能的矩阵元之和将给出经典运动方程的解,即在大量子数近似下,有

(1)

式中ψn(x,t)为体系中的波函数,厄密算符F应该对应于一个经典物理方程的解。

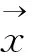
在Hilbert空间中,粒子与反粒子在各自独立的空间里运动,因此应该分别应用HCP来求解Dirac方程的正能解和负能解(对应粒子与反粒子)。本文以正能解波函数研究了相对论领域的Dirac方程里的速度算符,计算表明,在经典近似下,速度算符α对应着经典物理的速度量。

1 Dirac方程

考虑相对论情形下自旋1/2的自由粒子的哈密顿量:

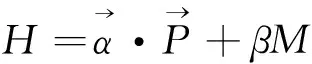
相应Dirac方程:

(2)

式(2)的正能解可写成形式为ψ(x,t)=ψ(x)exp(-iω(t-t0))

(3)

其中:χs为泡利算符σz的本征态(σzχs=sχs),s=±1;V为相空间归一化常数。

由式(2)得:

(4)

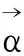
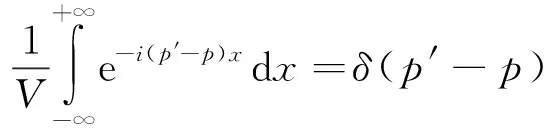
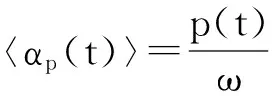
2 磁场中的Dirac方程

相应的Dirac方程为

(5)

假设波函数形式取为

(6)

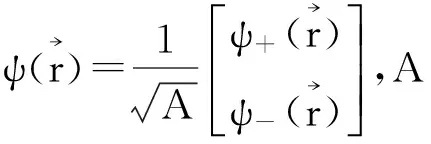
将波函数(6)代入Dirac方程(5),有

(7a)

(7b)

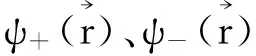
(8)

将式(8)代入第1个方程(7a),得

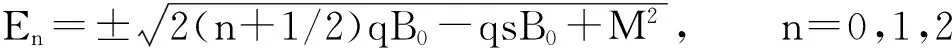
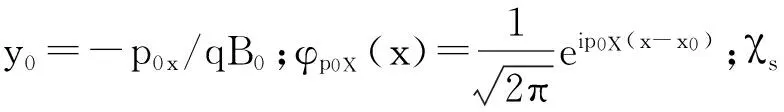
下面计算速度算符的矩阵元。

(9)

(10a)

(10b)

3 经典极限

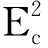
在经典近似下n→∞,(10a),(10b)中αnx(t),αny(t)分别为

(11a)

(11b)

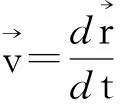
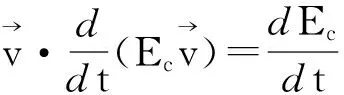
(12)

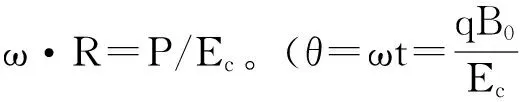
(13a)

(13b)

4 结 论

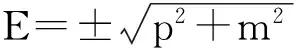
[1]KAYKG.Exactwavefunctionsfromclassicalorbits.II.TheCoulomb,Morse,Rosen-Morse,andEckartsystems[J].PhysRevA, 2002,65:032101.

[2]MAKOWSKI A J, GORSKA K J. Bohr’s correspondence principle: The cases for which it is exact[J]. Phys Rev A, 2002,66:062103.

[3]LUIS A. Classical mechanics and the propagation of the discontinuities of the quantum wave function[J]. Phys Rev A, 2003,67:024102.

[4]LUIS A. Phase-space distributions and the classical component of quantum observables[J]. Phys Rev A, 2003,67:064101.

[5]MAKOWSKI A J. Classical mechanics and the propagation of the discontinuities of the quantum wave function[J]. Phys Rev A, 2002,65:032103.

[6]贾艳伟,刘全慧,彭解华,等. Heisenberg对应原理下氢原子1/r矩阵元的量子-经典对应[J]. 物理学报, 2002,51:201-204.

[7]宋立军,严冬,盖永杰,等. Dicke模型的量子经典对应关系[J]. 物理学报, 2011,020302:1-6.

[8]辛俊丽, 沈俊霞. 谐振子系统的量子-经典轨道、Berry相及Hannay角[J]. 物理学报, 2015,64,240302:1-6.

[9]LIANG M L, ZHANG W Q. Forced time-dependent harmonic oscillator in a static magnetic field: exact quantum and classical solutions[J]. Int J Theore Phys, 2003,42:2881-2884.

[10]GREENBERG W R, KLEIN A. Invariant Tori and Heisenberg matrix mechanics: a new window on the quantum-classical correspondence[J]. Phys Rev Lett, 1995,75:1244-1249.

[11]MOREHEAD J J. Semiclassical integrable matrix elements [J]. Phys Rev A, 1996,53:1285-1289.

[12]LIANG M L, WU H B. Quantum and classical exact solutions of the time-dependent driven generalized harmonic oscillator[J]. Phys Scr, 2003,68:41-44.

[13]李凤敏, 盛朝霞. 海森堡对应原理在含时介观耦合电路中的应用[J]. 量子电子学报, 2006,23(3):408-412.

[14]梁麦林, 张福林, 袁兵. 无穷深势阱中相对论粒子的矩阵元及其经典近似[J]. 物理学报, 2007,56(7):3683-3687.

[15]辛俊丽, 杨悦玲. 中性自旋粒子在二维中心势和均匀磁场中的量子-经典对应[J]. 量子光学, 2012,18(3):246-250.

Quantum and classical correspondence for velocity operator in Dirac equation

ZHANGZhiguo,FENGWenjiang,ZHENGWei,CHENHao,CUISong

(College of Physical Science and Technology, Shenyang Normal University, Shenyang 110034, China)

Due to Bohr correspondence principle in the quantum mechanics, quantum mechanics go to classical mechanics in the case of large quantum number. Based upon Heisenberg correspondence principle, quantum matrix element of a Hermitian operator reduces to the coefficient of Fourier expansion of the corresponding classical quantity in the classical limit. Using Heisenberg correspondence principle, quantum-classical correspondence of the relativistic free particle and the 1/2 spin charged particles in a constant magnetic field are studied. Applying Heisenberg correspondence principle to Dirac equation in relativistic realm, the operator of free particle in the Dirac theory and quantum-classical correspondence are obtained,and 1/2 spin charged particle in a constant magnetic field in Dirac equation is also studied. For the relativistic free particle or the charged particle in a constant magnetic field, the velocity operator in the Dirac theory will reduce to the classical velocity.

Heisenberg correspondence principle；Dirac equation；velocity operator

2016-03-17。

辽宁省教育厅科学研究一般项目(L2014442)。

张治国(1977-),男,辽宁沈阳人,沈阳师范大学讲师,硕士。

1673-5862(2016)04-0441-04

理论与应用研究

O413.1

A

10.3969/ j.issn.1673-5862.2016.04.013