环境污染下具有脉冲扩散的近远海渔业系统连续优化收获问题
吴艳梅, 窦家维, 马 丽
(陕西师范大学 数学与信息科学学院, 陕西 西安 710062)
环境污染下具有脉冲扩散的近远海渔业系统连续优化收获问题
吴艳梅, 窦家维*, 马 丽
(陕西师范大学 数学与信息科学学院, 陕西 西安 710062)
研究了一类在污染环境中具有周期脉冲扩散以及对近海鱼群进行连续收获的近远海渔业系统的动力学行为和优化控制问题.首先,利用脉冲微分方程理论获得了系统正周期解存在性和稳定性的充分条件.其次,在保证系统全局渐近稳定发展的基础上,考虑收获成本因素,以收获努力量函数E=E(t)为控制变量,以一个周期内近海鱼群的经济净收益最大为管理目标,利用脉冲微分系统的极值原理研究控制问题的最优收获策略,获得了最优收获策略的具体表达式及实现条件.
污染环境; 近远海渔业系统; 脉冲扩散; 连续收获; 周期解; 最优收获策略
0 引言与模型描述
近年来, 对于如何有效利用有限的可再生资源的问题受到学术界的广泛关注.众所周知,渔业资源是一种重要的可再生资源,尤其是海洋渔业资源.随着人们生活水平的提高,人类对鱼类的需求量不断增加,这使得对海洋渔业资源的开发需要更加科学有效的管理,目的在于使其在可持续发展的基础上,创造出最优经济效益.关于种群模型的优化开发问题,无论是连续收获,还是脉冲收获都获得了广泛的研究[1-6].近年来,由于沿海工业污染物以及沿海生活污染物的排放导致近海水域生态恶化,渔业资源不断减少,此前建立的关于海洋渔业种群生长的很多数学模型在污染环境中不再适用.文献[7]考虑了环境污染对种群生长的影响,建立了污染环境中单种群连续收获模型:
(1)
受到文献[1]中所建立的海洋渔业扩散模型的启发, 并考虑到实际种群的扩散常常是在很短时间内完成的, 可看成脉冲式的, 在文献[8]中作者建立了连续污染情形下具有脉冲扩散的近远海渔业资源的连续收获模型:
(2)
文献[8]主要研究了模型(2)的动力学行为,并在保证种群可持续发展的条件下,以捕获努力量E为控制变量,以一个周期内对近海鱼群收获量最大为目标,研究获得了最优收获策略.
注意到,在模型(2)中,系统参量及其收获努力量都被限定为常数.但在实际中,由于受到季节性变化及种群的生物异质性等因素的影响,系统参数经常随时间t周期性变化,因此考虑具有周期系数的模型更符合实际.进一步,在考虑优化收获问题时,如果允许收获努力量依赖于时间t,这时由于控制变量E=E(t)的允许范围扩大,可以获得更优的收获策略.考虑这些因素在内,本文研究下面的环境污染条件下近远海脉冲扩散模型:
(3)
在模型(3)中,N1(t)和N2(t)分别表示t时刻同一鱼种群分布在近海和远海的生物量,C0(t)和Ce(t)分别表示t时刻生物体内污染物浓度和环境中污染物浓度.ri(t)(i=1,2)分别表示近海和远海鱼群t时刻的内禀增长率,K(t)表示t时刻近海种群的环境容纳量,E(t)N1(t)项表示对近海鱼群以努力量E(t)进行比例收获.kCe(t)(0 进一步,α、k0、β、θ均为正常数,其中α表示由于种群体内残留毒素而导致内禀增长率线性降低的比例常数;k0βθ表示源自于生物体内污染物的转化率.这里k0=d1/k是每单位质量食物中污染物的转化率,θ是来自于生物资源中污染物的浓度,β是生物体对每单位质量食物的平均摄取率.系统(3)的最后两式表示近海和远海鱼群每隔时间τ进行一次扩散, 假设扩散时间很短,可看成是脉冲扩散,D1、D2为扩散系数,由于近海水域生存环境较差且动物具有趋利避害的本能,本文假设0≤D1≤D2<1. 注意到在文献[8]所研究的模型(2)中要求r2为常量且-r2<0,考虑到环境的周期变化因素,模型(3)中,我们以τ-周期函数r2(t)替代模型(2)中的-r2,并允许r2(t)可以变号.进一步,本文所涉及的系统参量r1(t)>0,K(t)>0为连续可微的τ-周期函数,u(t)>,g(t),m(t),h(t)为τ-周期连续函数,收获努力量E(t)为分段连续的非负τ-周期函数. 本文的主要目的是研究连续污染条件下具有收获的近远海渔业系统的变化规律,进一步确定最优收获策略.在第1节中应用脉冲微分方程理论研究系统(3)正周期解的存在性与稳定性.在第2节,首先应用脉冲微分方程极值原理研究控制问题的奇异收获策略,进一步,结合周期条件及脉冲条件研究了周期脉冲控制问题的最优收获策略.第3节通过一个具体实例,验证了文中主要结论所需的条件,并获得了具体的优化控制策略.第4节总结了全文. 由于系统(3)的第三、四两式独立于N1、N2,因此可将系统(3)分解为下面两个子系统: (4) 及 (5) 首先讨论子系统(4)的解的性质, 并给出下面的引理. 引理1 如果 (6) 证明:直接对系统(4)的第二式在t∈[nτ,(n+1)τ](n∈N)上进行求解, 得到 令Ce((n+1)τ)=Ce(nτ),即可得到 (7) m(σ)]dσ}ds>0. (8) (9) 下文主要研究系统(9)中种群的可持续发展问题, 首先讨论系统(9)具有正初值的解的有界性. 证明:首先当0 显然, 当0 进一步,令V(t)=D2N1(t)+D1N2(t),对于每一个n∈N,当t=nτ时,显然有V(nτ+)≤V(nτ);当t∈(nτ,(n+1)τ]时,则有 其中 当B<1时,直接求解下面方程 (10) 可知(10)有唯一的τ-正周期解, 并且是全局渐近稳定的, 因此(10)的所有正解具有上界.根据微分方程比较定理知,V(t)也具有上界,即存在一个常数Z>0, 使得V(t)≤Z(t∈[0,∞)).因此(9)的所有正解均有界. 下面讨论系统(9)正周期解的存在性.当t∈(nτ,(n+1)τ]时, 直接求解系统(9)的前两个方程得到 (11) 为了表述简便,下文中记 显然有A,F均为正值, 进而可得到 (12) 若记N1(nτ+)=N1n,N2(nτ+)=N2n,结合上式及(9)的脉冲条件即可得到系统(9)的频闪映射为:T=(T1,T2)∶(N1n,N2n)→(N1(n+1),N2(n+1)) (13) 因此, 有关系统(9)的正周期解的存在性与稳定性研究可转化为对映射T的正不动点的相关问题来研究,下面主要研究T的非零不动点的相关性质. (14) 定理2 映射T具有正不动点的充要条件是下面两式成立: 1-(1-D2)B>0, (15) (1-D1)A+(1-D2)B-(1-D1- D2)AB-1>0. (16) 考虑下面函数 f(B)=1-D1-(1-D1-D2)B- B|1-D1-D2|[1-(1-D2)B] = (1-D2)|1-D1-D2|B2- [1-D1-D2+|1-D1-D2|]B+1-D1, 显然, 当1-D1-D2=0时,f(B)=1-D1>0;当1-D1-D2≠0时, 下面分两种情形讨论f(B)的取值情况: (i)当1-D1-D2<0时,f(B)=1-D1-(1-D2)(1-D1-D2)B2,显然,f(B)>1-D1>0; 由上述讨论可知,f(B)>0,即 1-D1-(1-D1-D2)B> B|1-D1-D2|[1-(1-D2)B]≥0, (17) 情形1:1-(1-D2)B<0且(1-D1)A+(1-D2)B-(1-D1-D2)AB-1>0; 情形2:1-(1-D2)B>0且(1-D1)A+(1-D2)B-(1-D1-D2)AB-1≤0; 情形3:1-(1-D2)B<0且(1-D1)A+(1-D2)B-(1-D1-D2)AB-1≤0. (1-D1)A+(1-D2)B-(1-D1-D2)AB-1= [1-D1-(1-D1-D2)B]A-[1-(1-D2)B]≤0, 在(15)式成立的条件下,记 定理3 假设(15)及下面不等式成立: (18) 1-trA0+detA0>0, (19) 1+trA0+detA0>0, (20) 1-|detA0|>0. (21) 下面证明在定理条件下, (19)~(21)成立.首先有 由于trA0>0,如果(19)式成立,则(20)式一定成立,因此只需证明在定理条件下(19)和(21)式成立即可. 首先将trA0,detA0的表达式代入(19)式, 经化简可知(19)式与(18)式等价, 因而(19)式成立. 其次将detA0的表达式代入(21)式,当1-D1-D2=0时,(21)式显然成立;当1-D1-D2≠0时, 在条件(15)下对(21)式进行化简得到 上式等价于: (22) 其中 为了比较R与R1,计算 (23) 由于条件(15)保证了(17)式是成立的, 而由(17)可知,R (b)当x>0时,DT(x)>0; (c)当0 (Ⅱ)如果λ>1, 则有下面(i)或(ii)成立: 首先验证引理2的条件: (a)T(0,0)=(0,0),由于 则 并且对于任意的(N1,N2)>(0,0),有 (b)当(N1,N2)>(0,0)时,DT(N1,N2)>(0,0); 令|μE-DT(0,0)|=0,得到 μ2-[(1-D1)A+(1-D2)B]μ+ (1-D1-D2)AB=0. (24) 由于 Δ=((1-D1)A+(1-D2)B)2- 4(1-D1-D2)AB= [(1-D1)A-(1-D2)B]2+ 4D1D2AB>0, 求解(24)式, 得到DT(0,0)的两个实特征根为: (25) 显然|μ2|≤μ1,因此λ=ρ(DT(0,0))=μ1. 由于条件(18)蕴含着 进一步,可得Δ>[2-(1-D1)A-(1-D2)B]2,其等价于 (26) 结合(25)和(26)得到 (27) 下面分三种情形讨论λ的取值情况: (i)当2-(1-D1)A-(1-D2)B<0时,整理(27)式得到λ>(1-D1)A+(1-D2)B-1>1; (iii)当2-(1-D1)A-(1-D2)B>0时,整理(27)式得到λ>1. 因此,在定理条件下λ=ρ(DT(0,0))>1成立. 由于系统(9)的正周期解的存在性和稳定性等价于算子T的正不动点的相应性质, 综上所述, 关于系统(9)可得到下面结论: 在近远海鱼群保持全局稳定发展的基础上,本部分考虑收获成本因素,研究系统(9)的最优收获策略,目的是使得近海鱼群在一个收获周期内的经济净收益达到最大. 我们将以近海鱼群在一个收获周期内的经济净收益最大为控制目标, 因此定义目标函数为: (28) 其中P,C均为正常数,分别表示近海鱼群的单价及单位收获努力量成本,(N1(t),N2(t))为以E(t)为收获函数时系统(9)所对应的正周期解. 如果存在E*(t)∈E,使得 (29) 2.1 优化系统的奇异控制策略 本小节首先应用脉冲微分系统的极值原理[10,11]求解控制问题(9),(28),(29)的奇异控制策略. 根据[10]中的记号,令 f0=PE(t)N1(t)-CE(t),g0=0 g1=D1(N2(t)-N1(t)), f2=r2(t)N2(t),g2=D2(N1(t)-N2(t)). 若用H表示“连续”Hamilton函数,Hc表示“脉冲”Hamilton函数,则有 H(λ1,λ2,N1,N2,E(t))=E(t)[PN1(t)-C- Hc(λ1,λ2,N1,N2)=D1λ1(τ+)(N2(t)- N1(t))+D2λ2(τ+)(N1(t)-N2(t)). 若记E(t)∈M是优化控制问题的最优收获策略,(N1(t),N2(t))是在该收获策略下系统(9)所对应的最优轨线, 则由文献[10]所给的极值原理([10, 定理1.2])可知,存在协态变量λi=λi(t)(i=1,2)满足下面的协态方程: (30) 并且对每一个t∈[0,τ],最优控制E=E(t)应使得H取最大值.令∂H/∂E=0,即可得到 C-PN1(t)+λ1N1(t)=0. 由上式可得λ1=P-C/N1(t),将其代入(30)的第一式中, 得到 (31) 进一步,将(31)代入(9)的第一式中,解得 (32) 直接求解(9)的第二式, 又可得到 (33) 注意到当条件 (34) 2.2 最优控制策略 下面主要考虑在系统保持全局稳定条件下的优化控制问题,下文中总假设B<1.进一步,由于这里的控制问题是一个周期线性优化控制问题,其最优控制应该是奇异控制与砰砰控制的组合,因此只需确定一个收获周期[0,τ]内的控制策略, 再进行周期延拓即可. (35) 为了满足系统(9)的脉冲条件(36)和周期条件(37): N1(τ+)-N1(τ)=D1(N2(τ)-N1(τ)) N2(τ+)-N2(τ)=D2(N1(τ)-N2(τ)), (36) 与 N1(0+)=N1(τ+),N2(0+)=N2(τ+), (37) 周期结束之前,利用砰砰控制进行调整. 具体地,将(35)代入脉冲条件(36)中,得到 (38) (39) 进一步,由于B<1,故N2(τ) N1(τ+)-N1(τ)=N1(0+)-N1(τ)= N2(τ+)-N2(τ)=N2(0+)-N2(τ)>0. 由上式可知,为了保证N2种群的周期性,在t=τ时刻,N2种群需要从N1种群中得到一定的补充量,与此同时N1种群则要减少同等生物量以补充N2种群.为了使得种群N1在输出给N2种群部分量的条件下仍能保证其周期性,则需要利用砰砰控制,即对N1种群在t=τ之前停止收获一段时间(应用E=0进行收获),假设停止收获的时刻为t=t1,t1应由下式确定: (40) 其中 最后,收获控制策略应取为 (41) 我们注意到当(34)成立时, 又由于 从而 (42) 结合(34),(42)及系统(9)的周期性,可知 为了保证上面的最优控制策略(41)能够实现,则需要由(40)式确定的t1满足0 定理6 假设B<1以及(34)式成立,如果有 (43) 成立,则优化收获策略(41)可以实现. (44) (45) 考虑下面的连续收获系统τ=1: (46) 取目标函数为 (47) 首先由于引理1的条件: 满足,因此下面系统 0.01sin(2πt), =1.170 8. 故定理6的条件满足,则由定理6可知,存在t1=0.7∈(0,1),使得目标函数(47)在一个收获周期[0,1]内的最优收获策略为: (48) 这里 下面验证在策略(48)下, 种群N1,N2是全局渐近稳定的.首先,B<1保证了(15)是成立的,又计算得到R=0.646 4,进一步 即(18)式成立.又由于(18)式与(16)等价,从而定理5条件满足,因此在以E=E(t)为收获策略时种群N1,N2是全局渐近稳定的. [1] Clark C W.Mathematical bioeconomics:The optimal management of renewable resources[M].2nd edition. New York:John Wiley and Sons,1976. [2] Xiao Yanni,Chen Lansun.Optimal impulsive control in periodic ecosystem[J].Systems Control Lett.,2006,55(7):558-565. [3] Kang Baolin,Liu Bing,Xu Ling.Dynamics of an inshore-offshore fishery model with impulsive pollutant input in inshore area[J].Nonlinear Dyn.,2012,67(4):2 253-2 362. [4] 黄灿云,李雨佳.局部区域保护下生物资源的最优脉冲收获策略[J].兰州理工大学学报,2014,40(5):140-144. [5] Dong Lingzhen,Chen Lansun,Sun Lihua.Optimal harvesting policy for inshore-offshore fishery model with impulsive diffusion[J].Acta Mathematica Scientia,2007,27B(2):405-412. [6] Zhao Zhong,Zhang Xuiquan,Chen Lansun.The effect of pulsed harvesting policy on the inshore-offshore fishery model with impulsive diffusion[J].Nonlinear Dyn.,2011,63(4):537-545. [7] Liu Bing,Chen Lansun,Zhang Yujuan.The effects of toxicant input on a polluted environment[J].Journal of Biological Systems,2003,11(3):265-274. [8] Kang Baolin,Liu Bing,Ma Yi.Dynamics of inshore-offshore fishery concerning optimal harvesting policy in a polluted environment[J].Journal of Biomathematics,2010,25(4):583-592. [9] Smith H L.Cooperative systems of differential equations with concave nonlinearities[J].Nonlinear Analysis,1986,10(10):1 037-1 052. [10] Blaquiere A.Differential games with piece-wise continuous trajectories[J].Lecture Notes in Control and Information Science,1977,3:34-69. [11] Rempala R,Zabczyk J.On the maximum principle for deterministic impulse control problems[J].Journal of Optimization Theory and Applications,1988,59(2):281-288. 【责任编辑:陈 佳】 Optimal harvesting problem for a class of inshore-offshore fishery system with impulsive diffusion in a polluted environment WU Yan-mei, DOU Jia-wei*, MA Li (School of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710062, China) In this paper,the dynamic behavior and optimal control problem for a class of inshore-offshore fishery system with periodic impulsive diffusion and continuous harvesting in a polluted environment is studied.Firstly,the sufficient conditions for existence and stability of the positive periodic solution are investigated by using impulsive differential equation theory.Moreover,under the condition ensuring that the system is globally asymptotically stable,a related optimal control problem is investigated by applying the maximum principle of impulsive differential systems,the purpose is to control the harvesting effort to maximize the inshore subpopulation′s harvesting profit which is the difference between economic revenue and cost.The exact expression and realization condition of the optimal harvesting policy are given explicitly. polluted environment; inshore-offshore fishery system; impulsive diffusion; continuous harvesting; periodic solution; optimal harvesting policy 2016-08-22 国家自然科学基金项目(61272435) 吴艳梅(1991-),女,山西吕梁人,在读硕士研究生,研究方向:脉冲微分方程理论及应用通讯作者:窦家维(1963-),女,陕西西安人,副教授,博士,研究方向:脉冲微分方程理论及应用,jiawei@snnu.edu.cn 1000-5811(2016)06-0187-10 O175.1 A1 系统正周期解的存在性及稳定性
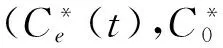

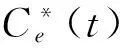

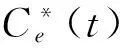



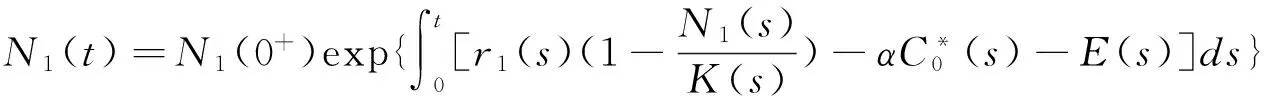
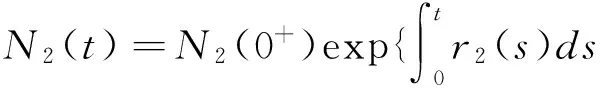

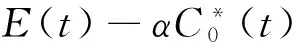

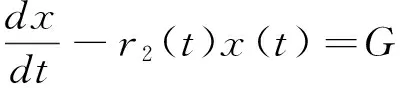























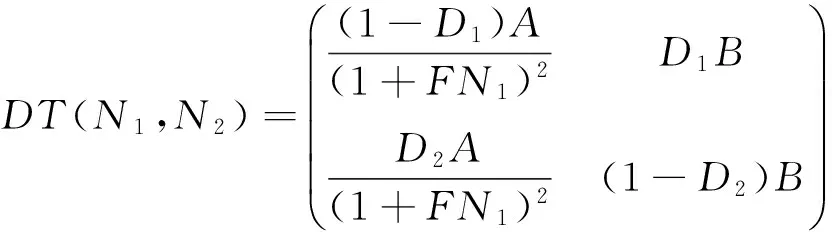









2 优化控制策略









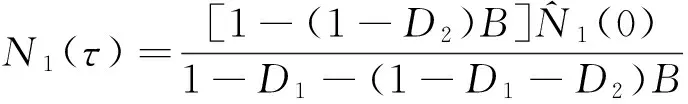
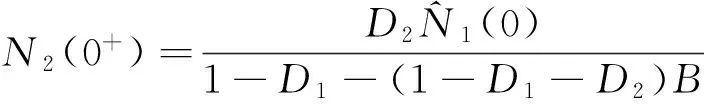



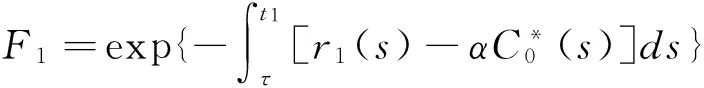

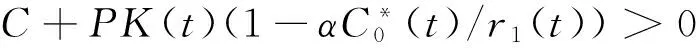












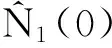
3 应用举例

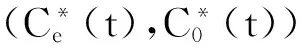
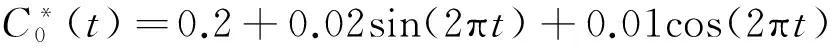
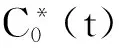

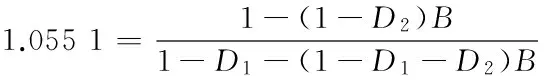


4 结论


