力场与时间有关系统的功能定理及其应用
朱如曾
(中国科学院 力学研究所 非线性国家重点实验室(LNM)微重力国家实验室(NML),北京 100190)
教学研究
力场与时间有关系统的功能定理及其应用
朱如曾
(中国科学院 力学研究所 非线性国家重点实验室(LNM)微重力国家实验室(NML),北京 100190)
与时间有关的有势力场与其他力共同作用系统的功能定理具有比普通的功能定理更为强大的应用价值,本文介绍这一功能定理,并应用于不同参考系观察同一系统的机械能如何变化的两个简单实例:在地面上和升降机中观察地面附近同一质点的机械能变化,在地面上和在运动车厢里看一端固定于车厢壁的弹簧振子的机械能变化.指出了有些文献的有关错误.
与时间有关力场;功能定理;机械能守恒定理;重力场;轻质弹簧振子
如所熟知,与时间无关的有势力场中力学系统的功能定理十分重要,按照功能定理,系统机械能的增加等于其他力所做功之和.功能原理在许多领域的应用研究一直连绵不断,且越来越广泛深入[1-3],甚至应用于当前盛行的分子动力学模拟,如纳米液滴的碰撞模拟研究[1]、生物医学中对疾病的表征方法研究,如脑瘫儿童步态病理的标定研究等等[2].对于既存在其他力,而有势力场又与时间有关的系统,机械能的变化自然应当由一种更为广泛的功能定理所决定[4,5].这种功能定理无疑是十分重要的基本定理,而且必将有广泛的应用前景,但是不属于现行大学物理课程的范围.然而在大学物理教学中与时间有关力场的例子往往又不可避免,对于这样的例子,机械能的变化往往只能单一地从动力学的计算得出.对物理教学讨论文献中出现的这类典型系统的机械能变化问题,在动力学计算方法之外采用与时间有关力场中的功能定理进行处理既方便,对于澄清物理概念又大有好处,所以本文将在第一节介绍这一功能定理,然后在第2节将其应用于不同参考系观察同一系统的机械能如何变化的二个简单实例:在地面附近重力场中的质点和一端固定在车厢壁的轻质弹簧振子,最后第3节是结论.
1 力场与时间有关系统的功能定理及机械能守恒定律
定理1 力场与时间有关系统的功能定理
对任一惯性系中各质点的位置和速度分别为ri和vi(i=1,…,n)的 n质点系统,如果除受到与时间t有关的,势函数分别为 Epin和 Epout的有势内力fini和有势外力 fouti的作用外,还受到其他力 fothi(i=1,…,n)的作用,则系统的机械能E的变化率为

式中,E=Ek+Ep,Ep=Epin+Epout,Ek是系统的总动能.
证明 由势函数的定义
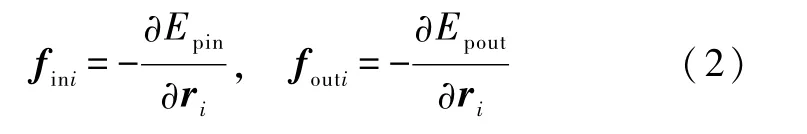
得
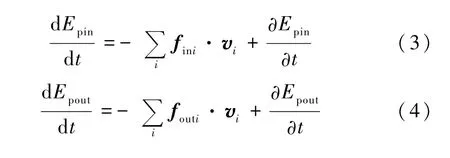
系统的总动能Ek遵从动能定理

将式(3)、(4)和式(5)相加即得式(1).证毕.
需要注意,实际的内力势函数都不显含时间,除非特殊假定.式(1)等价于文献[6]中用广义坐标表示的“机械能变化规律”.式(1)曾见于文献[4],在单质点一维运动且无其他力情况下式(1)简化为文献[5]的结果.
当参考系不是惯性系时,只需将惯性力视为其他力,就可以适用本功能定理.
当势函数与时间无关时,式(1)右边第二项恒等于零,本功能定理即退化为势函数与时间无关的普通的功能定理.
由功能定理直接得到机械能守恒定律[4].
定理2 力场与时间有关系统的机械能守恒定理
对于力场与时间有关的系统,如果在某段时间内
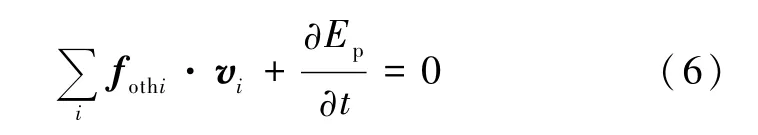
则在该段时间内系统的机械能守恒.
上述功能定理和机械守恒定理的证明并未限定于哪一个具体的惯性系,所以这些定理对各惯性系都成立,这符合相对性原理的要求.由于非惯性系的表征(加速度和角速度)是惯性系的观察量,因此“将惯性力视为其他力的非惯性系,可适用上述功能定理和机械能守恒定理”就是惯性系的一条定理,它当然也必须服从相对性原理.但是对于同一系统,相对性原理显然不能也没有义务保证条件(6)对所有惯性系(和用惯性力修饰过的非惯性系,下同)一致地满足或一致地不满足,所以相对性原理虽然保证机械能守恒定理对于所有惯性系成立,但是它不能保证机械能守恒的事实对于所有惯性系都成立.
2 应用实例
2.1在地面上和升降机中观察地面附近同一质点的机械能变化
如图1所示,一质量为m的质点在地面附近重力场作用下相对于地面运动,一电梯相对于地面以恒速v0上升.现在分别从地面参照系A和电梯参照系B中看,质点的机械能是否守恒?
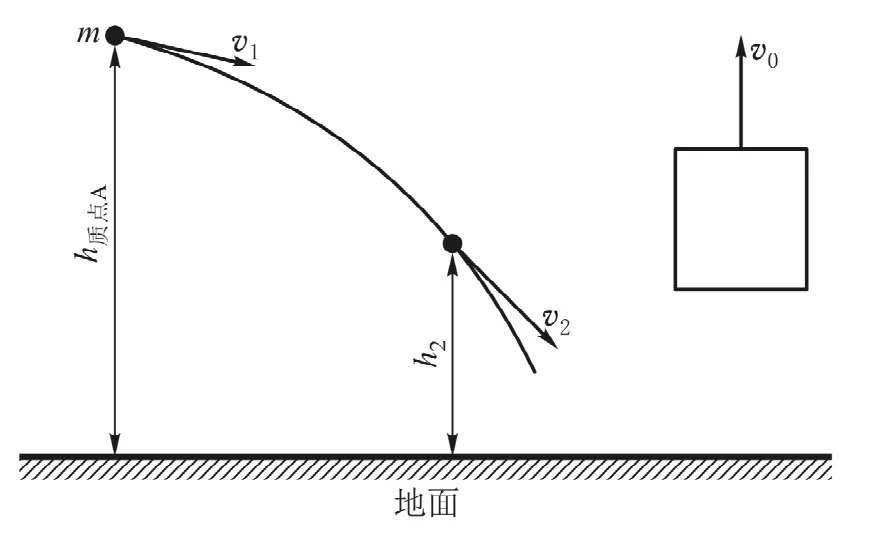
图1
对于这一问题,忽略地球的自转和公转、地球上其他物体相对于地球的运动和其他天体的影响,假设只有地球、质点和电梯这3个物体存在,而电梯对质点的引力可以忽略.对于这一假设的模型,由于质点与地球之间的相互吸引,在质点与地球的共同质心系(惯性系)中看,地球和相对于地球做匀速运动的电梯都有微小的加速度mg/M(M是地球的质量,g是重力加速度,在地面附近视为常数),因而都不是严格的惯性系.因此在地面系和电梯系中看,质点和地球都受到微小惯性力的作用.质点受到的惯性力(-m2g/M)与地球对它的引力mg相比显然可以忽略不计;地球受到的惯性力是(-mg),在地面系中看,地球速度为零,惯性力不做功;但是在电梯系中看,地球有速度(-v0),故惯性力对地球所作功率是mgv0,这是不能忽略的[7].细心的读者自然会问,其他被忽略的因素对地球的实际小扰动可能比质点对地球引起的小扰动大,这种模型是否不合理啊?实际上,假设被忽略的其他因素和质点实际上分别使地球得到了远小于g的加速度a1和a,从而使电梯中的惯性力对地球做的功率为a·Mv0+a1·Mv0.同时,其他因素提供的外力本身对地球所做的功率是-a·Mv0,它抵消了对应的惯性力的功率项.所以对于本问题,计算一个质点的机械能变化时,不必考虑真实存在的其他可能大得多的对地球的小扰动.
当我们把地球和质点作为一个两体系统讨论时,重力场称为它们之间的相互作用内力场.如果在我们所采用的某参考系中,能够预先知道或近似知道地球的坐标(即地面的坐标)随时间的变化(例如,在地面系 A中 h地面A不随时间而变,在电梯系 B中h地面B=h地面B(0)-v0t,在地球和质点的共同质心系C中 h地面C近似不随时间而变),这个地球的坐标就可以不作为未知位形变量进入系统的运动微分方程之中,于是我们面对的是单质点在重力场中的运动,此时重力场便被称为由地球坐标的时间函数所确定的已知外力场,它是来自内力场的外力场.因此得到如下定义[8]:
定义1 在外力场概念下质点的重力势能就是内力场概念下质点与地球之间的相互作用势能.
我们知道,内力势能由系统中各对质点之间的距离决定,而与系统中各质点的速度无关.由于参考系(惯性系和非惯性系)的变换完全不改变系统中各对质点之间的距离以及相互作用力,所以内力势能具有参考系变换下的不变性(即在不同参考系同时观察同一系统的内力势能是相等的),于是由定义1得到定理3:
定理3 对同一系统,不同参考系中的势能(内力势能及根源于内力场的外力势能)具有参考系变换的不变性.
为简单起见,做如下关于势能零值的约定:
约定1 质点与地面距离为零时质点与地球之间的相互作用势能即重力势能为零.
(为了进一步认识势能数值在地面和升降机中相等这一关键概念,可以以公共的无限远处为势能零点,分别在地面系和升降机中对地球引力进行精确的等时积分.由于引力和距离都是参考系变换不变量,因此引力的等时积分即势能也是参考系变换不变量.当然,为了在升降机中讨论质点的运动规律,可以以升降机的底为势能的零点.这样用牛顿力学算出的任何结果在升降机中都正确.但是要涉及参考系变换就必须遵从本文定义1和定理3,否则势能便不可比较.这就像世界各国在涉及外贸时必须换为世界货币才能比较大小和交换!).
下面对图1所示系统分别采用内力场和外力场概念进行处理.
2.1.1内力场处理
既然视为内力场,地球与质点便被视为是两体系统,地面和质点在参考系A和B中的竖直坐标h地面A,h质点A,h地面B和 h质点B以及水平坐标就都是系统的位形坐标.
1)从地面上看(非惯性参考系A)
按照约定1,当(h质点A-h地面A)=0时的相互作用势能EpinA为零.对式(2)的第一式做等时积分并利用约定1得
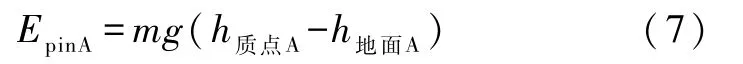
此式表明 EpinA只显含位形坐标 h质点A和 h地面A,而不显含时间.系统虽然受到属于“其他力”的惯性力作用,但是由于在A中看地球静止(h地面A为常量),惯性力不作功,而惯性力对质点所作的功又可以忽略不计,所以功能定理式(1)给出两体系统的机械能EA满足

其中
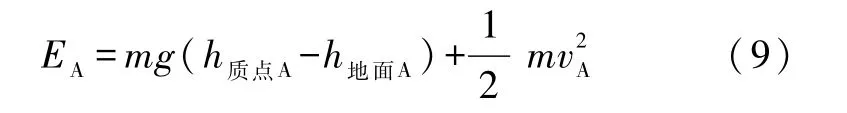
(vA为质点的速度,地球动能始终保持为零).式(8)表明两体系统机械能(近似)守恒.
2)在电梯参照系(非惯性参考系B)中看
由定理3和非惯性系A中的内力势能式(7)得参考系B中的相互作用势能为
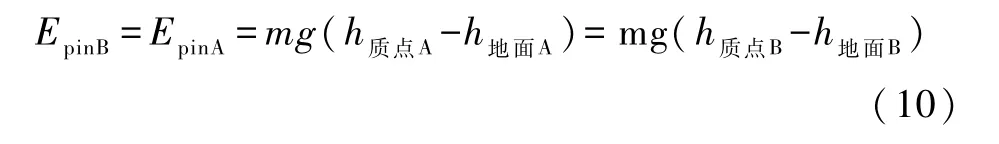
(等时积分势能函数的定义式(2)的第一式,并利用约定1也能给出此式.)式(10)表明,相互作用势能只显含二个位形坐标 h质点B和 h地面B,而与时间无关.作为其他力的惯性力-mg对质点所作的功可以忽略不计,但对地球所作功率为 mgv0,所以功能定理式(1)给出两体系统机械能EB(近似)满足

其中
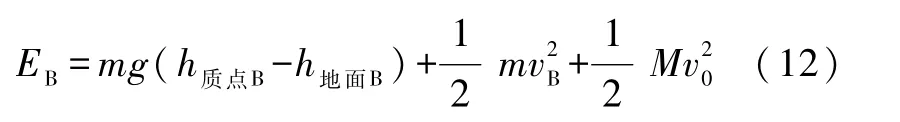
这里vB为质点的速度,且
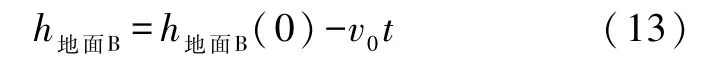
(将式(12)代入式(11)左端并利用式(8)可验证式(11)).式(11)表明在电梯参照系中看,系统的机械能不守恒,并表明其根源在于惯性力对地球所做之功不能忽略.这也就是文献[8]的结果.
2.1.2外力场处理
此时,地球的竖直坐标 h地面A和 h地面B以及水平坐标都是时间的已知函数,不作为待求的位形坐标.因此系统成为重力场中的单体系统,其位形坐标就只有质点的竖直坐标 h质点A和 h质点B及其水平坐标.
1)在地面上(非惯性参考系A)看.直接利用定义1和式(7)(或者对势能函数的定义式(2)的第二式等时积分,并利用约定1)得A中的重力势能为

式中,h地面A与时间无关,此式表明势能只显含作为位形坐标的质点的竖直坐标而不显含时间.质点所受作为其他力的惯性力所作之功可以忽略不计,所以功能定理式(1)给出机械能EA满足

其中
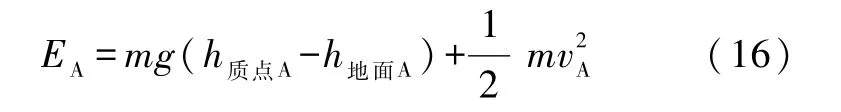
式(15)表明系统机械能(近似)守恒,这与内力场处理的结论(8)一致.
2)从电梯(非惯性参照系 B)中看.地面的坐标为
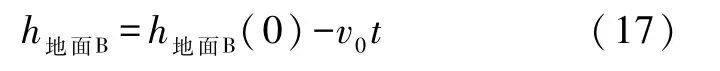
直接利用定义1和式(14)(或者对式(2)的第二式进行等时积分,并利用约定1)得 B中重力势能为
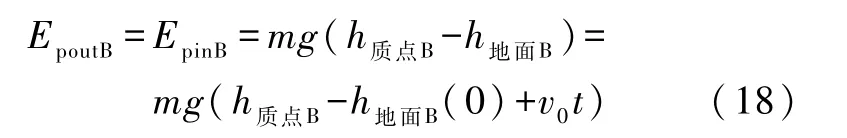
式(18)表明,EpoutB不仅与质点高度这一位形坐标h质点B有关,还显含时间t.这是由于在电梯上看,重力场的源(地球)是运动的.又由于质点所受作为外力的惯性力所作之功可以忽略不计,所以功能定理的式(1)给出系统机械能EB满足

其中
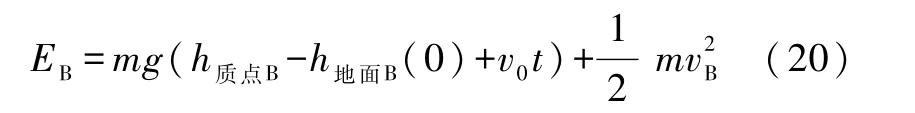
将式(18)代入式(19)得

此(近似)式与内力场处理的结果式(11)一致,表示系统的机械能不守恒.式(19)显示,系统在电梯中看机械能不守恒的根源在于外力场的势函数显含时间,而后者又根源于重力场源地球是运动的[9].
2.1.3在地球和质点的共同质心系C或相对于质心以匀速v0运动的惯性系D中的观察与在非惯性系A和B中的观察之比较
惯性系C和D与非惯性系A和B的差别确实很小,但下面的分析表明其中的观察结果的差异却不是都很小.对于内力场处理,无论在C或D中观察,都无其他力,且势能都不显含时间,故机械能都守恒(但是在A中机械能(近似)守恒,在B中不守恒,由(近似)式(11)表示).对于外力场处理,如果在C中观察,则无其他力,且作为重力场源的地球(近似)静止,故重力势能场(近似)不显含时间,因此系统机械能(近似)守恒(与 A中观察(近似)相同);如果在 D中观察,虽然无其他力,但是地球的速度(近似)为-v0,所以重力势能显含时间,因此系统机械能不守恒((近似)结果与 B中观察到的(近似)式(21)相同).
2.1.4对有关文献的澄清
文献[10]的例1对于同一问题采用了外力场处理,但是与本文的定义1及约定1不同,在电梯中和地面上势能零点各取本参考系的原点,从而得到了地面系和电梯系机械能都守恒的结果.但是这只是地面附近可近似视为均匀场的一种局部巧合.如果精确考虑,或范围扩大一点,地面系和电梯系中重力场便不能视为均匀场,此时即使采用文献[10]的势能零点取法,那么,地面系机械能守恒,而电梯系中重力场及其势能将显含时间,这违反了机械能守恒定理的条件(6),由定理1知机械能不守恒!顺便指出,该文的例2对于固联于运动车厢的斜面上的滑块,为了凑合出地面上看系统机械能也守恒的错误结论,将斜面作用于滑块的约束力所做之功独出心裁地说成是以“约束力势能的减小”为代价.事实上,如果一定要定义一个“约束力势能”的话,那就是斜面的弹性势能.然而由于刚性的斜面没有形变,其弹性势能永远为零,无法减小.十分明显,约束力对滑块所做之功其能量来源于滑块下滑过程中维持小车匀速运动的动力机械所消耗的电能或化学能.
2.2在地面上和在运动车厢里看一端固定于车厢壁的弹簧振子的机械能变化
文献[11]第113页至114页对运动车厢里的弹簧振子在地面上看机械能不守恒给出了一个简单的证明:如图2所示,“在车厢里光滑桌面上弹簧拉着一个物体m作简谐振动,车厢以匀速v前进.选弹簧和m作为我们的系统,厢壁在C点拉弹簧的力f是外力.以地面为参考系,dA外=f·vdt≠0,从而系统的机械能E振子=Ek+E弹簧in≠常量.换到车厢参考系,弹簧与厢壁的连接点 C没有位移,外力 f不作功,dA′外=0,系统的机械能=常量.”
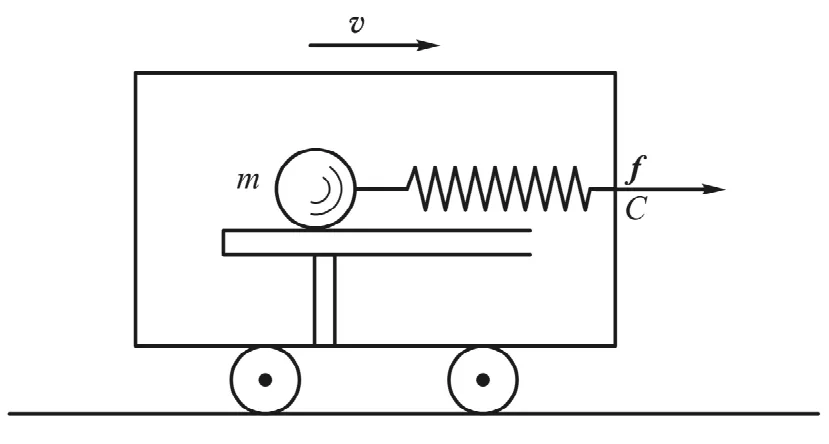
图2 运动车厢里的弹簧振子
这一证明基于文献[11]中已经强调的弹簧势能只由弹簧长度决定而与时间无关,故适用势函数与时间无关条件下的功能定理.也许有人要问,在多体(地球+车厢+弹簧+小球)的质心系统(惯性系)中看,由于弹簧的振动,地球和车厢都有微小的变化着的加速度因而不是严格的惯性系.小球要受到惯性力的作用,上述处理忽略了作为外力的惯性力的功是否合理呢?回答是,因为弹簧的拉力远大于小球受到的惯性力,故在地球或车厢中看,小球受到的惯性力都可以忽略不计,即地球和车厢都可以近似地视为惯性系.
在文献[11]的上述处理中,系统由一根质量可以忽略的弹簧和一个小球组成,车厢和地球是外界,这种描述方式可以称之为“实体模型”.文献[12,13]在“实体模型”下纠正了类似问题上文献[14]的错误观点.
我们还可以换一种等效的力场模型来处理这一问题.考虑到弹簧本身的动能忽略不计,对于小球和车厢壁而言,弹簧的唯一作用是以小球与其平衡点的距离为自变量按照胡克定律同时向小球和车厢壁提供相反的作用力,因此在地面和小车上可以分别用在相应的位形空间(x)和(x′)中假设车厢壁与小球之间存在服从胡克定律:
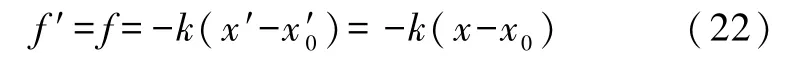
(其中 x0和 x′0=x0-vt分别为小球的平衡位置在地面和小车上的坐标)的有势力场取代弹簧实体的存在,从而系统可以被描述为质量为m的小球(质点)在车厢壁所提供的、遵从胡克定律式(22)的有势力场中运动.于是我们可以像例1一样等价地采用内力场处理和外力场处理.在内力场处理下,势能函数与时间无关 ,不是本文所重点关注的,为节省篇幅,建议读者参考文献[15]对类似问题的处理.下面只具体给出外力场处理.
与上面的定义1、定理3和约定1类似有定义2、定理4和约定2.
定义2 在外力场概念下小球的势能就是内力场概念下小球与车厢壁之间的相互作用势能.
定理4 小球的势能由小球与车厢壁之间的距离决定而与参考系无关.
约定2 小球在车厢中的平衡位置 x′0取为小球与墙壁之间相互作用势能的零点也即外力场势能的零点.
上面已说明小车和地球都可以近似地视为惯性系.系统的机械能是小球的动能加上小球在有势外力场中的势能.
在小车上看,等时积分式(2)的第二式,将式(22)代入并利用约定2得小球的势能为
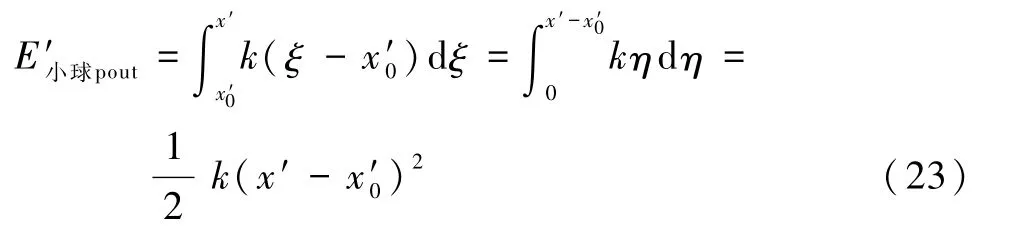
本模型除有势外力场外无其他作用力,故方程(1)给出系统的机械能E′小球满足
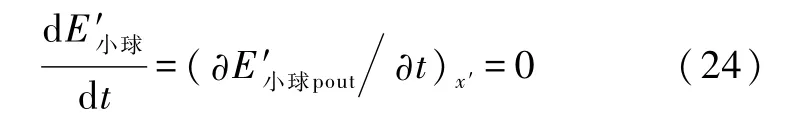
此式表明在小车上观察,系统的机械能守恒.
在地面上看,小球相对于小车的平衡位置x′0的地面系坐标x0是

由定理 4、约定 2和式(23)(或者等时(即等x0)积分式(2)的第二式,将式(22)代入并利用约定2和式(25))得小球的势能为
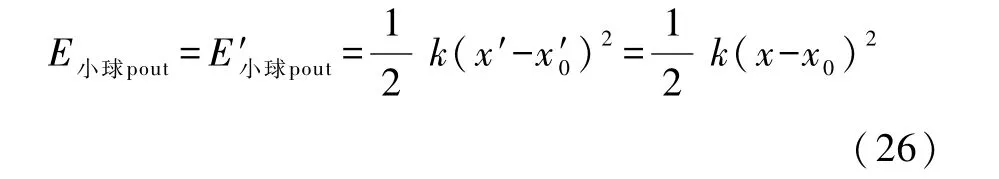
式(22)和式(26)表明,力场和势能函数的空间分布函数f和E小球pout不仅与小球的空间坐标 x有关,还与参数x0=x′0+vt有关,即显含时间t,其物理图像是整个外力场f及其势函数 E小球pout在 x空间以速度 v随时间平移,其物理根源是,在地面上看,胡克力场的源(墙壁)具有速度v.
本模型除有势外力场外,无其他力作用,故方程(1)简化为
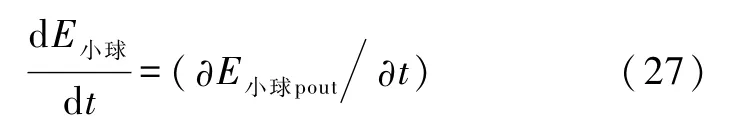
将式(26)代入式(27),并利用式(25)得

此式表明在地面上观察系统的机械能不守恒,除非v=0,即小车不开动.
以上结论与实体模型所得结论完全一致.
顺便指出,以外力场模型的观点看待文献[14,16]对类似问题的处理,那么其错误来自这些文献对于与时间有关的力场,将势能定义式(2)中的空间偏导数误解为空间全导数,从而将势能积分表示式(23)中负力的等时路径积分式误写为随体路径积分.后者根据动能定理实际上是系统动能的减少,作者们既然将它误解为系统势能的增加,当然就得到系统机械能守恒的错误结论了.
3 结论
与时间有关力场的功能定理确实具有广泛的使用价值,且其证明极其简单,值得在大学物理课程中列为选修内容或者思考题.过去由于某些文献的作者缺乏这方面的关注而导致的错误得到了原则上的纠正.
致谢:十分感谢北京大学赵凯华教授的有益讨论和建议.
[1] Kim,Sangrak.Validity of the work-energy theorem in molecular dynamics simulations for nanodroplets collisions[J].molecular simulation 2012,38(11):906-911.
[2] Russell Shawn,Bennett Bradford,Sheth Pradip.The gait of children with and without cerebral palsy:work,energy,and angular momentum[J].journal of applied biomechanics,2011,27(2):99-107.
[3] Won Sik L’Yi.Covariance of the Equations of Motion and the work-energy Theorem[J].New Physics∶Sae Mulli,2012,62(5):460-463.
[4] 朱如曾.相对性原理及其对自然界定律的协变性要求[J].大学物理,2000,19(2):15-26.
[5] 张建忠.对机械能守恒条件的讨论[J].集宁师专学报,2006,28(4):40-41.
[6] 陈滨.分析动力学[M].北京:北京大学出版社,1987:128.
[7] 高炳坤,谢铁曾.地球所受的一种易被忽视的惯性力[J].大学物理,1991(11):46-47.
[8] 郑理.动惯性系中的功能原理及机械能守恒定律[J].河北能源职业技术学院学报,2002(3):80-82.
[9] 赵文桐,刘文芳,刘明成.重力机械能守恒定律在各惯性系都成立[J].物理通报,2015(3):96-98.
[10] 赵凯华,罗蔚茵.新概念物理教程[M].2版.北京:高等教育出版社,2004:113-114.
[11] 朱如曾.弹簧振子相对于运动惯性系的机械能不守恒——关于“对一道中学生物理竞赛试题答案的商榷”的商榷[J].物理通报,2015(4):84-87.
[12] 孟照辉.运用机械能守恒定理解题的参照系问题—对“对一道中学生物理竞赛试题答案的商榷”的不同意见[J].物理教师,2015(2):94.
[13] 李学生,师教民.对一道中学生物理竞赛试题答案的商榷[J].物理通报,2014(9):119-120.
[14] 高炳坤.力学中一个令人费解的问题[J].大学物理,1995,14(5):20-21,24.
[15] 明成,刘文芳,赵文桐.弹力机械能守恒定律在各惯性系都成立[J].物理通报,2015(12):109-111.
Work-energy theorem for systems with time related force field and its application
ZHU Ru-zeng
(State Key Laboratory of Nonlinear Mechanics(LNM)and Key Laboratory of Microgravity,Institute of Mechanics,Chinese Academy of Science,Beijing 100190,China)
The work-energy theorem for systems with time related force field possessing potential and other forces has more powerful application value than the ordinary work-energy theorem.This paper plans to introduce the former and apply it to judge whether the mechanical energy relative to different reference systems is conservative for two simple systems:a particle in the gravity field and a light spring oscillator with one end fixed in the moving compartment.
time related field;work-energy theorem;theorem of mechanical energy conservation;gravity field;light spring oscillator
O 301
A
1000-0712(2016)10-0011-06
2014-12-01;
2016-05-13
朱如曾(1941— ),男,江苏靖江市人,中国科学院力学研究所研究员、博士生导师,主要从事物理力学等研究工作.

