利用气体分子相对速度的各向同性导出平均相对速率
郑 勇
(黔南民族师范学院 物理与电子科学学院,贵州 都匀 558000)
利用气体分子相对速度的各向同性导出平均相对速率
郑 勇
(黔南民族师范学院 物理与电子科学学院,贵州 都匀 558000)
首先通过类比发现理想气体分子相对速度分布与速度分布具有相同的函数形式,但是困难在于确定前者的常数因子.我们发现一个常用的公式恰好可以帮助确定这个常数.最终通过类比平均速率的推导直接得到了平均相对速率公式.
理想气体;平均相对速率;推导
事实上,用速度分布计算平均速率的过程学生是比较熟悉的
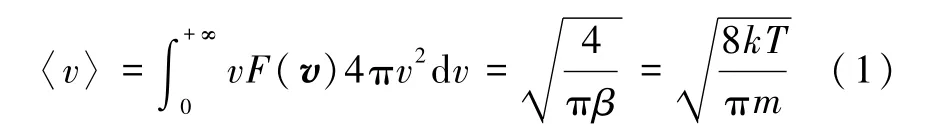
理想气体中任意两个分子的速度 v1和 v2显然是相互独立的;二者之间的相对速度 u=v2-v1是一个独立的物理量,具有各向同性的特点,与分子速度v类似,其 3个分量 ux、uy、uz也是统计无关、相互等价的.u与 v具有的统计性质是完全等同的,因此,它们的分布函数都只与其大小有关,都可写成3个分量分布函数乘积的形式.从这些相同的统计性质定出的二者的分布函数在形式上显然应完全相同.
因此,与速度分布函数F(v)对比,我们可以直接写出相对速度分布满足的函数形式
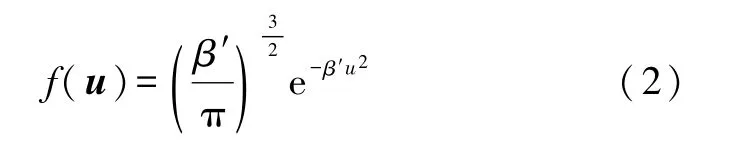
其中β′是待定常数.
但是我们面临如何确定常数β′的问题.
在讨论对速度分布函数时,常数β可以通过比较能量均分定理给出的关系式以及由分布函数算出的确定,结果是;但是对于相对速度,虽然由式(2)仍然有,但是没有了能量均分定理给出的关系式.
为克服这一点,注意到如下公式[3]:

其中由于各向同性,v1和v2的平均值都为零,所以,〈v2·v1〉=〈v2〉·〈v1〉=0.
将式(4)与〈u2〉=比较,刚好可以用来确定常数β′,结果是(5)
代入式(3),我们便得到最终的平均相对速率表达式:
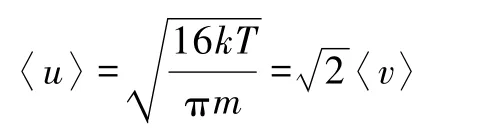
以上讨论还可以推广到同一系统中两种质量不同的分子间的平均相对速率的计算.若两种分子质量分别为m1、m2,此时式(4)变为
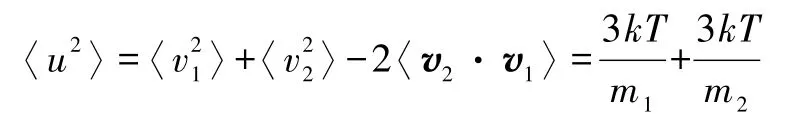
于是
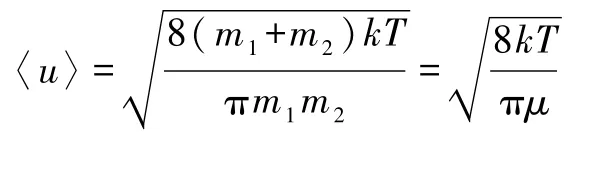
从整个推导过程可以看出,与通常用麦克斯韦速度分布讨论气体分子相对速度分布、计算平均相对速率的方法不同,我们充分利用了分子相对速度具有各向同性的特点,用类比的方法计算平均相对速率.这种思路的关键是要能确定出分布函数中的待定常数,对于速度分布函数,能量均分定理可以帮助完成这一点;而对于相对速度分布,类似关系也被我们找到.整个推导完全按照类比的思路进行,便于学生接受.
[1] 李洪芳.热学[M].北京:高等教育出版社,2001:230-232.
[2] 刘伟涛,张婷,李承祖.气体分子平均相对运动速率的推导[J].大学物理,2011(12):36-37.
[3] 赵凯华,罗蔚茵.热学[M].北京:高等教育出版社,1998:71-78.
Deriving the average relative speed of gas molecules with the isotropy
ZHENG Yong
(College of Physics and Electronics,Qiannan Normal College for Nationalities,Duyun,Guizhou 558000,China)
The relative velocity distribution of molecules of ideal gas is found to possess the same function form as the velocity distribution,which is due to the similar statistical properties they satisfy.The constant in this function is difficult to determine for the former and we have completed this by employing a familiar relation which generally being used in an approximate discussion of the average relative velocity.Then the average relative velocity is calculated.
ideal gas;average relative velocity;derivation
物理实验
O 414.2
A
1000-0712(2016)10-0028-01
2015-10-21;
2016-03-12
贵州省教育规划青年课题(2014C031)资助
郑勇(1983—),男,四川宜宾人,黔南民族师范学院教师,主要从事凝聚态理论研究和基础物理教学工作.
——黔南示范小城镇集锦(之二)

