孔内抽水引起的桩周地表沉降计算方法研究

刘金海，吴霞，王娟

（1.赣州中科工程管理有限公司，江西赣州 341000；2.江西应用技术职业学院，江西赣州 341000；3.陕西铁路工程职业技术学院，陕西渭南 714000）

孔内抽水引起的桩周地表沉降计算方法研究

刘金海1，吴霞2，王娟3

（1.赣州中科工程管理有限公司，江西赣州 341000；2.江西应用技术职业学院，江西赣州 341000；3.陕西铁路工程职业技术学院，陕西渭南 714000）

针对富水地区桩基工程施工中桩孔内渗水量较大的特点，考虑桩基孔内抽水导致水位下降而引起桩周地表沉降，分析一种潜水完整井稳定渗流下的桩周地表沉降计算方法。根据渗流理论分析推导了降水渗流下桩基周围土体单元的有效应力增量；采用二维平面范围内进行二重积分计算的方法，分析了渗流作用下孔内降水引起的桩周地表沉降计算公式。以具体工程为依托，分别采用现场实测与公式计算的方法对桩周地表沉降进行预测，结果表明实测值与计算值整体上较为接近，但在距离桩孔边缘3 m范围内，实测值大于计算值，而5 m范围外的计算值与实测值较为接近，同时沉降值随着与桩孔边缘距离的增大而减小。

桥梁；桩基础；桩周沉降；渗流；富水地区

在地下水位较丰富的地区，桩基在成孔掘进过程中易受到地下水的影响。桩孔的开挖掘进为孔周土体的侧向移动提供了临空面，并为地下水的渗流提供了新路径。与大型基坑开挖相比，桩基孔成孔中桩孔开挖面范围较小，相关研究与大量工程实际表明，由于土体开挖而引起的桩孔周围土体的侧向位移和竖向沉降较小，在实际分析计算时应主要考虑由于地下水的降水渗流所引起的沉降。

桩基孔内抽水导致地下水位下降，一方面使孔隙水压力得以消散而转移为有效应力，桩周土体单元的自重有效应力增大，土颗粒的接触更紧密。另一方面，孔内降水导致孔内外存在水头差，根据渗流理论，在水头差作用下降水竖向渗流会给土颗粒施加单位体积上的动水压力，使土颗粒产生附加沉降。自重有效应力的增加和竖向动水压力都会导致土颗粒更加密实而固结，在竖向表现为沉降。显然，土体的沉降与土单元的应力变化有直接联系，而桩孔内抽水势必引起地下水位下降，进而引起桩孔周围土体应力发生变化。该文根据渗流理论和固结理论，分析桩基孔周土体在孔内抽水条件下的地表沉降，推导其沉降计算公式。

1 降水对孔周土有效应力的影响

孔内抽水会导致孔周土体中的地下水位下降，土体单元的自重有效应力和渗流有效应力增长（见图1）。假设沿地表水平方向为X方向，沿土体深度方向为Y方向；在土体h深度处取任意一土体单元，该单元在X、Y、Z 方向的长度分别为d X、d Y、1；原始地下水位深度为h0，孔深为H；地下水位以下的土体处于饱水状态，h0深度范围内土体的重度为γ0，地下水位以下土体的重度为γ′，孔隙水压力为σw，降水为潜水完整井稳定流。在开挖掘进中，不考虑施工动载对桩孔周围土体初始应力的影响。

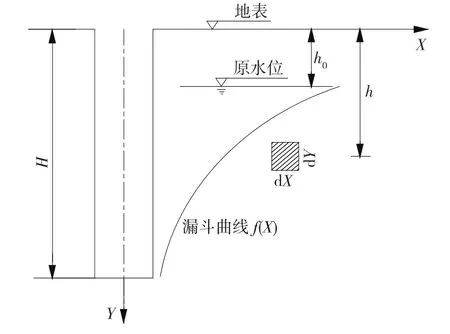
图1 降水漏斗示意图

1.1 自重有效应力变化

在地下水位未下降前，对于水位以下的土体单元，其应力由土颗粒和孔隙水压力共同承担；在水位下降后，孔隙水压力得以消散，土颗粒失去上浮力，在自重作用下所承担的接触应力将增大，通过土颗粒接触产生的有效应力得以增长。

水位下降前，水下h深度处土体单元的有效应力σ′=σ-σw，其中总应力σ=h0γ0+（h-h0）γ′，孔

隙水压力σw=（h-h0）γw。因此，水位下降前土体单元的自重有效应力为：

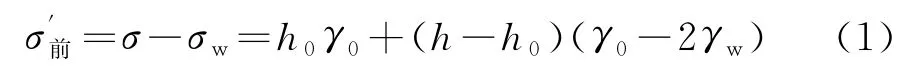
在水位下降超过h深度后，h深度处土体单元的应力仅有自重应力，该土体单元的有效应力为：

水位下降前后h深度处土体单元的有效应力增量为：

式（3）中的变量均为已知，将其数值代入便可求出水下任意深度处土体单元的有效应力增量。

1.2 渗流有效应力变化

孔内抽水引起水头差，并为地下水的渗流提供了新路径。根据渗流理论，地下水在水头差作用下产生渗流时将给土颗粒施加体积上的动水压力，当这种动水压力的方向向下时，土颗粒将在水压作用下产生下沉而变得更加密实。

土颗粒的下沉产生竖向沉降，而土颗粒的下沉值显然与动水压力的大小有关。在动水压力值的求取方面，苑莲菊等认为作用在一个单位体积土体单元上的动水压力值与水力坡降i有关，其表达式为：

动水压力Dw赋予了土颗粒附加的渗流有效应力。为了求取渗流有效应力，假定渗流仅发生在竖向，此时渗流有效应力可通过计算作用在体积V土体上的动水力与过水面积A的比值来求取，即：式中：体积V等于面积A乘竖向过水路径h过。

式中：f（X）表示漏斗曲线函数，变量为水平X方向的距离。

将式（4）、式（6）代入式（5），得渗流有效应力：

2 地表沉降计算分析

2.1 地表总沉降分析

桩基孔内抽水，孔周土体地下水水位将下降，土体单元的自重有效应力与渗流有效应力均产生变化增量。自重有效应力与渗流有效应力的作用方向均向下，有效应力增量对土体单元将产生向下的压缩。钱家欢等认为土体单元在应力增量作用下所产生的微小竖向压缩可用下式表示：

式中：d s为竖向微小压缩；Δp为应力增量；e0为土的初始孔隙比；a为压密系数。

将有效应力增量和渗流应力增量分别代入式（8），得到两种有效应力下所产生的微小压缩，分别记为d s1和d s2，其表达式为：

自重有效应力和渗流有效应力均会导致土体产生竖向微小压缩，故由于降水渗流而产生的土体竖向微小压缩量d s=d s1+d s2。

假设桩孔周围土体中的土颗粒在竖向是相互连续接触的，则当单元土体产生竖向压缩时，该单元体上部的单元体将同时向下移动，并依次相互影响而最终传播至地表。根据随机介质理论，土体中微小竖向压缩的累加将在地表产生一微小单元凹面，该凹面中心的竖向沉降值Wd按下式计算：

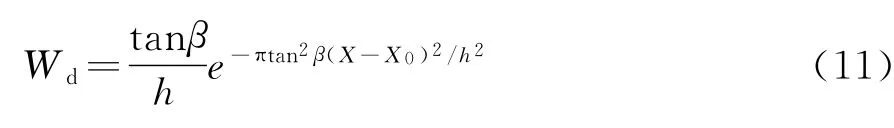
式中：β为桩孔所在地层的影响范围角，一般可根据前期地质勘察资料获得；X0为单元体水平方向的边缘中心点至桩孔边缘的距离（m）。

显然，若能对该降水漏斗范围内的全体微小单元凹面在X和Y轴构成的区域进行二维重积分计算（仅以二维平面计算），便可计算出降水漏斗范围内的地表沉降，即地表沉降可表示为：

2.2 沉降分类计算分析

桩孔周围在降水渗流过程中，土体沉降由两部分贡献而成：一部分是自重有效应力增量；另一部分是渗流有效应力增量。桩周土体的漏斗曲线随着降水的不断进行而产生变化，漏斗曲线以上部分的土体将变为疏干状态，以下部分的土体则处于渗流状态。因此，在原水位线至漏斗曲线之间的这部分土体的沉降是由自重应力增量引起的，接触应力增大，土颗粒变得更加密实；而漏斗曲线以下至孔内水位顶面之间的这部分土体的沉降是由渗流动水压力引起的（见图2）。在计算地表沉降时，应以漏斗曲线为分界线，将桩周土体划分为两大区域进行二维重积分运算。

图2 沉降计算示意图

对于原水位线至漏斗曲线之间的这部分土体，其积分区间，X方向为0～R，Y方向为h0～f（X），则此时沉降值的计算式为：

对于漏斗曲线以下至孔内水位顶面之间的这部分土体，其积分区间，X方向为0～R，Y方向为f（X）～（H-h0），则此时沉降值的计算式为：

地表总沉降为：

地表总沉降计算的关键在于确定漏斗曲线的变化方程f（X）。根据裘布依公式和流量相等性（即相同时间内通过距桩孔轴线不同距离的过水断面的水流量相等），燕建龙等计算了稳定潜水完整渗流下的漏斗曲线方程，其表达式为：

将式（16）代入式（15），即可得到地表沉降值。

3 工程实例

以广西河池市某桩基工程为依托，采用上述计算公式对孔内抽水条件下的地表沉降进行计算。

该桩孔场地位于农田内，开挖深度为12 m，其地下水以上层滞水和潜水为主。广西河池地区雨水丰富，属于岩溶地区，地下水丰富，其上层滞水易受大气降水影响。实际开挖中，孔内涌水量较大，为保障孔体的稳定，进行孔内抽水减压处理。地层的主要参数如下：压密系数a=0.36；初始孔隙比e0= 0.68；地层影响范围角的正切值为1.12；水力坡降的影响范围半径为108 m，水力坡降i=0.06。

同时对地表沉降值进行监测验证计算结果的有效性。为了防止地表沉降对观测基准点造成影响，实际监测时将基准点布置在稳定的基岩上，设置3个观测基准点，以便通过联测验证观测的稳定性。观测点从桩孔边缘开始设置，每隔2 m设置一个并逐渐远离桩孔，共设置11个观测点。理论上第一个观测点应设置在桩孔的边缘，但该设置方式有碍于实际施工作业，故将第一个观测点设置在距离桩孔边缘1 m的地方。

图3为计算结果与实测结果比较。从中可看出：实测值与计算值整体上较为接近，但在距离桩孔边缘3 m范围内，计算值与实测值差异较大，实测值大于计算值；而5 m范围外计算值与实测值较为接近，同时沉降值随着与桩孔边缘距离的增大而减小。图4为由于孔内抽水而导致的农田地表开裂。

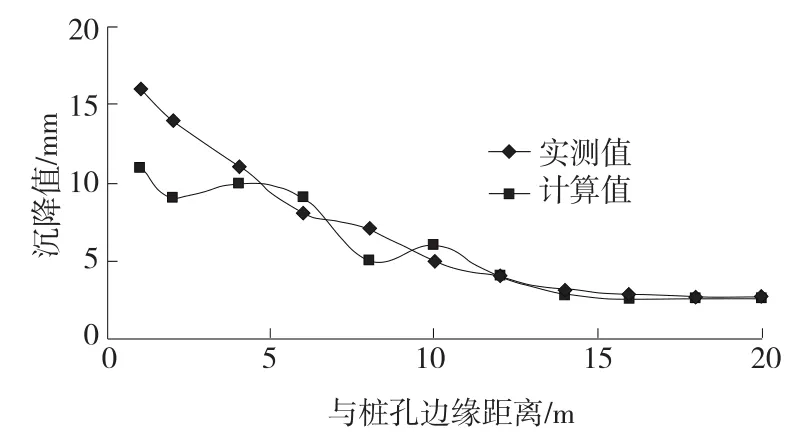
图3 地表沉降实测与计算结果对比

图4 桩孔内抽水导致的地表开裂

在距离桩孔边缘3 m范围内，实测值大于计算值，这是由孔内抽水导致孔周近距离范围内土体中的土颗粒流失所致，而该文的计算分析是建立在孔周土体中土颗粒始终保持紧密接触的假设之上，即存在一定的误差，但这种误差会随着与桩孔边缘距离的增大而减小。

4 结语

该文根据渗流与固结理论，分析了桩基孔内抽水引起的桩孔周围地表沉降的计算方法，工程实践表明该计算方法具有一定的实用性。

在桩孔边缘近距离范围内，现场实测结果大于计算结果，推测这与分析计算时没有考虑桩周土体中土颗粒的流失有关，在这方面有待改进。这也表明在分析桩周地表沉降时不可忽视桩周土体中土颗粒流失对地表沉降的影响。

［1］ 王一新，姚小平，孙荣玲.大跨度上承式拱桥施工监控技术［J］.河南理工大学学报：自然科学版，2014，33（2）.

［2］ 周益军，高燕希，杨进.隧道开挖时地下渗流场的模拟分析［J］.公路与汽运，2008（4）.

［3］ 温世儒.基于超前地质预报的隧道施工期风险评估及防控措施研究［D］.西安：长安大学，2012.

［4］ 贾强，张鑫，应惠清.桩基础托换开发地下空间不均匀沉降的数值分析［J］.岩土力学，2009，30（11）.

［5］ 袁聚云，钱建国，张宏鸣，等.土质学与土力学［M］.北京：人民交通出版社，2010.

［6］ 徐春华，孙建波.桩基融沉附加力三维问题的积分方程解法［J］.施工技术，2012（增刊1）.

［7］ 陈希哲.土力学与地基基础［M］.北京：清华大学出版社，2004.

［8］ 苑莲菊，李振栓，武胜忠，等.工程渗流力学及应用［M］.北京：中国建材工业出版社，2001.

［9］ 钱家欢，殷宗泽.土工原理与计算［M］.北京：中国水利水电出版，1996.

［10］ 韩煊，李宁.隧道施工引起地层位移预测模型的对比分析［J］.岩石力学与工程学报，2007，26（3）.

［11］ 燕建龙，赵治海，杨利全，等.基坑降水设计中水文地质参数计算方法分析探讨［J］.工程勘察，2011（3）.

U443.1

A

1671-2668（2016）06-0213-04

2016-02-20