基于模糊PID控制的ABS系统研究
张利,宋年秀,于明晓
(青岛理工大学汽车与交通学院,山东青岛 266520)
基于模糊PID控制的ABS系统研究
张利,宋年秀,于明晓
(青岛理工大学汽车与交通学院,山东青岛 266520)
在MATLAB/Simulink中建立汽车制动防抱死系统(ABS)仿真模型,以单轮车辆模型为研究对象,以模糊PID控制器为控制模块,对ABS模型进行仿真研究。结果表明基于模糊PID控制器的ABS系统能根据变化时刻对相关参数进行调节,能适应不同路面,且都能达到良好的制动效果。
汽车;制动防抱死系统(ABS);模糊PID控制器;制动效果
制动系统是车辆安全系统的重要组成部分之一,制动性能也是保证车辆安全行驶的必要性能。大多数交通事故是由于汽车紧急制动时车轮抱死引起的,制动防抱死系统(ABS)可防止车轮抱死,从而减少这类事故。而ABS控制器是ABS装置的核心,因而研究ABS控制器是非常必要的。目前有很多控制算法,各控制算法都有各自的利弊,当路面状况改变时,单一控制器不利于车辆的制动。PID控制器是具有比例、积分和微分控制规律的控制器,可控制汽车在制动时的滑移率,且控制算法简单、稳定性较好,但不能满足汽车制动时的实际工况。模糊控制不要求控制对象具有精确模型,并有较强的适应性和鲁棒性。因此,采用模糊PID控制算法能充分发挥PID控制器和模糊控制两种算法的优点。
1 ABS的动力学建模
1.1 理论依据
汽车制动时利用的是地面与轮胎之间的摩擦,使轮速与车速之间产生速度差,这种状态即为滑移现象。最佳车轮滑移率为15%~25%,此时汽车在制动或转向时都可获得较大的侧向力。一般把20%称为最佳滑移率。
1.2 车辆动力学模型
单轮车辆模型主要用于研究汽车的制动性能,可利用该模型分析ABS系统的制动问题。车辆受力分析如图1所示。
研究单轮车辆模型制动过程时不考虑空气阻力和滚动阻力对汽车的影响,由此可得出车辆动力学方程,其中车辆运动方程为:

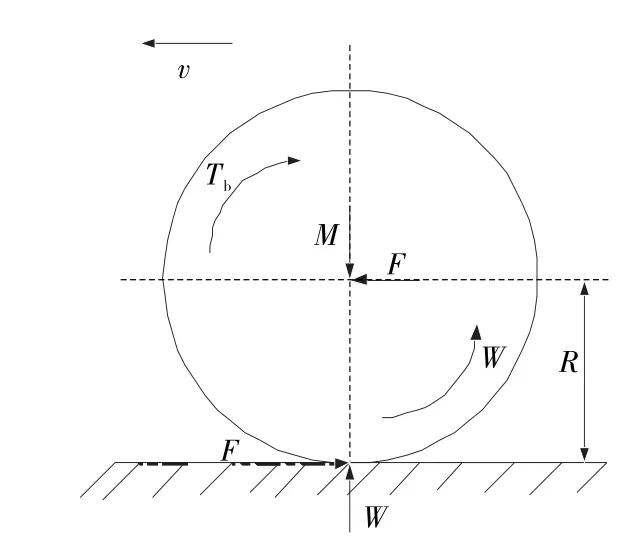
图1 车辆受力分析示意图
车轮运动方程为:

车辆纵向摩擦力为:

式中:M为汽车质量的1/4(kg);v为车辆行驶速度(m/s);F为汽车纵向附着力(N);I为车轮转动惯量(kg·m2);ω为车轮转动角速度(rad/s);R为车轮半径(m);Tb为制动力矩(N·m);μ为纵向附着系数。
由式(1)~(3)建立Simulink车辆仿真模型,以制动力矩Tb和纵向附着系数μ为输入量,输出量为车轮转速ω、车辆速度v和车辆制动距离s,仿真模型如图2所示。
1.3 轮胎模型
轮胎模型是指车辆制动时轮胎附着力与其他参数间的函数关系。除滑移率外,运行车速、路面状况、天气及轮胎花纹、结构等都是影响汽车行驶时附着系数的因素。但现实中大多数影响因素是变量,很难得到这些参数与附着系数的关系式。但滑移率与附着系数的关系式可以得到,可按照表达式建立
模型。采用应用广泛的双线性模型(如图3所示)。

图2 车辆动力学仿真模型
1.4 制动系统模型
制动系统包含传动机构和制动器,制动系统模型同样包括传动机构模型和制动器模型。传动机构模型采用液压机构,为了简化系统,不考虑其他因素的影响,主要考虑电磁阀电流与制动压力的关系。传递函数为:

式中:K为环节增益;S 为电磁阀的响应时间;T为时间常数。
由于电磁阀的响应时间通常小于或等于10 ms,惯性过程的参数T取0.01,K取100。
制动器模型是指制动器力矩与制动液压之间的关系模型。为了简便控制算法,假定制动器的非线性特性很弱且不考虑传送滞后的影响。制动器表达式如下:

式中:k为制动器制动系数(N·m/k Pa);p为制动压力(k Pa)。
由式(4)、式(5)建立的制动系统仿真模型如图4所示。

图4 制动系统仿真模型
1.5 滑移率计算公式
制动时车辆的滑移程度一般用滑移率表示,其计算公式见式(6),仿真模型如图5所示。


图5 滑移率计算模型
2 模糊PID控制器设计
2.1 控制系统结构设计
模糊PID控制器的输入量为误差e和误差变化率ec,要求根据不同时刻的e和ec对PID参数进行整定和修改,组成模糊PID控制器,系统结构如图6所示。
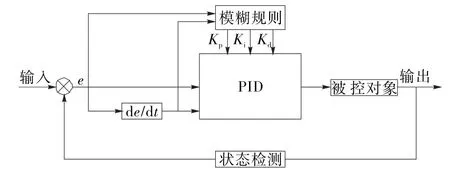
图6 模糊PID控制系统的结构
2.2 隶属度函数的确定
PID参数自整定通常要求控制器为两输入三输出,输入量为误差e和误差变化率ec,输出变量为ΔKp、ΔKi和ΔKd。依据经验,定义输入量e 和ec的范围为[-3,3],模糊子集为{NB,NM,NS,ZE,PS,PM,PB};输出量ΔKp、ΔKi和ΔKd的范围为[0,1],模糊子集为{ZE,PO,PS,PM,PB}。输入、输出隶属函数如图7、图8所示。
通过调整参数ΔKp、ΔKi和ΔKd,实现系统的自适应模糊PID控制。调节计算式为:

图7 e和ec的隶属度函数
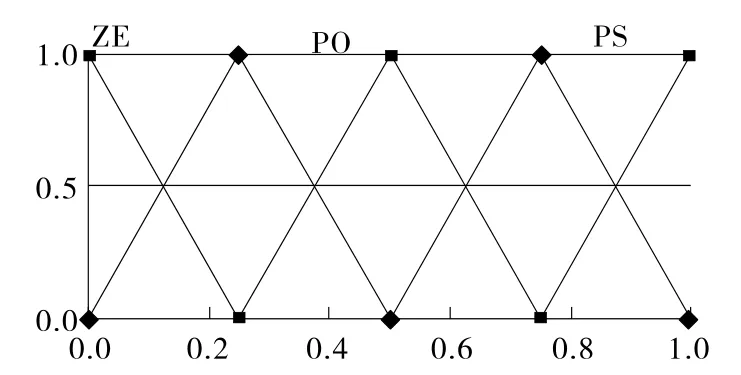
图8 ΔKp、ΔKi和ΔKd的隶属度函数
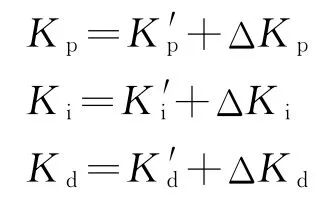
式中:K′p、K′i、K′d为原先整定好的PID参数。
2.3 确定模糊控制规则
通常要求Kp、Ki和Kd在不同e和ec的控制下。制动开始时e较大,应选择较大的Kp和较小的Kd,保证系统有较好的追踪效果,为防止系统超调过大,一般取Ki=0;当e和ec为中等大小时,为保证超调减小,选择较小的Ki,但Kp、Kd的大小要合适;当e较小时,为保证系统有较好的稳定状态,应增大Kp和Ki,选择适中的Kd。ΔKp、ΔKi和ΔKd的模糊规则如表1~3所示。
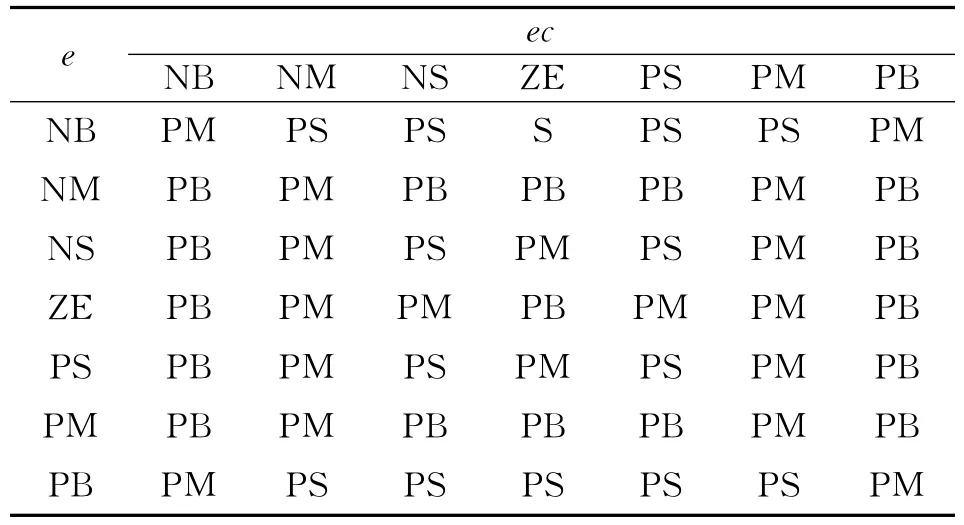
表1 ΔKp的模糊规则
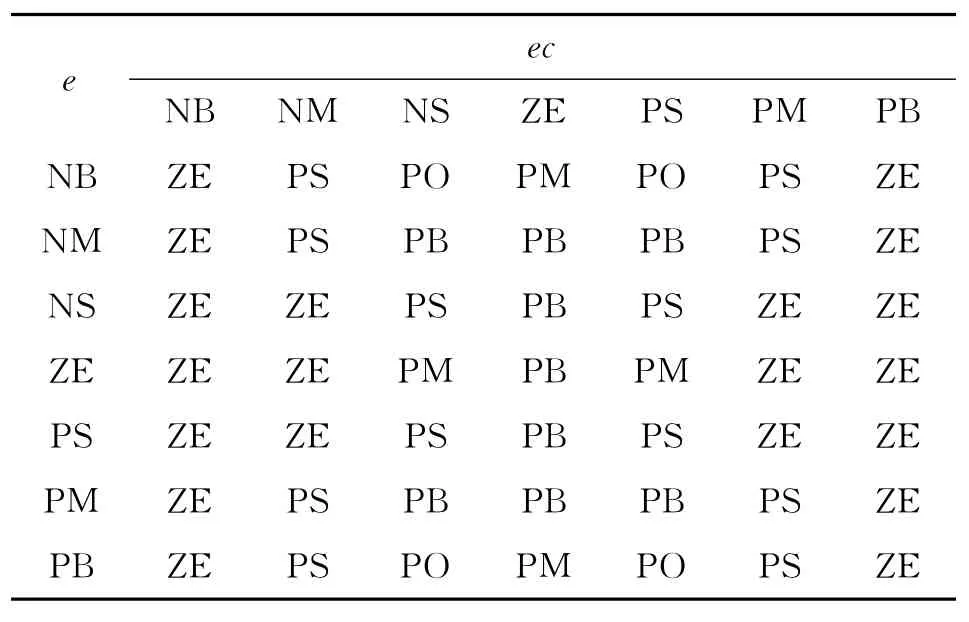
表2 ΔKi的模糊规则
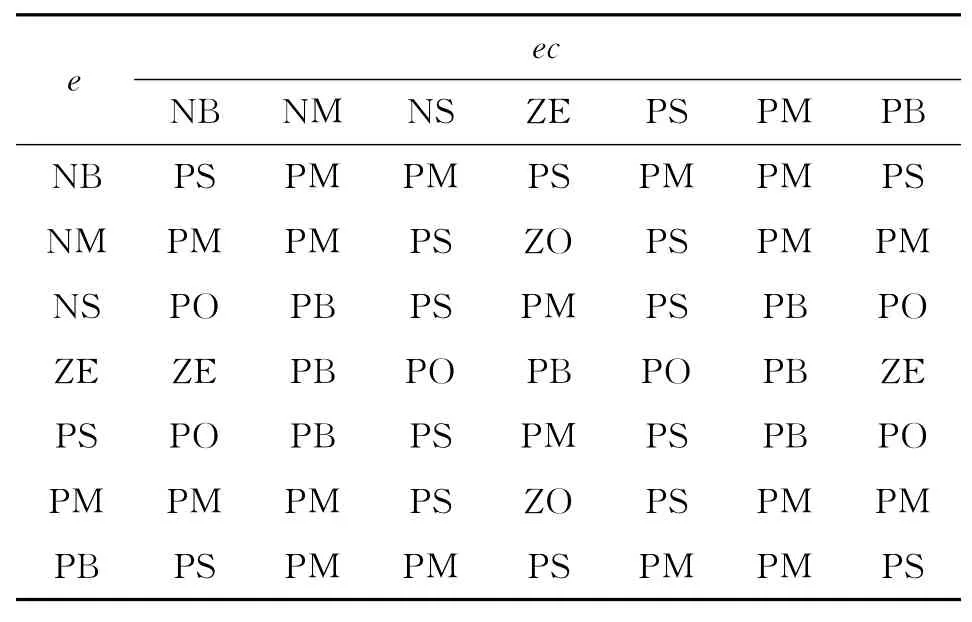
表3 ΔKd的模糊规则
2.4 解模糊化
按照模糊控制规则推理后,要反模糊化计算整定的3个参数,并得到输出量。采用重心法,计算方法见式(7)。模糊PID控制仿真模型如图9所示。


图9 模糊PID控制仿真模型
3 ABS系统仿真及结果分析
3.1 ABS系统仿真
借助Simulink,在不同路面上对模糊PID控制的ABS进行制动仿真。以某轿车为例,初始速度取25 m/s,1/4质量M为375 kg,车轮半径R为0.3 m,车轮转动惯量I为4.8 kg·m2,ABS系统仿真模型如图10所示。

图10 ABS系统仿真模型
3.2 仿真结果分析
在干、湿沥青路面上分别进行车辆仿真,得到轮速、车速和滑移率的关系曲线(如图11~13所示)。
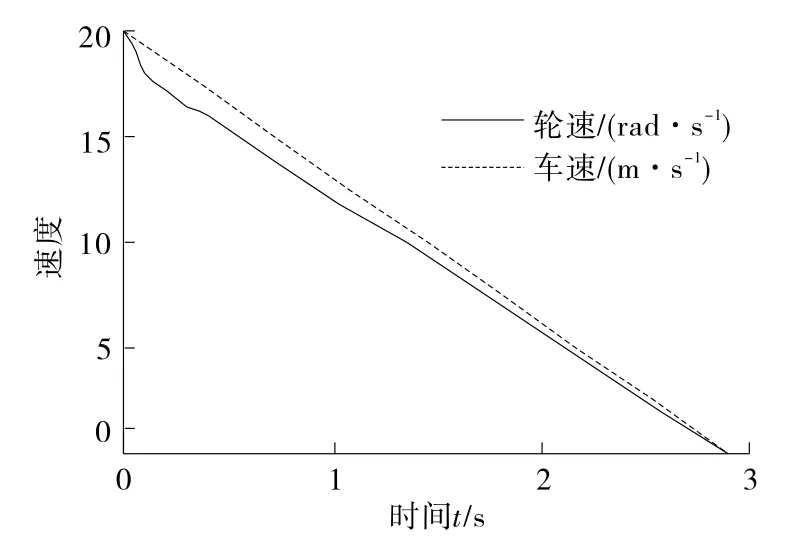
图11 干沥青路面上车速和轮速曲线
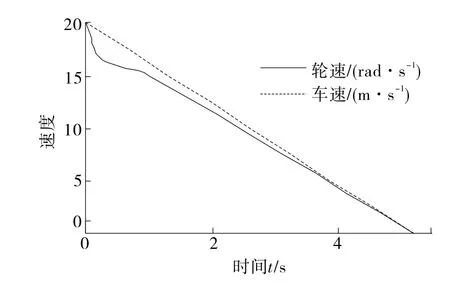
图12 湿沥青路面上车速和轮速曲线
由图11~13可知:1)汽车在干、湿沥青路面上制动时,滑移率分别达到0.18、0.15附近后基本保持不变,且制动时间可达到要求,说明模糊PID控制器控制的ABS能满足制动要求。2)模糊PID控制器控制的ABS在不同路面上虽然滑移率发生改变,但制动过程都能保持平稳,说明设计的模糊PID控制器能适应不同路面上的制动。
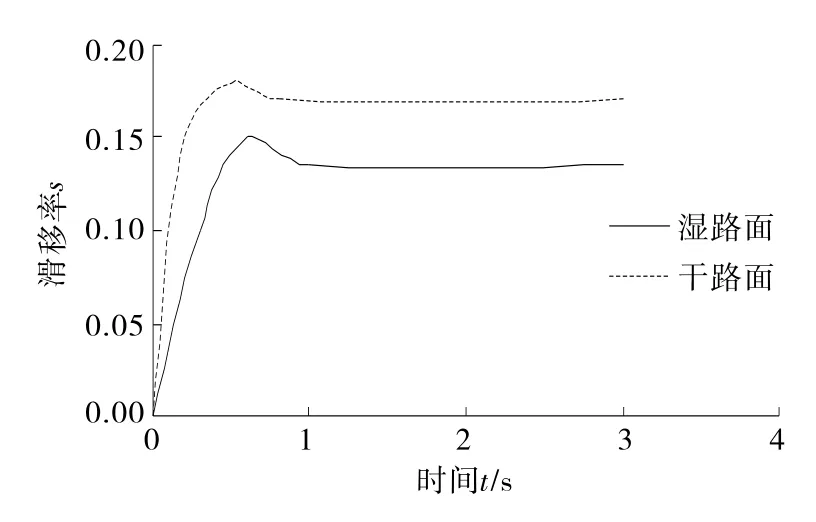
图13 两种路面上滑移率对比曲线
4 结论
该文借助MATLAB软件并依据ABS控制系统的特点设计ABS模型和模糊PID控制器,仿真分析其在不同路面上的制动效果。结果表明模糊PID控制器控制的ABS在干、湿两种路面上都可达到安全性能要求,制动过程中方向均保持稳定状态,模糊PID控制器可适应不同的路面,而且对于优化ABS的性能有效。
[1] 张颖,袁朝辉.汽车防抱死系统的模糊PID控制算法研究[J].计算机仿真,2010,27(12).
[2] 余志生.汽车理论[M].北京:机械工业出版社,2009.
[3] 张振生.基于模糊PID控制的ABS仿真研究[J].北方交通,2008(5).
[4] 付尔第.汽车防抱死系统建模仿真及控制方法的研究[D].锦州:辽宁工业大学,2014.[5] 吴玲,孙宇.基于Matlab/Simulink的汽车ABS系统建模与仿真[J].自动化应用,2014(5).
[6] 席本强,何毅.汽车ABS的模糊自适应PID控制[J].辽宁工程技术大学学报:自然科学版,2014,33(11).
[7] 李欢,何锋,蒋雪生.基于模糊控制的气电混合动力客车控制策略研究[J].客车技术与研究,2015(1).
[8] 武恺航,李勇,吴旻骏,等.基于模糊控制的气压ABS建模方法[J].公路与汽运,2012(6).
[9] 陈宁,黄会明,吴汶芪.基于模糊控制的电动汽车电子差速设计[J].客车技术与研究,2013(3).
[10] 王立平,李守成,刘英杰.基于Matlab/Simulink的半挂汽车列车防抱死制动系统仿真研究[J].拖拉机与农用运输车,2011,38(6).
U463.52
A
1671-2668(2016)06-0009-04
2016-05-10

