基于随机约束的快速公交发车间隔优化研究*
谢昀珊,杨信丰,徐静
(兰州交通大学交通运输学院,甘肃兰州 730070)
基于随机约束的快速公交发车间隔优化研究*
谢昀珊,杨信丰,徐静
(兰州交通大学交通运输学院,甘肃兰州 730070)
为了更好地发挥快速公交高效、便捷和经济的优势,需确定合理的发车间隔。文中在已有研究的基础上考虑乘客需求和快速公交走行时间的不确定性,利用随机机会约束规划的方法研究单条快速公交线路的发车间隔,建立了在一定置信水平下各成本最小的多目标随机机会约束规划模型,并设计了微粒子群与随机模拟相结合的混合智能算法进行求解;以兰州市快速公交线路B1为例进行验证,结果表明按该模型优化后乘客的在站等车时间和拥挤度均有所降低,该模型和算法合理可行。
城市交通;快速公交;随机机会约束规划;发车间隔;混合智能算法
快速公交是利用改良的公交车辆行驶在公交专用车道上的一种公共交通方式,具有便捷、舒适、容量大、运力高、投资少、见效快等特点,是提高公共交通吸引力和竞争力的主要途径之一。科学合理的发车间隔是发挥快速公交高效运营效果的前提,考虑快速公交运行时间及客流的不确定性,进一步研究快速公交的发车间隔对发挥其高效、经济和环保的优势具有重要意义。
对于公交发车间隔的优化,Furth P.G.等以最大化社会利益为目标,以总的补贴、车队规模和乘客满载率水平为约束建立了发车频率优化模型;Ceder A.等分析了确定最优发车间隔的方法,提出了确定发车间隔的3个步骤;Parbo J.等从用户角度对发车频率进行研究,建立了发车频率优化模型;孙芙灵根据乘客需求确定发车间隔,引入时段配车数概念并根据西安客流调查数据探讨了发车间隔的确定方法;牛学勤等以企业和乘客综合满意度为目标,建立了常规公交发车频率优化模型,并利用遗传算法进行求解;宋瑞等考虑乘客需求和常规公交站间走行时间的不确定性,以企业利益最大为目标建立了机会约束规划模型;张东等综合考虑乘客的出行时间、候车时间及滞留率等因素建立了快速公交发车频率优化模型。
该文在已有研究成果的基础上,考虑快速公交站间走行时间和乘客到达率的随机性,应用随机机会约束规划方法,研究快速公交车辆运营时间成本、乘客等车时间成本及乘客在车拥挤度如何在一定置信水平下最小化的多目标快速公交发车间隔优化问题,建立随机机会约束规划模型并利用混合智能算法进行求解。
1 模型的建立
快速公交运行过程较复杂,建立模型前应对实际情况进行概括和简化。在分析实际运行的基础上作如下假设:1)运营车辆全部为全程车且为同一车型;2)候车乘客先到先上车;3)车辆行驶过程中无超车现象;4)车站的乘客到达率服从均匀分布。
变量设置:i表示快速公交车辆,i=1,2,3,…,I;I为快速公交车辆数;j表示快速公交线路上的车站,j=1,2,3,…,J;J为快速公交线路上的车站数;rj为研究时段内第j个车站的乘客到站率,服从均匀分布;fi,j为第i辆公交车离开第j 个车站的时刻,当j=1时,为第i辆公交车的发车时间;Tj为研究时段内第i辆公交车在车站j-1和车站j之间随机行驶时间,服从正态分布;h为研究时段内快速公交发车间隔;hmin、hmax分别为研究时段内发车间隔的最小、最大取值范围;Si,j为第i辆快速公交车在第j个车站的停站时间,令S1,1=0;tud为人均上下车时间;tdi,j为第i辆公交车到达第j个车站的时间,当j=1时,为第i辆公交车的发车时刻;tk为公交车开关车门的时间;m为公交车座位数;tw为乘客能忍受的最大等待时间;qi,j为第i辆车离开第j
个车站时车上乘客数;Ui,j为第i辆车到达第j个车站时可以上车的人数;Di,j为第i辆车到达第j个车站的下车人数;D1、D2为研究时间段的起止时间;Q为快速公交车的固定承载能力;η为在研究时间段内的累计拥挤系数;βj为下车率;Pr表示概率测度;α1,α2,…,α5表示各约束条件在一定置信水平下的概率。
1.1 时间分析
(1)到站时间。第i辆车到达第j个车站的时刻tdi,j为第i 辆车离开第j-1个车站的时刻fi,j-1加上公交车在第j-1个车站和第j个车站之间的随机行驶时间Tj与第i-1辆车离开第j个车站的时间加上0.2 min(保证车辆先到先离开)相比较,取较大值,即:

(2)在站停车时间。第i辆车在第j个车站的停车时间Si,j为下车人数Di,j与上车人数Ui,j之和乘以人均上下车时间tud除以车门数n,再加上开关车门的时间tk,即:

(3)各站发车间隔。第j个车站的发车间隔hi,j等于第i辆车与第i-1辆车在第j个车站的离开时间差,即:

1.2 人数分析
(1)上车人数。在第j个车站上车的人数Ui,j为公交车的最大承载数减去到达第j个车站时的人数和第i-1辆车离开第j个车站至第i辆车到达第j个车站的时间段内到达车站的人数相比较,取较小值。由于fi,j为随机变量,故Ui,j也是随机的。公式如下:

(2)车上人数。第i辆车到达第j个车站时车上的人数qi,j等于第i辆车到达第j-1个车站时的人数qi,j-1加上在第j-1个车站上车的人数Ui,j-1,再减去在第j-1个车站下车的人数Di,j-1。由于Ui,j为随机变量,故qi,j也是随机的。公式如下:
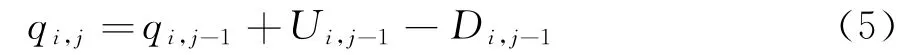
(3)下车人数。在第j个车站下车的人数Di,j与第i辆车到达第j个车站时的人数qi,j成正比,比例因子为βj,即:

(4)未上车人数。第i辆车离开第j个车站时未上车人数wi,j为第i-1辆车离开时未上车的人数加上第j个车站的发车间隔hi,j内到达的人数减去成功乘坐第i辆车的人数,并与零作比较,取较大值,即:

1.3 目标函数分析
目标函数是使乘客的等车时间成本、在车拥挤度及车辆运行时间成本在一定置信水平下为最小。
1.3.1 乘客的在站等车时间成本
乘客的在站等车时间成本等于乘客在第j个车站的到达率rj与相邻两辆公交车到达第j个车站的时间间隔fi,j-fi-1,j的乘积,再乘以等待时间的一半。若有未能上车的乘客,则再加上第i-1辆车离开时未上车的人数wi-1,j乘以第i辆车与第i-1辆车在第j个车站的发车间隔与等待第i-1辆车的时间之和。计算公式如下:

由于变量的随机性,可以使以置信度α1达到W1,则该目标函数可根据随机事件的意义改为:

1.3.2 乘客在车拥挤度
第i辆公交车的整体拥挤度η为第i辆车离开站台时车内实际人数qi,j与座位数m之差除以满载人数Q的1.2倍(最大乘客容量)与座位数m之差,并与零作比较,取较大值,然后进行累加。因为当比值小于零时,说明车内有空座位,此时均以零计。计算公式为:

同理,可以使ηi,j以置信度α2达到η1,则目标函数可根据随机事件的意义改为:

1.3.3 车辆运营成本
车辆运营时间成本C等于每次发车的成本乘
以该时间段内的发车次数,计算方法为:

使C 以置信度α3达到C1,则该目标函数可根据随机事件的意义改为:

1.3.4 约束条件
(1)乘客人数约束。快速公交车上的乘客数以一定置信水平不超过其本身的乘客容量,则有:

(2)乘客等待时间约束。在不确定的情况下,要使最大等待时间以一定的概率不超过最大能接受的等待时间,若超过这个时间,乘客就会不满,则有:

1.4 优化模型
根据以上对时间和人数的分析,建立优化快速公交发车间隔的随机机会约束规划模型如下:

式中:i=1,2,3,…,I;j=1,2,3,…,J。
式(16)表示综合目标值;式(17)表示乘客等待时间成本W至少以置信水平α1小于W1;式(18)表示乘客在车拥挤度η至少以置信水平α2小于η1;式(19)表示公交公司车辆运营时间成本C至少以置信水平α3小于C1;式(20)表示车上的人数qi,j至少以置信水平α4小于车辆容许载客量Q;式(21)表示每个乘客在任意车站的等待时间至少以置信水平α5小于最大可承受等待时间;式(22)表示保证优化后的发车间隔在规定值内;式(23)表示车辆离开第一个车站的时间要在研究时段内。
2 算法设计
根据随机机会约束规划模型的特点,考虑到微粒子群具有收敛速度较快、编程容易等优点,随机模拟具有对随机函数进行有效处理的优点,采用随机模拟与微粒子群相结合的混合智能算法对模型进行求解。算法步骤如下:
(1)对微粒群的各参数进行初始化。在粒子的可行域中依次产生和群体规模相等个数的随机数并对该随机数的可行性进行检验,得到初始可行微粒。
(2)计算粒子对应的综合目标值。
(3)将每个粒子的综合目标值和自身所经历的最好位置的综合目标值进行比较,若较好,则将其作为自身当前最好位置并保留。
(4)将每个粒子对应的最好综合目标值在全局进行比较,若较好,则将其作为全局当前最好位置并保留。
(5)根据微粒群算法的进化方程进化。
(6)对更新后的粒子再次利用随机模拟算法中的概率估算法计算Pr{gj(x,ξ)≤0,j=1,2,…,p},并检验粒子的可行性。若可行,则接受;否则,保持原位置不变。
(7)重复第2~6步直至一个预设的最大迭代数,得出最好的粒子和目标值。
(8)输出最好的粒子和对应的综合目标值作为最优解。
3 算例分析
下面以兰州市快速公交线路B1为例,对上述模型进行应用研究。研究时段为6:00—8:00。该条线路上共设15个车站,上行方向为刘家堡—兰州西站,下行方向为兰州西站—刘家堡。为了方便给出数据,根据上行方向顺序用数字1~15分别表示车站。快速公交车辆的额定载客量为60人,单位乘客上下车需2 s/人,α、β、λ分别取0.7、0.2、0.1。α1,…,α5均取0.9。根据历史数据得到研究时段内乘客到达率及站间行驶时间(见表1和表2)。

表1 乘客到达率和下车率

表2 相邻站点运行时间
运用MATLAB对模型进行编程求解,设置大小为30的粒子规模,令惯性因子为0.6、粒子的最大飞翔速度为0.5、加速常数c1和c2均为2。共迭代100次,得到当目标函数的综合目标值最小时,发车间隔为2.5 min。优化前后各项参数比较见表3和图1。
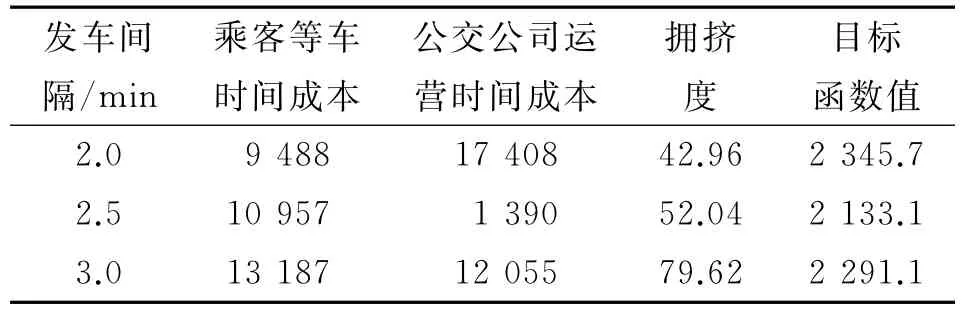
表3 优化前后各项参数比较

图1 综合目标值迭代图
由表3和图1可以看出:经过优化后,公交公司的运营成本有小幅度增加,但乘客等车时间成本和乘客在车拥挤度相比于优化前都有所降低,公交的服务质量得到提高,发挥了更好的社会效益。由此说明该模型及算法对快速公交发车间隔的确定具有较好的适用性。
4 结语
该文在考虑快速公交站间走行时间和乘客到达具有随机性的情况下,建立了使乘客等车时间最短、乘车拥挤度和车辆运营成本最低的多目标快速公交发车间隔优化模型,并设计了微粒群与随机模拟相结合的混合智能算法进行求解。兰州市快速公交B1的分析结果表明该模型及算法可用于确定快速公交发车间隔。但文中只对快速公交发车间隔的优化建立模型,对于随机条件的置信水平具体取值为多少时才能使快速公交发车间隔的确定更加合理还需进一步研究。
[1] 刘宝碇,赵瑞清.不确定规划及应用[M].北京:清华大学出版社,2003.
[2] Furth P G,Wilson N HM.Setting frequencies on bus routes:theory and practice[J].Transportation Research Record,1981,818.
[3] Ceder A,Tal O.Timetable synchronization for buses[A].Computer-Aided Transit Scheduling[C].Springer Berlin Heidelberg,1999.
[4] Parbo J,Nielsen O A,Prato C G.User perspectives in public transport timetable optimisation[J].Transportation Research Part C:Emerging Technologies,2014,48.
[5] 牛学勤,陈茜,王炜.城市公交线路调度发车频率优化模型[J].交通运输工程学报,2003,3(4).
[6] 宋瑞,赵航.基于机会约束的公交调度研究[J].数学的实践与认识,2005,35(1).
[7] 张东,李文权,郭士永,等.快速公交发车频率优化研究[J].武汉理工大学学报:交通科学与工程版,2015,39(2).
[8] 肖宁,曾建潮.基于随机模拟与PSO算法相结合的随机机会约束规划算法[J].计算机应用与软件,2009,26(4).
[9] Hassold S,Ceder A.Public transport vehicle scheduling featuring multiple vehicle types[J].Transportation Research Part B:Methodological,2014,67.
[10] 张红军,广晓平.随机环境下公交调度问题双层规划模型与算法[J].北京理工大学学报,2014,34(1).
[11] 杨晓光,安健.公交运行服务质量评价指标体系探讨[J].交通运输系统工程与信息,2010,10(4).
[12] 王琳,毛保华,张迅,等.基于遗传-模拟退火算法的公交发车间隔优化[J].公路与汽运,2013(3).
[13] 张琳琪.基于随机机会约束的公交实时调度研究[D].北京:北京交通大学,2009.
U491
A
1671-2668(2016)06-0021-04
2016-05-30
教育部人文社会科学研究项目(13XJC630017)

