机械弹性车轮疲劳寿命及其影响因素研究

张明杰, 赵又群, 杜现斌, 王强, 肖振

(南京航空航天大学 能源与动力学院，江苏 南京 210016)



机械弹性车轮疲劳寿命及其影响因素研究

张明杰, 赵又群, 杜现斌, 王强, 肖振

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

为提高机械弹性车轮的可靠性和耐久性，对其疲劳寿命进行了研究。结合机械弹性车轮的结构及承载方式，建立了疲劳试验的有限元模型；采用幅值、频率相同的正弦载荷和余弦载荷模拟车轮骨架载荷循环过程；基于Miner线性疲劳累积损伤理论进行疲劳寿命预测。分析表明：车轮骨架的疲劳破坏主要集中在弹性环组合卡与铰链组的连接部位，最小疲劳寿命为4.03×105次；随着铰链组个数、铰链组横截面积的增加，疲劳寿命呈非线性增加；随着实际负荷的增加，疲劳寿命呈下降趋势。

机械弹性车轮；疲劳试验；有限元模型；应力分析；Miner损伤理论；疲劳寿命

车轮是车辆的重要安全部件，是车辆与地面接触的唯一媒介，车轮的可靠性和耐久性直接关系到车辆的安全运行[1]。近年来，灌注式实心轮胎、内支撑体轮胎、内沉陷限制器轮胎等各种安全轮胎已逐步运用到安全防护性高的车辆中[2]。此外，安全车轮发展的新技术也层出不穷，如本田公司的防漏轮胎(TUFFUP TIRE)[3]、米其林公司的蜂窝板式车轮(TWEEL)[4]、负泊松比N-轮[5]。文献[6-8]探索了一种新型非充气式机械弹性安全车轮，并进行了一系列模型建立、径向刚度特性、力学特性等方面的理论和试验研究。为加速机械弹性车轮应用于某型越野车，在前期研究的基础上，本文进一步研究其疲劳寿命。结合机械弹性车轮的结构及承载方式，建立适用于机械弹性车轮疲劳寿命分析的有限元模型；基于Miner线性疲劳累积损伤理论，模拟动态弯曲疲劳试验对机械弹性车轮骨架进行疲劳寿命预测；探讨了疲劳寿命影响因素，为其设计优化和推广应用提供指导。

1 车轮结构及其承载方式

1.1 车轮结构

机械弹性车轮的总体结构如图1所示，主要由胎圈、轮毂、销轴、铰链组、弹性环、弹性环组合卡等部件构成，具体的组合关系如下：

1)将五束弹性环并列排放，利用等角度安装的12组弹性环组合卡将弹性环锁卡在一起，构成弹簧钢圈，如图2所示。

图1 机械弹性车轮外观Fig.1 Mechanical elastic wheel appearance

图2 机械弹性车轮骨架Fig.2 Mechanical elastic wheel skeleton

2)弹簧钢圈和轮毂对心安置，铰链组外端和弹性环组合卡连接，内端和轮毂连接。

3)弹簧钢圈外侧嵌入硫化的帘布层，其周围用橡胶层包裹，构成机械弹性车轮的胎圈。

1.2 车轮承载方式

车轮的承载方式有底部承载和顶部承载，机械弹性车轮承载方式类似于顶部承载，区别在于底部无受力[3](如图3)。

图3 机械弹性车轮的承载方式Fig.3 Loading mode of mechanical elastic wheel

机械弹性车轮在实际运转时，承受来自不平路面的载荷激励以及通过半轴传递的车重和弯矩。车轮胎圈承载变形，起到支撑作用，而铰链组则拉直或压弯变形。当铰链组受拉时，与二力杆相似，起到轴向传力作用；当铰链组受压时，则因绕铰接点转动弯曲变形而不承力。

2 车轮疲劳寿命研究的理论依据

车轮的疲劳寿命，可通过试验法和分析法来确定。试验法成本高、周期长、受偶然因素干扰，而分析法则可以预先进行疲劳分析和优化，节约成本并缩短车轮推向市场的时间。

2.1 车轮动态弯曲疲劳试验

车轮动态弯曲疲劳试验是国际上通行的、标准的试验方法[9-11]，国家标准GB/T 5334-2005 《乘用车车轮性能要求和试验方法》规定动态弯曲疲劳试验弯矩计算公式为

M=(μR+d)FvS

(1)

式中：μ是轮胎与路面间的设定摩擦系数，R是轮胎静负荷半径，d是车轮内偏距或外偏距，Fv是车轮或汽车制造厂规定的车轮上的最大垂直静负荷或车轮的额定负荷，S是强化试验系数。

2.2 疲劳累积损伤理论

疲劳累积损伤理论可归纳为以下三类：线性疲劳累积损伤理论、修正的线性疲劳累积损伤理论和非线性疲劳累积损伤理论[12]。工程上广泛使用的是Miner线性疲劳累积损伤理论，其法则为

(2)

式中：D为总疲劳损伤，ni为各应变水平下的循环次数，Ni为疲劳寿命。

3 车轮有限元模型的建立

3.1 模型假设条件

为提高计算效率，在保证结果精度的前提下，对机械弹性车轮有限元模型进行了适度简化：

1)不考虑连接和接触部位的摩擦作用，按无摩擦接触处理；

2)忽略销轴结构，不研究其疲劳寿命，用转动副模拟其运动特性；

3)胎圈结构为非线性材料，特性复杂，不考虑其对机械弹性车轮骨架应力历程的影响；

4)假设所有材料属性为各向同性，车轮骨架结构相对轮心完全对称；

5)不考虑温度变化对机械弹性车轮骨架各项性能的影响。

3.2 材料特性及单元类型

车轮骨架材料采用7075-T651铝合金[13]，其密度为2 770 kg/m3，抗拉强度为580 MPa，屈服强度为σs=570 MPa，选取所选用铝合金材料的安全系数为2，则许用应力[σ]=σs/2=285 MPa，杨氏模量为71 GPa，泊松比为0.33。车轮骨架采用Solid186和Solid187单元，接触面处采用Conta174和Targe170单元。

3.3 网格划分

为避免出现畸形单元，模型中主要采用六面体和扫略方法进行网格划分，得到了较为工整的网格，以加强收敛性和计算精度。试验时关注铰链组和轮毂的应力分布，该部分网格划分较细，而其他部分网格较粗，对于加载轴，只利用它施加载荷，对其应力分布不感兴趣，故将其设置为刚体。该有限元简化模型划分网格后，模型单元数为50 680，节点数为40 512，网格划分效果如图4所示。

图4 机械弹性车轮有限元模型Fig.4 Finite element model of mechanical elastic wheel

3.4 基于动态疲劳弯曲试验的边界条件

车轮可在一固定不动的弯矩作用下旋转，或者车轮固定不动，而承受一个旋转的弯矩，试验弯矩由式(1)确定。

为了对车轮骨架施加旋转弯矩，可在加载轴末端施加大小不变，但方向随时间而改变的载荷[12-13]。机械弹性车轮载荷计算参数为：R=0.815 m，d=0.040 m，Fv=10 kN，S=1.6，加载轴长度L=0.8 m，取μ=0.7。求得弯矩M=

9.768kN·m，试验加载载荷F=M/L=1.221 kN。该载荷可分解相互垂直的两个力，分别为Fx=Fsin(ωt)和Fy=Fcos(ωt)，其中ω为由实际试验转速求得的角速度，t为时间变量。图5为动态疲劳弯曲试验的载荷历程曲线，图中橫轴表示车速为60 km/h时车轮旋转一周所需要的时间。

图5 动态疲劳弯曲试验的载荷历程曲线Fig.5 Load history curve of dynamic fatigue bending test

具体地，边界条件为固定车轮骨架弹性环组合卡的外端面，通过螺栓连接车轮轮毂和加载轴法兰盘，同时在加载轴末端面的中心节点施加相互垂直的载荷：Fx=1.221sin(40.90t)和Fy=1.221cos(40.90t)。

4 有限元模型的结果分析

4.1 动态疲劳弯曲试验仿真结果分析

1)应力分析

受模拟旋转载荷的影响，应力云图发生周期变化。图6为某时刻的应力分布图，在加载轴法兰盘与轮毂的连接处附近产生一定的应力集中，同时轮毂边缘销轴孔附近应力集中也很明显。在铰链组第一节铰链内侧产生最大应力，最大应力值为270.51 MPa。最大应力小于材料的许用应力，但可推断此处最易发生疲劳破坏。

图6 动态疲劳弯曲试验某时刻的应力分布图Fig.6 The stress distribution diagram of dynamic fatigue bending test at a certain time

为了研究车轮在动态弯曲疲劳试验仿真过程中所承受的应力循环情况和疲劳破坏的机理，提取车轮上应力水平较高的危险点的应力状态进行分析。图7表示危险点应力随加载角度的变化情况，即动态弯曲疲劳试验中试验弯矩旋转一周，危险点的应力变化情况。可以看出该危险点所承受的是非对称应力循环。

图7 危险点应力随加载角度的变化情况Fig.7 Variation of the stress at dangerous point with loading angle

2)疲劳寿命预测

基于Miner线性疲劳累积损伤理论并采用Goodman修正模型，计算出疲劳寿命值与疲劳破坏的位置。动态疲劳弯曲试验的寿命分布情况如图8所示，最小疲劳寿命为4.03×105次，在铰链组第一节铰链内侧最先发生疲劳破坏，此结果与车轮骨架应力分布情况相符。

图8 动态疲劳弯曲试验的疲劳寿命分布图Fig.8 Fatigue life distribution diagram of dynamic fatigue bending test

4.2 疲劳寿命的影响因素分析

车轮的疲劳寿命对车辆的可靠性影响重大。由动态弯曲疲劳试验的应力分析可知，车轮疲劳寿命主要取决于铰链组结构特征和车辆运行工况。因此基于车轮有限元模型对铰链组个数、铰链组横截面积和车轮实际负荷等变量进行参数化分析，得出它们与车轮骨架疲劳寿命之间的变化规律。

利用有限元模型分别计算了车轮骨架在90%、100%、120%、140%的额定负荷下，铰链组个数、横截面积对车轮疲劳寿命的影响。

铰链组横截面积为288 mm2，铰链组个数对疲劳寿命的影响如图9所示。由图9可知，随着铰链组个数的增加，车轮骨架的疲劳寿命值呈非线性增加。铰链组个数为6时，车轮骨架在100%的额定负荷下即发生破坏，可见铰链组个数太少时车轮骨架易发生破坏。

铰链组个数为12，铰链组横截面积对疲劳寿命的影响如图10所示。由图10可知，随着铰链组横截面积的增大，车轮骨架疲劳寿命值呈非线性增加。铰链组横截面积从288 mm2增加到408 mm2，车轮骨架疲劳寿命值缓慢增加，在铰链组第一节铰链内侧最先发生疲劳破坏；当铰链组横截面积增加到432 mm2时，轮毂中心附近的螺栓孔先发生破坏。

由图9和图10可知，随着车轮的实际负荷增加，车轮骨架的疲劳寿命呈下降趋势；相对于增大铰链组横截面积，增加铰链组个数提升车轮骨架疲劳寿命更明显。

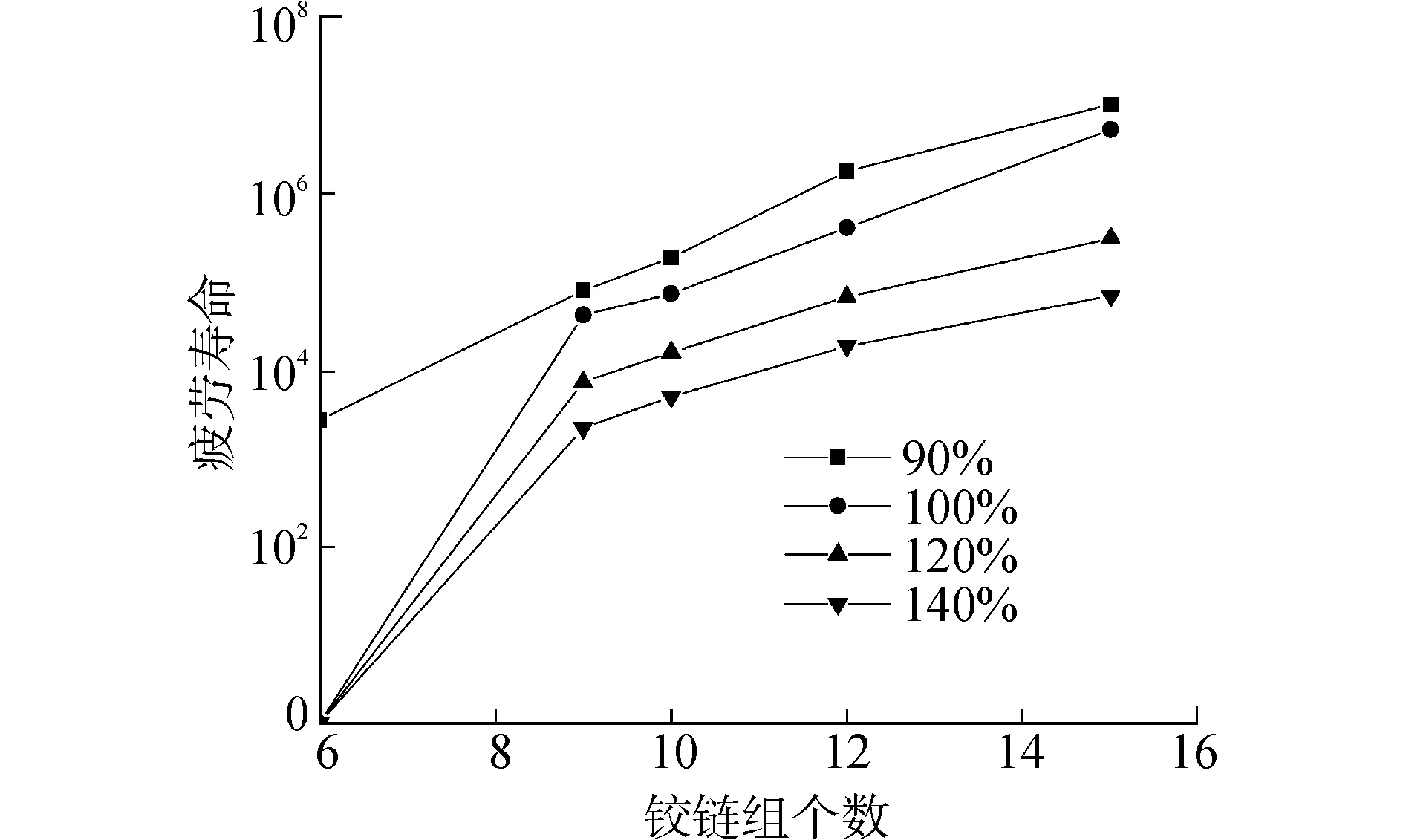
图9 铰链组个数对疲劳寿命的影响Fig.9 Influence of hinge number on fatigue life

图10 铰链组横截面积对疲劳寿命的影响Fig.10 Influence of cross section area of hinge group on fatigue life

5 结论

基于Miner线性疲劳累积损伤理论和车轮动态弯曲疲劳试验对机械弹性车轮的疲劳寿命进行了预测和影响因素分析。

1)车轮动态弯曲疲劳试验中，机械弹性车轮骨架结构的危险点承受非对称应力循环，在铰链组第一节铰链内侧产生最大应力。

2)机械弹性车轮的疲劳寿命与铰链组的结构特征和车辆运行工况有关。随着铰链组个数、铰链组横截面积的增加，机械弹性车轮骨架的疲劳寿命呈非线性增加，且适当增加铰链组个数能更显著的提高车轮骨架疲劳寿命；随着实际负荷的增加，机械弹性车轮骨架的疲劳寿命呈下降趋势。

[1]辛振祥, 邓涛, 王伟. 现代轮胎结构设计[M]. 北京：化学工业出版社, 2011: 1-2.

[2]岳红旭, 赵又群. 一种新型安全车轮的非线性有限元分析[J]. 中国机械工程, 2012, 23(11): 1380-1385. YUE Hongxu, ZHAO Youqun. Nonlinear finite element analysis of a new safety wheel[J]. China mechanical engineering, 2012, 23(11): 1380-1385.

[3]ASANUMA N, KAWAI M, TAKAHASHI A, et al. Intelligent technologies of ASV (The research and development of ASV-2 in Honda)[C]//Proceedings of 7th World Congress on Intelligent Systems. Turin: ERTICO, 2000: 1-12.

[4]MA Jianfeng, KOLLA A, SUMMERS J D, et al. Numerical simulation of new generation non-pneumatic tire (TWEELTM) and sand[C]//ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. San Diego: American Society of Mechanical Engineers, 2009: 123-130.

[5]马正东. 基于负泊松比结构的超轻重量非充气轮胎结构: 中国, 201110401962.4[P]. 2012-07-04.

[6]臧利国, 赵又群, 李波, 等. 非充气机械弹性车轮静态径向刚度特性研究[J]. 兵工学报, 2015, 36(2): 355-362. ZANG Liguo, ZHAO Youqun, LI Bo, et al. Static radical stiffness characteristics of non-pneumatic mechanical elastic wheel[J]. Acta armamentarii, 2015, 36(2): 355-362.

[7]臧利国, 赵又群, 李波, 等. 机械弹性车轮结构参数对牵引性能的影响[J]. 哈尔滨工程大学学报, 2014, 35(11): 1415-1421. ZANG Liguo, ZHAO Youqun, LI Bo, et al. Influence of mechanical elastic wheel configuration on traction performance[J]. Journal of Harbin engineering university, 2014, 35(11): 1415-1421.

[8]李波, 赵又群, 陈月乔, 等. 弹性车轮纵向力刷子模型分析[J]. 哈尔滨工程大学学报, 2015, 36(5): 662-665. LI Bo, ZHAO Youqun, CHEN Yueqiao, et al. Longitudinal force analysis for an elastic wheel based on the brush model[J]. Journal of Harbin engineering university, 2015, 36(5): 662-665.

[9]KOCABICAK U, FIRAT M. Numerical analysis of wheel cornering fatigue tests[J]. Engineering failure analysis, 2001, 8(4):339-354.

[10]RAJU P R, SATYANARYANA B, RAMJI K, et al. Evaluation of fatigue life of aluminium alloy wheels under bending loads[J]. Fatigue & fracture of engineering materials & structures, 2009, 32(2): 119-126.

[11]WANG Liangmo, CHEN Yufa, WANG Chenzhi, et al. Fatigue life analysis of aluminum wheels by simulation of rotary fatigue test[J]. Strojniski vestnik-journal of mechanical engineering, 2011, 57(1): 31-39.

[12]姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2003: 75-92.

[13]韩剑, 戴起勋, 赵玉涛, 等. 7075-T651铝合金疲劳特性研究[J]. 航空材料学报, 2010, 30(4): 92-96. HAN Jian, DAI Qixun, ZHAO Yutao, et al. Study on fatigue performance of 7075-T651 aluminum alloys[J]. Journal of aeronautical materials, 2010, 30(4): 92-96.

[14]闫胜昝, 童水光, 张响, 等. 汽车车轮弯曲疲劳试验分析研究[J]. 机械强度, 2008, 30(4): 687-691. YAN Shengzan, TONG Shuiguang, ZHANG Xiang, et al. Analysis study on bending fatigue test of automobile wheels[J]. Journal of mechanical strength, 2008, 30(4): 687-691.

[15]WANG Xiaofeng, ZHANG Xiaoge. Simulation of dynamic cornering fatigue test of a steel passenger car wheel[J]. International journal of fatigue, 2010, 32(2): 434-442.

Fatigue life and influencing factors of a mechanical elastic wheel

ZHANG Mingjie, ZHAO Youqun, DU Xianbin, WANG Qiang, XIAO Zhen

(College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

In this paper, the fatigue life of a mechanical elastic wheel is studied to improve its reliability and durability. The finite element model of the fatigue tests is established by combining the structure and the loading mode of a mechanical elastic wheel. Sine and cosine loads with the same amplitude and frequency are applied to simulate a load cycle process of the wheel skeleton. The fatigue life is predicted on the basis of Miner linear fatigue cumulative damage theory. The analysis results show that the fatigue failures of the wheel skeleton is mainly centered on the connection of the flexible ring composite clip and hinge group. The minimum fatigue life is 4.03 × 105times. The fatigue life nonlinearly increases as the number and cross-section area of the hinge group increase. The fatigue life decreases as the actual load increases.

mechanical elastic wheel; fatigue tests; finite element model; stress analysis; Miner damage theory; fatigue life

2015-09-09.

日期：2016-09-28.

总装探索研究项目(NHA13002); 江苏省普通高校研究生科研创新计划项目(KYLX_0241).

张明杰(1990-), 男, 硕士研究生; 赵又群(1968-), 男, 教授,博士生导师.

赵又群, E-mail: yqzhao@nuaa.edu.cn.

10.11990/jheu.201509026

U463.3

A

1006-7043(2016) 11-1560-05

张明杰, 赵又群, 杜现斌, 等. 机械弹性车轮疲劳寿命及其影响因素研究[J]. 哈尔滨工程大学学报, 2016, 37(11): 1560-1564. ZHANG Mingjie, ZHAO Youqun, DU Xianbin, et al. Fatigue life and influencing factors of a mechanical elastic wheel[J]. Journal of Harbin Engineering University, 2016, 37(11): 1560-1564.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160928.1419.040.html