基于响应面方法的叶栅摆动装置有限元模型修正

麻越垠， 陈万华，2， 王元兴，2， 谢 强， 李远莉

(1. 中国空气动力研究与发展中心,四川 绵阳 621000； 2. 空气动力学国家重点实验室,四川 绵阳 621000)



基于响应面方法的叶栅摆动装置有限元模型修正

麻越垠1， 陈万华1，2， 王元兴1，2， 谢 强1， 李远莉1

(1. 中国空气动力研究与发展中心,四川 绵阳 621000； 2. 空气动力学国家重点实验室,四川 绵阳 621000)

为提高叶栅摆动装置模态分析与模态试验的相关性，使用响应面方法对有限元模型多个参数进行优化，实现模型修正。首先使用有限元模型进行模态分析，提取整体模态；其次，采用移动传感器方法对大型装配体进行整体模态试验，通过模态判据准则检验模态试验结果、模态参与因子确定主要整体模态；再次，基于有限元模型误差分析，确定对主要部件分别采用不同材料修正参数，通过中心复合试验设计确定样本空间，使用多目标响应面方法对样本进行回归分析，在回归分析的响应面内对待修正参数进行非线性约束优化，得到最优解；最后，使用修正参数重新进行模态分析实现模型确认，并进行动力学计算，与实际测试结果对比。结果表明，修正后的模态分析与模态试验结果相关性提高，前三阶整体模态频率误差均值由9.71%减小至0.73%，振型相关性由0.74提升至0.89。

模型修正；响应面方法；模态试验；模态分析；叶栅摆动装置

有限元法是目前工程上广泛采用的结构建模方法，精确的有限元模型对于结构动态响应预测以及设计起到至关重要的作用[1]。在建立有限元模型时，由于边界条件的近似、材料实际参数的不确定等原因使得建立的模型并不能准确反映真实结构的动力学特性。模型修正技术就是为解决上述问题而发展的一门涉及模态分析、矩阵理论、优化理论、结构动特性计算和试验技术等多个学科领域的一门综合技术，其按照修正对象的不同可以将其分为矩阵型和参数型两大类[2]。常用的基于灵敏度分析的模型修正技术在国内外均有相关研究，由于灵敏度分析的迭代计算，增加很多工作量，对于复杂结构，当修正参数增加时，计算量相应也会变得更大。响应面方法(RSM)是一种数理统计学技术，目的在于改善和优化输入与响应过程的数据。响应面方法实施起来相对容易，相对于其他修正方法提高了计算的效率，并且避免了结构灵敏度分析过程[3]，基于响应面方法的模型修正技术研究和应用正逐渐热门起来，2013年，李万德开展基于响应面的自锚式悬索桥有限元模型修正，取得良好效果[4]；2014年，苏忠亭针对某火炮车体和身管开展基于模态试验的模型修正，以模态频率和阵型的方差为优化目标函数，同时提高了频率和阵型的相关性[5-6]。基于响应面方法的模型修正技术的概念表述为：在变量的设计空间内，釆用回归分析法对样本点处的响应值或试验值拟合，得到模拟真实极限状态曲面的响应面，在参数设计空间内进行响应面模型修正和验证[7]。

某叶栅摆动装置在实际使用中受周期风载影响较大，为准确预测其动态特性，需要精确的有限元计算模型。使用ABAQUS进行模态分析；采用MIMO法开展模态试验；在有限元误差分析基础上，确定待修正参数；使用中心复合设计确定样本空间，使用多目标响应面方法对样本进行回归分析，在回归分析的响应面内对修正参数进行非线性约束优化，得到最优解；使用修正后的参数进行模型确认。

1 有限元模态分析

经过合理简化，在ABAQUS中建立叶栅摆动装置有限元模型，如图1所示，叶栅摆动装置主要由底座、支撑梁、支撑架和连接杆组成，分别对各部件划分网格，然后组装成装配体， 各部件之间根据实际连接等效

为绑定约束或铰链连接，底座与地面固定连接。选择六面体8节点缩减积分单元(C3D8R)为分析单元，装配体网格划分结果总计134 567个单元，219 396个节点。所有材料均为普通碳钢，弹性模量E=2.1e11 Pa，泊松比μ=0.3，密度ρ=7 800 kg/m3。

忽略阻尼，对上述装配体进行模态分析，计算25 Hz以内的模态频率。实际关注的是装置的整体动力学特性，由于连接杆刚度相对整体刚度较低，存在局部模态，所以忽略局部模态，提取前5阶整体模态，表1为前5阶整体模态频率，对应的阵型如图2所示。

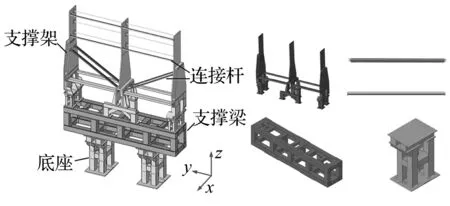
图1 有限元分析模型Fig.1 Finite element model表1 装配体前5阶整体模态频率Tab.1 The first five frequencies of the whole assembly

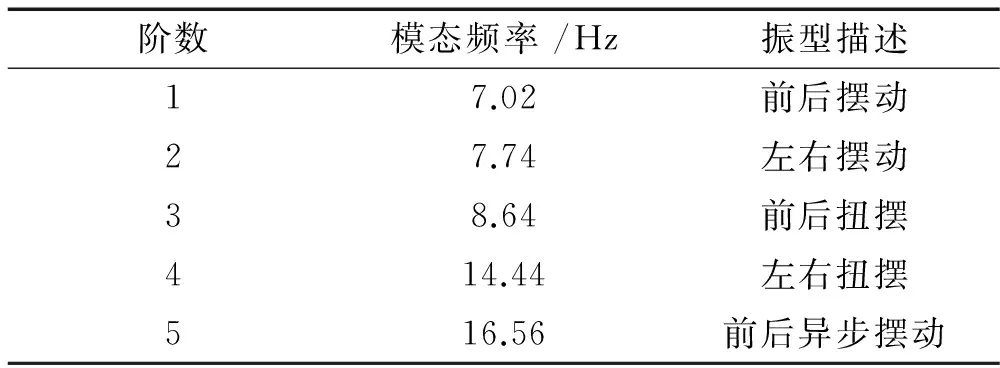
阶数模态频率/Hz振型描述17.02前后摆动27.74左右摆动38.64前后扭摆414.44左右扭摆516.56前后异步摆动

图2 模态分析前5阶整体阵型Fig.2 The first five modal shapes of the whole assembly

2 模态试验

模态试验坐标轴规定如图1所示，由有限元模态分析可知，模态主要集中在X向和Y向，考虑到装置整体为竖直悬臂梁式结构，选择支撑架右侧顶部为激励点，采用锤击法测试，锤击方向为X向和Y向。

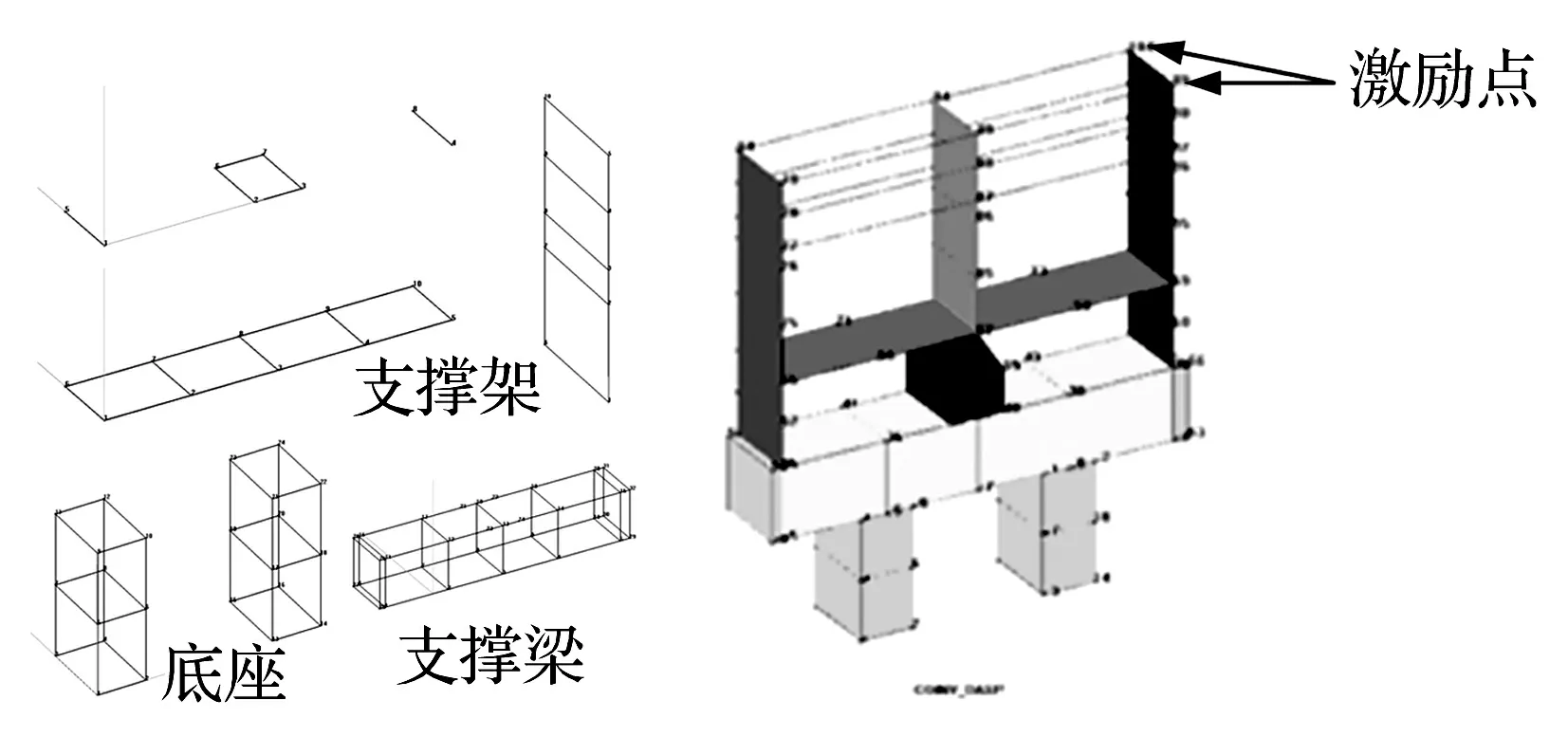
图3 模态试验建模Fig.3 Experimental model

为了完整捕捉整体振型，需要较多的测点，采用移动传感器的测试方式解决传感器不足的问题，分别测试各部件的模态，最后合成整体模态，在软件中根据测点建立各个部件的模态试验结构，装配后形成整体模态试验模型[8-10]，如图3所示，图中的点为测点布置位置。图3中测点有104个，每个测点测试X向和Y向两个自由度，激励点为图3中的99和104号测点，每个激励点分别敲击两个方向，单个方向激励3次。

响应点采样频率80 Hz，激励点采样频率为2 560 Hz，采用变时基采样，变时基倍数为32，单次激励和响应点采样结果如图4所示。单次激励峰值部分采样点约为47，大于推荐值20，单个测点单个自由度3次激励采样时间约为38 s，各次激励均已充分衰减。

图4 单次激励和响应Fig.4 One hammering and response

通过对测试数据进行模态分析，提取整体结构前5阶模态特性，前5阶固有频率如表2所示，图5为模态试验前5阶整体振型。

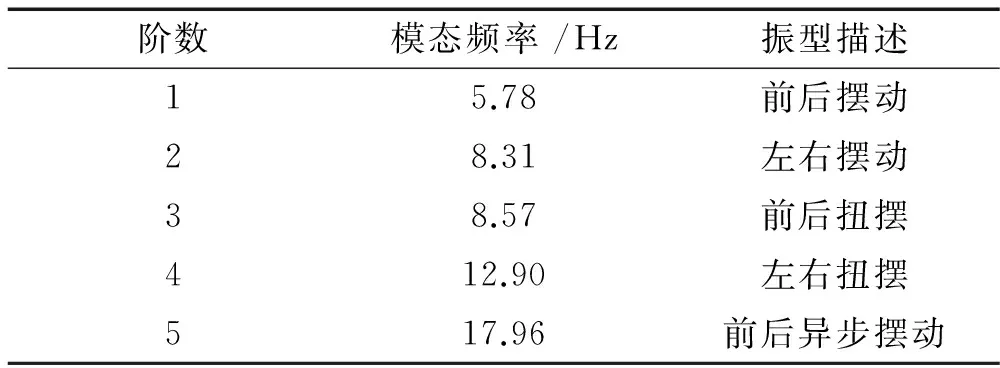
表2 模态试验前5阶整体模态频率Tab.2 The first five experimental modal frequencies

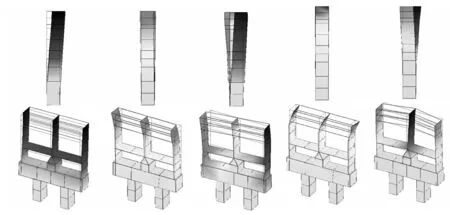
图5 模态试验前5阶整体振型Fig.5 The first five experimental modal shapes

对上述5阶模态分析结果进行验证，采用模态判定准则MAC值来比较不同阶的振型，衡量各阶的相关性，两个模态振型向量{Ψ}r和{Ψ}s之间的模态判定准则定义为：

MAC({Ψ}r,{Ψ}s)=

(1)

如果{Ψ}r和{Ψ}s是同一物理振型的估计，那么模态判定准则应该接近于1，如果{Ψ}r和{Ψ}s是不同物理振型的估计，那么模态判定准则应该很低。模态判定准则如图6所示，由图可知，模态判定准则对角线占优，试验结果可信。

图6 模态判定准则Fig.6 Modal assurance criterion

模态参与因子用来研究各模态的相对重要性以及所选输入自由度的有效性，输入n对模态r的参与因子MPnr计算公式为：

(2)

式中:x为输出自由度；Axnr为输出x、输入n、模态r的留数。

图7为本次试验的模态参与因子，可以看出，前3阶模态对整体的参与因子分别为29.2%、32.2%和29.7%，占整体模态的91.1%。图8为试验振型与模态分析振型的相关性分析，前3阶整体模态频率试验值与计算值的比较见表3。

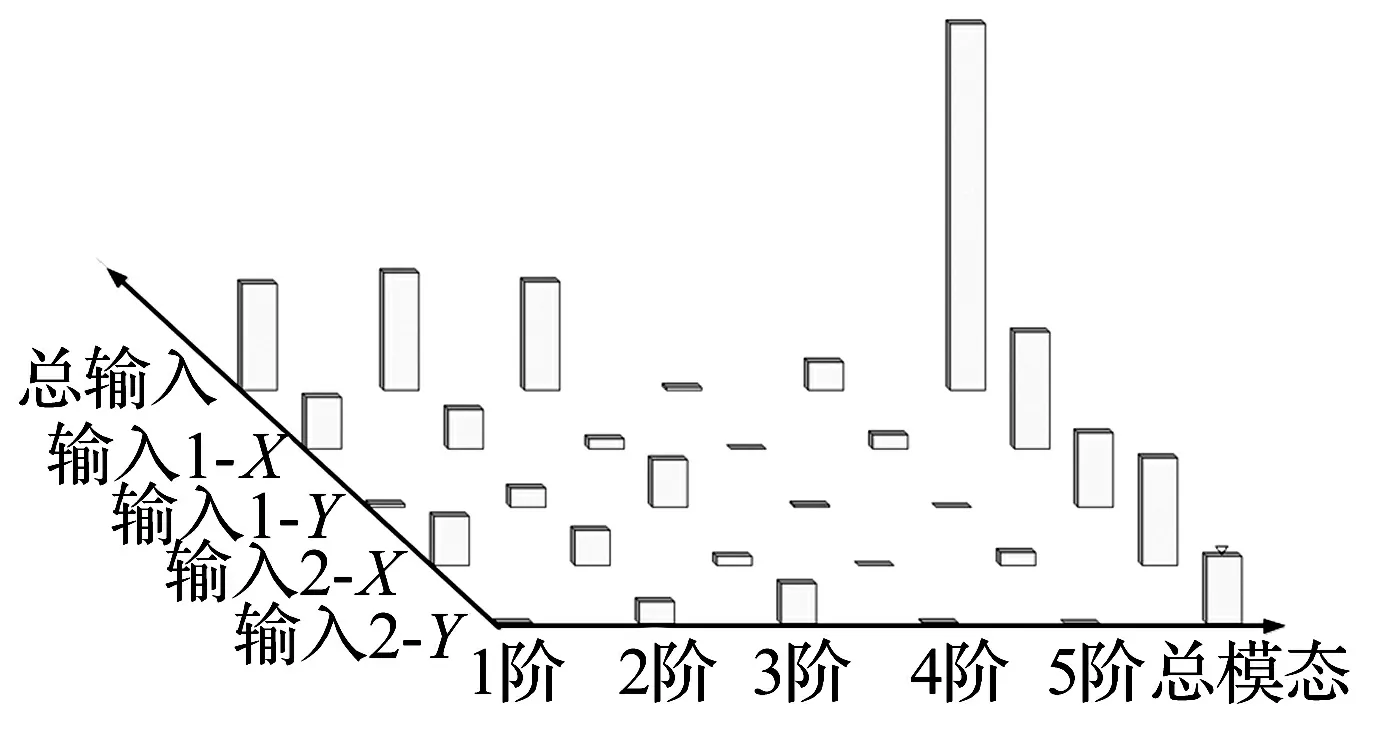
图7 模态参与因子Fig.7 Modal participation factor

图8 模态分析与模态试验振型相关性Fig.8 Modal shape MAC between FE and experimental model表3 整体模态频率试验值与计算值对比Tab.3 Modal frequencies comparison of test value and calculated value

阶数试验值/Hz计算值/Hz误差/%15.787.0221.4528.317.746.8638.578.640.82

3 多变量有限元模型修正

3.1 有限元误差分析及参数选取

有限元模态分析使用的是实际结构的简化模型，对多个驱动部件和零部件进行了省略，同时，各部件之间的螺栓连接等简化为绑定约束，这必然导致计算模型质量矩阵、刚度矩阵与实际存在一定误差。根据有限元模型修正经验，通常采用的修正参数是弹性模量和密度，一般的做法是设定整体质量采用统一的材料，以减少变量值，提高优化效率，但同时也会影响优化最终目标值。本次有限元分析模型在支撑梁上主要简化了电机等传动设备，其主要影响质量矩阵；在支撑架上主要简化了叶栅等装置，其对质量矩阵影响远没有传动设备大；底座主要简化了连接关系，对刚度矩阵影响较大。结合本次分析结构复杂，质量、刚度简化不均的特点，使用模型修正经验选择材料的弹性模量E和密度ρ为修正目标，对主要部件(底座、支撑梁和支撑架)使用不同的材料，因此，修正目标共有6个，采用中心复合试验设计，各修正目标各有5个水平，即6目标5水平中心复合试验设计，共需要45个样本，修正目标水平如表4所示。

表4 修正目标水平表Tab.4 Modal updating parameters and level

3.2 响应面模型的建立

常见的响应面模型有完全和不完全多项式模型、克里格模型、BP神经网络模型和径向基函数等模型，完全多项式模型公式为

(3)

式中:xi(i=1,…,N)是预测变量，对应有限元分析中的待修正的材料属性；y(x)为预测值，对应的是模态频率。采用式(3)中的二次完全多项式模型，回归分析后产生的响应面模型为：

(4)

根据上述求解前三阶整体模态频率的响应面模型，由式(4)可知，每个频率响应面模型中含有28个系数，如表5所示。

表5 响应面模型系数 (×10-3)Tab.5 Parameters of RSM (×10-3)

3.3 多目标优化与确认

使用MATLAB多元非线性规划函数fmincon对上述6个材料参数进行优化，优化的目标函数为:

(5)

式中:f(i)为响应面预测频率值，fi模态试验值。

函数优化过程如图9所示，经过12次运算后，函数收敛在容差范围内。经过优化，各部件的材料参数修正结果为：支撑架：弹性模量E=2.192e11 Pa，密度ρ=6 967.4 kg/m3；支撑梁：弹性模量E=1.876e11 Pa，密度ρ=7 669.5 kg/m3；底座：弹性模量E=1.973e11 Pa，密度ρ=7 635.4 kg/m3。

图9 优化过程Fig.9 Optimization process

使用修正后的材料参数进行模态分析，前3阶整体模态如图10所示；修正后有限元振型与试验振型的相关性分析如图11所示；修正后的前3阶整体有限元模态频率与试验模态频率对比见表6，修正后有限元模态振型和试验模态振型相关性对比见表7。

由图10、图11、表6和表7可以看出，模型修正后，有限元前3阶固有频率与模态试验频率最大误差为1.06%，均值为0.73%，对动力学影响最大的一阶频率误差降低至0.17%；修正后的振型相关性也有了明显提升，其中一阶整体振型相关性提高至0.91，相关性均值提高至0.893，说明修正后有限元模型振型与实际更为吻合。

图10 模型修正后装置前3阶整体模态Fig.10 The first three modes of modal updating

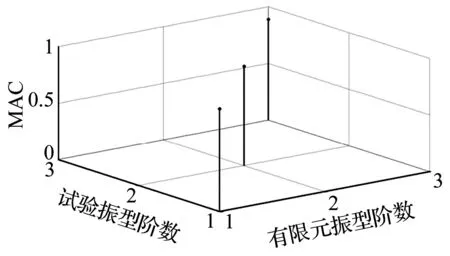
图11 修正后有限元振型与试验振型相关性Fig.11 Modal shape MAC between updated model and experimental model表6 整体模态频率试验值与修正值对比Tab.6 Modal frequencies comparison of test value and updated value

阶数试验值/Hz修正值/Hz误差/%15.785.770.1728.318.390.9638.578.481.06

表7 模型修正后模态分析与试验振型相关性对比Tab.7 Modal shape MAC comparison of test value and updated value

4 模型应用

使用未修正和修正后的模型进行有限元动力学计算，载荷输入为实际测试载荷，对比计算和实际测试的同一点的振动加速度频谱，如图12所示。可以看出，未修正的模型一阶频率在7 Hz左右，修正后的模型，一阶频率为5.8左右，二阶频率在8.3左右，与模态测试结果基本一致；并且修正后模型动力学计算频谱与实际测试频谱吻合度很高。

图12 修正前后装置振动频谱对比Fig.12 Comparison of frequency spectrums

5 结 论

本文使用响应面法，在模态试验基础上，对叶栅摆动装置有限元模型进行修正，从有限元模型建立过程中简化出发，确定主要部件的材料属性为修正变量，修正方法采用响应面法。模态测试前三阶模态频率分别为5.78 Hz、8.31 Hz和8.57 Hz，修正后，装置的前三阶计算模态频率分别由7.02 Hz、7.74 Hz、8.64 Hz更新为5.77 Hz、8.39 Hz和8.48 Hz，模态试验和有限元计算的前三阶整体模态频率误差均值由9.71%减小至0.73%，其中一阶频率误差从21.45%降至0.17%。修正后模型一阶整体振型相关性由0.68提高至0.91，前三阶振型相关性均值提高至0.893。最后将修正后的模型动力学计算结果与实际测试结果对比，两者振动情况吻合度比修正前有明显提高，表明响应面法对该装置有限元模型修正结果可信，修正后的模型与实际模型动力学特性更符合。

[1] 费庆国, 张令弥, 李爱群, 等. 基于统计分析技术的有限元模型修正研究[J]. 振动与冲击, 2005, 24(3): 23-26. FEI Qingguo, ZHANG Lingmi, LI Aiqun, et al. Finite element model updating using statistics analysis [J]. Journal of Vibration and Shock, 2005, 24(3): 23-26.

[2] 李佰灵, 荣克林. 基于响应面方法的多目标有限元模型修正技术研究[J]. 强度与环境, 2010, 37(4): 13-21. LI Bailing, RONG Kelin. Study of finite element model updating for multi-objective based on the response surface method [J]. Structure & Environment Engineering, 2010, 37(4): 13-21.

[3] 朱宏平, 徐斌, 黄玉盈. 结构动力模型修正方法的比较研究及评估[J]. 力学进展, 2002, 32(4): 513-524. ZHU Hongping, XU Bin, HUANG Yuying. Comparison and evaluation of analytical approaches to structural dynamic model correction [J]. Advances in Mechanics,2002, 32(4): 513-524.

[4] 李万德. 基于响应面的自锚式悬索桥有限元模型修正[D]. 哈尔滨：东北林业大学, 2013.

[5] 苏忠亭, 徐达, 杨明华. 基于模态试验的某火炮身管有限元模型修正[J]. 振动与冲击, 2012, 31(24): 54-59. SU Zhongting, XU Da, YANG Minghua. Finite-element model updating for a gun barrel based on modal test [J]. Journal of Vibration and Shock, 2012, 31(24): 54-59.[6] 苏忠亭, 徐达, 李晓伟. 步兵战车车体结构有限元模型修正[J]. 振动、测试与诊断， 2014, 34(6): 1148-1153. SU Zhongting, XU Da, LI Xiaowei. Finite-element model updating for infantry combat vehicle car-body [J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(6): 1148-1153.

[7] 况志强. 基于模态试验及模型修正技术的龙洗研究[D]. 北京：北京邮电大学, 2011.

[8] 李晓东, 刘凡, 刘继军. 复杂框架结构模态试验准备及设计技术[J]. 强度与环境. 2013, 40(4): 27-30. LI Xiaodong, LIU Fan, LIU Jijun. Test design and preparation techniques of modal test for complicated frame structure [J]. Structure & Environment Engineering, 2013, 40(4): 27-30.

[9] 张喜清, 项昌乐, 刘辉. 基于预试验分析的复杂箱体结构试验模态研究[J]. 振动与冲击, 2011, 30(4): 109-112. ZHANG Xiqing，XIANG Changle，LIU Hui. Modal testing study on a complicated housing structure based on pre-test analysis [J]. Journal of Vibration and Shock, 2011, 30(4): 109-112.

[10] 刘渊. 结构振动模态测试优化技术的研究及其应用[D]. 南京：南京航空航天大学, 2011.

Finite element model updating of a blade swing mechanism based on response surface method

MA Yueyin1, CHEN Wanhua1,2, WANG Yuanxing1,2, XIE Qiang1, LI Yuanli1

(1. China Aerodynamics Research and Development Center, Mianyang 621000, China；2. State Key Laboratory of Aerodynamics, Mianyang 621000, China)

In order to improve the correlation between the results of modal analysis and modal test for a blade swing mechanism, a multiple parameters optimization was brought into updating the finite element model by using the response surface method. The overall modal parameters of the structure were extracted by the numerical modal analysis. And for this large assembly, a modal test was also developed by moving the sensor other than the hammer. The assurance criterion and the mode participation factor were made in use respectively to validate the test results and to confirm the main modes. Based on the finite element model error analysis, the model updating was carried out, using different material modification parameter at different part of the structure. The sample space was calculated and determined by the central composite test design, and the regression analysis on the samples was achieved by use of the multiple objectives response surface method, where the model updating targets were optimized. Finally, the modified parameters were applied in a new modal analysis to validate the accuracy of the updated model. On this basis, the dynamic simulation results were compared with the actual test results. The results show that the correlation between the results of modal test and updated modal analysis is improved, the average frequency error of the first three modes is reduced from 9.71% to 0.73%, and the modal shape MAC is improved from 0.74 to 0.89.

model updating; response surface method; modal test; modal analysis; blade swing mechanism

军内科研计划项目

2015-05-25 修改稿收到日期：2015-08-28

麻越垠 男，硕士，工程师，1987年12月生

陈万华 男，硕士，副研究员，1975年6月生

TH113.1

A

10.13465/j.cnki.jvs.2016.22.035