吊舱发电用涵道式冲压涡轮优化设计

叶国祥+陆启航+张大林

摘要： 冲压涡轮作为吊舱发电系统的动力部件， 其性能直接影响整个系统的工作性能。 采用11参数法对冲压涡轮二维叶型进行造型， 并利用后缘积叠进行三维成型生成冲压涡轮。 应用Fluent对其进行数值计算， 在保证涡轮质量流量及输出功率不降低的情况下， 以涡轮损失系数为目标函数， 基于试验设计和Kriging模型对冲压涡轮叶片数及转子几何外形进行气动优化。 研究结果表明： 基于试验设计和Kriging模型的优化策略能以较少的试验次数获得良好的优化结果， 优化后， 整级涡轮绝热效率增加1.02%， 涡轮输出功率增加1.8%。

关键词： 涵道式冲压涡轮； 气动优化； Kriging模型； 试验设计； 吊舱发电

中图分类号： V231.3 文献标识码： A文章编号： 1673-5048（2016）05-0061-05

Abstract： The ram air turbine is the power component of the pod power supply system （PPSS）， so its performance affects the PPSS efficiency directly. The elevenparametermethod is used to model the twodimensional blade profile of ram turbine， and the threedimensional molding is done to form ram turbine by trailing edge stacking. Using Fluent to analyze the flow field of the turbine， in condition that the mass flow rate and output power are not decreased， taking loss coefficient of turbine as target function， the blades of nozzles and rotors and the aerodynamic configuration of the rotors are optimized based on design of experiments（DOE） and Kriging model. The research results show that the optimization design based on DOE and Kriging model can get good optimization results with less numbers of experiments. The adiabatic efficiency of turbine increases by 1.02% and the output power increases by 1.8% after optimization.

Key words： ducted ram air turbine； aerodynamic optimization； Kriging model； DOE； pod power

0引言

在现代电子对抗中， 电子吊舱的运用非常广泛。 随着电子吊舱耗能的增加， 供电的重要性日益突显， 吊舱自主发电系统是解决这一难题的有效手段。 吊舱自主发电系统分为桨叶式冲压涡轮和涵道式冲压涡轮， 桨叶式冲压涡轮效率低、 发电功率小， 已不能适应如今的电子对抗的需求。 涵道式冲压涡轮以轴流式叶轮机械作为其设计理论， 效率高、 发电功率大， 美国海军已将其纳入“下一代电子对抗机”（NGJ）计划之中[1]，不少研究者针对该计划提出了不同的解决方案[2-4]。

对于涵道式冲压涡轮发电系统， 国内外研究人员针对不同方向进行了不同程度的研究[5-7]。 Ghetzler等[5]提出了一种低阻涵道式冲压涡轮发电系统， 发电功率大、 阻力小， 但由于进气口设置在吊舱前端， 会对雷达信号造成干扰； Robinson等[3]将进气口设在吊舱中段， 并通过控制出口活门开度来控制涡轮出口背压， 进而控制涡轮的转速及运行状态； 王建平等[6]运用数值模拟对涵道式和桨叶式冲压涡轮进行了对比研究， 指出涵道式冲压涡轮效率远高于桨叶式冲压涡轮， 但并没有设计出性能优良的涵道式冲压涡轮； 汪涛等[7]利用数值模拟对飞行包线内涵道式冲压涡轮的性能进行了计算， 探究涡轮效率及功率随飞行表速及飞行高度的变化规律， 指出在高空低飞行速度时涡轮输出功率最低。

国外研究成果相对保密， 国内停留于定性研究， 而未对设计方法提出可行的指导。 本文旨在对此问题进行探究， 利用数值计算结合Kriging近似模型对涵道式冲压涡轮进行气动优化设计。

1Kriging近似模型

1.1Kriging模型简介

Kriging模型最早是由南非矿业工程师D.G.Krige提出并应用于地质统计学中的， 是一种基于统计理论的插值模型。 通过建立输入/输出之间的近似函数关系， 来代替耗时巨大的数值模拟， 现在多用于确定性问题（一个输入只有一个输出）的优化中。

式中： fmin为所有样本点的最小目标函数值； y～为x点处的Kriging模型预测值； s为Kriging模型预测均方根误差RMSE， s=s2。 Φ和分别为标准正态分布函数和正态分布密度函数。 式中的第一项把当前最小目标函数值与预测值的差乘以预测值的提高概率， 当预测值小于当前最小目标函数值时， 第一项会变得较大； 第二项是预测标准差与正态密度函数的积， 当预测精度较低及预测值与当前最小目标函数接近时， 第二项值较大。 所以当某点处的预测值小于当前最小值或该点处的预测精度较低时， EI函数值也会比较大。 EI策略同时考虑了Kriging模型的预测值与预测精度（预测标准差）， 具备很强的自适应性和鲁棒性。 因此， 将EI最大处的样本点作为新的样本点加入样本集中可以有效改善模型的预测精度。

2冲压涡轮气动优化

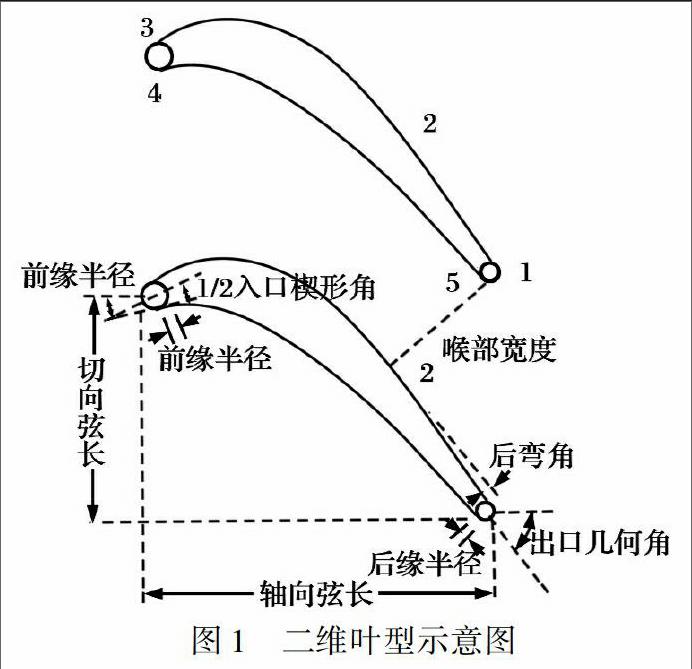
涡轮气动设计经历了一维经验和二维半经验设计体系、 准三维设计体系、 三维设计体系直到现如今的气动优化设计体系。 气动优化设计开始于一维热力计算， 结束于气动优化迭代， 主要涉及叶片造型方法、 优化参数、 气动分析方法及优化策略等的选取， 良好的优化策略组合可以用最少的试验次数达到最佳的优化效果。 各国研究者针对不同的造型方法及优化策略对涡轮叶片的气动优化进行了一系列的研究[10-12]。 本文基于气动优化设计的通用原则， 结合涵道式冲压涡轮自身特点， 选取11参数法[13]进行涡轮叶片叶根、 叶中、 叶尖三截面二维叶型成型， 利用积叠线进行后缘积叠生成三维叶片， 如图1所示。 通过正交试验对优化参数进行选取， 最后利用Kriging模型寻找最优参数使得涡轮绝热效率最大。

2.1试验设计

在进行优化参数选取时， 需要判定各个参数对目标函数的影响水平， 以便用最少的参数达到最佳的优化效果。 正交试验具有“均匀分散， 整齐可比”的特点， 对每个因素和每个水平同等对待， 便于分析处理， 因此本文采用正交试验进行优化参数的选取。

在构建Kriging模型之前， 需要在设计空间内生成一定数量的样本点。 为了有整齐可比性， 对任意两个因素必须是全面试验， 每个因素的各水平必须有重复。 这样不能做到充分“均匀分散”， 且试验的数目必须比较多。 而均匀设计不考虑整齐可比性， 单纯从均匀性出发， 更具代表性。 本文采用均匀设计选取初始样本点。

2.2基于Kriging模型的优化策略

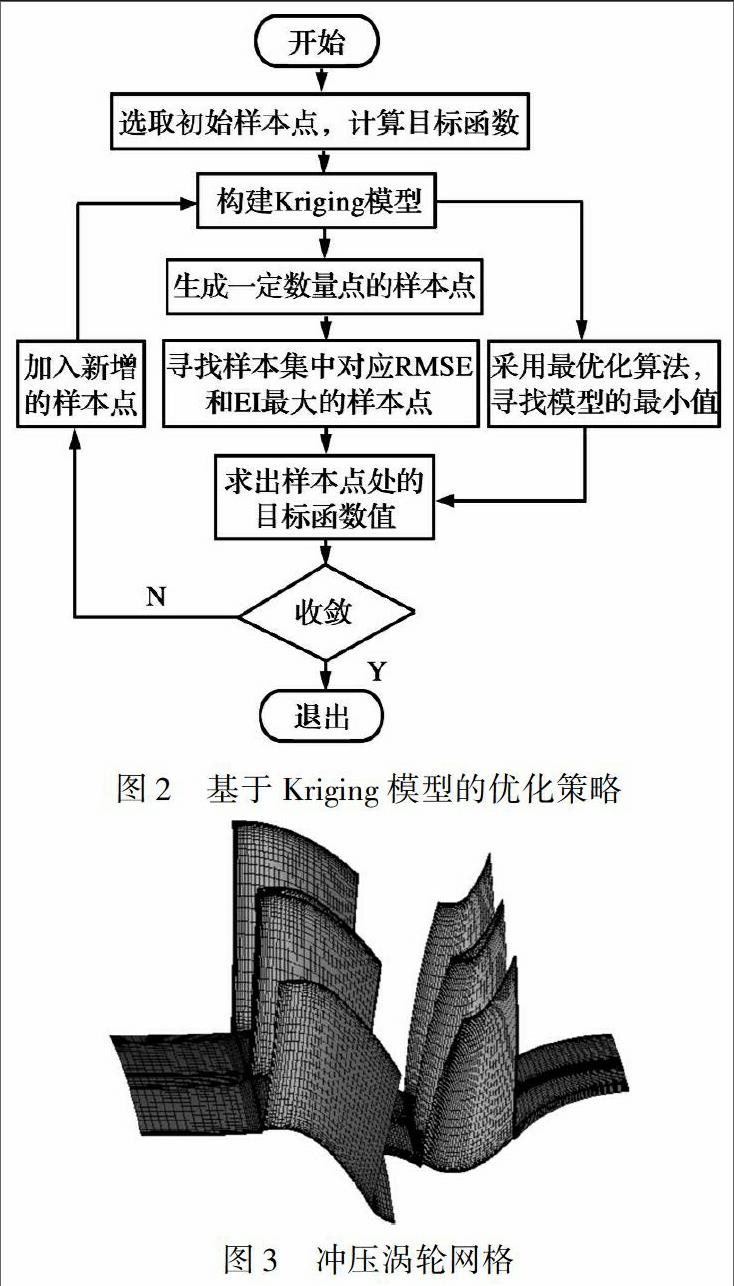
利用Lophaven等[14]开发的DACE-A Matlab Kriging Toolbox求解Kriging模型相关参数， 能够减小模型对初始样本点选择的依赖。 同时将EI方法和最优化算法得到的最优点加入原有样本集， 对Kriging模型进行更新改进， 加快模型收敛速度[15]， 优化流程如图2所示。

2.3涵道式冲压涡轮叶片数优化

为验证优化策略的可行性与有效性， 对设计的冲压涡轮叶片数进行优化， 利用ANSYS ICEM进行网格划分， 采取H型网格， 控制Y+≈1， 经网格无关性验证， 总网格数54万， 网格如图3所示。 利用ANSYS Fluent对冲压涡轮进行流场计算， 湍流模型选取S-A模型， 静子转子交界面处理采用混合面模型， 对静子出口参数作周向平均提供给图3冲压涡轮网格

转子入口。

原始冲压涡轮在设计工况下的试验参数如表1所示， 原始冲压涡轮叶片数及优化区间如表2所示。

3结论

（1） 采取的优化策略能以尽量少的试验次数获得良好的优化效果， 其可行性与有效性通过对冲压涡轮进行气动优化得到了验证；

（2） 设计的冲压涡轮能在设计工况下以92%的效率输出18 kW的能量， 为冲压涡轮的气动设计提供了可借鉴的措施；

（3） 在进行冲压涡轮气动优化设计时， 未考虑涵道引气对涡轮入口气流分布的影响， 在今后的研究中， 要进一步对吊舱-进气道-冲压涡轮系统进行整体分析。

参考文献：

[1] Next Generation Jammer[R].United States Government Accountability Office， 2013.

[2] Gibson M E， Erdmann J T. Inlet and Exhaust System[P]. US， 8714919， 2014-05-06.

[3] Robinson B H， Yook J K， Steele J H. Power Producing Device with Control Mechanism[P].US， 734236， 2013-01-04.

[4] Justak J F， Doux C， Martyr S. Submerged Ram Air Turbine Generating System[P].US，8653688， 2014-02-18.

[5] Ghetzler R， Wojtalik J F，Jr， Kruse N， et al. Low Drag Ducted Ram Air Turbine Generator and Cooling System[P].US， 6270309， 2001-08-07.

[6] 王建平， 朱春玲. 冲压涡轮发电系统数值分析及试验研究[C]∥第二届中国航空学会青年科技论坛， 2006.

[7] 汪涛， 楚武利， 卢家玲， 等. 亚音速涵道式冲压空气涡轮性能数值仿真[J]. 计算机仿真， 2009， 26（10）： 34-38.

[8] 游海龙， 贾新章. 基于遗传算法的Kriging模型构造与优化[J]. 计算机辅助设计与图形学学报， 2007， 19（1）： 64-68.

[9] Jones D R， Schonlau M， Welch W J. Efficient Global Optimization of Expensive BlackBox Functions[J]. Journal of Global Optimization， 1998， 13（4）： 455-492.

[10] Chen Naixing， Zhang Hongwu， Ning Fangfei， et al. An Effective Turbine Blade Parameterization and Aerodynamic Optimization Procedure Using an Improved Response Surface Method[C]∥ASME Turbo Expo 2006： Power for Land， Sea， and Air， 2006： 1169-1180.

[11] Goel S. Turbine Airfoil Optimization Using Quasi3d Analysis Codes[J]. International Journal of Aerospace Engineering， 2009（2009）： 1-14.

[12] Grsel J， Keskin A， Swoboda M， et al. A Full Parametric Model for Turbomachinery Blade Design and Optimisation[C]∥ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference， 2004： 907-914.

[13] Pritchard L J. An Eleven Parameter Axial Turbine Airfoil Geometry Model[C]∥ASME International Gas Turbine Conference and Exhibit， American Society of Mechanical Engineers， 1985.

[14] Lophaven S N， Nielsen H B， Sondergaard J.DACE： A MATLAB Kriging Toolbox[R]. Technical University of Denmark， 2002.

[15] 孟晖. 径—轴流式涡轮优化设计[D]. 南京： 南京航空航天大学， 2014.