磁流变液的流变性能分析

肖林京，王传萍，朱绪力，孙朝阳

(山东科技大学 机械电子工程学院，山东 青岛266590)



磁流变液的流变性能分析

肖林京，王传萍，朱绪力，孙朝阳

(山东科技大学 机械电子工程学院，山东 青岛266590)

制备了以羰基铁粉为磁性颗粒的硅油基磁流变液，使用Anton Paar Physica MCR 301流变仪测试其流变性能，用Bingham模型对磁流变液的流变性能进行拟合计算。实验表明，Bingham模型可较好地描述磁流变液的流变行为。随着磁场的增大，磁流变液的剪切应力和粘度显著增大。磁场不变时，随着剪切速率增加，磁流变液剪切应力增加不明显，符合剪切稀化的Bingham模型。通过对数拟合的方法，得出磁流变液剪切应力和电流的关系，在电流较小时，剪切应力呈指数增长，指数值约为1.42，随着电流的增大，剪切应力达到稳定值。

磁流变液；流变性能；屈服应力；流变模型；磁场

磁流变液是由微米量级的铁磁性颗粒分布于非磁性液体中形成的悬浮液。在外加磁场作用下，磁流变液由原先的粘性流态转化为类固态[1]，其物理性能(如电磁学、力学、热学等性能)同时发生改变[2-4]。磁流变液的这种性能变化称为磁流变效应，具有可控、快速、能耗低、制备方便等特点[5-6]，广泛应用于车辆、建筑结构、医疗器械、运动器材、精密材料抛光和密封等领域[7-9]。

对于磁流变液这类流体，一般采用Bingham模型、Bivisous模型和Herschel-Bulkley模型来描述其流变行为[10]。Bivisous模型在磁流变液的弹性和塑形的过渡阶段存在突变，这在一定程度上不能准确描述磁流变液的流变行为，而三参量的Herschel-Bulkley模型计算复杂，因此多采用精度较高且计算比较简单的Bingham模型来描述磁流变液的流变行为。姚军等[11]研究了羰基铁粉的铁含量对磁流变液剪切屈服强度的影响，发现磁流变液中铁的含量越高，其屈服应力越大。朱绪力等[12]对磁流变弹性体中颗粒磁场力进行了分析，得出了颗粒磁场力与磁场强度之间的关系。易成建[10]对磁流变液的性能进行了测试，并观察了磁流变液的微观变化； Berli等[13]提出一种磁流变液的结构粘度模型；Alghamdi等[14]对磁流变液在传动技术中的应用进行了分析。本实验研究一种磁流变液在磁场作用下的流变行为，分析不同体积比的磁流变液，其剪切屈服应力和磁场强度的依赖关系，为磁流变液的优化及工程应用提供技术依据。

1 磁流变液的流变模型

研究和应用中，一般运用Bingham模型[10,13]表达磁流变液的剪切流动特性。Bingham模型可表示为：

(1)

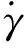
磁流变液的屈服应力是衡量磁流变液性能的一个重要指标[15]。在屈服应力的计算中，引用最多的是美国Ford公司的Ginder等利用Maxwell应力张量得到的计算屈服应力的公式[15-16]。

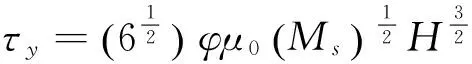
(2)

式中：φ为铁磁性颗粒的体积分数；μ0为磁流变液的磁导率；Ms为铁磁性颗粒的饱和磁化强度；H为磁场强度。

2 磁流变液的制备与实验测试

2.1 磁流变液的制备

制备铁磁性颗粒体积分数分别为10%、20%、30%、40%的磁流变液。按计算的配比称取铁磁性颗粒和基液，铁磁性颗粒采用江苏天一超细金属粉末有限公司的羰基铁粉，其平均粒径为3.3 μm，基液采用二甲基硅油，运动粘度为10-5m2/s，二甲基硅油和表面活性剂来自济南多维桥化工有限责任公司。磁流变液的制备流程如图1所示。羰基铁粉和表面活性剂混合，用搅拌器高速搅拌后，放入真空干燥箱干燥，然后将处理好的铁粉和二甲基硅油混合，放入球磨机进行高速球磨数小时，即可得到磁流变液。制备好的磁流变液样品如图2所示。

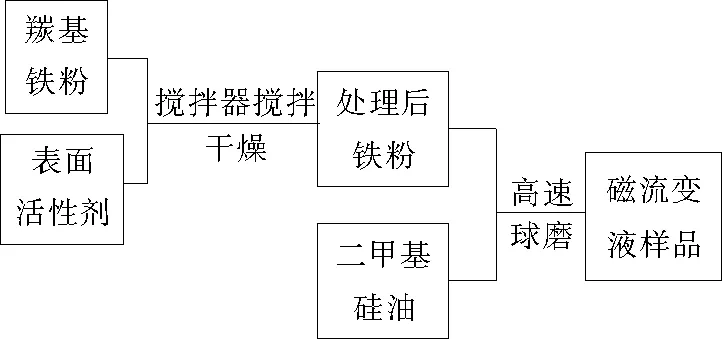
图1 磁流变液的制备流程Fig.1 Preparation process of MRFs

图2 磁流变液样品Fig.2 Sample of MRFs

2.2 磁流变液的微观观测

实验采用Keyence的VHX-600超景深三维数码显微镜对磁流变液在磁场作用下的微观变化进行观察，将制备好的磁流变液滴一滴在载玻片上，盖上盖玻片，使液滴铺展均匀。通过线圈加铁芯装置对磁流变液施加磁场，电流大小设置为1 A。磁流变液的微观变化如图3所示。

图3 磁流变液的微观变化Fig.3 Micro motions of MRFs

由图3可以看出，无磁场作用下，磁流变液中的铁磁性颗粒均匀分散在基液中；磁场作用下，磁流变液中的铁磁性颗粒相互聚集形成链柱结构。

2.3 磁流变液实验测试

使用Anton Paar Physica MCR 301平板测试流变仪测试磁流变液的流变性能。流变仪在工作过程中，通过磁场发生附件(Physica MRD 180)使磁流变液处于一个相对均匀磁场环境中，该附件采用电场控制内置线圈产生均匀的磁场，再经导磁骨架将磁场垂直加到磁流变液上，形成一个闭合的磁路系统。实验测试时，将磁流变液放入测试区，然后在不同条件下测量磁流变液的剪切应力。

将体积分数为30%的磁流变液滴入测试区，电流分别设置为0.5、1、2、4 A，剪切速率设置在0～1 000 s-1范围内变化，测量磁流变液剪切应力的变化，研究磁场作用下，磁流变液剪切应力和剪切速率的关系。然后将四种不同体积分数的磁流变液分别放入测试区，设置剪切速率为300 s-1，电流0～4 A，依次测试不同体积分数的磁流变液剪切应力的变化，研究不同体积分数的磁流变液剪切应力和电流的关系及相同磁场下磁流变液剪切应力和颗粒体积分数的关系。

图4 磁流变液剪切应力和剪切速率的拟合Fig.4 Fitting of shear stress and shear rate of MRFs

3 实验结果与分析

3.1 剪切应力和剪切速率的关系分析

用Bingham模型对磁流变液的剪切应力和剪切速率进行拟合，拟合结果如图4所示。可以看出，磁流变液的剪切应力随剪切速率的变化不明显，存在剪切稀化现象。

磁流变液剪切应力和剪切速率的拟合计算结果如表1所示。可以看出，随着电流的增大，磁流变液的屈服应力和粘度增大。电流从0.5 A增大到4 A时，磁流变液的屈服应力从4.12 kPa增大到32 kPa，粘度从2.26 Pa·s增加到5.89 Pa·s。

表1 磁流变液剪切应力和剪切速率的拟合计算结果Tab.1 Fitting calculation results of shear stress and shear rate of MRFs

在磁场作用下，铁磁性颗粒逐渐形成链状结构，宏观表现为屈服应力。随着剪切速率的增加，链状结构发生倾斜，当倾斜达到一定程度后，颗粒链发生断裂，在磁场作用下，断裂的颗粒链发生重组形成新的颗粒链。由于在剪切过程中，并不是全部的颗粒链在同一时刻断裂，而是部分链发生断裂，部分链依然保持着拉伸倾斜状态，因此随着剪切过程的进行，颗粒链的断裂和重组达到动态平衡，磁流变液的宏观剪切应力趋于稳定。外加磁场越大，颗粒链形成的链柱结构越多，链的平均长度增加，造成磁流变液剪切应力增大。因此相同剪切速率下，磁流变液的宏观剪切应力显著增大。

3.2 剪切应力和外加电流的关系分析

磁流变液剪切应力和电流的关系如图5所示。可以看出，电流增大时，磁流变液剪切应力显著增大，后逐渐达到稳定值，其变化范围为200 Pa～51 kPa。磁流变液中铁磁性颗粒的体积分数越大，剪切应力越大，剪切应力达到稳定值时需要的磁场越大。电流0～2 A，磁流变液剪切应力和电流在双对数坐标下进行线性拟合，拟合结果如图6所示。可以看出，不同体积分数的磁流变液，其剪切应力和电流呈指数关系。

图5 磁流变液剪切应力和电流的关系Fig.5 The relationship between shear stress and current

图6 磁流变液剪切应力和电流的拟合Fig.6 Fitting of shear stress of MRFs and current表2 磁流变液剪切应力和电流的拟合计算结果Tab.2 Fitting calculation results of shear stress of MRFs and current

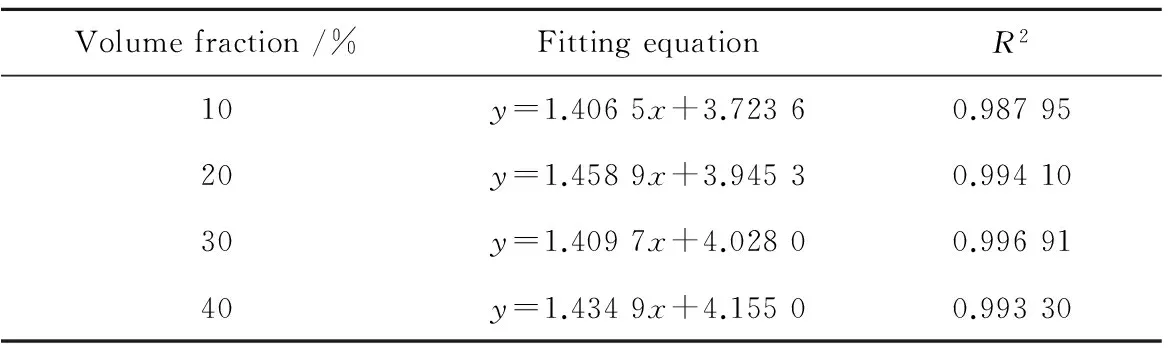
Volumefraction/%FittingequationR210y=1.4065x+3.72360.9879520y=1.4589x+3.94530.9941030y=1.4097x+4.02800.9969140y=1.4349x+4.15500.99330

磁流变液剪切应力和电流的拟合计算结果如表2所示。可以看出，不同体积分数的磁流变液，其剪切应力和电流呈指数关系，指数值约为1.42。磁流变液剪切应力和电流的关系可以用颗粒间磁场力来解释[12]。当磁场较小时，磁流变液内的铁磁性颗粒远未达到磁化饱和，在磁场作用下，颗粒相互作用，形成链柱结构，宏观表现为剪切应力增加显著，呈指数式增长。随着磁场的增大，颗粒接近磁化饱和时，宏观表现为剪切应力达到稳定值。由此可以得出，磁流变液剪切应力和外加电流的依赖关系，在电流较小时，剪切应力表现为指数增长，指数值约为1.42，随着外加电流的增大，剪切应力达到稳定值。

3.3 剪切应力和颗粒体积分数的关系分析

不同体积分数的磁流变液剪切应力变化如图7所示。可以看出，磁流变液内铁磁性颗粒的体积分数从10%增加到40%时，电流为0.5 A时，剪切应力从2.3 kPa增加到6.5 kPa；电流为4 A时，剪切应力从13.5 kPa增加到50 kPa。由此可以得出，随着铁磁性颗粒体积分数的增加，相同电流下对应的剪切应力增大。并且外加电流越大，剪切应力增加越显著。铁磁性颗粒的体积分数越大，铁磁性颗粒间形成的链状结构越密集，宏观表现为剪切应力越大。外加磁场越大，颗粒链形成的链柱结构越多，链的平均长度增加，宏观表现为剪切应力增大。因此相同的颗粒体积分数，磁场越大，磁流变液的宏观剪切应力越大。

图7 磁流变液剪切应力和颗粒体积分数的关系Fig.7 The dependence of shear stress on particle volume fraction

4 结论

通过理论及实验数据分析，可得出以下结论：

1) 用Bingham模型对磁流变液剪切应力和剪切速率进行拟合分析，得出电流从0.5 A增大到4 A时，磁流变液的屈服应力从4.12 kPa增大到32 kPa，粘度从2.26 Pa·s增加到5.89 Pa·s。电流不变时，磁流变液的剪切应力随剪切速率的变化不明显，符合剪切稀化的Bingham模型。

2) 随着电流的增大，磁流变液剪切应力增大，后逐渐达到稳定值，其变化范围为200 Pa～51 kPa。电流在0～2 A范围内时，对磁流变液剪切应力和电流拟合结果分析，得出磁流变液剪切应力与电流呈指数关系，指数值约为1.42，拟合结果与理论分析结果一致。

3) 随着磁流变液内铁磁性颗粒体积分数的增加，相同电流下对应的剪切应力增大，电流越大，剪切应力增加越显著。

[1]GHAFFARI A,HASHEMABADI S H,ASHTIANI M.A review on the simulation and modeling of magnetorheological fluids[J].Journal of Intelligent Material Systems and Structures,2015,26(8):881-904.

[2]贺杰,高丽霞,龙正,等.磁流变液颗粒成链过程的理论和实验研究[J].功能材料,2013,44(4):522-526. HE Jie,GAO Lixia,LONG Zheng,et al.Theoretic and experimental study of chain-formation mechanism for MRF[J].Functional Materials,2013,44(4):522-526.

[3]陈松,李峰,黄金,等.温度对磁流变液材料及传力性能的影响[J].材料导报,2015,29(8):151-155. CHEN Song,LI Feng,HUANG Jin,et al.Influence of temperature on magnetorheological fluid and transmission performance[J].Materials Review,2015,29(8):151-155.

[4]张平,刘奇,唐龙,等.高性能磁流变液的稳定性及应用[J].功能材料,2010,41(6):965-968. ZHANG Ping,LIU Qi,TANG long,et al.Stabilities and applications of magnetorheological fluids[J].Functional Materials,2010,41(6):965-968.

[5]杨健健,晏华,王雪梅,等.不同粒径SiO2粒子对磁流变液性能的影响[J].功能材料,2014,45(4):4095-4099. YANG Jianjian,YAN Hua,WANG Xuemei,et al.The effect of SiO2particle size on the performance of magnetorheological fluids[J].Functional Material,2014,45(4):4095-4099.

[6]ASHTIANI M,HASHEMABADI S H,GHAFFARI A.A review on the magnetorheological fluid preparation and stabilization[J].Journal of Magnetism and Magnetic Materials,2015,374:716-730.

[7]唐龙,岳恩,罗顺安,等.磁流变液温度特性研究[J].功能材料,2011,42(6):1065-1067. TANG long,YUE En,LUO Shun'an,et al.Study on temperature performance of magnetorheological fluids[J].Functional Materials,2011,42(6):1065-1067.

[8]IMADUDDIN F,MAZLAN S,ZAMZURI H.A design and modelling review of rotary magnetorheological damper[J].Materials and Design,2013,51(5):575-591.

[9]陈飞,田祖织,王建.温度对磁流变液流变性能的影响研究[J].功能材料,2014,45(20):20095-20098. CHEN Fei,TIAN Zuzhi,WANG Jian.Influence of temperature on the performance of magnetorheological fluid[J].Functional Materials,2014,45(20):20095-20098.

[11]姚军,张进秋,彭志召,等.羰基铁粉的铁含量和粒径对磁流变液剪切屈服强度的影响[J].材料研究学报,2014,28(12):955-960. YAO Jun,ZHANG Jinqiu,PENG Zhizhao,et al.Influence of Fe content and particle size of carbonyl iron powder on shear yield stress of magnetorheological fluids[J].Journal of Materials Research,2014,28(12):955-960.

[12]朱绪力，孟永钢，田煜.磁流变弹性体中颗粒磁场力的简化分析模型[J].功能材料，2010,41(10):1712-1715. ZHU Xuli,MENG Yonggang,TIAN Yu.A simplified analytical model of magnetic force between particles in magnetorheological elastomers[J].Functional Materials,2010,41(10) :1712-1715.

[13]BERLI C L A,DE VICENTE J.A structural viscosity model for magnetorheology[J].Applied Physics Letters,2012,101(2):021903.

[14]ALGHAMDI A A,LOSTADO L R,OLABI G A.Magneto-rheological fluid technology[M]// Modern Mechanical Engineering.Berlin，Heidelberg： Springer，2014,252(1/2/3):43-62.

[15]MUHAMMAD A,YAO X L,DENG Z C.Review of magnetorheological (MR) fluids and its applications in vibration control[J].Journal of Marine Science and Application,2006,5(3):17-29.

[16]BOSSIS G,KHUZIR P,LACIS S,et al.Yield behavior of magnetorheological suspensions[J].Journal of Magnetism and Magnetic Materials,2003,258-259:456-458.

(责任编辑：吕海亮)

Rheological Performance Analysis of Magnetorheological Fluids

XIAO Linjing,WANG Chuanping,ZHU Xuli,SUN Zhaoyang

(College of Mechanical and Electronic Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)

Silicone-based magnetorheological fluids (MRFs) were prepared with carbonyl iron powder as magnetic particles and its rheological performances were tested with Rheometer Anton Paar Physica MCR 301 and calculated with Bingham model.The experimental results show that Bingham model can well describe the rheological behaviors of MRFs.The shear stress and viscosity of MRFs increase significantly with the increase of magnetic field.However,when the magnetic field keeps the same,there is no apparent increase in shear stress with the increase of shear rate,which conforms to the Bingham model of shear thinning.The relationship between shear stress and electric current of MRFs was obtained by using logarithm fitting.It is found that the shear stress of MRFs firstly increases exponentially with the index value being about 1.42 when the current is small,but it tends to be stable as the current increases.

magnetorheological fluid; rheological performance; yield stress; rheological model; magnetic field

2016-01-08

山东省自然科学基金项目(ZR2011EEM005)

肖林京(1966-)，男，山东临沂人，教授，博士，研究方向为机电传动控制.E-mail:1527510435@qq.com 王传萍(1991-)，女，山东临沂人，硕士研究生，研究方向为磁流变材料减振.E-mail:wangchuanping10@163.com

TM271;TF125.8

A

1672-3767(2016)06-0043-06