三阶常微分方程的线性化
周元任,王 麒,许文祥,朱晓宇,雷 丽
(中国矿业大学(北京) 理学院,北京 100083)
三阶常微分方程的线性化
周元任,王 麒,许文祥,朱晓宇,雷 丽
(中国矿业大学(北京) 理学院,北京 100083)
研究三阶常微分方程的线性化,可便于对三阶常微分方程进行求解.通过可逆的变量变换,将所有可线性化的三阶常微分方程转化成三阶程常微分方程的规范形式,进而得到它的通解.由于变量变换是可逆的,所以两种形式可以互相转化,从而可以利用该方法将一般三阶常微分方程转化成三阶常微分方程的规范形式.
变量变换;可线性化;三阶常微分方程
1 三阶常微分方程的规范化
由于一般三阶常微分方程(ODE)比较繁琐,难以求解,所以需要找到将一般三阶常微分方程转化成线性化的三阶常微分方程(三阶常微分方程的规范形式)的方法.
1.1.背景
一般线性齐次方程

可以写成如下二项式系数的标准形式:

E.拉盖尔于1879年证明了方程(1.2)里最高阶数以下的两个阶次项可以同时被消去,相应的结果可以用如下定理来表述:
定理1.1 n阶常微分方程(1.2)可以通过合适的等价变换

1.2 主要思想
三阶方程的规范形式为

方程(1.4)很显然是线性的,那接下来的问题是,哪些三阶ODE可以线性化为(1.4)呢?下面我们给出可线性化的三阶方程的形式.
定理1.2 形如

的三阶方程可以通过等价变换
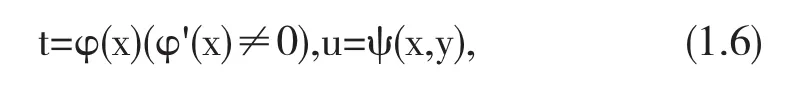


2 相关例题
例 将下列方程线性化



〔1〕Ibragimov N.H.,CRC handbook of Lie group analysisofdifferentialequations,CRC Press Inc.,Boca Raton,1994.
〔2〕Olver P.J.,Applications of Lie groups to differential equations,Springer,New York,1986.
〔3〕Ibragimov N.H.and Meleshko S.V.,J.Math.Anal.Appl.,308(1),2005,266-289.
〔4〕卢琦等.微分方程与数学物理问题.北京:高等教育出版社,2010.
O175.1
A
1673-260X(2016)11-0001-02
2016-07-17

