基于遗传算法的水下机器人滑模变结构控制策略

徐 强，章家岩，杜翠翠，冯旭刚

(安徽工业大学电气与信息工程学院，安徽马鞍山243032)

基于遗传算法的水下机器人滑模变结构控制策略

徐 强，章家岩，杜翠翠，冯旭刚

(安徽工业大学电气与信息工程学院，安徽马鞍山243032)

针对水下机器人需快速、准确跟踪目标的要求，在分析其非线性四自由度动力学模型的基础上，运用李雅普诺夫稳定性分析法，提出一种基于遗传算法的水下机器人滑模变结构控制方法。设计遗传-滑模控制器，利用遗传算法对控制器参数进行优化以消减抖振，并通过动态选优，选取全局最优解，进而提高收敛速度，实现运动状态的实时调整。仿真结果表明，该控制方法能够高效地获取全局最优解，并具有较强的自适应能力，能够有效地实现水下机器人的轨迹跟踪。

水下机器人；遗传算法；滑模控制；轨迹跟踪

水下机器人(AUV)是一种能够进行轨迹跟踪并完成水下观测作业的自动化装置，被广泛应用于海洋勘探、海洋石油开发、海上抢险打捞等领域[1-2]。实现AUV控制系统的高精度轨迹跟踪是确保其在水下进行复杂作业并稳定可靠工作的关键，也是目前水下机器人的一个重要研究方向。

AUV具有很强的非线性、耦合性、时变性和参数的不确定性，难以获得精确的水动力系数，而来自水流和波浪等外部扰动使路径规划建模变得较为困难[3-5]。目前，多采用模糊控制[6]、非线性控制[7]、自适应控制[8-9]和神经网络控制[10]进行AUV的运动控制。如，文献[11]通过构建生物启发模型，结合滑模控制方法，解决AUV跟踪控制的速度跳变问题，但只讨论了二维平面情况，对于三维立体轨迹跟踪问题则没有考虑；文献[12]针对关节型机器人点对点路径规划问题，提出基于约束条件的遗传算法控制策略，但没有考虑多自由度机器人轨迹规划问题；文献[13]将具有量子行为的粒子群算法运用到机器人路径规划之中，并分析机器人运动轨迹的收敛性，提出一种改进的轨迹规划方法且应用于机器人实验平台，但该方法没有考虑实际现场干扰的影响。而构建遗传-滑模控制器并应用于AUV控制的研究报道并不多见，为此，本文将遗传算法与滑模控制相结合，实时优化参数，通过运动轨迹控制，实现对AUV的高精确位置跟踪。

1 水下机器人动力学分析

文中考虑一个非线性四自由度模型，设定阻尼力无耦合、重心和浮心重合及水动力系数为常数。采用4个推进器驱动AUV，如图1。其中AUV手臂上外露螺旋桨(Tx1，Tx2)用于水平运动，升沉运动则依靠垂直螺旋桨(Tz1，Tz2)。

AUV动力学方程[14]可表示为

为使AUV保持平稳运行，通常假设AUV为低速移动，此时，惯性矩阵和矩阵可表示为[15]：

其中：X，Y，Z分别为AUV在x，y，z方向的惯量；N为AUV姿势惯量。阻尼力在低速运动中可认为无耦合，则水动力阻尼力可表示为

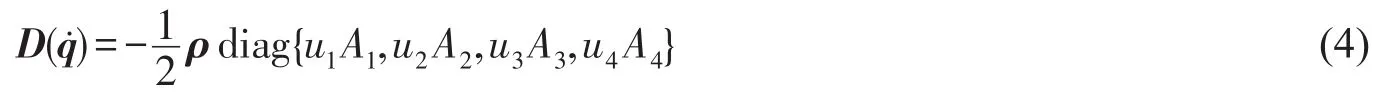
其中：u1，u2，u3，u4为AUV在x，y，z及姿势方向的阻力系数；A1，A2，A3，A4为AUV在x，y，z及姿势方向的断面面积。引力矢量G可表示为

其中：m为AUV的质量；V为流体流过AUV的体积；g为重力加速度；ρ为流体密度。

图1 AUV结构示意图Fig.1 Diagram ofAUV structure

2 控制算法设计

2.1 滑模变结构控制

滑模变结构控制策略的特点在于控制的不连续性，致使系统在一定规则下沿规定的状态轨迹做小幅度、高频率运动，约束系统的状态变量，进而使系统始终位于预定曲线(或曲面)的邻域内运动，这就是所谓的“滑动模态”或“滑模”运动。滑模变结构控制是通过高增益的继电器切换将系统的状态约束在滑模面上。理想情况下，系统状态测量精确无误，控制量不受约束，滑动模态光滑运动且渐近稳定于原点，不会产生抖振。为实现这一过程，设计一个滑模变结构控制器跟踪设定轨迹，使控制器的产生状态x(t)跟踪所需的参考轨迹xd(t)。没跟踪误差矢量为

其中：e(t)为跟踪误差；xd(t)为参考轨迹。滑动面[16]定义为

其中J为常数序数。当t≥0，则滑动面的动态系统可表示为

系统动态参数如上升时间、超调量、沉降时间及λ值可动态选择。由式(6)可知，在系统参数有扰动时，单纯滑模控制不能保证系统的控制性能，为此，文中设计遗传-滑模控制器来优化系统参数。

2.2 遗传-滑模控制器构建

遗传算法(简称GA)将生物进化理论引入优化参数中，选择适当适配值函数并通过遗传中的复制、交叉和变异筛选个体，组成新群体，周而复始，达到全局最优解。在创建新一代个体后，计算群体每个成员的适配值函数，若进化方向正确，则获得合适的控制作用。该算法在处理非线性问题时具有较好的鲁棒性，采用GA对滑模控制器参数和切换面函数进行优化，可较好地消除“抖振”。滑模面应保持S=0的状态，为满足这一条件，适配值函数可定义为指数函数F(S)，

其中ξ为常量。从当代群体创造新一代，z需选择精英染色体参与生产下一代。对于四自由度AUV，应进行四类精英选择。最初，随机选择个体，每一自由度的控制行为来自操作区域的随机选择(上标i表示自由度的序数)。通过比较所有个体的适用价值，判定价值最大的个体为精英，若新个体控制行为的适用价值高于前次个体，则该个体将判定为新的精英。

采用交叉操作重塑遗传-滑模控制器，用以产生拥有先代特征的后代，滑动面交叉操作的形式如下

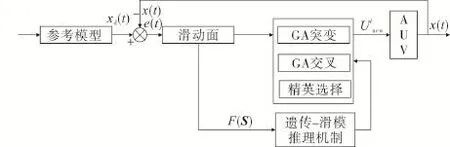
图2 遗传-滑模控制系统框图Fig.2 System chart of GA-sliding mode control

交叉处理后，若控制动作不能使系统保持在滑动面上，采用突变操作迫使系统靠近滑动面。若适配值低于指定值FB，则突变发生；若适配值高于指定值FB，则突变不发生。

遗传-滑模控制器的主要实现步骤如下：

1)选择群体规模K和适配值函数F(S)；

2)生成初始群体；

5)比较适配值和指定值FB，若不低于指定值则进行步骤7)，否则进行步骤6)；

6)突变操作；

7)输出控制行为；

8)判断动作是否完成，若是则结束，若不是则进行步骤3)。

3 仿真结果与分析

对于AUV控制，需考虑四自由度AUV的运动方程，4个电机驱动推进器控制4个可控自由度。考虑机体协调性，系统参数可设置为：AUV的起始坐标为(1 000，5 000，10 000)，单位mm。适配值FB=0.02，惯性矩阵，阻尼矩阵，引力矢量G设置如下：

滑动面常量ξ =10，常数矢量 λ设置为

AUV低速v1=50，20，10 mm/s，高速v2=300，200，100 mm/s。基于遗传-滑模控制的AUV低速、高速轨迹跟踪仿真曲线分别如图4，5（右侧为局部放大图）。

由图4可以看出，AUV在低速运动状态下，跟踪轨迹与设定轨迹基本重合，其运动轨迹波动较小，动态误差小，可实现AUV有效跟踪设定轨迹。

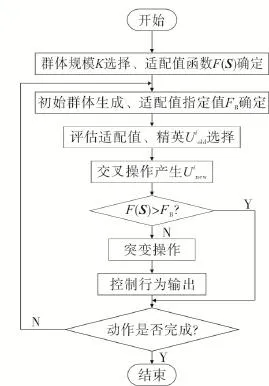
图3 遗传-滑模控制算法流程图Fig.3 Flow chart of GA-sliding mode control algorithm

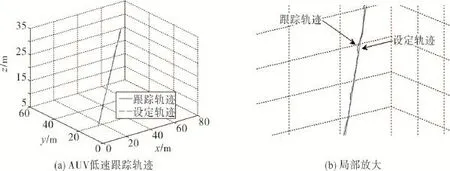
图4 AUV低速轨迹跟踪效果Fig.4 Effective ofAUV low speed trajectory tracking

图5 AUV高速轨迹跟踪效果Fig.5 Effective ofAUV high speed trajectory tracking

由图5可知，AUV在较高速度状态下运动时，其运动轨迹与设定轨迹重合度较高，在部分时段有一定的分离，但AUV能够及时调整运动轨迹，使运动轨迹动态误差保持在较小的范围。综上分析可知，针对AUV轨迹控制，遗传-滑模控制策略具有较好的控制品质、较稳定的控制效果和较强的自适应能力，能够较好地满足AUV高精度轨迹跟踪的控制要求。

4 结 论

以四自由度水下机器人为研究对象，针对其参数的不确定性及其运动环境的复杂性，运用滑模变结构控制原理，通过遗传算法交叉和突变操作，设计遗传-滑模复合控制方法，并将其应用于水下机器人运动轨迹跟踪，以实现对AUV的高精度位置控制。仿真结果表明：遗传-滑模复合控制方法能够高效地选取全局最优解并具有快速收敛能力；基于遗传算法的复合滑模水下机器人控制系统能够精确跟踪参考轨迹，并能在一个较宽的操作范围及不确定情况下实现有效跟踪控制，具有一定的工程应用价值。

[1]张铭钧，褚振忠.自主水下机器人自适应区域跟踪控制[J].机械工程学报，2014,35(4)∶779-784.

[2]GOODMAN L，LEVINE E，WANG Z K.Subsurface observations of surface waves from an autonomous underwater vehicle[J].IEEE Journal of Oceanic Engineering,2010,32(7)∶952-9830.

[3]范士波，连琏，任平.开基于水动力实验的深海开架式潜水器三维轨迹跟踪控制平台设计[J].船舶力学，2011,15(9)∶981-987.

[4]ZANDI R，KAMAREI M，AMIR H.Underwater sensor network positioning using an AUV moving on a random waypoint path[J].IETE Journal of Research,2014,61(6)∶693-698.

[5]BYME S，SCHMIDT V，HEGRENAES O.AUV-acquired bathymetry methods scrutinizing AUV mission planning operations and date processing[J].Sea Technolgy,2015,56(11)∶17-26.

[6]赵文德，李见朋，张铭钧，等.基于浮力调节的AUV深沉运动控制技术[J].南京航空航天大学学报，2010,42(4)∶411-417.

[7]苏玉民，曹建，徐峰，等.鱼雷形水下机器人非线性航迹跟踪控制[J].上海交通大学学报，2012,46(6)∶977-983.

[8]黄海，张强，张树迪，等.欠驱动AUV自适应编队控制策略[J].哈尔滨工程大学学报，2015,36(5)∶633-643.

[9]GALCERAN E，CAMPOS R，PALOMERAS N，et al.Coverage path planning with real-time replanning and surface reconstruction for inspection of three-dimensional underwater structures using autonomous underwater vehicles[J].Journal of Field Robotics, 2015,32(7)∶952-9830.

[10]姜述强，金鸿章，魏凤梅.可容错的遥控水下机器人递归神经网络控制[J].哈尔滨工业大学学报，2013,45(9)∶57-63.

[11]孙兵，朱大奇，邓志刚.开架水下机器人生物启发离散轨迹跟踪控制[J].控制理论与决应用，2013,30(4)∶454-462.

[12]甘亚辉，戴先中.基于遗传算法的多机器人系统最优轨迹规划[J].控制理论与应用，2010,27(9)∶1245-1252.

[13]李仁府，独孤明哲，胡麟，等.基于QPSO算法移动机器人轨迹规划与实验[J].控制与决策，2014,29(12)∶2151-2157.

[14]贾鹤鸣，张利军，齐雪.基于神经网络的水下机器人三维航迹跟踪控制[J].控制理论与应用，2012,29(7)∶877-883.

[15]JAVADI M,BAGHERIA.An adaptive neuro-fuzzy sliding mode based genetic algorithm control system for under water remotely operated vehicle[J].Expert Systems withApplications,2010,32(8)∶647-660.

[16]秦斌，周浩，杜康.基于RBF网络的风电机组变桨距滑模控制[J].电工技术学报，2013,28(5)∶37-41.

责任编辑：何莉

Sliding Mode Variable Structure Control Strategy of Underwater Vehicle Based on GeneticAlgorithm

XU Qiang,ZHANG Jiayan,DU Cuicui,FENG Xugang
(School of Electrical Engineering and Information,Anhui University of Technology,Ma'anshan 243032,China)

To track the target quickly and accurately,based on the analysis of the four degree of freedom nonlinear dynamic model,and with Lyapunov stability analysis method,a sliding mode variable structure control method for autonomic underwater vehicle(AUV)was proposed.A genetic-sliding mode controller was designed,and its parameters were optimized with genetic algorithm to reduce vibration.In addition,the global optimal solution was chosen dynamically,so as to improve the convergence speed,and implement the motion state real-time adjustment.The simulation results demonstrat that the method can obtain the global optimal solution efficiently with better self-adaptive ability and can realize the trajectory tracking of theAUV efficiently.

underwater vehicle;genetic algorithm;sliding mode control;trajectory tracking

TP 273

A

10.3969/j.issn.1671-7872.2016.03.012

2016-01-24

安徽省教育厅自然科学重点项目(KJ2015A058)

徐强(1991-)，男，安徽芜湖人，硕士生，主要研究方向为复杂工业系统建模与优化控制。

章家岩(1963-)，男，安徽铜陵人，教授，主要研究方向为复杂工业系统建模与智能控制。

1671-7872(2016)03-0261-05