基于压缩域的直扩测控信号干扰抑制算法

秦国领，吴小东，张海奇，牛攀峰

(酒泉卫星发射中心，甘肃酒泉732750)

基于压缩域的直扩测控信号干扰抑制算法

秦国领，吴小东，张海奇，牛攀峰

(酒泉卫星发射中心，甘肃酒泉732750)

压缩感知理论突破了经典采样理论的束缚，可有效缓解直扩测控信号大带宽采样引起的信号处理和数据存储的压力。通过分析直扩测控信号与干扰信号的差异，提出一种压缩域直扩测控信号自适应干扰抑制算法。该算法基于直扩测控信号特点构建相应的稀疏基，分析直扩测控信号与干扰信号在稀疏基下的归一化残差及其变化规律，通过稀疏系数重构直扩测控信号，并结合归一化残差变化率实现算法的自适应控制。仿真结果表明，所提算法能够有效抑制干扰信号，采用该算法的检测概率和误码率较直接处理分别提高了3 dB和2 dB。

压缩感知；直扩测控信号；干扰抑制；压缩域

直扩测控系统是基于直扩体制发展的新一代测控系统，具有隐蔽性好、抗干扰能力强的特点[1]。直扩测控信号的伪码速率较高，目前规划建设的宽带直扩测控系统的伪码速率甚至达到百兆量级，这无疑对接收前端的信号采样和后续的同步解调、传输处理造成负担。压缩感知[2]，又称“压缩传感”。Candes指出[3]，如果信号是稀疏的或可压缩的，则可用一个与稀疏基不相关的观测矩阵将高维信号映射到一个低维空间上，并可通过求解稀疏最优化问题将原始信号高概率地精确重建。压缩感知理论突破了经典采样理论的束缚，有效缓解直扩测控信号大带宽采样引起的信号处理和数据存储的压力。

已有研究者对基于压缩感知的直扩测控信号处理进行了研究，如文献[4]从稀疏字典构造入手，对直扩测控信号的稀疏性进行了探讨；文献[5]针对GNSS接收机数据采集存在硬件要求高、计算复杂的问题，基于压缩感知理论，提出了一种直扩信号采集方法；文献[6]为解决信号压缩域载波同步问题，提出了改进的Costas载波跟踪环，不需进行信号重构处理便可提取频率和相位信息；文献[7]对传统伪码跟踪环进行改进，提出一种随机解调压缩采样的压缩域跟踪环，实现了伪码延时相位信息的直接获取；文献[8]基于最小输出能量准则，并运用空间投影技术，实现干扰信号的检测和抑制；文献[9]从构造直扩测控信号和多音干扰的稀疏基出发，利用2种信号稀疏基的差异对干扰信号对应的稀疏向量系数置零实现干扰抑制。总之，有关压缩域直扩测控信号处理的研究涉及多个层面，但是就压缩域抗干扰而言，多是从稀疏系数取值进行选择重构，干扰抑制效率不高。本文基于直扩测控信号和干扰信号稀疏基的差异特点，提出一种压缩域直扩测控信号自适应干扰抑制算法，以期能够抑制各类常规干扰。

1 基于压缩感知的直扩测控信号理论

1.1 直扩测控原理

直扩测控系统是通过将待传输信号与高速率的伪码信号相乘来控制载波信号的某个参量，实现传输信号带宽的扩展[10]。系统的简化框图如图1所示。

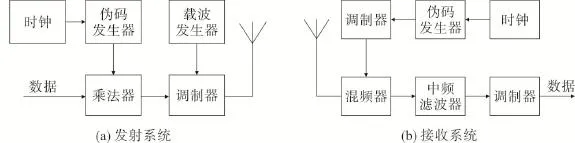
图1 直扩系统简化框图Fig.1 Simplified block diagram of direct spread spectrum system

由图1可知：在发送端，待传输的数据信号与伪码序列相乘，形成复合码对载波进行调制，并通过天线将信号发出；在接收端，产生一个与发送端伪码同步的本地参考伪码序列，对接收信号进行捕获解调处理，最终获得传送的信息。

1.2 压缩感知原理

对于采样长度为N的信号x，Ψ=[φ1,φ2,…,φm,…,φN]为N×N维的稀疏基[11]。如果将x投影到基Ψ上可得到系数向量，即

利用一个M×N维的测量矩阵Φ=[ψ1,ψ2,…,ψi,…,ψN]对信号x进行压缩测量，得到相应的降维观测值y=[y1,y2,…,yi,…,yM]：

其中M/N为压缩比。如果测量矩阵Φ与稀疏基Ψ非相干，则可利用1-范数实现S的精确重构

代入(1)式即可完成信号x的重构。稀疏表示、压缩测量和信号重构是压缩感知理论主要涉及的内容，其基本原理如图2所示。

1.3 直扩测控信号的稀疏表示

由于伪码序列的随机特性，扩频后的信号无论在时域还是频域均不具备稀疏特征。文献[12]指出直扩序列可利用其伪码值分布在信号域进行稀疏分解。假设数据信息为bk∈{±1}N×1，伪码为Pk∈{±1}L×1，则直扩测控信号dk(t)可表示为：

其中：Tb和Tp分别为数据信息和伪码序列的码元长度；N为数据信息长度；L为伪码周期；rect(t)为门函数。

根据计算可知，对于周期为M的伪码序列，其直扩数据信息的可能形式共有2M种。因此dk(t)可表示为

其中Sk为只含一个非零元素的列向量。考虑到Φ(t)的列与列非相干，因此可将Φ(t)作为直扩测控信号的稀疏字典。

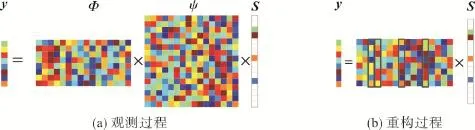
图2 压缩感知原理框图Fig.2 Block diagram of compressed sensing principle

2 基于压缩感知的直扩测控信号干扰抑制算法

2.1 问题模型

设接收信号x由直扩测控信号xS、干扰信号xj和高斯噪声xg组成，即

则存在稀疏基Ψ使xS满足

其中S为直扩测控信号xS对应的系数向量。基于压缩感知理论，时域信号x的观测值y为

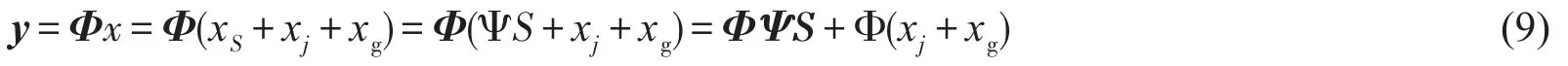
由式(9)可知，如果干扰信号在稀疏基Ψ上不具备稀疏性，则可基于重构算法利用信号y重构直扩测控信号xS，实现干扰信号的抑制。

2.2 干扰和噪声信号的稀疏性验证

干扰信号主要包括宽带干扰、音调干扰、二进制相移键控（Binary Phase Shift Keying，BPSK）干扰、扫频干扰等[13]。干扰信号与稀疏基Ψ的相关特性未知，为实现干扰信号的抑制，需通过定量计算得到相应的相关值。

归一化残差定义为信号重构时每次迭代后的剩余能量与总能量的比值，反映迭代前后信号的能量变化，且直扩测控信号的归一化残差值变化明显[9]，计算式如下

表1 不同信号的基本参数Tab.1 Basic parameters of different signal

表2 不同信号在稀疏基Ψ下的归一化残差及变化率Tab.2 Normalized residual and its change rate of different signals under the sparse matrixΨ

由表2可知，直扩测控信号与干扰信号在稀疏基Ψ下的归一化残差差异明显：稀疏基Ψ是基于直扩测控信号构造的，因此直扩测控信号的归一化残差值为0(计算中不存在干扰和噪声)；干扰信号的归一化残差随着迭代次数的增加而减小，但经过4次迭代后的归一化残差仍然大于0.8；干扰信号归一化残差变化率随着迭代次数的增加而变小，而直扩测控信号归一化残差值的变化率为0。

2.3 算法分析

由2.2节可知，直扩测控信号构造的稀疏基Ψ不能重构出干扰信号，因此可基于稀疏基Ψ重构直扩测控信号xS，实现干扰信号的抑制。由于算法是通过迭代运算实现信号重构，因此迭代次数是影响信号重构的重要因素。为实现计算数量和精确程度的折衷，需设计一个阈值实现迭代次数的自适应停止。

设观测信号y可分解为

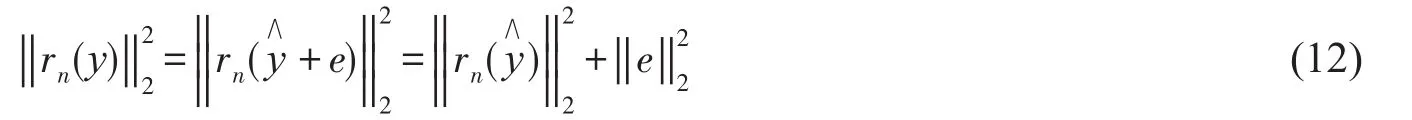
由式(12)可知

然而，随着迭代次数的增加，虽然重构信号的精准度不断提高，但是运算量也随之增加，考虑到残留信号中干扰和噪声信号的能量未知，因此以能量作为迭代停止条件会导致阈值门限不容易设定。

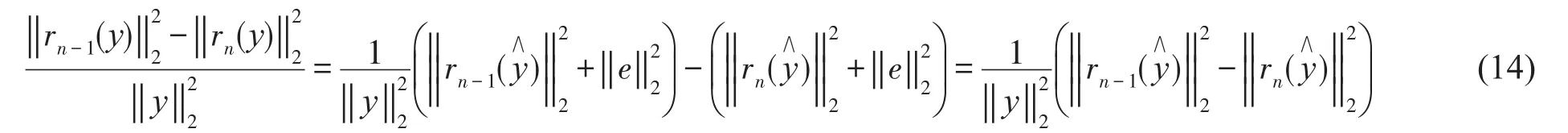
从式(14)中发现相邻两次迭代残差信号的能量差可以消除噪声的影响，将会在有限次迭代后趋近于零，因此可将式(14)所示的归一化残差变化率作为干扰抑制算法迭代停止的条件，即

其中σ为阈值门限。

2.4 算法设计

算法为基于直扩测控信号的稀疏基重构直扩测控信号，并利用归一化残差变化率，实现直扩测控信号的自适应重构，完成干扰信号的抑制，获得信号的接收解调。对该算法的描述如下：

1)初始化初始残差r=y，变量矩阵A=[]赋空；

2)确定内积最大值残差r与Θ的所有列向量Θi，分别求内积，确定内积最大值，即u=argmaxxj=1,2,…，N|＜r,Θj＞|;

3)更新变量矩阵对应更新变量矩阵A=[A,Θu]，并对u的对应列Θu赋空；

4)计算稀疏系数利用最小二乘方法计算稀疏系数λ=(ATA)-1ATy；

5)更新残差计算新的残差，r=y-Aλ；

6)归一化残差计算归一化残差η=‖r‖2/‖y‖2；

7)迭代次数判决是否进行2次迭代？是，则进入步骤2)，否，则进入步骤8)；

8)自适应迭代停止计算最新的归一化残差变化率，如果归一化残差变化率小于阈值门限，即η＜σ，则进入步骤9），否则进入步骤2）；

9)信号重构计算得到重构信号r=y-r；

10)信号解调对信号进行捕获跟踪，解调原始数据信息。

因此可确定算法的检测流程，如图3所示。

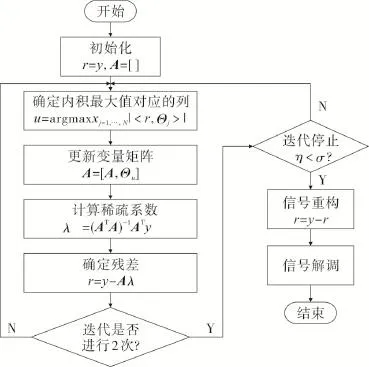
图3 算法的信号检测流程图Fig.3 Signal detection flow diagram of algorithm

3 仿真结果与分析

信号的捕获和解调是直扩信号处理的关键环节，为进一步探析算法的特点，选择体现信号捕获和信号解调的重要指标进行仿真分析，验证算法的有效性。仿真参数如表1，概率结果为相同条件下10 000次实验的统计平均，观测点数为N/5，信噪比(Signal Noise Rate，SNR)为20 dB。

3.1 干扰信号对检测性能的影响分析

参数：干信比(Jamming Signal Rate，JSR)遍历范围-10～20 dB，步进间距2 dB。检测概率是表征直扩测控信号捕获性能的重要指标，定义为伪码相位相关峰值大于判决门限值的概率[14]。基于蒙特卡罗[15]对本文提出的自适应抗干扰算法进行仿真，得到不同干信比下使用和未用自适应抗干扰算法的检测概率，结果如图4。

由图4可知：直扩测控信号的检测概率随着干信比的提高而不断降低，且当干信比超过抗干扰门限后，检测性能急剧下降；不同干扰信号对检测性能的作用影响不同，音调干扰和BPSK干扰的作用效果最为明显；自适应干扰抑制算法对不同干扰的抑制效果不同，对宽带和扫频干扰的抑制效果最为明显，这与宽带和扫频干扰的归一化残差较大相一致；与未使用抗干扰抑制算法相比，采用自适应干扰抑制算法检测性能提高了约3 dB。

3.2 干扰信号对解调性能的影响分析

参数：干信比遍历范围为-10～20 dB，步进间距为2 dB。误码率是反映直扩测控信号解调性能的重要指标，基于蒙特卡洛仿真得到不同干信比下使用和未用自适应抗干扰算法的误码率，结果如图5所示。

由图5可知：直扩测控信号的误码率随着干信比的提高而不断增加，且当干信比超过26 dB后，采用自适应干扰抑制算法的作用效果不明显，这是由于干信比的持续增加导致信号解调性能急剧下滑所致；不同干扰信号对误码率的影响程度不同，音调干扰的作用效果最为明显；自适应干扰抑制算法对不同干扰的抑制效果相似，通过应用自适应干扰抑制算法其解调性能至少提高了约2 dB。

图4 不同干信比下的检测概率Fig.4 Detection probability at different jamming signal rates

图5 不同干信比下的误码率Fig.5 Bit error rate at different jamming signal rate

4 结 论

针对直扩测控信号与干扰信号稀疏性的差异，结合归一化残差的变化规律，提出一种自适应干扰抑制算法。该算法通过迭代比较稀疏系数的差异，实现压缩域多种干扰信号的自适应处理，且通过蒙特卡洛仿真得到不同干信比下检测概率与误码率的性能变化。仿真结果表明：采用自适应干扰抑制算法，直扩测控信号的检测概率和误码率性能至少分别提高了3 dB和2 dB，捕获性能和解调性能得到一定改善。算法计算简单，有效降低系统采样速率，应用前景广阔。对于其他的压缩感知信号，只要选择针对性的稀疏基，本文算法仍具有适用性，这也是笔者下一步的研究方向。

[1]刘嘉兴，文吉.Ka频段混沌扩频测控系统的设想[J].电讯技术，2009,49(5)∶33-37.

[2]DONOHO D.Compressed sensing[J].IEEE Trans on Information Theory,2006,52(4)∶1289-1306.

[3]CANDES E.Compressive sampling[C]//Proceedings of the International Congress of Mathematicians Madrid.Spain∶European Mathematical Society Publishing House,2006∶1433-1452.

[4]程艳合，杨文革.利用基字典构造的直扩测控信号稀疏性分析[J].信号处理，2015,31(5)∶594-601.

[5]SEUNG-HYUM K.A deterministic compressed GNSS acquisition technique[J].IEEE Transactions on Vehicular Technology, 2013,62(2)∶511-521.

[6]单建华，张晓飞.稀疏表示人脸识别的关键问题分析[J].安徽工业大学学报(自然科学版)，2014,31(2)∶188-193.

[7]程艳合，杨文革.压缩域直扩测控通信信号伪码跟踪方法研究[J].电子与信息学报，2015,37(8)∶2028-2032.

[8]康荣宗，于宏毅，田鹏武，等.基于压缩感知的自适应干扰抑制算法[J].吉林大学学报(工学版)，2012,42(6)∶1587-1591.

[9]张永顺，贾鑫，尹灿斌.基于压缩感知的直扩通信多音干扰抑制[J].电讯技术，2015,55(8)∶848-853.

[10]田日才.扩频通信[M].北京：清华大学出版社，2012∶6-7.

[11]KAZUNORI H,MASAAKI N,TOSHIYUKI T.A user’s guide to compressed sensing for communications systems[J].IEICE Transactions on Communications,2013,96(3)∶685-712.

[12]XIA S,LIU Y,SICHINA J,et al.A compressive sensing signal detection for UWB radar[J].Progress in Electromagnetics Research,2013,141(4)∶479-495.

[13]马宏，秦国领，魏绍杰.基于熵权的DS/FH测控系统抗干扰效能评估指标赋权研究[J].遥测遥控，2015,36(4)∶58-63.

[14]秦国领.DS/FH测控系统抗干扰效能评估技术研究[D].北京：装备学院，2014∶33-36.

[15]路伟涛.DS/FH混合扩频测控体制抗干扰性能研究[D].北京：装备学院，2010∶47-49.

责任编辑：何莉

Jamming Suppression Algorithm of Direct Sequence Spread Spectrum TT&C Signal Based on Compressed Domain

QIN Guoling，WU Xiaodong，ZHANG Haiqi，NIU Panfeng
(Jiuquan Satellite Launch Center,Jiuquan 732750,China)

Compressed sensing theory breaks the bondage of classical sampling theory,and effectively eases the signal processing and data storage pressure of direct sequence spread spectrum(DS)telemetry tracking and command(TT&C)signals in large bandwidth sampling.After analyzing the difference between DS TT&C and jamming signals,an adaptive jamming suppression algorithm of DS TT&C signals based on compression domain was proposed.Based on the feature of DS TT&C signals,corresponding sparse matrix was built.The normalized residual and relevant change rule of DS TT&C signals and jamming signal in the sparse matrix were computed and validated,DS TT&C signals were reconstructed with sparse coefficient,and the adaptive control of algorithm was achieved combined with change rate of normalized residual.Simulation results show that the algorithm can effectively restrain jamming signals,and detection probability and bit error rate respectively increased by 3 dB and 2 dB compared with those of the direct treatment.

compressed sensing;DS TT&C signal;jamming suppression;compressed domain

TN 914.4

A

10.3969/j.issn.1671-7872.2016.03.018

2016-04-07

秦国领(1990-)，男，河南周口人，工程师，主要研究方向是航天测控和信号处理。

1671-7872(2016)03-0295-07