一种结合GVF和CV模型的水平集图像分割方法
胡小为,刘宏申,徐国雄,阮 越,刘 恒,潘 祥
(安徽工业大学计算机科学与技术学院,安徽马鞍山243032)
一种结合GVF和CV模型的水平集图像分割方法
胡小为,刘宏申,徐国雄,阮 越,刘 恒,潘 祥
(安徽工业大学计算机科学与技术学院,安徽马鞍山243032)
由于CV(Chan-Vese)模型是一个非凸性泛函,对该泛函求极值只能得到局部最优解,运用该模型进行图像分割时,很难在全局范围内得到理想的结果。鉴于此,提出一种结合梯度矢量流(gradient vector flow,GVF)和CV模型的水平集图像分割方法。该方法通过GVF将边缘梯度信息扩散至整幅图像,在保留CV模型基本优点的同时,融入GVF的全局性梯度信息,从而引导CV模型在全局范围内演化至准确的目标边缘。实验结果表明,该方法的分割效果和收敛速度均明显优于传统CV模型。
图像分割;水平集方法;CV模型;梯度矢量流
近20年以来,基于曲线演化理论和偏微分方程图像分割方法取得了一系列的研究成果[1-4],尤其是结合Osher等[5]于1988年提出的水平集算法,为此类分割方法提供了有效的数值解方法。CV模型是一种利用水平集算法进行数值解的图像分割模型,由于其可以有效分割含噪声和弱边缘图像,受到了国内外学者的广泛关注。
MS模型是Mumford等[6]提出的一种基于区域信息的分段光滑分割模型。该模型将图像分割和目标平滑结合在一起,是一种较为理想的分割模型,但是该模型的数值解计算复杂。针对该问题,Chan等[7]提出一种基于精简MS模型的分段常数分割模型,即CV模型。CV模型对图像进行二相位分割,分割过程中对目标和背景的灰度值进行常数项拟合,由于完全不依赖于图像的边缘梯度信息,该模型对含噪声和弱边缘图像具有较好的分割效果,并且在数值解过程中引入了水平集算法,使得该模型的数值解计算方便。但是在实际应用中,CV模型也有其自身的缺陷,主要表现在两个方面:(1)该模型把图像分为目标和背景两个区域,并进行常数项拟合,得到二相位的分段常数图像,因而不能直接分割多相图像,该问题已有学者提出了一系列有效的解决方案[8-11];(2)由于CV模型是一个非凸性泛函,因此很难得到该泛函的全局最优解。针对这类问题,文献[12]中提出将ROF(Rudin-Osher-Fatemi)去噪模型和CV模型结合起来,并对能量泛函中的非凸特征函数进行扩展,由于ROF是全局凸模型,使得原本的非凸泛函极小化问题转变为凸泛函的极小化问题,该方法的缺点是分割结果严重依赖初始条件的设定;文献[13]中提出利用K-means算法在每一次迭代过程中计算轮廓的内部和外部,利用全局性聚类结果不断对CV模型的分割结果进行修正;但是文献[13]中也指出该方法只是优化了CV模型的分割结果,并不能保证每一次得到全局性的分割结果。
针对CV模型的第2个缺陷,本文提出一种结合GVF和CV模型的水平集图像分割模型,首先利用GVF将局部的边缘梯度扩散为全局的梯度矢量场,然后将该全局梯度信息和传统CV模型结合起来,并纳入能量泛函,从而引导CV模型进行全局性的演化。由于添加了全局梯度信息,使得水平集函数的演化速度大大提高,从而有效减少CV模型的收敛时间和迭代次数。
1 CV模型的原理及分析
设Ω为待分割图像区域,u0(x,y)为原始图像(x,y)处的灰度值,C为自定义的活动轮廓曲线,Ω1为曲线内部区域,Ω2为曲线外部区域,c1为曲线内部像素灰度的平均值,c2为曲线外部像素灰度的平均值,CV模型定义为如下泛函

其中:μ为控制长度项的权重系数;ν为控制面积项的权重系数;λ1和λ2为控制轮廓内部和外部灰度拟合项的权重系数。该泛函的第1项为长度项,L(C)表示活动轮廓的长度,要求活动轮廓C的长度尽可能短;第2项为面积项,S(C)表示活动轮廓的内部面积,要求活动轮廓C的内部面积尽可能小。第1项和第2项的作用是使活动轮廓C尽可能收缩且平滑;第3项和第4项为轮廓内部和外部的灰度拟合项,要求分割结果为分段常数图像且该分段常数图像与源图像尽可能相似。通过求该泛函的极小解,即可得到满足该泛函条件的最终活动轮廓C,再对C的内部和外部求像素平均值,就可以得到与原图像对应的分段常数图像,即CV模型的分割结果。
水平集是一种隐式表达曲线演化问题的数值解方法[5],其基本原理是将演化曲线表达为水平集函数的零水平集,从而实现由低维平面的曲线演化问题转化为高维空间的曲面演化问题。与曲线演化相比,水平集演化可以很自然地表达曲线在演化过程中的拓扑结构变化。先定义Heaviside函数H(z)及其Dirac测度δ(z)

利用该Heaviside函数及其Dirac测度可以将能量泛函(1)改写为以水平集函数φ表示的形式

其中:Ω为图像区域;∇为梯度运算符。将Heaviside函数及其Dirac测度正则化为
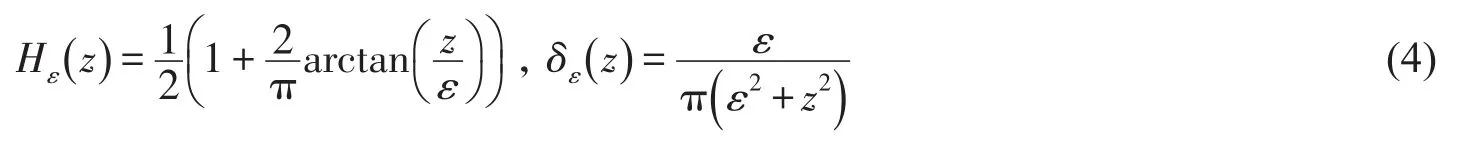
引入时间变量t并利用变分法可以得到式(3)的梯度下降流为

其中div为散度运算符。利用有限差分法可对式(5)进行离散化并求其数值解。
针对CV模型分割结果严重依赖初始活动轮廓位置的问题,李俊等在文献[14]中提出将式(5)中的δε(φ)替换成|∇φ(x,y)|,从而其梯度下降流变为

这一替换在一定程度上提高了水平集函数的演化速度和迭代步长,扩大了活动轮廓的“捕获”范围,但实验结果表明,这种优化并非是全局性的,如果目标边缘与活动轮廓距离过远,则该方法并不能进行有效的全局分割(图2(c))。
2 CV模型的改进
从曲线演化的角度看,传统CV模型不能进行全局性分割的原因在于模型本身缺少表示全局信息的变量,每一次演化过程都局限于局部范围。梯度矢量流[15](gradient vector flow,GVF)是一种对目标边缘梯度进行全局扩散而产生的静态矢量场,它的分布仅依赖于原始图像目标边缘,而与曲线演化过程中的其他变量无关,可用于解决参数活动轮廓模型无法收敛至深度凹陷边缘的问题。
2.1 梯度矢量流
为了得到GVF,通过式(7)对原始图像u0(x,y)进行边缘映射,得边缘映射图像f(x,y)

其中:Gσ(x,y)是标准差为σ的二维高斯函数;∗为卷积运算符。设梯度矢量流V(x,y)=[m(x,y),n(x,y)],其能量泛函为

其中η为规则化参数,η值根据图像中噪声强弱选择,噪声强烈增加η值,反之则减少η值。可以看出,在图像的匀质区域(|∇f|值较小),该能量泛函的值主要由第1项决定,产生的扩散矢量场变化缓慢。在目标边缘处(|∇f|值较大),该能量泛函的值主要由第2项决定,梯度矢量流V(x,y)=∇f,利用变分法,求得该泛函的Euler-Lagrange方程组

其中∇2为拉普拉斯算子。最后利用有限差分法对式(9)进行离散化,得到数值解,具体过程见文献[15]。
2.2 结合GVF的改进CV模型
针对传统CV模型存在的局部最优解问题,结合GVF的全局性信息,本文提出一种改进的CV模型

此式在式(1)的基础上添加最后一项,前4项的作用与式(1)中相同。其中:,V(x,y)为图像的梯度矢量流;γ为梯度吸引项的权重系数。添加项为边缘梯度吸引项,利用GVF将边缘梯度信息扩散至全局范围,其主要作用是引导活动轮廓收敛至边缘梯度值最大处,即目标边缘。在图像的非目标边缘区域,|V(x,y)|值较小,函数项g值较大;在图像的目标边缘,|V(x,y)|值较大,函数项g值较小。运用该模型进行图像分割时,收敛过程朝着泛函极小值的方向进行,最终停留在g值较小(|V(x,y)|值较大)的目标边缘处,由于该边缘梯度信息是全局性的,所以厚壁内部边缘、距离活动轮廓较远的目标边缘均可对活动轮廓的演化产生吸引作用,从而引导活动轮廓收敛至全局最优解。
同样对式(10)采用变分水平集方法引入水平集函数φ和时间变量t,利用变分法得到梯度下降流
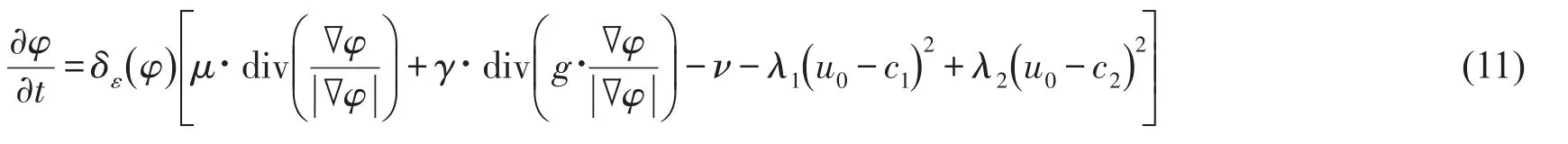
2.3 改进模型的数值解
能量泛函的梯度下降流本质是一个偏微分方程,求其解析解十分困难,因此本文利用有限差分法来离散化能量泛函的梯度下降流,求其数值解。可以用离散网格来表达水平集函数φ(x,y,t),设h为离散网格的空间间隔,Δt为迭代的时间间隔,则在n时刻,网格点(i,j)处的水平集函数。将初始水平集函数φ定义为活动轮廓C的符号距离函数(signed distance function,SDF),即φ(x,y,t=0)=d(x,y),其中d(x,y)表示图像中点(x,y)到活动轮廓C的符号距离,在C内部取正值,在C外部取负值,在C上取零值。记差分:
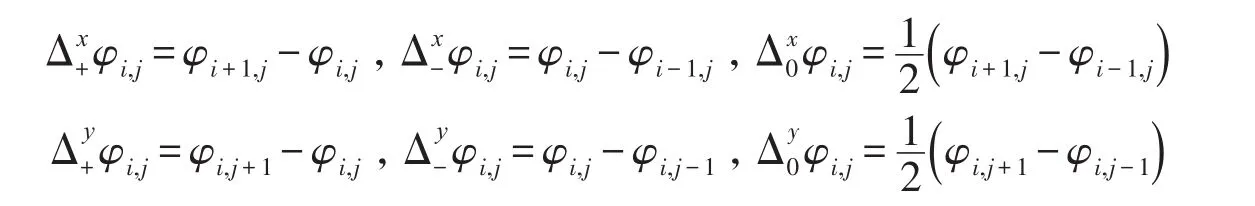
根据文献[16-18],为了避免水平集函数的重新初始化和保持水平集函数的稳定性,选用有限差分半隐式方案进行偏微分方程的数值化计算,得离散化的迭代式(12)。

初始化水平集函数φ和参数 μ,ν,λ1,λ2,γ,Δt及h,对上式进行迭代计算直至分割结果趋于稳定,此时的活动轮廓C={(x,y)|φ(x,y,t)=0}即为最终的目标轮廓。
3 实验结果及分析
为了验证上述改进模型的可行性和有效性,通过实验对本文改进模型(记作GVF-CV)与传统CV模型及李俊改进的CV模型(记作Li-CV)在收敛时间、迭代次数以及收敛结果3个方面进行比较。实验在CPU为Core 2.13 GHz、内存为2G的硬件平台上利用VC++6.0编程实现,参数取 μ=0.2,ν=0.2,λ1=λ2=1,γ=0.2,Δt=0.1,h=1。以3组具有代表性的实验来分析3种模型的性能。
实验1针对含噪声厚壁环状图像,分割结果如图1。图1中,初始轮廓在目标外围。使用传统CV模型无法分割出厚壁内部边缘,Li-CV模型和GVF-CV模型均可实现有效分割,但是GVF-CV模型在收敛时间和迭代次数2个方面要优于Li-CV模型,见表1。

图1 含噪声厚壁环状图像分割结果Fig.1 Segmentation results of thick walled ring image with noise
实验2针对含噪声多目标图像,分割结果如图2。图2中,初始轮廓包含部分目标。使用传统CV模型和Li-CV模型均只能分割部分目标,而使用GVF-CV模型可以实现有效的全局分割,且收敛时间和迭代次数均优于传统CV模型和Li-CV模型,见表1。
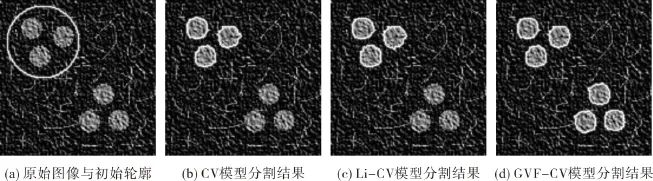
图2 含噪声多目标图像分割结果Fig.2 Segmentation results of multi-target image with noise
实验3针对无噪声多目标图像,分割结果如图3。图3中,初始轮廓在两个目标之间。由于初始轮廓距离内部目标较远,传统CV模型和Li-CV模型均只能分割外部目标,而使用GVF-CV模型分割的结果要优于传统CV模型和Li-CV模型,见表1。

图3 无噪声多目标图像分割结果Fig.3 Segmentation results of multi-target image without noise
由图1~3可以看出,模型的改进对不同状况图像分割结果均有明显改善。从表1中可以看出,本文的GVF-CV模型的收敛时间、迭代次数以及收敛结果均优于传统CV模型和Li-CV模型。
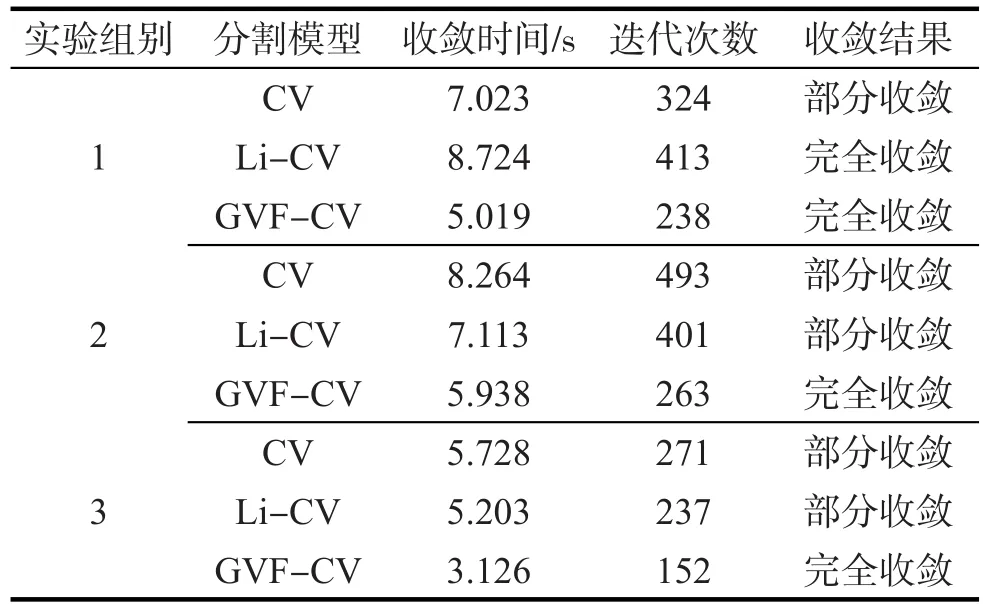
表1 3种模型的性能比较Tab.1 Performance comparison of three models
4 结 语
传统CV模型是非凸性泛函,其数值解难以在全局范围内收敛至最优。针对这个缺陷,本文将GVF和传统CV模型结合起来,利用GVF将局部边缘梯度信息扩散至全局区域,并在CV模型中添加边缘梯度吸引项,从而引导活动轮廓收敛至正确的目标边缘。实验结果表明,本文方法在收敛速度、迭代次数及分割效果等方面均明显优于传统CV模型分割方法,其保留了传统CV模型可以有效分割含噪声图像的优点,且提高了对多目标图像的分割能力。本文改进CV模型的不足之处在于:如果图像噪声过于强烈且目标边缘过于虚弱,则会影响GVF的分布,从而降低该模型的分割效果。这是后续工作将要研究解决的一个问题。
[1]WEICKERT J.Efficient image segmentation using partial differential equations and morphology[J].Pattern Recognition,2001, 34(9)∶1813-1824.
[2]刘利雄,马忠梅,赵恒博.一种基于主动轮廓模型的心脏核磁共振图像分割方法[J].计算机学报,2012,35(1)∶146-153.
[3]KAUR J,AGRAWAL S,VIG R.Integration of clustering,optimization and partial differential equation method for improved image segmentation[J].International Journal of Image,Graphics and Signal Processing(IJIGSP),2012,4(11)∶26-33.
[4]NIANG O,THIOUNE A,GUEIREA M C E.Partial differential equation-based approach for empirical mode decomposition∶application on image analysis[J].Image Processing,IEEE Transactions on,2012,21(9)∶3991-4001.
[5]OSHER S,SETHIAN JA.Fronts propagating with curvature dependent speed∶algorithms based on Hamilton-Jacobi formulations [J].Journal of Computational Physics,1988,79(1)∶12-49.
[6]MUMFORD D,SHAH J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications on Pure andApplied Mathematics,1989,42(5)∶577-685.
[7]CHAN T F,VESE LA.Active contours without edges[J].Image Processing,IEEE Transactions on,2001,10(2)∶266-277.
[8]VESE L A,CHAN T F.A multiphase level set framework for image segmentation using the Mumford and Shah model[J].International Journal of Computer Vision,2002,50(3)∶271-293.
[9]GAO S,BUI T D.Image segmentation and selective smoothing by using Mumford-Shah model[J].Image Processing,IEEE Transactions on,2005,14(10)∶1537-1549.
[10]CHUNG G,VESE L A.Image segmentation using a multilayer level-set approach[J].Computing and Visualization in Science, 2009,12(6)∶267-285.
[11]LIU S,PENGY.Alocal region-based Chan-Vese model for image segmentation[J].Pattern Recognition,2012,45(7)∶2769-2779.
[12]CHAN T F,ESEDOGLU S,NIKOLOVA M.Algorithms for finding global minimizers of image segmentation and denoising models[J].SIAM Journal onApplied Mathematics,2006,66(5)∶1632-1648.
[13]BROWN E S,CHAN T F,BRESSON X.Completely convex formulation of the Chan-Vese image segmentation model[J].International Journal of Computer Vision,2012,98(1)∶103-121.
[14]李俊,杨新.基于Mumford-Shah模型的快速水平集图像分割方法[J].计算机学报,2002,25(11)∶1175-1183.
[15]XU C,PRINCE J L.Snakes,shapes,and gradient vector flow[J].Image Processing,IEEE Transactions on,1998,7(3)∶359-369.
[16]LI C,XU C,GUI C.Level set evolution without re-initialization∶a new variational formulation[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[s.l.]∶IEEE,2005,1∶430-436.
[17]SMEREKA P.Semi-implicit level set methods for curvature and surface diffusion motion[J].Journal of Scientific Computing, 2003,19(1)∶439-456.
[18]KOLAHDOUZ E M,SALAC D.A semi-implicit gradient augmented level set method[J].SIAM Journal on Scientific Computing,2013,35(1)∶A231-A254.
责任编辑:丁吉海
ALevel Set Image Segmentation Method Combined with GVF and CV Model
HU Xiaowei,LIU Hongshen,XU Guoxiong,RUAN Yue,LIU Heng,PAN Xiang
(School of Computer Science and Technology,Anhui University of Technology,Ma'anshan 243032,China)
Owning to the non-convex functional of with the Chan-Vese(CV)model,one can only obtain a local optimal solution.It is difficult to achieve an ideal result for image segmentation in the global range.Therefore a new level set based image segmentation method that combining CV model and gradient vector flow(GVF)was proposed.The edge gradient information is spreaded to the entire image with GVF,which guides the evolution of CV model to the correcttarget edge in the global range and retains the basic advantages of CV model.The experimental results indicate that the present method are obviously better than the traditional CV model.
image segmentation;level set method;CV model;gradient vector flow
TP 391.41
A
10.3969/j.issn.1671-7872.2016.03.017
2015-11-10
安徽省自然科学基金项目(1308085QF113)
胡小为(1989-),男,安徽安庆人,硕士生,研究方向为图像处理。
刘宏申(1962-),男,安徽宣城人,教授,研究方向为图像处理与模式识别。
1671-7872(2016)03-0289-06

