水库突发性污染事故水质影响过程分析

张 琳,孙 娟,翟家佳,颜芬芬,张 奕

(1.长江科学院 河流研究所，武汉 430010；2.南京大学 金陵学院，南京 210089；3.河海大学 环境学院，南京 210098)



水库突发性污染事故水质影响过程分析

张 琳1,孙 娟2,翟家佳3,颜芬芬3,张 奕3

(1.长江科学院 河流研究所，武汉 430010；2.南京大学 金陵学院，南京 210089；3.河海大学 环境学院，南京 210098)

为了有效地控制突发性水污染事故带来的危害，以东北某大型水库为典型研究案例，综合考虑水库水文、气象条件和污染物迁移特征，拟定典型工况，基于已建立的三维水动力和水质耦合模型，模拟分析突发性污染事故发生后库区污染物三维空间分布及随时间变化的特征。结果表明：受入库流量和全年主导风向东北风的影响，总体上污染物随着水流沿西南岸线向坝址方向扩散，且污染物的超标面积逐渐增大；但随着流程的增加，污染物的浓度逐渐减小。通过对水库水质的数值模拟，定量掌握了水库水质实时状态以及污染物空间分布，可以为有关部门制定与实施应急预案提供相关的技术依据。

突发性水污染事故；水质；水库；污染物三维空间分布；三维数值模拟

1 研究背景

近年来，突发性水污染事故在我国重点流域频繁发生，由于其发生的不确定性、处理处置的艰巨性、水污染信息的不完整性与不可比性等特点，往往对水环境安全造成重大威胁[1]。为了预防和控制潜在的水环境风险，准确预测水体中污染物的迁移和扩散情况非常必要[2-3]。

随着水质模型研究的深入，国际上已经有很多成熟的水质模型软件[4]，然而这些模型输入参数多，分析工作量大，对于突发性水污染事故风险预测难度较大。本文针对大中型水库水动力及污染物迁移扩散特征，采用以N-S方程为基础的紊流运动方程和物质输运方程建立三维水动力[5]和水质耦合模型[6-7]，能够快速获取数据，快速模拟污染团的迁移轨迹和空间分布[8]，实时预报校正，为有关部门制定与实施应急预案提供科学依据，对于制定切实可行的应急措施，有效控制事故的危害，具有重要的技术支撑作用。

2 三维水动力模型数学描述

2.1 三维水动力数学模型

笛卡尔坐标系下描述水库三维水流运动的控制方程组[9-10]如下：

(1)

(2)

(3)

(4)

2.2 三维水质数学模型

笛卡尔坐标系下污染物三维输运方程为

(5)

式中：C为污染物浓度；K为污染物衰减系数；Dv为垂向扩散系数；Dk为水平扩散系数。

3 三维水动力及水质模型验证

3.1 水动力数值模拟验证

3.1.1 明渠恒定流垂向流速分布

选用指数律流速分布经验公式[11]来验证数值模拟的结果。设计试验明渠长5 000 m，宽600 m，水深10 m，东、西边界分别为上、下游边界。将水体流动稳定后的中心断面模拟结果与根据垂向流速指数律分布公式计算的结果对比进行模型验证，结果见图1。经统计，数值解与解析解的绝对误差范围为-0.015～0.003 1 m/s，相对误差范围为-11.86%～1.23%，模型较好地模拟了明渠水流的流速分布。

图1 水动力数值模拟验证结果Fig.1 Verification results of numericalhydrodynamics simulation

3.1.2 矩形水槽内风生环流分布

本文选用封闭矩形水槽内静止水体在风应力的作用下引起的回流对模型进行验证。设计试验水槽长1 000 m，宽100 m，水深10 m，垂向分20层，垂向紊动黏性系数取定值0.012。

底部为无滑移边界条件，水面风应力为恒定，忽略对流、哥氏力和水平扩散的作用情况下，流速垂向分布解析解为[12]

(6)

式中：u为水平流速(m/s)；σ为相对水深；KM为垂向紊动黏性系数；τ为均匀风应力；D为总水深。

均匀风应力计算公式为

(7)

式中：ρa为空气密度；C为风的拖拽系数；U，V分别为风速在x，y方向的分量。

稳定状态下，中心断面垂向流速分布及其与解析解的对比见图2。经统计，数值解与解析解的绝对误差范围为-0.005～0.015 m/s，相对误差范围为-9.59%～14.72%，模型较好地模拟了矩形水槽风生环流水平流速的垂向分布。

图2 矩形水槽内水动力验证结果Fig.2 Verification results of hydrodynamics simulation in rectangular flume

3.2 水质数值模拟验证

通过理想水槽点源物质输移扩散数值模拟与恒定状态下非保守物质连续排放的三维对流扩散方程解析解的比较，验证水质数学模型的准确度与精度。设计试验水槽长10 000 m，宽5 000 m，水深20 m，垂向分10层。东、西边界分别为上、下游边界。合理设置边界条件，保证水槽内为恒定均匀流，污染物排放为连续排放，排污口位于第5层。模拟足够长时间，取y=2 500，第5层M水平线为纵向对比线；以排污口为原点，取过点 (1 000，0)的N垂线上的水质分布作对比垂线。对比结果见图3，数值解与解析解基本吻合，可见，模型能较好地模拟非保守污染物的输运过程。

图3 水质数值模拟验证结果Fig.3 Verification results of numerical water quality simulation

4 基于三维数值模型的库区污染物浓度变化特征分析

大伙房水库位于辽宁省东北部，是中国第一个五年计划中的第一个大型水库，是沈阳、抚顺2市居民的重要饮用水源地。S202和G1212两条公路从大伙房水库浑河入库区域北侧经过，最近点距大伙房水库83 m，车辆泄漏的危险载运物品有可能流入大伙房水库，因此选取附近水域为突发性事故风险源研究水域。具体位置如图4所示。

图4 水污染事故研究区域Fig.4 Research area of pollution accident

大伙房水库最大水深达41.5 m，属于深水库，流速、污染物浓度沿垂向分布差异较大，因此综合考虑水库水文、气象条件和污染物迁移特征[13]，选取水库实测多年平均入库流量作为水流边界条件[14]，以常年平均风速2.3 m/s和主导风向(NE)作为自由表面条件[15]，垂向上采用等距离分层进行剖分，共分为7层，建立水库三维水动力、水质模型模拟分析突发性污染事故后库区污染物三维空间分布及随时间变化的特征。

参照货车载重量，源强取为20 t，污染因子为苯酚，假定污染物瞬时排入库区。

图5 水平流场分布Fig.5 Distribution of horizontal flow fields

4.1 参数取值

水平涡黏系数采用Smagorinsky亚网格尺度紊动模型计算，cs取值为0.28；垂向涡黏系数采用Kolmogorov-Prandl求解，其中k和ε通过求解k-ε方程可以得到；底部粗糙高度取决于底部局部粗糙程度，在缺乏相关资料的情况下，通常取为0.002～0.01 m，根据相关研究，本文取值为0.01 m。风速选取为春季平均风速3 m/s(NE)。

紊动扩散系数是影响污染物扩散的主要因素之一，它是由于水流的紊动造成的扩散，紊动扩散与涡黏系数的比例因子由1/σT估算，σT为施密特数，取1.0。参考相关文献，苯酚的衰减系数取为0.05/d。

4.2 三维水动力特征分析

4.2.1 水平流场特征

在模型计算达到稳定状态时，取库区自由水面层(表层)，第4层(中层)及床面层(底层)的水流流态进行分析。

如图5所示，水体流向基本为自浑河入库口向坝址处流动，表现出良好的顺岸流特征，库区岸边相对中部水深较深处流速明显变大，平均流速约为0.045 m/s。来自上游浑河、苏子河的水流，一部分流向坝址，一部分流向社河的入库口，与从社河流入水库的水流形成顺时针的大环流。中层水体水流结构与表层水体呈现相似的水动力特征，水体流向基本为自浑河入库口向坝址处流动，受上游来流的影响，浑河、苏子河入库口区域流速较大，在来自上游浑河、苏子河的水流与从社河流入水库的水流共同作用下，社河入库口区域形成顺时针的大环流。库区中段卡口处，水流受弯道和地形的影响形成一个顺时针方向的环流。水库底部水流结果较为复杂，来自上游浑河、苏子河的水流，一部分流向坝址，一部分流向社河的入库口，与从社河流入水库的水流形成顺时针的大环流，来自社河的水流一部分流向坝址处，一部分在补偿作用的影响下，向上游流动，与从浑河、苏子河向下游流动的水流在水库凹岸处形成一个顺时针方向的环流。

4.2.2 垂向流场特征

选取断面1、断面2、断面3分别对水库入库口、水库库区中段、水库坝址处的垂向流场进行分析。断面上流速矢量分布如图6所示。

图6 各断面垂向流速分布Fig.6 Distribution of vertical velocity in different sections

由图6可知，水库入库区域流速在垂向上存在较大梯度，表现为从表层向底层流速大小依次递减；纵向流场分布形态与河床地形形态相似，水流流态受地形影响明显，与地形变化趋势吻合，在地形变化急剧的地方出现局部垂向分量较大的情况。库区中段上游部分垂向水流结构表现为以吞吐流为主的水动力特征，水流方向总体上自上游向坝址处流动，流场分布形态与河床地形形态相似，水流流态受地形影响明显，与地形变化趋势吻合，流速大小呈现从表层向底层依次递减的规律；库区中段下游部分表层至中层水流结构表层为以吞吐流为主的水动力特征，流速大小从上层至下层逐渐减小，中层至底层水流结构表现为以补偿流支配为主的水动力特征，流速大小从上层至下层逐渐增大。断面3垂向流场空间分布较规则，总体上呈现以吞吐流支配为主的水动力特征，水流方向为自上游向坝址处流动，流速大小从表层向底层逐渐减小，在坝址处，受出水口位置的影响，水流出现向上的流速。

4.3 污染物浓度变化特征分析

4.3.1 平面分布特征分析

水平方向上，取自由水面层(表层)，第4层(中层)及床面层(底层)的苯酚分布状态进行特征分析。苯酚最大超标范围(浓度>0.02 mg/L)包络线几何参数见表1，图7为事故发生后不同时刻苯酚表层浓度场分布。

表1 不同时刻污染物浓度超标范围

如图7所示，污染物为岸边排放，在水流输移作用下，随着时间的推移，污染团沿东北岸随流运动，至环流区受环流影响，污染团随之环向扩散，但受水体剪切分散的影响，污染团整体仍向坝址方向移动。在此过程中污染团超标范围(浓度>0.02 mg/L)的面积也逐渐扩大至最大范围然后减小，在事故发生57 h后超标面积最大，表层最大值为3.07 km2，中层为3.09 km2，底层为3.11 km2。由表1可知，各层污染团超标范围面积相差不大，接近垂向均匀混合状态。

图7 不同时刻污染物表层浓度场Fig.7 Surface concentration fields of contaminants at different moments

4.3.2 纵向立面分布特征分析

垂向方向上，取事故点垂线断面不同时刻浓度分布进行分析。苯酚泄漏进水体，在10 min后即垂向混合均匀，浓度场垂向分层明显，5 h后事故点垂线位置苯酚浓度属于达标状态(<0.02 mg/L)。事故点苯酚浓度垂向分布见图8。

图8 事故点不同时刻纵向立面浓度场Fig.8 Facades of vertical concentration fields at the accident site at different moments

在事故点下游距事故点直线距离分别为1 200，1 500，1 800 m的位置设定监测点S1，S2，S3。监测点位置见图4。图9为事故发生5 d内监测点S1，S2，S3的浓度变化曲线。

图9 风生流表层监测点浓度曲线Fig.9 Curves of concentration at monitoring points on the surface of wind-driven current

由图9可知，事故发生后0.5 h左右，苯酚污染团即扩散到S1点，S1点的浓度随即上升，在4 h左右达到浓度最大值0.84 mg/L，随后浓度值降低，由于受到环流的影响，上游受污染的水体运动至S1点，因此在19 h时浓度达到最小极值后出现小幅度的上升，在50 h时左右浓度达到一定极值后再下降至对水质无影响；事故发生后2 h左右，苯酚污染团扩散至S2点，S2浓度随即上升，在7h时浓度达到最大值0.42 mg/L，由于该监测点水流结构呈现以吞吐流为支配的水动力特征，因此在对流输移与水体紊动剪切分散作用下，污染物的浓度值逐步降低至对水质几乎没有影响；S3点水流结构与S1相似，因此该监测点浓度随时间变化规律大体同于S1，受地理原因影响，苯酚污染时间发生相应延迟。因污染物的对流输移和水体紊动剪切分散作用，污染团中心浓度沿程减小，S2点的最大污染浓度小于S1，S3点小于S2。 图10为S2不同时刻横向立面浓度场分布，图11为S2和S3两点连线垂向断面不同时刻垂向浓度场分布。

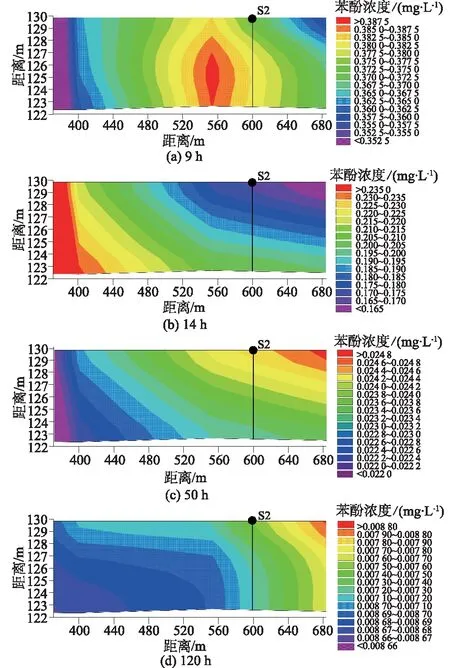
图10 S2不同时刻横向立面浓度场Fig.10 Facades of transverse concentration fields at monitoring point S2 at different moments

图11 S2-S3不同时刻纵向立面浓度场Fig.11 FacadesoflongitudinalconcentrationfieldsatmonitoringpointS2andS3atdifferentmoments

如图10、图11所示，在事故发生9 h时，污染团中心移动至S2点，S2-S3断面苯酚浓度开始急速上升，至50 h时，S2苯酚浓度达标，在此过程中，因断面垂向流速梯度较大，苯酚浓度垂向均匀混合，垂向分层明显。在120 h后，全断面均达标(浓度<0.02 mg/L)。

模拟结果显示，随着污水团不断向下游迁移，污水团中心可溶性污染物浓度沿流程逐渐减小。水流结构是影响断面纵向立面浓度场随时间变化特征的重要因素，当断面水流结构呈现以风生环流为支配的水流特征时，浓度变化呈现从无影响→受到影响→影响增加→达到峰值→逐步衰减→再次影响(影响较小)→影响消失的过程；当水流结构呈现以风生环流为支配的水流特征时，浓度变化呈现从无影响→受到影响→影响增加→达到峰值→逐步衰减→影响消失的过程。

5 结 语

针对大中型水库水动力及污染物迁移扩散特征，采用以N-S方程为基础的紊流运动方程和物质输运方程建立三维水动力和水质耦合模型。以东北某大型水库为典型研究案例，该模型有效地模拟了大伙房水库突发性污染事故发生后库区污染物三维空间分布及随时间变化的特征。模拟结果表明，受入库流量和全年主导风向东北风的影响，总体上污染物随着水流沿西南岸线向坝址方向扩散，且污染物的超标面积逐渐增大，但随着流程的增加，污染物的浓度逐渐减小。水流结构是影响断面纵向立面浓度场随时间变化特征的重要因素，当断面水流结构呈现以风生环流为支配的水流特征时，浓度变化呈现从无影响→受到影响→影响增加→达到峰值→逐步衰减→再次影响(影响较小)→影响消失的过程。该模型的建立，完善了水库水污染应急反应体系，在一定程度上间接提高了水污染事故应急反应的水平。

[1] 沈永明,郑永红,吴修广.近岸海域污染物迁移转化的三维水质水动力学模型[J].自然科学进展,2004,14(6):694-699.

[2] 侯国祥，翁立达，叶 闽,等.三峡水库重庆库区水质预测[J].长江科学院院报,2002,19(1):13-16.

[3] 唐建华，刘玮祎，陶 静,等.长江口北支倒灌对南支水域水质影响初探[J].长江科学院院报,2012,29(9):14-17.

[4] 黎育红，贺石磊.浅水湖泊群联通与调水的二维水动力-水质耦合模型研究[J].长江科学院院报,2015,32(1):21-27.

[5] DAVYDOV B I. On the Statistical Dynamics of an Incompressible Turbulent Fluid[J]. Soviet Physics Doklady,1961, 4: 769.

[6] 韩龙喜，陆东燕，李洪晶，等.高盐度湖泊艾比湖风生流三维数值模拟[J].水科学进展,2011,22(1)：97-103.

[7] HARLOW F H, NAKAYMA P I. Transport of Turbulence Energy Decay Rate[R]. US: Los Alamos Scientific Lab., 1968.

[8] 张防修,王艳平,刘兴盛,等.黄河下游突发性污染事件数值模拟[J].水利学报,2007,(增刊):613-618.

[9]SPALDING D B. The Prediction of Two-dimensional Steady Turbulent Flows[R]. London: Heat Transfer Section, Imperial College, 1969.

[10]UNESCO. Tenth Report of the Joint Panel on Oceanographic Tables and Standards[J]. UNESCO Technical Papers in Marine Science,1981, (36): 17-21.

[11]黄才安. 明渠流速分布指数律与对数律的统一及转换[J]. 人民长江,1994,25(1)：42-44.

[12]KOUTITAS C, O’CONNOR B. Modeling Three-dimensional Wind-induced Flows[J]. Journal of Hydraulic Division, ASCE, 1980，106(11)：1843-1865.

[13]黄 瑞,张防修,孙 娟,等. 大伙房水库监测断面水质特征分析[J].水科学与工程技术, 2012,(1):78-81.

[14]张 静，何俊仕. 大伙房水库汛期气象水文特征分析[J]. 人民黄河, 2012, 34(11):45-47.

[15]白玉良，贺国静，吴玉禾. 大伙房水库环境水文气象效应[J]. 水利管理技术,1994, (3):35-37.

(编辑：姜小兰)

Numerical Simulation on the Process of Water Quality Influenced bySudden Pollution Accident of Reservoir

ZHANG Lin1, SUN Juan2, ZHAI Jia-jia3, YAN Fen-fen3, ZHANG Yi3

(1.River Department, Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.Jinling College, Nanjing University, Nanjing 210089, China; 3.College of Environment, Hohai University, Nanjing 210098, China)

To prevent from and control the effect of emergent water pollution accident in reservoir area, the temporal and spatial variations of pollutants in the reservoir after the accident were simulated by a 3-D model coupling hydrodynamics and water quality at typical working conditions. Factors of hydrology, meteorology and contaminant move-ment were taken into account. A large reservoir in the northeastern area of China was taken as a case study. Results revealed that affected by inflow and dominant wind in northeast direction, the contaminants spread toward the direction of the dam site along the southwest coastline, and the area of standard-exceeding contaminants increased gradually; but the concentration of contaminants decreased gradually with the flow process. Through simulation of the water quality, the spatial distribution of contaminants is quantitatively obtained, which offers technical basis for emergency treatment.

emergent water pollution accident; water quality; reservoir; spatial distribution of contaminants; 3-D numerical simulation

2014-08-26；

2015-10-20

张 琳(1988-)，女，福建三明人，工程师，硕士，主要从事环境水力学研究，(电话)15342788110(电子信箱)zlincandy@163.com。

10.11988/ckyyb.20140746

2016,33(10):12-17,23

X24

A

1001-5485(2016)10-0012-06