基于Pareto支配的MPRM电路面积与可靠性优化
卜登立,江建慧
(1.井冈山大学电子与信息工程学院,江西吉安 343009; 2.同济大学软件学院,上海 201804; 3.流域生态与地理环境监测国家测绘地理信息局重点实验室,江西吉安 343009)
基于Pareto支配的MPRM电路面积与可靠性优化
卜登立1,2,3,江建慧2
(1.井冈山大学电子与信息工程学院,江西吉安 343009; 2.同济大学软件学院,上海 201804; 3.流域生态与地理环境监测国家测绘地理信息局重点实验室,江西吉安 343009)
针对MPRM(Mixed-Polarity Reed-Muller)电路的面积与可靠性折中优化问题,在逻辑级建立面积估算模型以及电路SER(Soft Error Rate)解析评价模型,并采用Pareto支配概念对MPRM电路进行面积与可靠性多目标优化.通过对MPRM电路的XOR部分进行树形异或门分解,并考虑多个输出之间异或门的共享,建立面积估算模型.采用信号概率和故障传播方法,并考虑电路中的逻辑屏蔽因素以及信号相关性,建立电路SER解析评价模型.根据所提出的面积和SER评价模型,采用极性向量的格雷码序穷举搜索MPRM的极性空间得到MPRM电路面积与可靠性的Pareto最优解集,并使用效率因子技术指标选取最终解.MCNC基准电路的实验结果表明,与面积最小MPRM电路相比,所选取的MPRM电路可以在较小面积开销的前提下获得较高电路可靠性.
MPRM电路;可靠性优化;面积优化;SER解析评价模型;Pareto支配;多目标优化
1 引言
随着集成电路技术和工艺的发展,无论是传统的CMOS器件,还是纳米器件,其缺陷率均不可避免的增加,同时对瞬时故障(Transient Fault,TF)的敏感度也不断增加[1,2].因此,电路可靠性问题成为一个不容忽视的问题,需要在电路设计流程的各个阶段考虑可靠性约束.
RM(Reed-Muller)逻辑是布尔函数基于AND/XOR的逻辑表示[3],与基于AND/OR的逻辑表示相比,其电路实现具有面积和速度优势,因此在算术电路、校验电路和通信电路等领域得到了较为广泛的应用[4,5].近些年来,RM电路的逻辑综合以及优化得到了较多关注.如文献[3]进行MPRM (Mixed-Polarity RM)电路的逻辑优化,文献[4]进行FPRM(Fixed-Polarity RM)电路的面积优化,文献[5]进行混合极性RM电路的面积优化,文献[6]对包含无关项的FPRM电路进行面积与功耗优化,文献[7]对MPRM 电路进行面积与延时优化.尽管针对单固定故障和桥接故障模型,RM电路可以实现具有通用测试集的确定可测性设计[8],从而简化测试生成并提高测试速度,但可测性设计进行的是基于故障覆盖率的分析,考虑的是最坏情况,得到的是一个可靠性下限值.要准确分析电路的可靠性,需要采用概率分析方法.另外,RM电路之所以具有良好的可测性,正是由于异或门没有输入控制值,即不能通过某个输入的信号值支配其输出的逻辑信号值,因此发生在异或门输入端的故障以及传播至其输入端的故障总是能够传播至其输出,这也导致基于XOR电路的信号可靠度相对较低[9].因此更有必要在进行RM电路综合与优化时结合可靠性约束,从而在保持RM电路其他优势的同时,相对提高其信号可靠度.然而当前还缺乏这方面的研究工作.
为较好地实现RM电路面积与可靠性之间的折中,快速且相对准确的电路可靠性评价方法以及较为详尽的面积估算模型是非常必要的.另一方面,当前关于RM电路的面积与功耗、面积与延时等多目标优化问题往往采用聚合函数方法[6,7].聚合函数方法具有一定的局限性,只有在多个目标的Pareto前沿(front)是凸函数时,其得到的解才是Pareto最优解[10].因此,有必要研究适用于RM电路面积与可靠性多目标优化的方法,避免优化结果过于偏向某个目标.
本文根据建立的纳电子MPRM电路结构,先对电路中的XOR部分进行树形异或门分解,然后估算电路的面积;采用信号概率[11]和故障传播方法,并考虑电路中的逻辑屏蔽因素以及信号相关性,针对单瞬时故障在逻辑级建立工艺无关的MPRM电路软错误率(Soft Error Rate,SER)解析评价模型.根据所提出的面积估算模型以及SER解析评价模型,采用Pareto支配概念,使用基于格雷码序的穷举搜索方法进行面积与可靠性多目标优化,得到Pareto前沿,实现面积和可靠性的折中优化,并通过实验进行了验证.
2 MPRM逻辑表示和极性转换
对于一个n输入、m输出的多输出布尔函数,其极性值为g的MPRM可以表示为如式(1)所示的多项式形式[5].
(1)
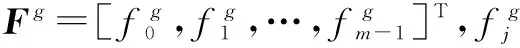
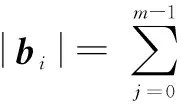
在MPRM电路优化过程中需要进行极性转换,OKFDD(Ordered Kronecker Functional Decision Diagram)[12]作为电路的判决图表示,也可用来实现极性转换.OKFDD使用非终端结点表示变量,1结点作为终端结点表示常量1,边表示函数.OKFDD通过依次对变量xl施香农分解和正、负Davio分解得到,三种分解类型分别对应gl=2、0和1.OKFDD中每个非终端结点有两个后继边,对这两个后继边进行XOR操作可以改变该结点所表示变量的分解类型[12],即改变该变量的极性.如果将OKFDD中由根结点到1结点的路径称为1路径,那么遍历OKFDD中的1路径即可得到其所包含的乘积项[12].
共享OKFDDs是在电路各个原始输出(Primary Output,PO)对应的OKFDD之间共享子图以降低空间复杂度.本文采用基于共享OKFDDs的极性转换方法[12]进行极性转换,先得到某个极性值的OKFDDs,然后由每个OKFDD得到其对应PO所包含的乘积项,再由m个PO所包含乘积项的并集得到如式(1)所示的MPRM表达式[12].由于MPRM表达式是由m个PO所包含乘积项的并集得到,因此可实现乘积项在多个PO之间的共享.
3 MPRM电路面积估算
根据式(1)可将MPRM电路分为由多输入与门构成的AND部分以及XOR部分.在RM电路可测性设计中,为缩短电路延迟,常将其中的XOR部分设计成树形2输入异或门结构[8],本文也采用这种结构,以便下一步的可测性设计实现.由于采用纳电子技术的双极器件[13]能够为逻辑门提供负极性的变量输入,因此本文结合纳电子技术建立如图1所示的纳电子MPRM电路结构,在此结构中多个PO之间可以共享异或门.

为进行面积优化,需要建立面积估算模型对电路面积进行评价.由图1可知AND部分的面积比较容易估算,而XOR部分面积估算的关键是确定其所包含2输入异或门的数量.
单输出电路的XOR部分共有t-1个异或门;但对于多输出电路,XOR部分异或门的数量取决于乘积项在多个PO之间的共享.因此,对于多输出电路,先对其XOR部分进行树形异或门分解,在不同PO的XOR部分分解过程中考虑异或门的共享,统计分解后电路中异或门的数量,然后再计算电路面积.
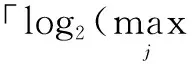

如果为单输出电路,如算法1中的Step2,可直接获得异或门数.如果为多输出电路,如算法1中的Step4,则需要调用如下所示的算法2依次对各个PO的XOR部分进行异或门分解.算法2中的|I|表示待分解宏门所包含的输入数量.

对于多输出电路,算法1依次对每个PO调用算法2进行XOR部分的分解,算法2在分解过程中通过XOR树查找实现异或门在各个PO之间的共享,因此算法1统计的是考虑异或门在多个PO之间共享后异或门的数量.
由算法1获得异或门的数量s后,根据式(2)计算MPRM电路的面积.
(2)
其中2×s为s个异或门的面积;wi为第i个乘积项所包含的文字数,也即该乘积项对应与门的面积,条件wi>1表明只有在乘积项中的文字数大于1时才存在对应与门.因为当wi=0时,表示常量1,此时可将驱动PO的异或门修改为同或门而不会改变电路的功能,当wi=1时,该文字直接作为异或门的输入,因此均不存在该乘积项对应的与门.
4 MPRM电路逻辑级可靠性分析
为分析瞬时故障对MPRM电路可靠性的影响,本文采用工艺无关的单瞬时故障模型[14,15],假设瞬时故障发生在逻辑门的输入端[15],并且区分0-TF和1-TF,0-TF指的是逻辑值由1变为0的故障,1-TF指的是由0变为1的故障.使用SER来评价电路的可靠性,SER指的是电路中节点发生的故障被传播至PO导致该电路出现软错误的比率.电路的SER值越小,其可靠性越高.
电路对瞬时故障存在多种屏蔽因素,由于本文进行工艺无关的电路优化,在逻辑级评价组合电路的SER,因此仅考虑逻辑屏蔽因素.
4.1 基于节点敏感度的电路SER计算

为简化分析过程,采用均匀故障模型,并假设节点发生0-TF和1-TF的概率相同,均为pf,则电路C的SER由式(3)计算.
(3)
与文献[2,15,16]不同,本文采用信号概率以及故障传播方法,分别计算节点故障被敏化的概率psens(ck),以及没有被后级电路逻辑屏蔽而传播至PO的概率pp(ck),然后根据式(4)计算pcrit(ck),并推导出SER与MPRM电路中异或门数以及与门扇入数间的解析关系.
pcrit(ck)=psens(ck)×pp(ck)
(4)
4.2 MPRM电路SER解析评价模型
下面先针对单输出电路进行分析,得到MPRM电路的SER解析评价模型,然后再分析其对多输出电路的适用性.
4.2.1 与门敏感度计算
与门的输入是原始输入(Primary Input,PI).假设所有PI相互独立,PI的信号概率为0.5,第i个与门的输入数为wi(wi>1).当与门的某个输入发生0-TF或1-TF时,其敏化概率为该输入的信号概率.对于单输出电路,与门的输出不存在扇出分支,并且异或门没有输入控制值,只要该故障能够传播至与门的输出,就可经XOR部分传播至PO,因而该故障的传播概率为其余wi-1个输入同时为1的概率:2-(wi-1).对于与门的一个输入端,如果既考虑0-TF又考虑1-TF,根据式(4)可知其敏感度为2-(wi-1).对于输入数为wi的与门,其敏感度由式(5)计算.
(5)
由于与门的各个输入信号相互独立,因此式(5)的计算结果是准确的.
4.2.2 异或门敏感度计算
尽管异或门的输入之间可能存在信号相关性,但对于单输出电路,异或门的输出也不存在扇出分支,因此如果其输入发生单故障,只要该故障被敏化,那么不管另一个输入信号为何值,该故障必然被传播至其输出,从而经后面的异或门传播至PO,可见故障的传播概率为1.由于异或门的输入由与门的输出或PI驱动,因此故障的敏化概率由驱动发生单故障输入的与门或PI确定,如果发生0-TF,需要该与门的输出或PI为1才能被敏化,即敏化0-TF的概率等于该与门的输出或PI为1的概率,设为psens0,同理,敏化1-TF的概率等于该与门的输出或PI为0的概率,设为psens1.因为总有psens0+psens1=1,因此根据式(4)可知异或门一个输入端的敏感度为1.异或门有2个输入端,因此异或门的敏感度为2.
由于考虑了信号相关性,因此异或门输入端故障传播概率和敏化概率的计算是准确的,异或门敏感度的计算也是准确的.
4.2.3 MPRM电路SER计算
尽管节点发生故障的概率pf与电路实现所采用的工艺有关,由于本文在优化过程中是进行不同极性值MPRM电路SER的比较,可以认为pf对不同极性值的MPRM电路而言均相同,因此在计算电路SER时不考虑pf.
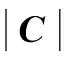
(6)
式(6)用于在极性优化过程中比较不同极性值MPRM电路的可靠性,SER值越小,可靠性越高.
对于多输出电路,尽管由于与门以及异或门在多个PO之间的共享,使与门和异或门的输出呈现扇出分支,但是不同的扇出分支属于不同的PO,并且只要有一个PO出现错误就认为该电路出现软错误,因此在计算电路SER时与门和异或门的扇出分支不会带来扇出重汇聚问题.另外,式(6)中的t为考虑乘积项在多个PO之间共享后的乘积项数量,s为考虑异或门在多个PO之间共享后的异或门数量,因此式(6)的SER计算不存在节点以及节点敏感度重复统计问题.可见式(6)同样适用于多输出电路,并且计算结果是准确的.
5 MPRM电路面积与可靠性优化
5.1 面积与可靠性多目标优化
由式(2)和式(6)可以看出面积与SER之间存在着冲突,因此MPRM电路的面积和可靠性优化问题属于多目标优化问题,并且由于面积与SER的Pareto前沿并不一定是凸函数,因此本文采用基于Pareto支配概念的多目标优化方法[10].
采用Pareto支配概念,MPRM电路面积与可靠性优化问题定义如下.
(1)由3n个决策变量向量G=[gn-1,gn-2,…,g0](gl∈{0,1,2})构成的极性空间为可行解空间;
(3)求Pareto最优解集:P={Gi|∃Gj∈F(Gj)F(Gi)},P⊆,对应的Pareto前沿:Q={F(Gi)|Gi∈P},Q⊆.
5.2 面积与可靠性优化算法
根据定义1所定义的多目标优化问题,本文采用穷举搜索极性向量空间的方法进行面积与可靠性优化.为加快搜索速度,按照极性向量的格雷码序(相邻的两个极性向量仅有一个极性属性编码值不同)进行搜索.使用外部归档来保存非支配最优解集,并在搜索过程中不断更新外部归档,最终得到Pareto最优解集以及Pareto前沿,并从Pareto最优解集中选取最符合实际需要的解.算法3给出了MPRM电路面积与可靠性优化算法的描述.

6 实验结果及分析
文中算法使用C++实现,并在Linux操作系统下使用g++编译器编译.使用算法3在配置为Intel Core i3-2350M CPU 6GB RAM的个人计算机上对24个MCNC电路进行了面积与可靠性优化,求得了Pareto最优解集以及Pareto前沿.
图2给出了电路5xp1、alu2以及t3的Pareto前沿,其中归一化面积是根据每个电路的Pareto前沿中的最小面积进行归一化处理的结果.
由图2可以看出,MPRM电路面积与可靠性的Pareto前沿并不是严格的凸函数,未给出电路的Pareto前沿也具有这个特点.这验证了使用Pareto支配进行MPRM电路面积与可靠性优化的必要性.

表1给出了对24个MCNC电路运行算法3的结果.其中“I/O”表示电路的输入数和输出数;“N-PF”表示Pareto最优解集的大小;“面积增加”和“SER减少”分别表示所选取的最优解相对于面积最小解所导致的面积开销和SER下降的比例.“所选取的最优解”是根据效率因子“E=SER减少/面积增加”所选取的最终解,其选取的原则是在E>1的前提下最大化E的值,如果不存在E>1的最优解,则选取面积最小解作为最终解,此原则的依据是尽可能在较小面积开销的前提下获得较大的可靠性提升.
由表1可以看出,这些电路的Pareto最优解集均包含多个非支配最优解,特别是cm151a,其非支配最优解数达到了134个.这验证了使用Pareto支配概念进行MPRM电路面积与可靠性优化的有效性.
根据效率因子E所选取的最终解中,有6个电路,最终解就是面积最小解,因为在这些电路的Pareto最优解集中,除面积最小解外的其他非支配最优解的E均小于1,也就是说尽管可以提高可靠性,但面积开销较大.对其余的18个电路,所选取最优解的E均大于1;除cm85a外,相对于面积最小的MPRM电路,最终所选取的MPRM电路均能够在较小面积开销的前提下获得较大可靠性提升;特别是clip和ex5,在不到1%的面积开销下,可靠性分别提升了6.10%和9.11%,其最终解的E分别为6.63和22.27.对表1中的这些电路,从平均角度看,所选取的最终解相对于面积最小解,面积增加了4.42%,SER减少了7.25%.
对于cm85a,尽管所选取最终解的效率因子达到了2.20,可靠性提升了33.09%,但面积开销达到了15.02%.表2给出了cm85a的MPRM电路面积与可靠性的Pareto前沿.
由表2可以看出,对于cm85a,除面积最小解外的5个非支配最优解均满足E>1,有较大的最终解选择空间.例如,可以选择面积开销为3.76%,SER减少5.21%的解.
另外,对表1中电路的最小面积解和最终解MPRM电路进行分析,在那些最终解不是最小面积的MPRM电路中,对于绝大多数电路而言,最终解的异或门数要小于最小面积解的异或门数,而与门的平均扇入数要略高于最小面积解的与门平均扇入数,这个结果符合式(6)的SER计算,因为异或门的敏感度较高,异或门的减少可以降低SER,与门扇入数的增加可以降低与门的敏感度.尽管可将此结果作为MPRM电路面积与可靠性优化的指导原则,但如果不附加其他原则,将会导致优化结果过于偏向可靠性目标.
对表1中21个多输出电路某个极性值的MPRM电路使用算法1计算了其所包含的异或门数,由于空间关系,这里仅给出统计结果.从平均角度看,有7个异或门被多个PO共享,占异或门总数的11.09%;与不考虑多个PO间的异或门共享相比,异或门数减少了13.45%;如果使用t来估算异或门数,异或门数被低估了23.15%.

表1 面积与可靠性多目标优化结果

表2 cm85a的Pareto前沿
综上所述,MPRM电路存在着较好的面积与可靠性折中空间,可以通过极性优化实现面积与可靠性之间的折中.较为准确的目标函数值估算以及采用Pareto支配概念进行多目标优化,能够更好地探索多个目标的折中空间,可以避免由于某个目标占绝对优势,使优化结果过于偏向这个目标.
7 总结与展望
对于一个布尔函数而言,存在着指数量级不同函数结构的MPRM,可以利用不同的MPRM函数结构来进行MPRM电路多个目标的折中优化.为了避免优化结果过于偏向某个目标,较为准确的目标估算以及恰当的优化策略对多目标优化而言至关重要.本文根据纳电子MPRM电路结构,给出了MPRM电路面积估算模型和SER解析评价模型,并使用Pareto支配概念进行了面积与可靠性优化,实验结果验证了所提出方法的有效性.通过合理地选择最终非支配最优解,可使MPRM电路在较小面积开销的前提下获得较大可靠性提升.
本文使用了穷举搜索进行MPRM电路的多目标优化,对于输入数较多的电路,穷举搜索无法在合理时间内获得Pareto最优解集.因此下一步的工作是研究用于MPRM电路多目标优化的基于Pareto支配的智能算法,提高多目标优化的时间效率.
[1]Rao W,Yang C,Karri R,et al.Toward future systems with nanoscale devices:overcoming the reliability challenge[J].Computer,2011,44(2):46-53.
[2]Luckenbill S,Lee J-Y,Hu Y,et al.RALF:reliability analysis for logic faults-an exact algorithm and its applications[A].Proceedings of the 2010 Design,Automation & Test in Europe Conference & Exhibition[C].IEEE,2010.783-788.
[3]Al-Jassani B A,Urquhart N,Almaini A E A.Manipulation and optimisation techniques for Boolean logic[J].IET Computers and Digital Techniques,2010,4(3):227-239.
[4]汪鹏君,李辉,吴文晋,等.量子遗传算法在多输出Reed-Muller逻辑电路最佳极性搜索中的应用[J].电子学报,2010,38(5):1058-1063.
Wang P J,Li H,Wu W J,et al.Application of quantum genetic algorithm in searching for best polarity of multi-output Reed-Muller logic circuits[J].Acta Electronica Sinica,2010,38(5):1058-1063.(in Chinese)
[5]卜登立,江建慧.基于对偶逻辑的混合极性RM电路极性转换和优化方法[J].电子学报,2015,43(1):79-85.
Bu D L,Jiang J H.Dual logic based polarity conversion and optimization of mixed polarity RM circuits[J].Acta Electronica Sinica,2015,43(1):79-85.(in Chinese)
[6]汪鹏君,汪迪生,蒋志迪,等.基于PSGA算法的ISFPRM电路面积与功耗优化[J].电子学报,2013,41(8):1542-1548.
Wang P J,Wang D S,Jiang Z D,et al.Area and power optimization of ISFPRM circuits based on PSGA algorithm[J].Acta Electronica Sinica,2013,41(8):1542-1548.(in Chinese)
[7]Jiang Z,Wang Z,Wang P.Delay-area trade-off for MPRM circuits based on hybrid discrete particle swarm optimization[J].Journal of Semiconductors,2013,34(6):132-137.
[8]Rahaman H,Das D K,Bhattacharya B B.Testable design of AND-EXOR logic networks with universal test sets[J].Computers and Electrical Engineering,2009,35(5):644-658.
[9]Limbrick D B,Yue S.Impact of synthesis constraints on error propagation probability of digital circuits[A].Proceedings of the 2011 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems[C].IEEE,2011.103-111.
[10]Chinchuluun A,Pardalos P M.A survey of recent developments in multiobjective optimization[J].Annual Operational Research,2007,154:29-50.
[11]Parker K P,Mccluskey E J.Probabilistic treatment of general combinational networks[J].IEEE Transactions on Computers,1975,C-24(6):668-670.
[12]Drechsler R,Becker B.Ordered Kronecker functional decision diagrams-a data structure for representation and manipulation of Boolean functions[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,1998,17(10):965-973.
[13]Ben-Jamaa M H,Mohanram K,De-Micheli G.An efficient gate library for ambipolar CNTFET logic[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2011,30(2):242-255.
[14]Krishnaswamy S,Plaza S M,Markov I L,et al.Signature-based SER analysis and design of logic circuits[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2009,28(1):74-86.
[15]Polian I,Hayes J P,Reddy S M,et al.Modeling and mitigating transient errors in logic circuits[J].IEEE Transactions on Dependable and Secure Computing,2011,8(4):537-547.
[16]Takata T,Matsunaga Y.A robust algorithm for pessimistic analysis of logic masking effects in combinational circuits[A].Proceedings of the 17th International on-Line Testing Symposium[C].IEEE,2011.246-251.

卜登立 男,1975年出生,河北定州人.博士,副教授.主要研究领域为VLSI设计和可靠性评估、计算机辅助设计.
E-mail:bodengli@163.com

江建慧 男,1964年出生,浙江淳安人.博士,教授,博士生导师,CCF高级会员.主要研究领域为可信系统与网络、软件可靠性工程、VLSI/SoC测试与容错.
E-mail:jhjiang@tongji.edu.cn
Pareto Dominance Based Area and Reliability Optimization of MPRM Circuits
BU Deng-li1,2,3,JIANG Jian-hui2
(1.SchoolofElectronicsandInformationEngineering,JinggangshanUniversity,Ji’an,Jiangxi343009,China;2.SchoolofSoftwareEngineering,TongjiUniversity,Shanghai201804,China;3.KeyLaboratoryofWatershedEcologyandGeographicalEnvironmentMonitoringNASG,Ji’an,Jiangxi343009,China)
Area and SER (Soft Error Rate) evaluation models at logic level are proposed for area and reliability optimization of MPRM (Mixed-Polarity Reed-Muller) circuits,the trade-off between area and reliability is achieved by using Pareto dominance based multiobjective optimization.The area is computed by decomposing the XOR part of MPRM circuit as trees of XOR gates and counting in XOR gate sharing among multiple outputs.The SER is computed by using signal probability and fault propagation techniques,and taking into account the logic masking effects and correlations among signals in the circuit network.Based on the proposed area and SER evaluation models,the Pareto optimal set for area and SER of MPRM circuit is obtained by using polarity optimization method with Gray code based exhaustive search strategy,the final solution is selected by using a metric called efficiency factor.Experimental results by using a set of benchmark circuits from MCNC show that,in comparison with the MPRM circuits with minimized area,the selected MPRM circuits have improved reliability with less area overhead.
MPRM circuits;reliability optimization;area optimization;analytical SER evaluation model;Pareto dominance;multiobjective optimization
2015-05-05;
2015-10-28;责任编辑:蓝红杰
国家自然科学基金(No.61432017);流域生态与地理环境监测国家测绘地理信息局重点实验室资助课题(No.WE2016012);吉安市科技局指导性科技计划(吉市科计字[2016]4-4)
TP331.2,TP391.72,TP202+.1
A
0372-2112 (2016)11-2653-07
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.11.013

