基于多点信息统计法的土地覆盖图像超分辨率重建方法
杜 奕,张 挺
(1.上海第二工业大学工学部,上海 201209;2.上海电力学院计算机科学与技术学院,上海 200090)
基于多点信息统计法的土地覆盖图像超分辨率重建方法
杜 奕1,张 挺2
(1.上海第二工业大学工学部,上海 201209;2.上海电力学院计算机科学与技术学院,上海 200090)
在利用遥感技术对土地覆盖情况制图的过程中,超分辨率重建被广泛采用.包含土地覆盖图像特征的先验模型可以减少重建过程中的不确定性.多点信息统计法可以从先验模型提取其本质特征,然后将特征复制到待模拟区域.然而传统基于线性降维的多点信息统计法不能有效处理非线性数据,因此将等距特征映射引入到多点信息统计法以实现非线性数据的降维,再对降维后的数据作分类处理.比较当前数据事件和各个分类的均值,从与当前数据事件最接近的类中提取模式.同时利用低精度原始图像作为软数据以重建较高精度的土地覆盖图像.实验表明重建的超分辨率土地覆盖图像具有与参照图像相似的结构特征.
土地覆盖;遥感;多点信息统计法;等距特征映射;超分辨率重建
1 引言
土地覆盖是指土地表面的生态状态和自然表现,它在描绘地球环境和生物变化以及人地交互系统中发挥着重要作用.遥感技术为获取土地覆盖信息提供了便利的工具.采用遥感技术可以从最新的遥感影像上识别出地表的土地覆盖现状,以便及时地获取区域乃至全球尺度的土地覆盖信息[1~3].为得到高分辨率的土地覆盖图像,可以改进现有的传感器制造技术,减小像素的尺寸,但是改进难度较大,并且在现有的传感器制造技术条件下,传感器的大小和密度已经接近极限,很难有较大突破.但是,人们可以相对容易地得到同一目标不同情况下的一幅或多幅图像,这些图像中包含了该目标的多种有用信息,如果能够将这些信息融合进入一幅图像就可以突破该图像的分辨率限制,提高目标的可辨识程度.这种分辨率增强方法通常称为超分辨率(Super Resolution,SR)重建技术[4~7].
超分辨率重建主要可以分为三类[7~12]:基于插值的方法,基于多幅图像的方法和基于事例学习的方法.基于事例学习的方法通过对训练图像的学习来提取其本质的模式特征,以重建高分辨率图像[11,12].作为随机模拟方法的一个重要分支,多点信息统计法(Multiple-Point Statistics,MPS)能够从训练图像中捕捉复杂的特征样式并把它们复制到待重建区域中,即通过再现训练图像的高阶统计量以重建最终结果[13,14].但在MPS重建数据过程中,虽然训练图像的模式特征决定模拟结果,但这些模式往往维数较高,数据处理较为困难.因此,模式降维问题成为MPS的研究热点.降维方法可以分为线性降维和非线性降维两类.一部分主流MPS算法,如过滤器随机模拟(Filter-Based Stochastic Simulation,FILTERSIM)[13],虽然将数据降维引入到其算法过程中,但是其采用线性降维方法处理所有数据,那么将会严重降低MPS重建的质量.因此应当引入非线性降维方法处理上述数据降维问题.
另外,条件数据对重建结果的影响很大.条件数据包含硬条件数据和软条件数据.在许多领域里,由于受到客观条件或技术水平限制,所能得到的硬条件数据非常有限,但是可以获得相对比较丰富的软条件数据.如果能充分利用较为丰富的软条件数据,那么必然会提高重建图像的精度.
本文提出一种利用MPS实现土地覆盖图像超分辨率重建的方法.为了解决训练图像非线性降维的问题,拟采用等距特征映射(Isometric Mapping,ISOMAP)实现训练图像的非线性降维[15].同时为了提高图像重建的精度,将低分辨率情况下的原始土地覆盖图像作为重建过程中的软数据.
2 算法的具体步骤
本文算法共分为四个步骤,各个步骤依次详述如下.
2.1 第一步:建立训练图像的模式库
2.1.1 数据模板和数据事件
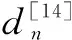
dn={S(uα)=skα;α=1,2,…,D;kα∈[1,K]}
(1)
上式表示D个向量在uα位置的S(u1),…,S(uD)分别为状态值sk1,…,skD.
2.1.2 建立模式库
利用数据模板扫描训练图像来捕获数据事件,这些数据事件又被称为“模式”.如果按照每次移动一个节点(即像素),从左到右,从上到下进行扫描,那么就可以获得训练图像全部的模式库.
设TI(u)表示以u为中心的模式,ti(u+hi)(i=1,2,…,D)表示u+hi位置的属性值,那么有:
TI(u)=(ti(u+h1),ti(u+h2),…,ti(u+hD))
(2)
可见模式TI(u)和数据模板尺寸相同.如果将各个模式从训练数据中抽取出来形成模式库,那么与具体位置u无关,此时可设模式库中的模式个数为Npat,那么第k个模式可以表示为:
patk=(patk(h1),patk(h2),…,patk(hD)),
k=1,2,…,Npat
(3)
其中patk(hi)与ti(u+hi)相对应.整个模式库patDb可以表示为:
patDb=(pat1,pat2,…,patNpat)
(4)
2.2 第二步:利用ISOMAP实现模式的降维
如前所述,本文利用ISOMAP实现模式的非线性降维.ISOMAP是流形学习中经常采用的一种非线性映射方法,它以多维尺度变换(Multi-Dimensional Scaling,MDS)为基础,利用所有样本点对之间的测地距离矩阵来代替MDS算法中的欧氏距离矩阵,以保持嵌入在高维观测空间中的内在低维流形的全局几何特性.
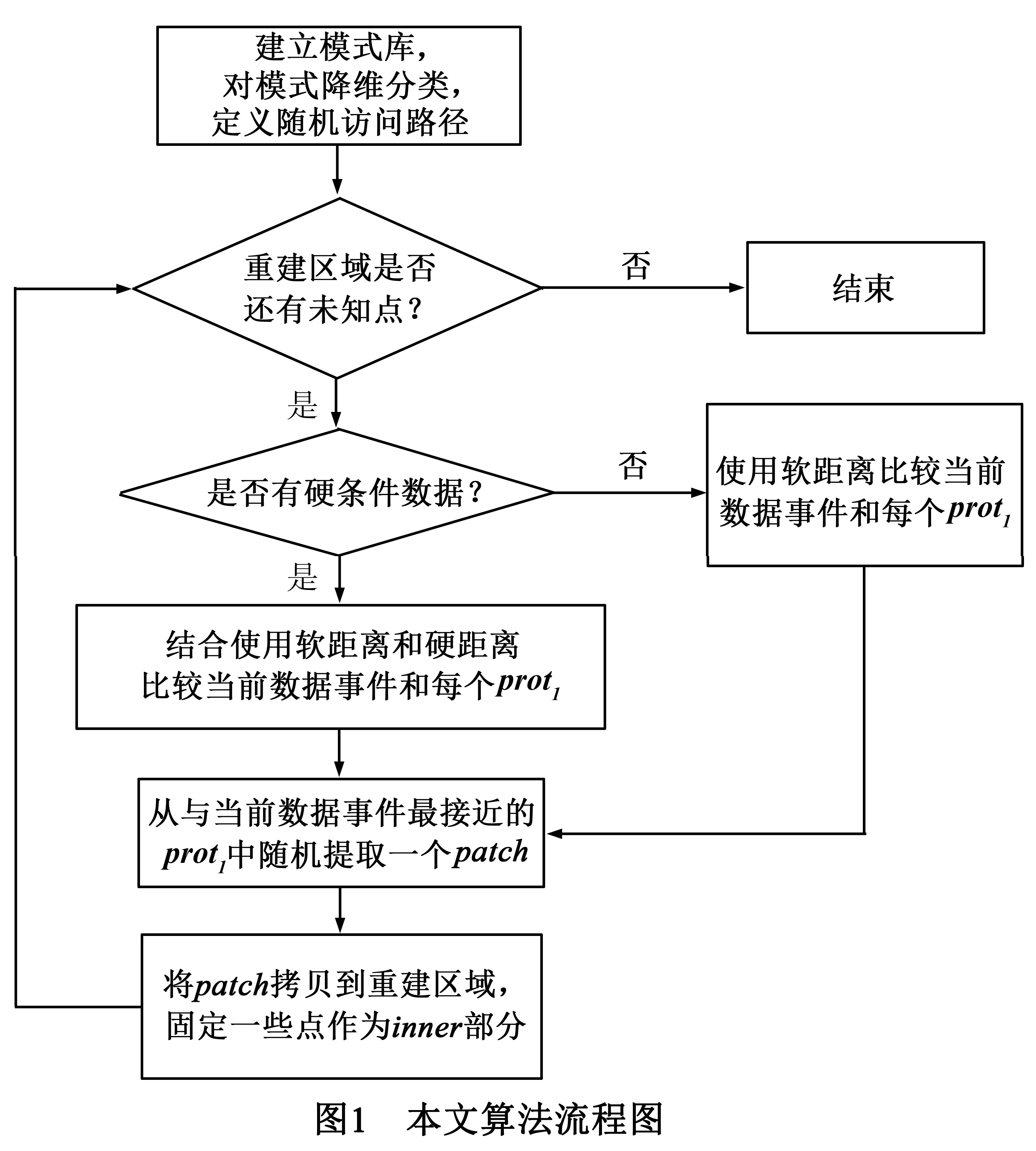
由于捕获的每个模式patk(k=1,2,…,Npat)含有D个分量,可以视其维数为D.降维过程是通过ISOMAP将patDb中的样本patk降维到d(d< ①构造模式近邻图G:计算模式库patDb中所有模式对(pati,patj)间的欧氏距离,记为dE(pati,patj): dE(pati,patj)= (5) 比较欧氏距离,确定每个模式的k个最相似模式;构造模式近邻图G,图G中的节点和各模式一一对应,边代表近邻关系,即如果pati和patj是相似模式,G中对应节点i和j用边连接,否则断开.边权值用模式间欧氏距离dE(pati,patj)表示. ②计算模式间的最短路径dM(pati,patj):当图G中存在边(i,j)时,设最短路径dM(pati,patj)=dE(pati,patj),否则dM(pati,patj)=∞,对于p=1,2,…,Npat: dM(pati,patj)=min{dM(pati,patj),dM(pati,patp) +dM(patp,patj)} (6) 设最短路径距离矩阵为DM=(dM(pati,patj))2,i,j=1,2,…,Npat,而公式(6)本质上可以视为在加权图中求取最短路径的Floyd算法,是一个递归求路径最小值的过程[16]. ③计算低维映射:计算对称阵 (7) 这里的I是Npat阶单位阵,l是元素全为1的Npat维列向量.低维空间的维度为d,则求取矩阵B的d个最大的特征值λ1≥λ2≥…≥λd,对应的特征向量是α1,α2,…,αd,则可得降维后的各个模式: (8) 2.3 第三步:模式的分类 在完成训练图像中模式的降维后,可采用聚类方法对获取的低维模式进行分类.本文选定k-means方法作为聚类方法.在利用k-means划分模式空间后,获得若干“子空间”,每个子空间命名为Cell.对于每个Cell,可以定义一个与数据模板相同形状的“平均模式”,称为Prototype.Prototype是属于该Cell的所有模式在原高维空间中各像素位置的均值. 令Prototype的值为prot(l)(hα),它表示属于一个Cell的所有模式在各个hα位置的均值,定义为: prot(l)(hα)= (9) protl= (prot(l)(h1),prot(l)(h2),…,prot(l)(hD)), l=1,…,L (10) 如果将一个Cell中的模式视为一类,上述protl即第l个模式类的平均模式特征. 2.4 第四步:模式的提取 在重建土地覆盖的超分辨率图像时,低分辨率的原始图像信息总是存在的,这些信息可以作为重建图像时的软条件数据.利用扫描训练图像时使用的数据模板扫描图像的待重建区域,检索以未知点u为中心的数据事件内的所有已知像素点,这些点视为硬条件数据.设已知硬条件数据点数目为n′(≤D).在重建的开始阶段,这些硬条件数据数量十分有限甚至n′=0,即无硬条件数据而只有软条件数据.随着重建过程的深入,越来越多像素点被模拟重建,硬条件数据数量开始增多,这些像素点成了其他后继像素点模拟的硬条件数据,此时变成了结合软硬条件数据情况下的重建. 当提取训练图像的模式(称为patch)时,这个patch本质上即训练图像内的图像块.将patch分为两个部分:inner部分和outer部分.它们可以作为其他后继像素点重建的硬条件数据.不同之处在于,inner部分会被“固定”为重建结果,不会再对其进行模拟;而patch的outer部分不仅作为其他像素点模拟的条件数据,而且该部分的所有像素点会被当作未知点重新模拟. 设t表示数据类型,则patch中一共可能有3种数据: (a)t=1:原始硬条件数据,它们被分配到各像素点位置上. (b)t=2:已经模拟过的像素点,它们被固定为硬条件数据,即patch的inner部分(不包含inner部分内的原始硬条件数据). (c)t=3:通过“粘贴”Prototype中的patch而已知的像素点,但这些点会被重新模拟,即patch的outer部分(不包含outer部分内的原始硬条件数据). 另外定义“距离函数”如下: dis(d(uα),protl)= t=1,2,3;l=1,…,L, (11) dis(d(uα),protl)表示求取数据事件d(uα)和protl中对应的已知像素点间的距离.每种像素点会根据其类型而给定一个权值ω(t),表示其在求取距离中的重要性,注意有ω(3)≤ω(2)≤ω(1).假设以u为中心的硬条件数据事件hd(u)与各个protl之间的距离可以表示为: (12) (13) 对于软条件数据(即低分辨率的原始图像),设软条件数据事件sd(u),同理可得第l个“软距离”: (14) 软条件数据的距离向量为: (15) 由上可得软硬条件数据情况下数据事件与protl之间的距离向量: Distotal=perhd×Dishd+μ×Dissd (16) 其中perhd表示在数据模板中已知硬条件数据的像素数占模板总像素数的百分比;而μ(0≤μ≤1)是表示软数据准确性的权值.Dishd和Dissd要进行归一化处理.在获取Distotal之后,从其各个分量中寻找最小值,假设该最小值对应序号为R,则从protR对应的Cell中随机提取出一个patch,然后将其复制到以当前模拟点u为中心的待重建区域.重复上述步骤直到所有点模拟完毕. 整个算法的完整流程归纳如下: ①利用数据模板扫描训练图像,构建模式库patDb. ②利用ISOMAP对模式库中的模式进行降维. ③采用聚类方法k-means对降维后的模式进行分类. ④定义一条随机访问路径,对重建区域内的未知点进行访问.检查当前路径上的待模拟像素点u是已知的硬条件数据(即t=1类型点)还是已模拟点(即t=2类型点).如果是已知的硬数据或已模拟点,则对随机路径上的下个像素点进行判定;否则转向步骤⑤; ⑤利用公式(16)寻找与当前数据事件最为接近的protl,从该protl对应的Cell中随机提取出一个patch,然后将patch粘贴到以当前像素点u为中心的待重建区域上. ⑥重复步骤④到⑤,继续对其他点进行模拟,直到随机路径上的所有像素点被模拟完毕. 算法流程图如图1所示. 4.1 土地覆盖图像重建实例 所有实验都是在Intel Core i5 2450MHz CPU和2GB DDR3内存环境下运行的.公式(11)中的权值ω(1)=0.5,ω(2)=0.3,ω(3)=0.2.公式(16)中的μ设定为μ=1-perhd.整个patch的尺寸为17×17像素,其inner部分设置为9×9像素.如图2所示,利用两幅实际获得的长江三角洲区域的土地覆盖图像作为参照图像,两幅图像分别称为Case #1和Case #2.每幅图包含512×512像素,空间分辨率为30m.可以看出Case #1包含了一些分散的森林,在图中央区域有一个湖泊;而Case #2有很多农田,一条河流贯穿整幅图.Case #1和Case #2都有少量的道路. 对上述参照图像的像素进行分块均值化处理,目的是生成对应的粗精度情况下的低分辨率图像,这些低分辨率图见图3和图4.图3是这样获得的:将图2(a)和图2(b)分成若干32×32像素大小的图像块,对每个图像块内的灰度值取均值.这样可以获得16×16个由粗精度像素块组成的低分辨率图.图4与图3同理,是对参照图像按照每8×8像素取其均值获得的,则可以得到64×64个由粗精度像素块组成的低分辨率图,显然图4精度较高. 选取两幅长江三角洲区域800×600像素的土地覆盖图像作为训练图像,分别如图5(a)和(b)所示,空间分辨率都是30米.尽管训练图像和参照图像并不相同,但它们均含有相似的模式,如湖泊、森林、农田、河流和道路.在超分辨率重建过程中,图3(a)和4(a)分别用作Case #1超分辨率重建时的粗粒度软数据,它们的训练图像是图5(a);而图3(b)和图4(b)分别用作Case #2超分辨率重建时的粗粒度软数据,它们的训练图像是图5(b).利用上述软数据重建的超分辨率图像如图6和图7所示.可以看出,利用较高分辨率的图4(a)和4(b)重建的图像质量较好. 4.2 重建质量评价 与获得图3的方法同理,对图6(a)按照每32×32像素取其均值获得低分辨率图像,可获得16×16个粗粒度的图像块,每个图像块的值即该图像块内32×32像素的灰度均值.以上述图6(a)粗粒度情况下的图像块各均值为横坐标,图3(a)相同位置图像块的灰度值为纵坐标,可以得到一张粗粒度图像块灰度值分布的散点图,如图8(a)所示.同理可以获得图6(c)与图3(b)的散点图(见图8(b)).如果散点分布在45°直线附近,说明重建图像和参照图像的粗粒度图像块的灰度值接近,重建质量较高.可以看出图8(a)和8(b)中散点在45°线附近分布得不够集中,说明重建后各图像块的均值波动较大.对于图7(a)和图4(a),图7(c)和图4(b)分别绘制类似的散点图(见图9(a)),图中散点分布较为集中,说明重建后图像块均值波动较小,这表明分辨率较高的低分辨率图作为软数据有利于提高图像重建质量. 在对土地覆盖图像进行超分辨率重建时,由于缺少更高分辨率的空间数据,会导致重建结果有较多的不确定性.引入先验信息将有助于减少重建结果的不确定性,因此本文利用MPS提取土地覆盖训练图像的结构特征作为先验信息,以提高重建质量. 传统MPS处理线性数据效果较好,但是并没有针对非线性数据提出具体的处理策略.本文采用ISOMAP对训练图像中的模式数据进行降维处理.ISOMAP作为一种非线性降维方法,适用于降低非线性数据的维度.在重建过程中,将低分辨率原始图像作为软数据参与图像重建.实验验证了方法的有效性,而且证明较高分辨率的软数据能有效提高图像重建质量. [1]骆成凤.中国土地覆盖分类与变化监测遥感研究[D].北京:中国科学院遥感应用研究所,2005. Luo Cheng-feng.Remote sensing study of land cover classification and change in China [D].Beijing:Institute of Remote Sensing Applications,Chinese Academy of Sciences,2005.(in Chinese) [2]Boucher A,Kyriakidis P C.Super-resolution land cover mapping with indicator geostatistics[J].Remote Sensing of Environment,2006,104(3):264-282. [3]Boucher A,Kyriakidis P C,Cronkite R C.Geostatistical solutions for super-resolution land cover mapping[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(1):272-283.[4]潘宗序,禹晶,肖创柏,等.基于自适应多字典学习的单幅图像超分辨率算法[J].电子学报,2015,43(2):209-216. Pan Zong-xu,Yu Jing,Xiao Chuang-bai,et al.Single image super resolution based on adaptive multi-dictionary learning[J].Acta Electronica Sinica,2015,43(2):209-216.(in Chinese) [5]Zhang K,Gao X,Tao D,et al.Single image super-resolution with multiscale similarity learning[J].IEEE Transactions on Neural Networks and Learning Systems,2013,24(10):1648-1659. [6]Kim K I,Kwon Y.Single-image super-resolution using sparse regression and natural image prior[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(6):1127-1133. [7]Li X,Orchard M T.New edge-directed interpolation[J].IEEE Transactions on Image Processing,2001,10(10):1521-1527. [8]Li M,Nguyen T.Markov random field model-based edge-directed image interpolation[J].IEEE Transactions on Image Processing,2008,17(7):1121-1128. [9]Kim S P,Su W Y.Recursive high-resolution reconstruction of blurred multiframe images[J].IEEE Transactions on Image Processing,1993,2(4):534-539. [10]Li X,Gao X,Hu Y,et al.A multi-frame image super-resolution method[J].Signal Processing,2010,90(2):405-414. [11]Freeman W T,Jones T R,Pasztor E C.Example based super resolution[J].IEEE Computer Graphics and Applications,2002,22(2):56-65. [12]Gao X,Zhang K,Li X.,et al.Joint learning for single-image super-resolution via a coupled constraint[J].IEEE Transactions on Image Processing,2012,21(2):469-480. [13]Zhang T F.Filter-based training pattern classification for spatial pattern simulation [D].Palo Alto:Stanford University,2006. [14]Honarkhah M.Stochastic simulation of patterns using distance-based pattern modeling [D].Palo Alto:Stanford University,2011. [15]Tenenbaum B J,Silva V,Langford C J.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(22):2319-2323. [16]Hougardy S.The Floyd-Warshall algorithm on graphs with negative cycles[J].Information Processing Letters,2010,110:279-281. 杜 奕 女,1977年7月出生,江苏吴江人.2007年获得中国科学技术大学博士学位,现为上海第二工业大学工学部副教授,主要研究方向为数据挖掘和图像重建. E-mail:duyi@sspu.edu.cn 张 挺(通讯作者) 男,1979年9月出生,安徽安庆人.2009年获得中国科学技术大学博士学位,现为上海电力学院计算机科学与技术学院副教授,主要研究方向为图像重建. E-mail:tingzh@shiep.edu.cn A Super-Resolution Reconstruction Method for Land Cover Maps Using Multiple-Point Statistics DU Yi1,ZHANG Ting2 (1.CollegeofEngineering,ShanghaiSecondPolytechnicUniversity,Shanghai201209,China; 2.CollegeofComputerScienceandTechnology,ShanghaiUniversityofElectricPower,Shanghai200090,China) When using remote sensing for land cover mapping,super-resolution reconstruction is widely used.Prior models containing the features of land cover maps can constrain the uncertainty of reconstruction.These prior models can be used properly by multiple-point statistics (MPS) by extracting the intrinsic features from them,and copying these features to the simulated regions.However,because traditional MPS methods based on linear dimensionality reduction are not suitable to deal with nonlinear data,isometric mapping (ISOMAP) is introduced in MPS to reduce the dimensionality reduction of nonlinear data and then these lower-dimensional data are classified.Current data event and the average of every classified class are compared so that a pattern can be extracted from the class that is closest to the current data event.Besides,the low-resolution original image is viewed as soft data for generating super-resolution land cover maps.Tests show that the super-resolution reconstructions of land cover maps have the similar structural features with those of reference images. land cover;remote sensing;multiple-point statistics;isometric mapping;super-resolution reconstruction 2015-04-30; 2016-01-04;责任编辑:马兰英 中国科学院战略性先导科技专项 (No.XDB10030402);国家自然科学基金(No.41672114);上海第二工业大学校级重点学科建设软件服务工程项目(No.XXKZD1301);中石油与中科院重大战略合作项目(No.2015A-4812);上海市自然科学基金(No.16ZR1413200);上海第二工业大学校级重点学科建设计算机科学与技术项目(No.XXKZD1604) TP751 A 0372-2112 (2016)11-2576-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.11.003

3 算法的整体流程
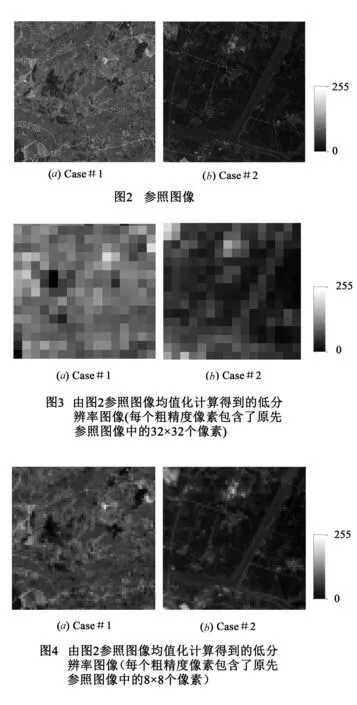
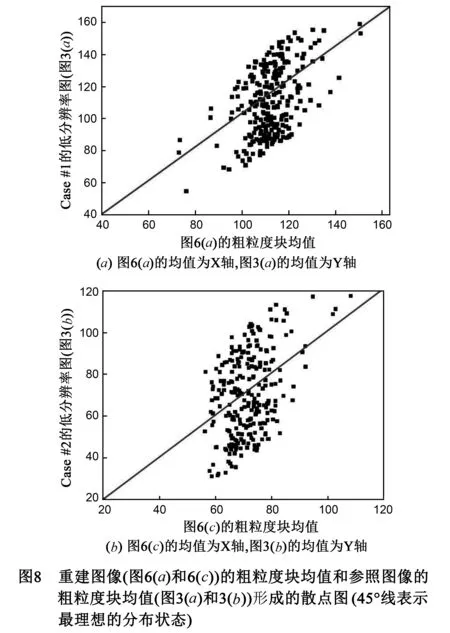
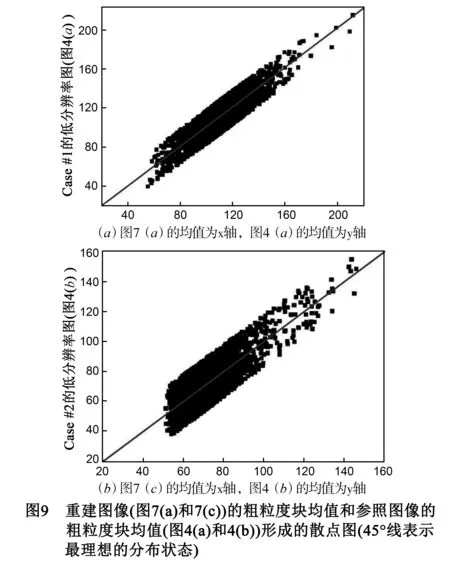
4 实验结果与分析



5 总结



