一种基于Stein无偏风险估计的复合去噪算法*
杨平先,黄坤超,周 兵
(1.四川理工学院自动化与电子信息学院,四川自贡643000;2.中国西南电子技术研究所,成都610036)
一种基于Stein无偏风险估计的复合去噪算法*
杨平先**1,黄坤超2,周 兵2
(1.四川理工学院自动化与电子信息学院,四川自贡643000;2.中国西南电子技术研究所,成都610036)
针对统计非局部均值滤波损坏图像的细节与鲁棒性双边带滤波去噪不充分的缺点,提出了一种基于统计非局部均值滤波与鲁棒性双边带滤波相结合的复合滤波算法。该复合滤波算法通过统计非局部均值滤波与鲁棒性双边带滤波线性组合,利用Stein无偏风险估计对复合算法中的参数进行估计。实验中,从主观与客观方面进行对比分析,证明所提出的复合算法体现了非局部均值滤波与双边带滤波的优点,能有效地去除噪声并更好地保留图像的细节信息,峰值信噪比提高1~2 dB。
图像去噪;非局部均值;双边带滤波;Stein无偏风险估计
双边带滤波针对高斯低通滤波只考虑了像素间的空域信息,未考虑图像灰度值的相似性。在高斯低通滤波只有空域高斯核函数的基础上,引入一个基于灰度值相似性的值域核函数,在卷积的过程中组合空域函数和值域核函数来实现的边缘保持去噪。双边带滤波同时考虑空域信息和灰度相似性,更好地实现图像去噪。但是,双边带滤波采用了基于灰度值的值域核函数,离边缘较远的像素基本上不会影响边缘的像素值,在对边缘像素值较好保持而不能有效地滤除边缘区域的高频噪声[8],且会将平滑区域的噪声当成边界而加强而形成伪边缘[9]。为了更充分滤除噪声,文献[10]在双边滤波前进行均值滤波,再通过均值滤波后的图像确定滤波核函数的一种鲁棒性双边滤波(Robust Bilateral Filter, RBF),以消除平滑区域伪边缘。
统计非局部均值滤波能有效地去除图像平滑区域的信息,但造成图像边缘区域的模糊。鲁棒性双边滤波增强了图像的边缘,但不能有效去除图像边缘区域的信息。本文针对统计非局部均值滤波与鲁棒性双边滤波的优缺点,将两者进行线性组合成一种复合滤波,并利用 Stein无偏风险估计[11-12](Stein′s Unbiased Risk Estimate,SURE)对复合滤波的参数进行估计,得到最优的参数。实验从主客观方面证明本文的复合滤波兼顾两者的优点,具有更好的去噪性能。
2 非局部均值与双边带复合去噪算法
2.1 统计非局部均值滤波
二维原始图像为f0={f0(i)|i∈I},给定一幅定义在有界域I⊂N2的图像受方差为σ2高斯白噪声n={n(i)|i∈I}的干扰,干扰后得到图像为f= {f(i)|i∈I},则可得到如下关系式:
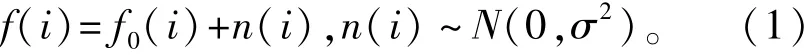
非局部均值利用像素附近相似性高、像素附近外区域相似度低的特点,将搜索区域Sl(通常取21× 21)噪声图像的像素进行加权平均来得到原始图像(该点的估计值f(i),表达式如下:
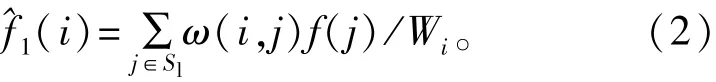
式中:Wi为归一化常数,定义为Wi=j∑∈Sω(i,j); l ω(i,j)为权值函数,其大小体现像素i、j为中心的两个区域的相似性,区域用P表示,通常取值为7×7或9×9,权值通过高斯加权欧氏距离获得:
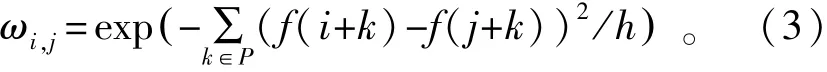
非局部均值充分去除了噪声,但造成图像边缘的模糊。于是出现了许多改进算法:文献[7]针对上式的权值未考虑噪声的影响,图像在受到高斯噪声干扰的情况下,将噪声的统计特性考虑进去并对权值系数进行修改,提出了基于噪声统计特性的统计非局部均值滤波(SPNLM)。该算法通过建立高斯噪声干扰的图像块的概率分布函数,由概率分布函数确定非局部均值的权值函数,有效地减小高斯噪声对权值的影响。SPNLM相对于传统NLM算法有效地去除了噪声,去噪后图像更好地接近原图,但仍然不可避免地造成图像边缘的模糊。
2.2 双边滤波
常用的图像滤波主要考虑了像素间的空间距离关系,但是却并没有考虑像素值之间的相似程度,因此去噪效果并不较好。双边滤波不仅考虑像素在空间距离上的关系,同时加入了像素间的相似程度,在去噪的同时能很好地保持边缘。双边滤波是由两个核函数构成一种保边去噪的滤波器,一个滤波核函数由图像几何空间距离决定,另一个滤波核函数由图像像素差值决定的。双边滤波表达式为
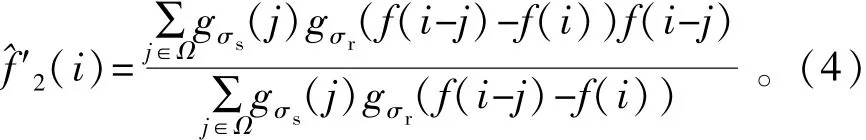
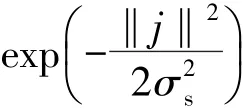

式中:f(i)是均值滤波后的结果。
2.3 复合去噪算法
非局部均值滤波未考虑到图像的几何信息,在充分滤除噪声的同时损坏了图像的边缘细节信息。双边带滤波同时考虑到图像的像素与空间信息,能较好保留图像的细节,但去除噪声不够充分。针对非局部均值与双边带滤波各自的特点,将非局部均值与双边带滤波线性组合构建一种复合滤波器模型,表达式如下:
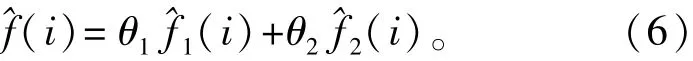
式中:^f1(i)为基于统计特性非局部均值的结果; ^f2(i)为鲁棒性双边滤波结果;^f(i)为复合去噪后的图像;参数θ1与θ2选取将决定去噪后的性能。对于参数的确定可以采用Stein无偏风险估计来确定,以实现最佳去噪。Stein无偏风险估计是在均方误差最小的前提下对原始图像的最优估计[13-15],当图像受到均值为0、方差为 σ2高斯噪声的影响时, SURE可以表示为
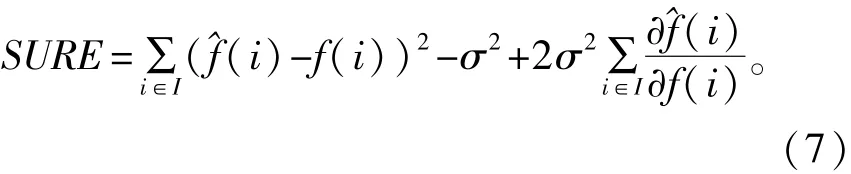
当SURE达到最小的时候,根据式(7)的凸性,其微分项将接近为0,再将式(6)代入式(7),可以得到
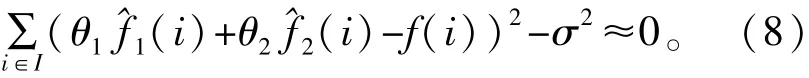
式(8)可以通过矩阵表示为Aθ=b,其中:
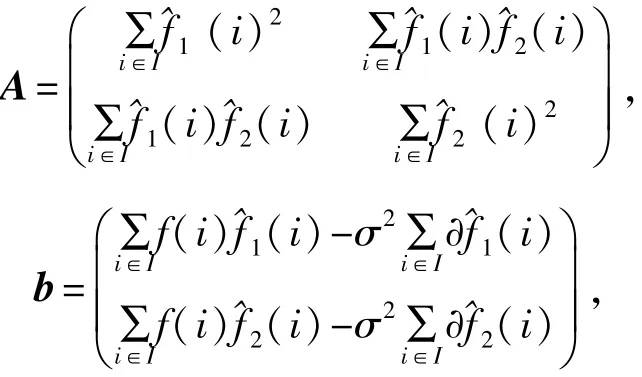
θ=(θ1,θ2)。θ可以通过矩阵的相除而得到:

将求得的θ代入式(6)便可以得到SURE估计的图像。
4 试验结果及分析
为证明本文的复合去噪算法通过SURE估计得到的参数θ1与θ2的合理性,将本文组合统计非局部均值与鲁棒性双边带滤波的复合滤波算法与固定参数θ1和θ2的复合滤波算法(θ1=θ2=0.5)、SPNLM滤波[7]、RBF滤波[10]进行对比分析。非局部均值滤波中涉及到的搜索区域与相似区域分别为Sl=21×21、P=7×7,双边带滤波器滤波空间区域Ω=5×5,复合滤波算法所需要的噪声方差采用文献[15]估计算法求得。实验采用的为HP Pavilion 15笔记本,其CPU为 i7,DDR3 4 GB。在客观评价方面选取了不同图片受不同强度高斯噪声干噪算法去噪后的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、结构相似度(Structural Similarity,SSIM)与去噪作为评价依据,列出部分代表性实验数据,如表1~4所示。表1~3给出了不同图片受不同强度高斯噪声干扰后采用不同去噪算法去噪后的PSNR、SSIM与去噪所用的时间,表4给出的是表1~3中的图片采用复合滤波算法去噪时使用的参数θ1与θ2的值。

表1 不同图片含不同强度的高斯噪声采用不同算法消噪后的PSNR比较Table 1 Comparison of output PSNR for differentalgorithms on different images corrupted by additive Gaussian noise with different variance
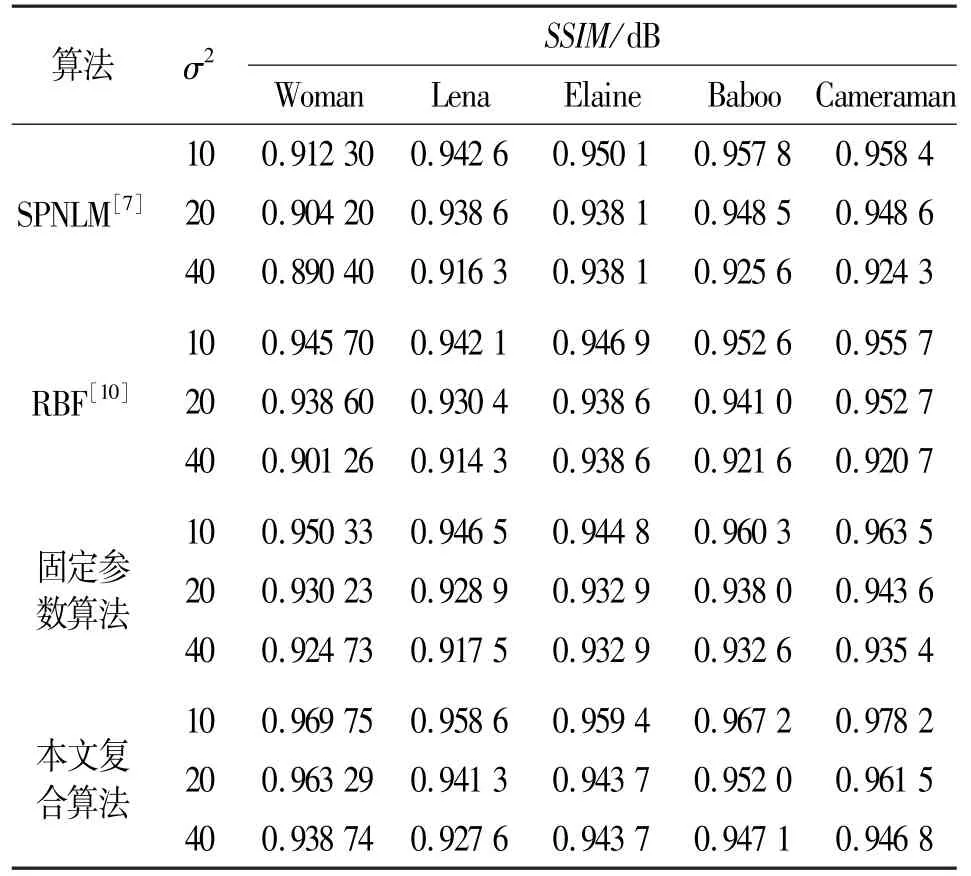
表2 不同图片含不同强度的高斯噪声采用不同算法消噪后的SSIM比较Tab.2 Comparison of output SSIM for different algorithms on different images corrupted by additive Gaussian noise with different variance

表3 不同图片含不同强度的高斯噪声采用不同算法消噪后的运算时间比较Tab.3 Comparison of output running time for different algorithms on different images corrupted by additive Gaussian noise with different variance

表4 复合算法对含不同方差的高斯噪声图片去噪时参数θ1、θ2的值Tab.4 θ1and θ2of the hybrid algorithm for different images corrupted by additive Gaussian noise with different variance
在主观评价方面,采用不同图像分别采用PNLM、RBF、固定参数复合算法以及本文的复合算法进行对比分析。图1给出了“Cameraman”图像不同算法去噪结果。从图中可以看出,PNLM算法能很好地去除平滑区域的噪声,在去除边界区域的噪声的同时在边缘区域产生离子效果形成人为的破坏;RBF能很好地保留图像的细节且增强了边缘,但不能有效地去除图像平滑区域的噪声;固定参数的复合算法是PNLM算法与RBF算法的折衷。采用SURE估计的复合算法得到最优参数,其去噪性能综合了PNLM算法与RBF算法的优点,细节的保持与噪声的消除都有较大的提高,不仅平滑区域去噪充分,且远处建筑的细节信息能较好地保留。
图2给出了表4中“Woman”“Lena”“Elaine”“Baboo”图像采用本文复合算法去噪结果以及复合算法采用的参数θ1、θ2的值。从图中可以看出,本文复合算法充分去除了平滑区域的噪声,且细节部分较好地保持。其中,θ1=0.783 1,θ2=0.227 5。
从表1~3中可以看出,固定参数的复合模型算法的PSNR、SSIM值有时高于SPNLM、RBF的PSNR、SSIM,有时低于SPNLM、RBF的PSNR、SSIM,未能综合SPNLM与RBF算法的优点;而本文的复合滤波算法的PSNR与SSIM值在各种算法中都最大。由此可知,本文的复合算法采用SURE估计得到合理的参数θ1与θ2,综合了非局部均值与双边带滤波的优点,性能远优于固定参数θ1与θ2的复合滤波算法,相对SPNLM与RBF其PSNR提高1~2 dB,去噪性能最优。
在运算耗时方面,SPNLM相对于RBF耗时较大,固定参数复合算法运算时间近似为SPNLM与RBF的运算时间之和,本文复合算法运算时间略大于固定参数复合算法运算时间,主要原因是本文复合算法在固定参数复合算法基础上增加了噪声方差的估计与θ1、θ2的求解。本文复合算法耗时最长,但相对固定参数复合算法增加的时间量小于0.25 s,增加的相对耗时并不长。

图1 不同算法对Cameraman图像消噪结果Fig.1 Cameraman image denoised by different algorithms

图2 本文复合算法对不同图片图像消噪结果Fig.2 Different images denoised by the proposed hybrid algorithm
5 结 论
本文针对PNLM算法去噪的同时破坏图像的细节信息与RBF算法不能有效去除图像的噪声缺点,构建了复合PNLM算法与RBF算法的去噪算法,通过SURE估计的复合算法的最优参数,使复合算法同时具有PNLM算法去噪充分与RBF算法保持图像细节的优点。试验中与PNLM算法、RBF算法以及固定参数的复合算法进行对比分析比较,实验结果从主客观证明了采用SURE估计的复合去噪算法能充分去除噪声,更好地保持图像的细节,峰值信噪比有所提高。在运算耗时方面,相对于固定参数的复合模型,本文复合去噪算法的参数的确定通过估计的噪声方差与图像的梯度进行矩阵运算而得到,从而增加了运算的时间,但是通过实验可知增加的运算时间量小于0.25 s,与PNLM和RBF算法耗时相比,本文复合算法增加的相对耗时并不长。因此,本文的复合去噪算法具有很好的应用前景。
[1] BUADES A,Coll B,MOREL J M.A non-local algorithm for image denoising[C]//Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Diego,CA,USA:IEEE,2005:60-65.
[2] ZHU S,ZENG B,LIU G,et al.Image interpolation based on non-local geometric similarities[C]//Proceedings of 2015 IEEE International Conference on Multimedia and Expo.Seattle,USA:IEEE,2015:1-6.
[3] LIU N,CHEN X.Infrared image detail enhancement approach based on improved joint bilateral filter[J].Infrared Physics&Technology,2016,77(9):405-413.
[4] KISHAN H,SEELAMANTULA C S.Sure-fast bilateral filters[C]//Proceedings of 2012 IEEE International Conference on Acoustics.Kyoto,Japan:IEEE,2012:1129-1132.
[5] HU J,ZHOU J,WU X.Non-local MRI denoising using random sampling[J].Magnetic Resonance Imaging, 2016,34(7):990-999.
[6] VIllE D V,KOCHER M.SURE-based non-local means[J]. IEEE Signal Processing Letter,2011,16(11):973-976.
[7] 陈明举.基于统计特性的非局部均值去噪算法[J].液晶与显示,2014,29(3):450-454. CHEN Mingju.Non-local means image denoising algorithm based on statisticalproperty[J].Chinese Journal of Liquid Crystals and Displays,2014,29(3):450-454.(in Chinese)
[8] GHOSH S,CHAUDHURY K N.On fast bilateral filtering using Fourier kernels[J].IEEE Signal Processing Letters,2016,23(5):570-573.
[9] CHAUDHURY K N,DABHADE S D.Fast and provably accurate bilateral filtering[J].IEEE Transactions on Image Processing,2016,25(6):2519-2528.
[10] CHAUDHURY K N,RITHWIK K.Image denoising using optimally weighted bilateral filters:a sure and fast approach[C]//Proceedings of 2015 IEEE International Conference on Image Processing.Quebec,Canada: IEEE,2015:108-112.
[11] QIU T,WANGA,YU N,et al.LLSURE:local linear SURE-based edge-preserving image filtering[J].IEEE Transactions on Image Processing,2013,22(1):80-90.
[12] KAVITHA P,VIJENDRAN A S.A novel edge preserving local linear stein's unbiased risk surface estimator approach for high dynamic range image[J].Indian Journal of Science&Technology,2016,9(6):1563-1572.
[13] XIE X C,KOU S C,LAWWRENCEA D.SURE estimates for a heteroscedastic hierarchical model[J].Journal of the American Statistical Association,2012,107 (500):1465-1479.
[14] CHEN G,ZHU F,HENG P A.An efficient statistical method for image noise level estimation[C]//Proceedings of 2015 IEEE International Conference on Computer Vision.Santiago,Chile:IEEE,2015:477-485.
[15] RANGACHARI S,LOIZOU P C.A noise-estimation algorithm for highly non-stationary environments[J]. Speech Communication,2006,48(2):220-231.

杨平先(1961—),男,四川自贡人,1990年于重庆大学获硕士学位,现为教授,主要研究方向为信息处理;
YANGPingxianwasborninZigong, Sichuan Province,in 1961.He received the M. S.degree from Chongqing University in 1990. He is now a professor.His research concerns information processing.
Email:ypingx@163.com
黄坤超(1971—),男,四川仁寿人,硕士,研究员,主要研究方向为测量技术与仪器;
HUANG Kunchao was born in Renshou,Sichuan Province, in 1971.He is now a senior engineer of professor with the M.S. degree.His research concerns measurement technology and instrument.
Email:kunchaoh402@126.com
周 兵(1978—),男,四川遂宁人,工程师,主要研究方向为信息管理与测试技术。
ZHOU Bing was born in Suining,Sichuan Province,in 1978.He is now an engineer.His research concerns information management and test technology.
A Hybrid Image Denoising Algorithm Based on Stein′s Unbiased Risk Estimation
YANG Pingxian1,HUANG Kunchao2,ZHOU Bing2
(1.College of Information Engineering,Sichuan University of Science&Engineering,Zigong 643000,China;
2.Southwest China Institute of Electronic Technology,Chengdu 610036,China)
For the problems that the statistical property non-local means(SPNLM)destroys the image′s detail and the robust bilateral filter(RBF)can not denoise effectively,a new hybrid algorithm based on SPNLM and RBF is presented.By calculating a linear combination of SPNLM and RBF,the new algorithm uses Stein′s unbiased risk(SURE)to estimate the optimal parameter.The new hybrid algorithm is comparatively analyzed from the subjective and objective aspects.Experimental results indicate that the new hybrid algorithm takes the advantages of SPNLM and RBF,removes the noise more effectively and preserves more image details,and the peak signal-to-noise ratio(PSNR)of denoising image is increased 1~2 dB.
image denoising;non-local means(NLM);bilateral filter;Stein′s unbiased risk estimation
1 引 言
非局部均值[1-2](Non-Local Means,NLM)与双边带滤波[3-4](Bilateral Filter,BF)是近几年兴起图像去噪技术。非局部均值去噪的思想是图像受干扰点的像素值可以通过图像其他区域相似块加权平均而得到,其去噪性能远好于传统均值滤波。但非局部均值仍存在不足:由于非局部均值利用图像中相似结构去除噪声,适用于空间结构性较强、冗余度较高的图像,且对图像的细节破坏严重[5-6]。近几年陆续出现了一些非局部均值滤波的改进算法,如:文献[7]提出了一种权值由相似块的统计特性确定的统计非局部均值滤波(Statistical Property Non-Local Means,SPN-LM),利用高斯噪声干扰的图像相似块的概率分布函数来确定权值大小,有效地减小高斯噪声对加权系数的不利影响,从而较好地提高了去噪性能。
The Project of Education Department of Sichuan Province(14ZB0211;14ZA0202);The Open Fund of Artificial Intelligence
**通信作者:ypingx@163.com ypingx@163.com
TN911.73
A
1001-893X(2016)11-1208-05
10.3969/j.issn.1001-893x.2016.11.005
2016-07-22;
2016-10-25
date:2016-07-22;Revised date:2016-10-25
四川省教育厅项目(14ZB0211;14ZA0202);人工智能四川省重点实验室开放基金项目(2015RZY01)
Key Laboratory of Sichuan Province(2015RZY01)
引用格式:杨平先,黄坤超,周兵.一种基于Stein无偏风险估计的复合去噪算法[J].电讯技术,2016,56(11):1208-1212.[YANG Pingxian, HUANG Kunchao,ZHOU Bing.A hybrid image denoising algorithm based on Stein′s unbiased risk estimation[J].Telecommunication Engineering,2016,56(11):1208-1212.]

