通信卫星星座优化设计综述*

莫 宇,闫大伟,游 鹏,雍少为

(国防科学技术大学电子科学与工程学院,长沙410073)

通信卫星星座优化设计综述*

莫 宇,闫大伟,游 鹏**,雍少为

(国防科学技术大学电子科学与工程学院,长沙410073)

通信卫星星座优化设计是构建通信星座系统的关键环节。对通信卫星星座设计中的优化模型和优化算法进行了综述和展望。首先,建立了通信卫星星座设计的一般优化模型;然后,从覆盖性能、星间链路和系统成本三个方面对优化模型中优化变量、目标函数和约束条件的构建进行了综述;之后,介绍了卫星星座设计中常用的三大类多目标优化算法,归纳总结了4种主流算法的主要特征,并比较分析了它们应用于卫星星座设计的优缺点;最后,指出了现有通信卫星星座优化设计中存在的问题及发展趋势。

卫星通信;星座设计;星间链路;多目标优化;优化算法

求解多目标多约束的优化问题,传统的优化方法不能有效解决,通常采用现代优化算法(遗传算法、粒子群算法等)进行星座设计,从而有效解决设计参数离散连续混合、目标函数非线性等问题,可以实现非均匀不对称星座设计,扩展了星座设计的解空间。应用该方法能获得满足多种约束条件下任务目标最优的星座设计方案,因此得到了广泛的研究和应用[2]。

目前,关于星座设计具体细节的研究较多,但对星座设计总结性的文献较少。本文针对多目标多约束的通信卫星星座设计问题,首先,建立通信卫星星座优化模型;然后,介绍现有的多目标优化算法及其在卫星星座设计中的应用,并指出星座设计现有研究中的不足;最后,总结全文,指出通信卫星星座设计的发展方向。

2 通信卫星星座优化模型

通信卫星星座设计是一个多目标多约束的优化问题。多目标优化问题的本质在于,各个子目标之间可能是相互冲突的。在通信卫星星座设计中,满足任务覆盖要求是前提。星座的覆盖范围受到轨道高度和仰角的影响,轨道高度越高覆盖范围越大,实现任务覆盖要求所需的卫星数目越少,系统成本越低,但随着轨道高度的增加,星间距离随之增大,建立星间链路所需的通信设备功率将提高,建立星间链路的难度也将增大。因此,覆盖性能、星间链路、系统成本等方面的目标具有一定的冲突,建立满足任务要求的多目标优化模型是通信星座设计的关键。

通信卫星星座设计可以建模为如下的数学模型:

式中:x为设计变量;fi(x)为目标函数;gi(x)为等式约束条件;hj(x)为不等式约束条件;p为目标函数个数;m和n分别为等式和不等式约束条件个数。

以上为通信卫星星座设计的一般优化模型。根据此模型,并结合通信星座的实际问题,本节将主要介绍通信卫星星座优化模型的建立过程。

2.1 覆盖性能

对于任何类型星座,覆盖性能指标皆是重要指标。卫星覆盖范围由卫星轨道高度和仰角共同决定。通信星座的覆盖一般有以下几种形式:根据时间分辨率的不同可以将覆盖分为连续覆盖和间断覆盖;根据覆盖范围的不同可以将覆盖分为全球覆盖和区域覆盖;根据覆盖重数的不同可以将覆盖分为单重覆盖和多重覆盖。在现有的星座设计研究中,根据任务的不同将覆盖性能建模为目标函数,如:最大化单重覆盖百分比[3]、最大化目标区域覆盖重数[4]等;或建模为约束条件,如:一天内需满足的重访次数[5]、至少满足区域单重连续覆盖[6]等;此外,也可将其同时建模为设计目标函数和约束条件,如在满足全球单重覆盖基础上最大化目标区域覆盖重数。

卫星与地面用户进行通信时,会受到多径效应和阴影效应的影响[7],因此,卫星与用户直接可见并不能保证良好的通信性能,通常需要判断卫星对用户是否为有效覆盖。实现有效覆盖可以采用增大仰角或多重覆盖的方法,越大的仰角越有利于减少多径衰落效应和遮蔽效应的影响,提高星座通信服务质量,如:仰角达到22.7°即可保证卫星通信系统95%以上的接通率[7];同样,多重覆盖能有效避免遮蔽问题,保证用户随时可与卫星通信。但仰角的增大会导致单颗卫星有效覆盖范围的减小,从而在同样覆盖要求下会增加卫星数目;覆盖重数的增多也会增加卫星数目,这都将导致系统成本的增加。

要准确建立卫星系统的覆盖模型,并将覆盖指标建模为目标或约束进行优化设计,需要对覆盖性能指标进行计算,星座设计过程中计算星座覆盖性能最常用的方法是网格法。网格法是以Rider[8]为代表提出的,该方法适用于分析任意类型轨道和任意复杂传感器的覆盖形状,同时对复杂应用环境具有较高的精度。这种方法的主要思想是以一定经纬度间隔作网格图,落在服务区内的网格点作为特征点,根据不同覆盖性能指标进行综合统计分析。

随着计算机技术的发展和复杂卫星系统覆盖性能求解的需求,网格法越来越受到人们的重视,因其精度高、适用范围广、通用性强等特点,已经成为航天工程界求解覆盖特性最主要的方法。

但是网格法同样也存在不足,随着地球纬度的升高,不同纬度圈上相同经度差的两点距离会越来越近,因此,等经度分割会使得特征点的分布随纬度的变化而变得不均匀。为了提高划分网格的精度要求,文献[9]利用纬度带上采样的网格点数与该纬度的余弦成正比加以修正,在不增加计算量的前提下使得网格划分区域更加均匀;为了突出某些重点区域的覆盖性能,可以赋予某些重要采样点不同的权值,也可以通过文件输入网格点权值使选择更具灵活性。文献[10]设计了覆盖区域为-80°～+80°纬度带的卫星星座,采用赤道上经纬度相差3°、相邻网格点相距300 km以上的网格分布方法进行星座性能计算,且考虑了网格点覆盖判定中由于仿真时间间隔造成的误差,利用求解仿真步长时间内的覆盖区域改进了网格点覆盖判定算法,避免了出现不连续覆盖和重复覆盖的情况。文献[11]在低轨区域通信卫星星座设计中给出了一种基于网格点统计的星座性能评价准则,在网格点的划分上采用弧长代替角度的方法,有效解决了等经度分割会使网格点随纬度变化而分布不均的问题。

同时,网格法还存在计算量较大等问题,大大影响设计速度,因此,在星座设计过程中需根据目标精度设定合适间隔的网格点,提高设计效率。

2.2 星间链路

针对处在不同卫星覆盖区域内的用户如何进行通信的问题,建立卫星与卫星之间的通信链路(即星间链路)是十分必要的。星间链路的建立使得卫星通信系统独立于地面网络为全球用户提供移动通信服务成为可能,有效地解决了地面通信网未覆盖地区的通信问题,同时保证全球任何地区在发生重大自然灾害时可以正常进行通信。

星间链路的建立应根据任务需求设置不同的链路连通性,一般为强连接和弱连接。强连接是指卫星通信系统中任何一颗卫星可以通过直接或间接的方式与其他任何一颗卫星进行通信,弱连接则指在一定区域内的卫星可以进行通信或在一段时间内部分卫星可以进行通信。由于卫星星座构型对星间链路有决定性的影响[12],比如:决定了两颗卫星能否建立链路、建立链路的难易程度以及链路性质,因此,在构建通信星座优化模型时需要将星间链路当作设计目标或约束条件加以分析,如:最大化星间链路数[4]、星座满足全连通[13]、永久星间链路约束[14]等。

星间链路的建立会受到多种因素的影响和限制,并且对链路的仰角、方位角和距离都有一定的要求。针对在一定约束条件下建立星间链路的问题,文献[4]在Flower星座模型的基础上设计了具有星间链路的通信卫星星座,在建立星间链路时以星间链路至少离地面500 km为约束条件,假设天线可以指向任意方向,得到了在相同卫星数目下覆盖性能与星间链路可建率均优于Walker星座模型的结论。同时,构建星间链路还需考虑维持时间等问题。文献[15]针对该问题研究了制约星座中任意两颗卫星构建静态星间链路(永久星间链路)三个主要因素:两颗卫星在其整个运行周期内是否一直可视;链路的指向变化是否在卫星天线跟踪角度、角速度变化范围之内;两颗卫星的相对速度在其连线上的投影是否在给定的范围内。文献[16]以Walker星座整体为设计对象,将文献[15]中的星间链路设计准则和星座全连通作为设计目标,根据星座一体化设计中的层次约束准则,与星座覆盖性能和系统成本同时进行优化设计,得到了特定任务要求下综合性能更优的星座方案,但只是讨论了在单层Walker星座构型下的星间永久链路构建的判断流程,并没有给出数值仿真结果。针对该问题,文献[14]通过对卫星轨道运动方程的分析、数值仿真得到了建立永久星间链路的普遍适用的方法,解决了不同轨道面、轨道高度卫星之间相对移动造成的星间链路频繁重构问题,为建立具有稳定网络拓扑结构的卫星星座提供了可能。文献[17]在分析两颗圆轨道卫星之间的相对运动关系的基础上,给出了构建永久星间链路可视条件的解析表达式,两颗卫星轨道高度r1和r2、倾角i、相位差α应满足

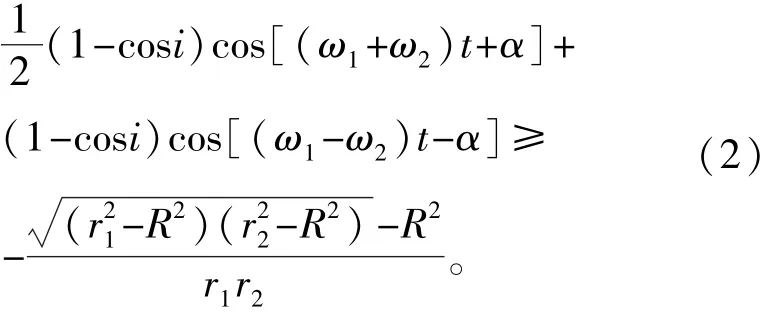
式中:R为地球半径。在多层卫星星座优化设计中,可以将永久可视条件作为约束,构建具有永久星间链路的卫星星座,使得整个网络具有较高的星间连接度,从而提高网络的稳定性。

建立两颗卫星的永久星间链路对卫星星载天线提出了极高的要求,建立链路的两颗卫星的天线必须始终准确地指向对方,星载天线应具备严格的实时自动调整跟踪功能,当星座中某颗卫星损毁或者失效则会造成系统的大面积瘫痪,抗毁能力差。同时,现有的星间链路设计还缺少对星间距离、星载设备发射功率对构建星间链路的影响分析,与构建实际卫星通信系统中的星间链路有较大的差距。

2.3 系统成本

受到经济实力和商业竞争的影响,当前的卫星系统已经不再不计成本地追求性能,“快、好、省”的设计理念被广泛接受[18],因此,在星座设计过程中加入对成本的分析是十分必要的。文献[19]将星座发射费用因子作为目标函数,发射费用因子定义为

式中:P为轨道面数;P0为轨道面数下限;i为轨道倾角;h为轨道高度;h0为轨道高度下限。该方法仅是粗略地分析了影响星座发射费用的因素(星座轨道面数、轨道倾角和轨道高度),并没有考虑卫星的建造成本。文献[20]利用多目标优化算法进行导航星座系统设计时,将导航精度和系统成本作为目标函数,分析影响系统成本的各个要素,主要包括发射费用、运载工具费用以及小卫星的成本。该文将导航精度和系统成本综合考量,设计出了性能优良且成本相对较低的导航星座。文献[21]建立了包含卫星生产成本和卫星发射成本的星座成本模型,提出了一种将星座性能和星座成本作为目标函数的导航星座优化方法。该模型比较简单,易于实现,但离实际情况相差较大。文献[22]同时分析了系统成本和星座覆盖性能对星座设计的影响,建立了包含卫星购置成本、系统维护成本、卫星发射成本的系统成本模型,设计了满足全球覆盖和系统成本约束下的卫星星座。文献[23]建立了复杂的成本计算模型,包括研发成本、星载设备成本以及不同运载火箭的发射成本,很好地将系统成本与星座性能联系在一起,为考虑系统成本的星座设计提供了良好的借鉴。

综上,构建星座设计优化模型需要结合实际系统要求,在覆盖性能、星间链路等多方面建立多个目标和约束函数,同时建立包含卫星平台、有效载荷、卫星发射、系统维护等因素的星座成本模型并将其融入优化模型中,以期获得更符合实际需求的星座设计方案。

3 优化算法

通信卫星星座设计优化模型的建立综合了多个方面因素,优化变量数目较多,且同时存在离散和连续形式,目标函数数量较多,而且存在多个非线性目标函数,这使得模型求解困难,采用传统寻优方法(如:爬山法、求导数法等)不能有效解决,需要采用现代优化算法求解。现代优化算法是模拟生物进化过程或某种物理现象的随机搜索算法,具有应用范围较广、搜索速度快且易于获得最优解等优点,在多目标多约束的优化问题中得到了广泛的应用。本节主要介绍卫星星座设计中常用的几种优化算法及其优缺点。

3.1 NSGA-II算法

1994年,Srinivas和Deb提出了非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA)[24]。该算法的优点是优化目标的数目不限,非劣最优解分布均匀,允许存在多个不同的等价解;缺点是计算复杂度较高,需要人为指定对优化结果影响较大的共享半径参数。

针对这些缺点,Ded进行了改进,提出了带精英策略的非支配排序遗传算法(NSGA-II)[25]。该算法将每个个体按照他们的支配与非支配关系进行分层,采用拥挤度距离即目标空间上每一点与同级别相邻两点之间的局部密度,代替了需要指定共享半径的适应度共享策略。在进行选择操作时,同时计算了每一个体的非劣等级和局部拥挤距离,如果两个个体的非劣等级不同,取等级高的个体;如果两个个体在相同等级上,则选取局部拥挤距离值大的个体,以使种群中的个体朝非劣解和均匀散布的方向进化,其流程图如图1所示。NSGA-II不需要外部存储,采用将父代和子代全部合并成一个统一种群的精英保留策略,算法的计算效率更高。优越的性能使得NSGA-II在过去几年得到了广泛应用和发展,相较其他的优化算法占据着主导地位。

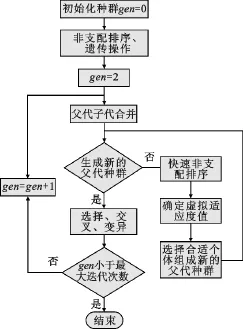
图1　NSGA-Ⅱ流程图[26]Fig.1 The flow chart of NSGA-Ⅱ

文献[28]利用NSGA-Ⅱ算法设计了地球区域观测卫星星座,同时考虑区域覆盖和分辨率两个方面,包含3个目标函数,即最大回访时间、区域权重回访时间和最大图像分辨率。对区域内网格点进行重访统计时采用连续计算的方式,由于变量空间的微小变动就能引起目标空间较大的波动,染色体的二进制编码可能会淘汰潜在的最优解,就需要在变量设计时采用近连续的编码方式,因此,采用了染色体实数编码方式代替二进制编码方式。

文献[29]提出了3颗卫星的区域覆盖星座设计方案,将最大回访时间(Maximum Revisit Time, MRT)和平均回访时间(Average Revisit Time,ART)的最小化作为目标函数,采用二进制编码的NSGA-Ⅱ算法进行优化求解,在进行并行处理时,在算法性能方面孤岛(Island)模式要好于主仆(Master-slave)模式的并行多目标优化算法(Parallel Multi-objective Evolutionary Algorithm,PMOEA)。

文献[30]提出了采用基于NSGA-Ⅱ算法进行区域覆盖侦察卫星星座优化设计方法,以重点目标的最大访问时间间隔、重点地面目标的分辨率和卫星数目为目标进行了仿真分析。对星座模型进行了简化,将卫星的6个轨道参数作为设计变量,在特定区域内满足覆盖要求。该方法加入多属性决策方法,可根据目标的重要程度作出相应选择,具有不需要设计目标权重、灵活性好等优点。

文献[31]对NSGA-Ⅱ算法进行了改进并应用于卫星星座设计,将反向学习机制(Opposition Based Learning,OBL)应用到NSGA-Ⅱ算法的进化过程中,并引入一种改进的算数交叉算子代替原有的模拟二进制交叉算子。改进的NSGA-Ⅱ算法在收敛速度、解的多样性上优于NSGA-Ⅱ算法,在区域覆盖卫星星座优化设计中具有良好的效果。

综上,NSGA-Ⅱ算法具有优化目标个数较多、最优解分布均匀、鲁棒性好等优点,但存在计算速度较慢、可能产生搜索偏移等问题。在星座设计中,搜索效率不是重要指标,设计者更关心能否得到最优解,因此,该算法在星座设计中得到了广泛的应用。

3.2 粒子群算法

Kennedy和Eberhart在1995年提出了粒子群算法(Particle Swarm Optimization,PSO)[27],算法的流程图如图2所示。粒子群算法易于实现,参数空间小,且采用的实数编码方式能较好的解决实值优化问题,对连续优化问题和离散优化问题都有较好的效果,但容易陷入局部最优,因此,对初始种群和学习因子的设定有较高的要求。粒子群算法的优势十分明显,实数编码的特点特别适合处理星座设计中的优化问题,但该算法容易陷入局部最优解,影响优化效率和优化结果,因此,可以引进类似遗传算法中的变异算子,使粒子在改变自己位置和速度时,可以以一定概率接受其他改变量,从而增加了候选解的多样性,避免了陷入局部最优解当中。

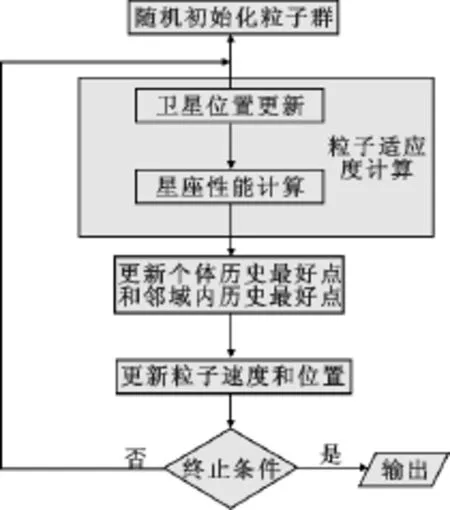
图2　粒子群算法流程图[27]Fig.2 The flow chart of PSO

文献[32]利用多目标粒子群算法(Multi-objective Particle Swarm Optimization,MOPSO)对导航星座进行优化设计,将星座中卫星数目、轨道面数目、轨道高度、倾角、相位等作为设计变量,导航性能和卫星生产成本作为目标函数,采用中轨(Medium Earth Orbit,MEO)和静止轨道(Geostationary Earth Orbit,GEO)卫星组成的混合星座,MEO星座采用Walker模型用于全球导航,GEO卫星则用于增强中国及周边地区的导航性能,对实际工程应用具有一定参考价值。

文献[33]对低轨道和椭圆轨道组成的混合卫星星座进行了研究,优化目标为满足覆盖要求的最小卫星数,约束条件为目标区域内至少是单重覆盖,提出了一种自适应变异的高效粒子群算法进行优化设计,得到了算法性能优于遗传算法和传统粒子群算法的结论。

综上,粒子群算法具有易于实现、参数少、搜索效率高等优点,且其实数编码的特点特别适合于处理星座优化问题,逐渐成为研究的热点。

3.3 其他算法

文献[11]在进行低轨区域通信星座的设计过程中,对遗传算法进行了改进,在基本遗传算法的基础上加入了复形调优算法,根据优化过程中优异解的分布对参数变化空间进行调整,提高了遗传算法对局部最优解的搜索能力。文献[34]建立了一种比较通用的3+4N(N为卫星数目)区域覆盖星座模型,使目标区域覆盖百分比最大化,采用遗传算法进行优化设计,使得星座设计具有较大的灵活性。

文献[20]利用Matlab中的多目标遗传算法工具箱和STK(Satellite Tool Kit)软件在不同轨道高度上设计全球导航卫星系统进行了探索研究,将系统成本和平均全球几何精度因子作为优化目标,分析了星座参数包括Walker星座参数和轨道参数,对所有的设计变量进行了一定的限制,根据不同的待测试模型调整各设计变量的取值范围,使算法获得了更加精确的解。

文献[35]利用增强Pareto优化算法(Strength Pareto Evolutionary Algorithm,SPEA)进行星座设计,并对算法进行了改进,提出了一种整数和浮点数混合的染色体编码方法,并在浮点数编码方式上引入了多体交叉和Cauchy变异的概念,增加了个体的多样性,加快了收敛速度,提高了效率。优化目标为指定区域的覆盖率最大化,约束条件为星间链路连通性。该方法的不足之处是计算时间较长,算法的效率较低,并且没有对连续覆盖的要求进行相关的约束设计。

文献[5]采用改进非支配紧邻免疫算法(Nondominated Neighbor Immune Algorithm,NNIA)对低轨混合星座进行优化设计,采用低轨混合星座提升覆盖均匀性,将平均重访时间和重访时间方差作为目标函数,约束条件为平均每天覆盖次数。将约束支配方法引入到NNIA算法中,使其具备了约束处理能力,得到了改进的NNIA算法在收敛速度和多样性上均优于NSGA-II算法和多目标粒子群算法(MOPSO),可大大提高星座设计效率的结论。

表1对本节算法进行了归纳总结。

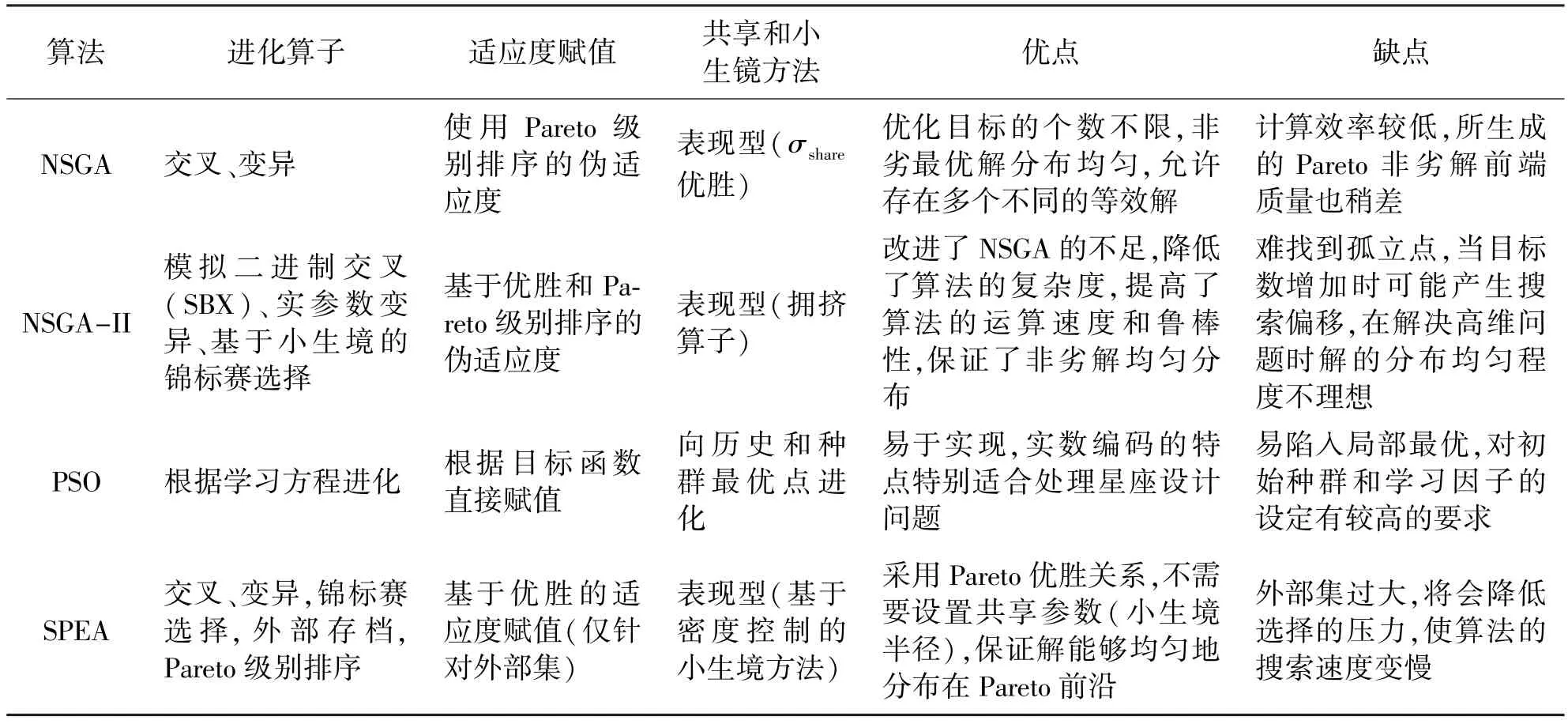
表1　主要多目标优化算法及其特征Tab.1 Multi-objective evolutionary algorithms and their characteristics

4 存在的问题与展望

传统的通信卫星星座设计模型主要研究了星座覆盖性能和简单的星间链路建立准则,覆盖主要面向全球或特定纬度带,对特定区域有效覆盖的研究较少,而星间链路的建立一般采用卫星可见即可建立星间链路的准则,没有考虑天线仰角、星间距离及方位角等问题,与实际建立星间链路的要求差距较大。其次,传统的通信卫星星座设计模型中包含的因素较少,缺少考虑通信卫星星座有效覆盖、星间链路要求、系统成本、星座容错性、可靠性等多个因素的综合设计,存在构建符合实际应用的优化模型难度较大等问题,因此,采用传统星座设计方法得到的设计结果往往难以满足实际系统的要求。

在星座优化模型求解方面,经典的优化算法理论基础薄弱,存在搜索时间较长且迭代效率不高、可能收敛到局部最优解、对参数设置比较敏感等问题,严重影响了其求解星座设计优化模型的效果。

综上所述,通信卫星性能与星座几何构型密切相关,因此,进行星座设计时首先应该设置满足任务要求的优化变量,然后考虑多个设计目标的建立(如:覆盖性能、通信性能、星间链路、系统成本、容错性、稳定性等),综合分析不同任务对这些目标的不同要求,设置合适的目标函数;其次,根据任务设定合适的约束条件,包括对卫星轨道高度的限定、星座层次结构的选择、系统成本限制等;最后,选择和设计适合该优化模型的现代优化算法对模型进行求解,得到综合性能最优的星座几何构型。

5 结束语

通信卫星星座优化设计的关键技术主要包括构建准确的与实际要求相符的优化模型以及设计求解效果和复杂度最佳折衷的优化算法。本文通过对通信卫星星座设计中覆盖性能、星间链路和系统成本三个方面的研究分析,表明了构建符合实际应用的星座优化模型需要综合多个设计因素,并选择合适算法进行优化求解。下一步应结合具体的星座系统建设任务,根据实际的目标要求和约束条件建立准确的星座设计优化模型,构建通信星座模拟仿真系统对星座性能进行综合评估,并依据评估结果对星座方案进行适当调整。星座优化设计结果给出了当前目标和约束条件下系统理论性能达到最优的星座方案,为确定实际系统最终的星座方案提供了参考和改进的方向。

[1] 肖楠,梁俊,张基伟.中国低轨卫星星座组网设计与规划[J].电讯技术,2010,50(12):14-17. XIAO Nan,LIANG Jun,ZHANG Jiwei.Design and scheme of China′s LEO satellite constellation network [J].Telecommunication Engineering,2010,50(12):14-17.(in Chinese)

[2] WHITTECAR W R,FERRINGER M P.Global coverage constellation design exploration using evolutionary algorithms[C]//Proceedings of 2014 AIAA/AAS Astrodynamics Specialist Conference.San Diego:AIAA,2014: 107-113.

[3] 魏蛟龙,岑朝辉.基于蚁群算法的区域覆盖卫星星座优化设计[J].通信学报,2006,27(8):62-66. WEI Jiaolong,CEN Chaohui.Optimization of regional coverage satellite constellations based on ant colony algorithm[J].Journal on Communications,2006,27(8):62-66.(in Chinese)

[4] DANIELE M,MAURO D S,MARCO L.Design of flower constellations for telecommunication services[J].Proceedings of the IEEE,2011,99(11):2008-2019.

[5] 姜兴龙,姜泉江,刘会杰,等.采用改进非支配近邻免疫算法的低轨混合星座设计优化[J].宇航学报, 2014,35(9):1007-1014. JIANG Xinglong,JIANG Quanjiang,LIU Huijie,et al.Design optimization of hybrid LEO constellation using modified non -dominated neighbor immune algorithm[J].Journal of Astronautics,2014,35(9):1007-1014.(in Chinese)

[6] MA D M,HONG Z C,LEE T H,et al.Design of a microsatellite constellation for communication[J].Acta Astronautica,2013(1):54-59.

[7] 李赞,张乃通.卫星移动通信系统星间链路空间参数分析[J].通信学报,2000,21(6):92-96. LI Zan,ZHANG Naitong.ISL spacial paremeters analysis of mobile satellite communication system[J].Journal on Communications,2000,21(6):92-96.(in Chinese)

[8] RIDER L.Analytic design of satellite constellations for zonal earth coverage using inclined circular orbits[J].Journal of the Astronautical Sciences,1986,34(1):31-64.

[9] 韩潮,邓丽,徐嘉.星座覆盖性能评估的改进网格点仿真法[J].计算机仿真,2005,22(12):21-23. HAN Chao,DENG Li,XU Jia.Improved grid simulation for constellation coverage performance evaluation[J].Computer Simulation,2005,22(12):21-23.(in Chinese)

[10] 黄凤娟.均匀时相低轨卫星星座的设计与仿真[D].北京:北京邮电大学,2008:40-56.HUANG Fengjuan.Design and simulation based on low -orbit constellations with even temporal phases[D]. Beijing:Beijing University of Posts and Telecommunications,2008:40-56.(in Chinese)

[11] 郦苏丹,朱江,李广侠.采用遗传算法的低轨区域通信星座优化设计[J].通信学报,2005,26(8):122-128.LI Sudan,ZHU Jiang,LI Guangxia.Optimization of LEO regional communication satellite constellation with GA algorithm[J].Journal on Communications,2005,26 (8):122-128.(in Chinese)

[12] 罗大成,刘岩,刘延飞,等.星间链路技术的研究现状与发展趋势[J].电讯技术,2014,54(7):1016-1024. LUO Dacheng,LIU Yan,LIU Yanfei,et al.Present status and development trends of inter-satellite link[J].Telecommunication Engineering,2014,54(7):1016-1024. (in Chinese)

[13] 范丽.卫星星座一体化优化设计研究[D].长沙:国防科学技术大学,2006:4-8.FAN Li.Study on integrated design optimization of satellite constellation[D].Changsha:National University of Defense Technology,2006:4-8.(in Chinese)

[14] 王振永,王平,顾学迈,等.卫星网络中永久星间链路的设计方法研究[J].通信学报,2006,27(8):129-133.WANG Zhenyong,WANG Ping,GU Xuemai,et al.Research on design of permanent inter-satellite-links in satellite networks[J].Journal on Communications,2006, 27(8):129-133.(in Chinese)

[15] SHAH N H.Automated station-keeping for satellite constellations[D].Massachusetts:Massachusetts Institute of Technology,1997.

[16] 范丽,张育林.Walker星座星间链路构建准则及优化设计研究[J].飞行力学,2007,25(2):93-96.FAN Li,ZHANG Yulin.Construction rules and design optimization of ISLs in Walker constellations[J].Flight Dynamics,2007,25(2):93-96.(in Chinese)

[17] 王沈泽,晏坚,陈翔,等.多层卫星网络构型优化中的永久星间链路可视条件[J].兵工学报,2014,35 (S1):115-121.WANG Shenze,YAN Jian,CHEN Xiang,et al.Visual conditions of permanent inter-satellite links in the design of multi-layered satellite networks[J].Acta Armamentarii,2014,35(S1):115-121.(in Chinese)

[18] 陈琪峰.飞行器分布式协同进化多学科设计优化方法研究[D].长沙:国防科技大学,2007:23-40.CHEN Qifeng.Distributed coevolutionary multidisciplinary design optimization methods for flying vehicles [D].Changsha:National University of Defense Technology,2007:23-40.(in Chinese)

[19] 谢恺,薛模根,韩裕生,等.基于遗传算法的低轨天基雷达星座设计[J].信号处理,2008,24(2):233-236. XIE Kai,XUE Mogen,HAN Yusheng,et al.LEO space-based radar constellation design based on a genetic algorithm[J].Signal Processing,2008,24(2):233-236. (in Chinese)

[20] JENNINGS A L,DINIZ H.Global navigation satellite system design exploration using a multi-objective genetic algorithm[C]//Proceedings of 2013 Space Conferences and Exposition.Pasadena:AIAA,2013:1-5.

[21] 刘欣,路辉,陈晓.基于分解思想的导航星座多目标优化[J].微计算机信息,2012,28(9):214-216. LIU Xin,LU Hui,CHEN Xiao.Optimization of navigation constellation by a multi-objective evolutionary algorithm based on decomposition[J].Microcomputer Information,2012,28(9):214-216.(in Chinese)

[22] CLIFFORD K,MAGED D.Minimizing the cost of availability of coverage from a constellation of satellites:evaluation of optimization methods[J].Systems Engineering,2004,7(2):113-122.

[23] 常辉.卫星星座协同优化设计研究[D].武汉:华中科技大学,2012:32-42. CHANG Hui.Study on collaborative optimization design of satellite constellation[D].Wuhan:Huazhong University of Science and Technology,2012:32-42.(in Chinese)

[24] SRINIVAS N,DEB K.Multiobjective optimization using nondominated sorting in genetic algorithms[J].Evolutionary Computation,1994,2(3):221-248.

[25] DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2): 182-197.

[26] 曾喻江.基于遗传算法的卫星星座设计[D].武汉:华中科技大学,2007:83-98. ZENG Yujiang.Satellite constellation design based on genetic algorithm[D].Wuhan:Huazhong University of Science and Technology,2007:83-98.(in Chinese)

[27] KENNEDY J,KENNEDY J F,EBERHART R C,et al. Swarm intelligence[M].San Francisco:Morgan Kaufmann,2001:8-35.

[28] MATTHEW P F,DAVID B S.Satellite constellation design tradeoffs using multiple-objective evolutionary computation[J].Journal of Spacecraft and Rockets,2006, 43(6):1404-1411.

[29] FERRINGER M P,CLIFTON R S,THOMPSON T G.Efficient and accurate evolutionary multi-objective optimization paradigms for satellite constellation design[J].Journal of Spacecraft and Rockets,2007,44(3):682-691.

[30] 王励,王炎娟,张辉,等.基于NSGA-II算法的区域覆盖卫星星座优化[J].计算机仿真,2009,26(4):80-84. WANG Li,WANG Yanjuan,ZHANG Hui,et al.Optimization of regional coverage reconnaissance satellite constellations by NSGA-Ⅱ algorithm[J].Computer Simulation,2009,26(4):80-84.(in Chinese)

[31] 肖宝秋,刘洋,戴光明.改进的NSGA-II算法及其在星座优化设计中的应用[J].计算机工程与应用, 2012,48(10):47-53. XIAO Baoqiu,LIU Yang,DAI Guangming.Improved NSGA-II algorithm and its application in optimization of satellite constellation[J].Computer Engineering and Applications,2012,48(10):47-53.(in Chinese)

[32] 蒙波,伊成俊,韩潮.基于多目标粒子群算法的导航星座优化设计[J].航空学报,2009,30(7):1285-1291. MENG Bo,YI Chengjun,HAN Chao.Optimization of navigation satellite constellation by multi-objective particle swarm algorithm[J].Acta Aeronautica et Astronautica Sinica,2009,30(7):1285-1291.(in Chinese)

[33] 蒙波,韩潮.基于改进粒子群算法的混合卫星星座优化设计[J].上海航天,2010,27(1):36-39. MENG Bo,HAN Chao.Optimization of hybrid constellation by modified particle swarm algorithm[J].Aerospace Shanghai,2010,27(1):36-39.(in Chinese)

[34] 王瑞,马兴瑞,李明.采用遗传算法进行区域覆盖卫星星座优化设计[J].宇航学报,2002,23(3):24-28. WANG Rui,MA Xingrui,LI Ming.Optimization of regional coverage satellite constellations by genetic algorithm[J].Journal of Astronautics,2002,23(3):24-28. (in Chinese)

[35] 刘文,张育林,刘昆.基于多目标进化算法的卫星通信星座优化设计[J].宇航学报,2008,29(1):95-99. LIU Wen,ZHANG Yulin,LIU Kun.Optimization of multi-objective evolutionary algorithm based communication satellite constellation[J].Journal of Astronautics, 2008,29(1):95-99.(in Chinese)

莫 宇(1992—),男,四川成都人,2014年于电子科技大学获硕士学位,现为国防科学技术大学硕士研究生,主要研究方向为卫星通信与星座设计;

MO Yu was born in Chengdu,Sichuan Province,in 1992.He received the B.S.degree from University of Electronic Science and Technology of China in 2014.He is now a graduate student.His research concerns satellite communication and constellation design.

Email:405070026@qq.com

闫大伟(1986—),男,陕西西安人,2010年于空军工程大学获硕士学位,现为国防科学技术大学博士研究生,主要研究方向为卫星通信与星座设计;

YAN Dawei was born in Xi′an,Shaanxi Province,in 1986.He received the M.S.degree from Air Force Engineering University in 2010.He is currently working toward the Ph.D.degree.His research concerns satellite communication and constellation design.

Email:yandawei_1986@163.com

游 鹏(1983—),男,江西丰城人,2014年获博士学位,现为讲师,主要研究方向为卫星通信与网络;

YOU Peng was born in Fengcheng,Jiangxi Province,in 1983. He received the Ph.D.degree in 2014.He is now a lecturer.His research concerns satellite communication and network.

Email:ysw_nudt@vip.126.com

雍少为(1965—),男,重庆人,1997年获博士学位,现为研究员。

YONG Shaowei was born in Chongqing,in 1965.He received the Ph.D.degee in 1997.He is now a senior engineer of professor.

A Survey of Constellation Optimization Design for Satellite Communications

MO Yu,YAN Dawei,YOU Peng,YONG Shaowei
(School of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)

Constellation optimization design for satellite communications is one of the key steps to construct a communication system.The methods of constellation design are divided into optimization model and evolutionary algorithms,and the prospect is brought forward.Firstly,a general optimization model for the constellation design of satellite communication is proposed and the methods of setting up the optimization variables,objective functions and constraint conditions are introduced from three aspects of coverage performance,inter-satellite links and cost of system.Then three kinds of multi-objective algorithms in satellite constellation design are stated,and characteristics of four algorithms are summarized.Meanwhile,their merits and drawbacks are compared in satellite constellation design.Finally,problems in constellation design are pointed out and future research directions are forecasted.

satellite communication;constellation design;inter-satellite link;multi-objective optimization; evolutionary algorithm

1 引 言

卫星星座设计是卫星系统建立的前提和关键,目标是要得到星座卫星数目和每个卫星的6个轨道参数,即轨道面的半长轴r、离心率e、倾角i、近地点幅角w、升交点赤经Ω和平近点角f。为了得到性能优异的星座构型,通常需要根据任务要求确定这些参数。卫星系统任务涉及多个目标和多个约束,如覆盖性能、通信性能、星间链路、系统成本、容错性、稳定性等[1],因此,卫星星座设计是多目标多约束的优化问题,即寻找满足多种约束条件下使目标函数最优的星座构型参数。

**通信作者:ysw_nudt@vip.126.com ysw_nudt@vip.126.com

TN927

A

1001-893X(2016)11-1293-08

10.3969/j.issn.1001-893x.2016.11.020

2016-03-18;

2016-08-01

date:2016-03-18;Revised date:2016-08-01

引用格式:莫宇,闫大伟,游鹏,等.通信卫星星座优化设计综述[J].电讯技术,2016,56(11):1293-1300.[MO Yu,YAN Dawei,YOU Peng,et al. A survey of constellation optimization design for satellite communications[J].Telecommunication Engineering,2016,56(11):1293-1300.]