曲线钢-混叠合梁架设及顶升分析

李泉彬

(广东省交通规划设计研究院股份有限公司，广东 广州 510507)



曲线钢-混叠合梁架设及顶升分析

李泉彬

(广东省交通规划设计研究院股份有限公司，广东 广州 510507)

钢混叠合箱梁通常使用槽型钢梁，连续梁的中支点临时顶升法可为该位置的混凝土桥面板提供预压力，当桥梁为曲线时，在施工过程中槽型钢箱会产生扭转变形甚至畸变，进而影响架设安全及预压力效果。通过分析槽型钢-混组合梁在各关键工况下的受力和变形，探讨合理的构造设计及顶升方式。

槽型钢混叠合梁；曲线梁；顶升；扭转变形；预加压力

1 模型建立

本文以1座跨径为33 m+35 m的钢-混组合梁桥为例,桥梁平曲线半径R为130 m,槽型钢梁高H为1.45 m,箱宽B为2.7 m,上翼缘板宽T为0.6 m,混凝土顶板厚为0.32 m,钢箱内每隔3 m设置1道横隔板,截面底板厚为24 mm,上翼板厚为30 mm,腹板厚为18 mm。

利用空间有限元分析软件Midas/Civil 2012建立空间模型,钢板采用薄板单元模拟,混凝土板采用厚板单元模拟。组合梁断面如图1所示。

图1 钢-混叠合梁断面图

2 分析方法及要点

曲线钢梁在自重、混凝土重量及顶升力的作用下,均会产生自由扭转变形及约束扭转变形,2种扭转变形都假定截面周边保持不变形,为刚体转动。当钢板较薄或横隔板较少时,截面还会发生畸变[1]。开口截面扭转惯性矩远小于闭口截面,非常容易发生畸变产生翘曲应力。

为了考察该座开口箱梁在施工过程中的扭转变形和扭转应力,建立带横隔板的开口箱梁空间板单元有限元模型,与等尺寸的闭合箱梁模型、无横隔板开口箱梁模型进行扭转变形对比,验证横隔板的设置合理性,以使开口钢箱保持整体扭转,保证施工过程的结构安全[2]。

另外,两孔连续钢-混叠合梁结构,通常通过顶升钢梁中支点-浇筑顶板混凝土-叠合梁回落工序,使中支点顶板混凝土产生预压应力[3-4]。本文提出单支点顶升、等位移双支点顶升及不等位移双支点顶升3种顶升方法,通过对比各工况下弯梁的应力,寻求合理的顶升方式。

3 箱梁架设时的扭转变形

对于扭转变形,可以使用箱室4个角点的水平位移(Y)、竖向位移(Z)描述,如图2所示。而利用节点位移,推算出腹板转角α=arctan((Y1-Y2)/H)和底板转角β=arctan((Z1-Z2)/B)[5]。当α、β较接近时,说明箱梁发生自由扭转和约束扭转,接近刚体转动。当α、β相差较大时,说明箱梁的翘曲变形较大。

图2 箱梁扭转变形示意图

(1) 闭口无隔板箱梁的扭转变形。建立与示例桥梁等尺寸的闭合箱梁模型,且仅在支座位置设置支承隔板,在箱梁吊装工况下,受自重力作用,提取关键截面的角点位移,计算出α、β数值[6],计算结果如图3所示。其中横坐标为截面号,1#～46#为33 m跨,46#～91#为35 m跨,1#、46#、91#截面为支点截面,竖坐标为板的扭转角度(下同)。

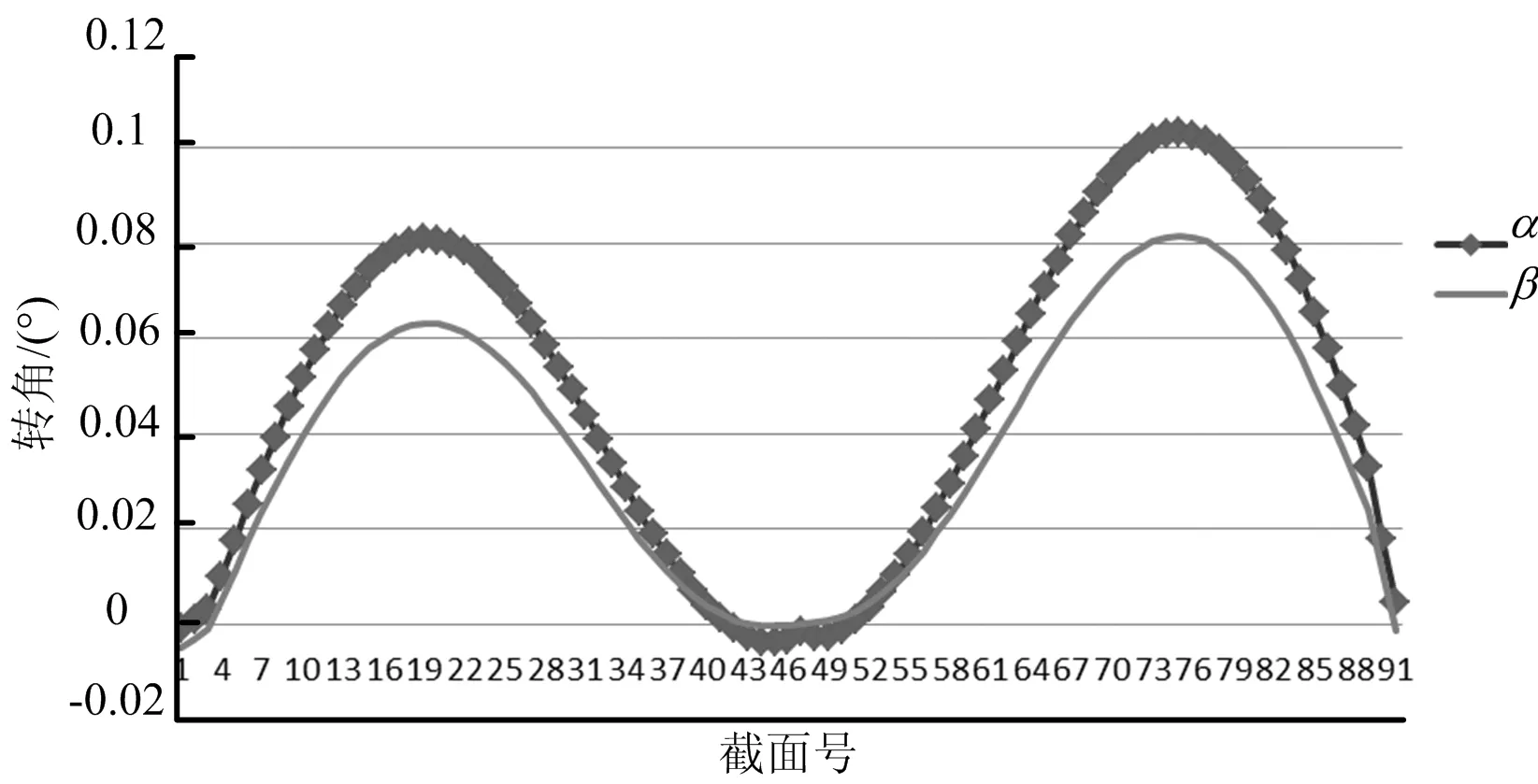
图3 闭合箱梁自重下的扭转变形

闭合箱梁腹板最大扭转角度约为0.10°,底板最大扭转角约为0.08°, 35 m跨的扭转变形大于33 m跨;支点位置的α、β值接近,而跨中位置的α、β值相差约为0.02°,α/β最大值为1.25,说明设置横隔板的支点截面接近刚体转动,未设置横隔板的截面发生一定程度的翘曲变形;曲线图普遍表现为α>β,这是底板较厚,其刚度较大,较之腹板不容易发生翘曲变形的表现[7]。

(2) 开口无隔板箱梁的扭转变形。建立开口箱梁模型,仅在支座处设置支承隔板,计算结果如图4所示。

图4 开口无隔板箱梁自重下的扭转变形

开口箱梁腹板最大扭转角度约为0.94°,底板最大扭转角约为0.12°,均比闭合箱梁大,其扭转刚度比闭合箱梁大幅降低;跨中最大α/β=0.94/0.12=7.83,转角曲线差异非常大,说明无侧向约束的腹板发生较大的扭转翘曲变形,箱梁畸变严重。

(3) 带隔板开口箱梁的扭转变形。建立开口带隔板箱梁模型,每孔各布置11道横隔板,计算结果如图5所示。

图5 带隔板开口箱梁自重下的扭转变形

该箱梁腹板、底板最大扭转角度约为0.17°,均比闭合箱梁稍大,说明其扭转刚度能接近闭合箱梁,但依然比闭合箱梁小;α、β曲线基本重合,说明箱梁非常接近于整体扭转,翘曲变形非常小,横隔板的设置保证了施工期间开口箱梁稳定性及安全性。

4 钢-混叠合梁顶升-回落应力分析

中支点3种顶升方法的顶升高度均控制在125 mm,通过空间有限元模型,计算出浇筑混凝土时钢梁翼缘应力σs1、σs2及回落后混凝土板的压应力σC1、σC2,对比3种方法的计算结果,判断顶升方法的优劣[8-9]。

(1) 单支点顶升。顶升中支点底板中心位置,顶升高度为125 mm,计算出此工况下的σs1、σs2、σC1、σC2数值,计算范围为中支点前后各4 m。

计算结果见表1所列。

表1 各工况钢梁与混凝土板应力计算结果

由表1可见,钢梁内侧上翼缘最大拉应力σs1为155.2 MPa,外侧上翼缘最大拉应力σs2为184.1 MPa,外侧上翼缘应力较大,内外侧差值为28.9 MPa。

叠合梁回落后混凝土面板内侧最小压应力σC1为2.3 MPa,外侧面板最小压应力σC2为1.9 MPa,外侧混凝土板压应力储备较小,内外侧差值为0.4 MPa。

(2) 双支点等位移顶升。顶升方式调整为中支点底板两侧边缘位置,顶升高度为125mm,由表1可见,σs1为181.2 MPa,σs2为178.4 MPa,内外侧应力较均衡,且最大应力比单支点顶升略有下降。σC1为3.3 MPa,σC2为3.1 MPa,外侧混凝土板压应力储备略小,内外侧差值为0.2 MPa。

(3) 双支点不等位移顶升。顶升方式调整为中支点底板两侧边缘位置,内侧顶升高度为120 mm,外侧顶升高度为130 mm,由表1可见,σs2为175.6 MPa,较之双支点等位移顶升进一步下降。σC1为3.1 MPa,σC2为3.2 MPa,内外侧混凝土板压应力储备基本一致。

5 结 论

(1) 通过合理设置横隔板,开口箱梁可大幅提高箱梁的整体抗扭刚度,但比其闭合箱梁依然较小,故扭转变形应予以重视。

(2) 无论是开口箱梁还是闭合箱梁,横隔板对减少箱梁的翘曲变形均有必要,尤其是开口钢梁,设置合理的横隔板将大幅提高其截面整体性。

(3) 跨中位置发生翘曲变形的潜在可能性最大,故该位置应至少设置1道横隔板。

(4) 单支点顶升法,扭转变形使叠合梁内外侧应力差异较大,回落时有一部分竖向位移是截面旋转分量,不产生弯曲应力,故其压应力储备较小;双支点等位移顶升时,内侧比外侧弯曲变形大,故内侧的钢梁应力及混凝土预压力均比外侧大。

(5) 双支点不等位移顶升法,通过调整2个支撑点的顶升量,控制梁的扭转变形及弯曲变形,可获得较为均衡、合理的钢梁施工期间应力水平及混凝土桥面板预压应力。

[1] 吴 冲.现代钢桥(上)[M].北京:人民交通出版社,2006.

[2] 刘玉擎.组合结构桥梁[M].北京:人民交通出版社,2005.

[3] 聂建国.钢-混凝土组合结构桥梁[M].北京:人民交通出版社,2011.

[4] 张景坤，徐克敏．钢-混凝土结合梁顶升施工技术[J].上海建设科技,2008(11):16～18.

[5] 余茂峰,刘君波,叶建龙.曲线开口钢箱的扭转变形及横隔板合理间距分析[J].公路交通技术,2011(4):22～25.

[6] 胡 强,陈浩军,王季青.空间曲线钢箱梁有限元分析[J].公路与汽运,2004(3):51～53.

[7] 王 猛.钢-混凝土连续组合梁的设计分析[J].城市道桥与防洪,2014(12):53～55.

[8] JTG D64-2015,公路钢结构桥梁设计规范[S]．

[9] JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S]．

2016-05-12；修改日期：2016-05-23

李泉彬(1985-)，男，广东新会人，广东省交通规划设计研究院股份有限公司工程师．

U448.216

A

1673-5781(2016)03-0407-03