函数在谓词逻辑符号化中的应用

孙翠先

(唐山学院 基础教学部，河北 唐山 063000)



函数在谓词逻辑符号化中的应用

孙翠先

(唐山学院 基础教学部，河北 唐山 063000)

针对不同个体域，用实例讨论了谓词逻辑中命题符号化时函数的引入、函数的作用以及谓词和函数的区别，并给出了错误使用函数的例子，分析了产生错误的原因。

个体域；谓词逻辑；函数；命题符号化

0 引言

将自然语言中的命题用逻辑符号表示成谓词公式，即符号化，也称作翻译。谓词是用来刻画个体词性质及个体词之间相互关系的词[1]，谓词逻辑符号化时，经常需要引入函数，而函数是值域为个体域的映射。

谓词逻辑是数理逻辑的重要部分，而数理逻辑在“离散数学”课程中起着非常重要的作用。数理逻辑用抽象的符号表达各种推理，很多思维过程可以用谓词符号化，使之能进行数学运算。

命题符号化及推理一直是“离散数学”教学研究的热门问题。文献[2]研究了符号化时量词与联结词的搭配，文献[3]讨论了同一命题在不同个体域上可以有不同的符号化形式，文献[4]举例说明了谓词的选用影响翻译，文献[5]给出了关于量词交换的条件。本文将通过实例讨论谓词符号化时函数所起的作用，以及如何恰当地使用函数。谓词符号化本身没有唯一标准，能使谓词公式简单、准确是唯一的目的。

1 定义

设D为个体域，它是个体词组成的集合，可以是有限集，也可以是无限集。

定义1 称D×D×…×D到D的一个映射叫作n元函数(D≠Φ)，函数用小写英文字母表示。

设f(x1，x2，…，xn)是一个n元函数，从定义1可知，f的定义域为D×D×…×D=Dn，值域为D。

定义2 称D×D×…×D到V={0，1}的一个映射叫做n元谓词(D≠Φ)，谓词用大写英文字母表示。

设P(x1，x2，…，xn)是一个n元谓词，从定义2可知，它不是命题，因为不能确定其真值。只有当x1，x2，…，xn取定D×D×…×D=Dn一组个体时，谓词P就转化为命题，此时具有真假意义，它的值不是0就是1，这里，0=假，1=真。谓词P的定义域为D×D×…×D=Dn，值域为V={0，1}。

2 命题符号化

以下给出实例，并将命题翻译成谓词公式，从中体现函数的作用，同时区别函数和谓词是两个完全不同的概念。

2.1 公式中含有一元函数，考虑两个不同的个体域

命题1 存在二阶方阵A，使得A×A=A2=I。

将命题1翻译成谓词公式，涉及一元谓词和一元函数，其中“=”需引入谓词，运算“A2”需引入函数。为此取字头E表示“相等”，令谓词E(x)等于二阶单位阵I，令函数s(x)=x2。符号化为∃AE(s(A))。

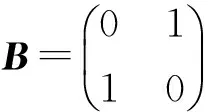
若不引入函数，直接令谓词E(x)：x2等于二阶单位阵I，符号化为∃AE(A)，这时不能体现命题1内在的逻辑关系，掩盖了命题所要表达的矩阵运算。

命题2 方程x3-4x2+1=0在区间(0，1)内至少有一个实根。

将命题2翻译成谓词公式时，涉及二元谓词和一元函数，其中“=”“>”需引入二元谓词，运算“x3-4x2+1”需引入函数，同时指派常量。为此取字头E表示“相等”，令谓词E(x，y)：x=y，G表示“大于”，令G(x，y)：x>y，令函数f(x)=x3-4x2+1，常量a：0，常量b：1。

符号化为∃x(G(x，a)∧G(b，x)∧E(f(x)，a))。

这里个体域D是所有实数组成的集合，应用高等数学中零点存在定理很容易证明x的存在性，这里不再重述，但x的精确值很难求出。因为在D内存在x，即公式∃x(G(x，a)∧G(b，x)∧E(f(x)，a))存在一个解释，使其真值为1，因此公式是真命题。可以看出二元谓词是用来刻画个体词之间相互关系的，对个体词指派后它有真值。而这里的函数描述了个体词的运算，无论如何指派，其无真假意义。只有借助函数，才能将x3-4x2+1符号化，深刻解释命题描述是一元三次方程的根。

至于x的精确值没有给出，怀疑公式真值为1，也可以理解。下面借助Matlab软件给出零点的精确值和存在性。

命令：>>solve('x^3-4*x^2+1')

根：ans=

1/6*(404+12*i*687^(1/2))^(1/3)+32/3/(404+12*i*687^(1/2))^(1/3)+4/3

-1/12*(404+12*i*687^(1/2))^(1/3)-16/3/(404+12*i*687^(1/2))^(1/3)+4/3+1/2*i*3^(1/2)*(1/6*(404+12*i*687^(1/2))^(1/3)-32/3/(404+12*i*687^(1/2))^(1/3))

-1/12*(404+12*i*687^(1/2))^(1/3)-16/3/(404+12*i*687^(1/2))^(1/3)+4/3-1/2*i*3^(1/2)*(1/6*(404+12*i*687^(1/2))^(1/3)-32/3/(404+12*i*687^(1/2))^(1/3))

命令：>>ezplot('x^3-4*x^2+1'，[0，1])，[0，1]内图形。

零点存在图见图1。

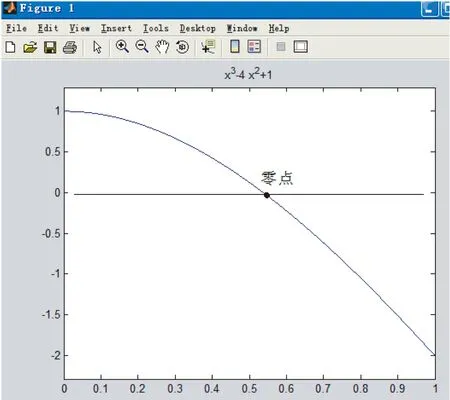
图1 零点存在图

2.2 公式中含有二元函数，考虑两个不同的个体域

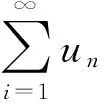
将命题3翻译成谓词公式，涉及二元谓词和二元函数，其中“正数ε”“n>N”“|Sn-s|<ε”，“正整数”需引入谓词，而运算“|Sn-s|”需引入函数。为此，取lessthan和greaterthan的字头L和G表示“小于”和“大于”。令谓词L(x，y)：xy，I(x)：x是在正整数，函数f(x，y)=|x-y|。

符号化为∀ε(G(ε，0)→∃N∀n((I(N)∧G(n，N))→L(f(Sn，s)，ε)))。

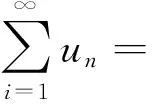
可以看出二元谓词是描述个体词之间相互关系的，对个体词指派后它有真值。而这里的函数描述了个体词间的运算，无论如何指派，其无真假意义。只有借助二元函数，才能将|Sn-s|符号化，因为运算|Sn-s|不是联结词。

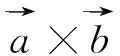
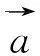
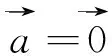
由命题4的翻译可以看出，这里的函数m(x，y)：x×y是一个二元运算，它具体的运算规则是在个体域D中进行的，对不同个体域D，函数运算规则不同。同样是乘法，在命题1中指矩阵相乘，在命题4中指向量的向量积。

2.3 一般地，公式中可以含有多元函数

命题5 方阵A可逆的充分必要条件是存在有限个初等阵P1，P2，…，Pl，使得A=P1P2…Pl。

这里个体域D是所有n阶矩阵组成的集合，其中“是方阵”“是初等阵”“是可逆”和“=”需引入谓词，“乘积”需引入函数。为此，取字头M表示“是方阵”、R表示“是可逆”、J表示“是初等阵”、E表示“相等”。令M(x)：x是方阵；R(x)：x是可逆的；J(x)：x是初等阵；E(x)：x=y，令函数f(x1，x2，…，xl)=x1，x2，…，xl。

符号化为∀A((M(A)∧R(A))↔∃P1∃P2…∃

Pl(J(P1)∧J(P2)∧…∧J(Pl)∧E(A，f(P1，P2，…，Pl))))。

在个体域D内，应用线性代数中矩阵的初等变换很容易证得。公式的真值为1，因此公式是真命题。

函数符号与高等数学中的函数不同，主要体现在个体域与定义域上。个体域是个体名称集合，指量词的论域[6]，可以是世间万物，如下面的命题。

命题6 丽丽的哥哥是体操教练。

命题6翻译成谓词公式，涉及一元谓词和一元函数，其中“是体操教练”需引入谓词，“丽丽的哥哥”需引入函数。为此，取字头T表示“是体操教练”。令T(x)：x是体操教练，b(x)：x的哥哥，常项a：丽丽。符号化为T(b(a))。

这里个体域D是人类集合，公式T(b(a))具有真值，因为丽丽的哥哥可能是体操教练，也可能不是体操教练，只能选一。

可见个体域D可以是宇宙一切，而高等数学中的函数，其定义域只能是实数集合。由此函数符号与高等数学中的函数不同。

2.4 构造函数时易出现的问题

不考虑个体域，函数可能会产生错误，下面用两个例子加以说明。

命题7 设A，B是任意两个事件，则P(A∪B)=P(A)+P(B)-P(AB)。

将命题7翻译成谓词公式，涉及二元谓词和一元、二元、三元函数，其中“=”需引入谓词，涉及的运算需引入函数。为此，取字头E表示“=”。令E(x，y)：x=y；φ(t)：计算t的概率；f(x，y)=x∪y；g(x，y)=xy；h(x，y，z)=x+y-z。

符号化为∀A∀BE(φ(f(A，B))，h(φ(A)，φ(B)，φ(g(A，B)))。

此谓词符号化错误在于个体域发生了变化，量词约束的变量A，B是随机事件，因而个体域自然是所有随机事件组成的集合。而函数φ(t)的值域是[0，1]，前后不一致。与定义矛盾。

命题8 在xoy平面内，存在函数u(x，y)，使得du(x，y)=(x+2y)dx+(2x+y)dy。

将命题8翻译成谓词公式，涉及一元谓词和二元函数，其中“=”需引入谓词，“du(x，y)”“(x+2y)dx+(2x+y)dy”需引入函数。为此，取字头E表示“=”。令E(x，y)：x=y，f(t)=“计算t的全微分”，g(x，y)=(x+2y)dx+(2x+y)dy。

符号化为∀x∀y∃u(x，y)E(f(u(x，y))，g(x，y))。

此谓词符号化错误在于两个个体域，量词约束的变量x，y和u(x，y)分别是实数和二元函数，因而x，y的个体域自然是实数的集合，函数f(t)的个体域是二元函数的集合。一个谓词公式，解释在两个不同的个体域中，产生了矛盾。

3 结语

本文讨论了“离散数学”课程中谓词逻辑符号化时函数的应用，将一般命题在谓词逻辑中符号化是教学的难点。数学中很多概念、定理都不能死记硬背，只有学生对这些概念有更深刻的理解，才能抽象出谓词公式，而数理逻辑的学习能培养和训练学生的抽象思维能力和严格的逻辑推理能力。

[1] 耿素云，屈婉玲.离散数学[M].修订版.北京：高等教育出版社，2004：58.

[2] 张微.数理逻辑中谓词逻辑推理错误的分析[J].合肥学院学报：自然科学版，2012，22(4)：1-7.

[3] 王敏.数理逻辑中的命题符号化的几个值得注意的问题[J].科技信息，2010(9)：196.

[4] 刘云霞.数理逻辑翻译中的几个因素[J].天中学刊，2003(4)：24-25.

[5] 朱寿华.关于分析中的命题演算[J].扬州师院学报：自然科学版，1989，9(4)：13-18.

[6] 孙吉贵，杨凤杰，欧阳丹彤，等.离散数学[M].北京：高等教育出版社，2002：58.

(责任编校：夏玉玲)

The Application of Functions in the Symbolization of Predicate Logic

SUN Cui-xian

(Department of Basic Science Teaching， Tangshan University， Tangshan 063000， China)

Based on different object domains and some specific examples， the author of this paper discusses the introduction and operation of functions， and the difference between predicates and functions in the symbolization of predicate logic propositions， and illustrates the improper use of functions and its causes.

object domain； predicate logic； function；symbolization of propositions

孙翠先(1963-)，男，河北丰南人，教授，主要从事数理统计研究。

O141.1

A

1672-349X(2016)03-0006-03

10.16160/j.cnki.tsxyxb.2016.06.002