医疗统计周期性预测问题的比较研究
李望晨,于贞杰,王在翔,张利平
(潍坊医学院“健康山东”重大社会风险预测与治理协同创新中心,山东潍坊261053)
医疗统计周期性预测问题的比较研究
李望晨,于贞杰,王在翔,张利平
(潍坊医学院“健康山东”重大社会风险预测与治理协同创新中心,山东潍坊261053)
文章立足医疗统计领域周期性预测问题,以门诊人次为例进行建模方法比较,为类似研究提供方法参考。采用方式为:方式1:门诊人次季度数据由X11法时序分解后提取季节指数消除季节波动,用ARIMA法和抛物线拟合外推。方式2:周期差分提取季节信息,二阶差分提取长期趋势,直接用季节ARIMA法建模。季节波动和短期相关间交互影响不清,试用简单季节或乘积季节模型。得出结论:方式1对周期时序资料分解后,由组合方法依次直观反映;方式2直接用季节模型拟合预测,乘积季节模型性能并非有替代性,简单季节模型更优。算例为载体用几类方法比较研究,对于医院统计领域周期性预测问题有借鉴意义。
时间序列;组合模型;X11法;ARIMA;乘积季节模型
0 引言
医疗统计工作领域经常见时间序列预测问题,如传染病或慢性病发病数、发病率、门诊或住院人次、医疗营业收入、卫生费用支出等。这些事物受到社会、经济、环境等复杂因素的影响,对其解读分析也是卫生政策制定者、公共卫生干预者、卫生行政管理者关心的问题。
由于影响因素复杂性,传统回归模型结构模式确定、参数选择困难,指标难以量化。时序资料本身随时间延伸表现规律性,适合于时间序列分析。时间序列方法在数学、统计学、计量经济和信息科学推动下,理论体系和应用实现较为成熟[1,2],近年来在医疗卫生领域得到推广应用,如ARIMA法、曲线拟合法、灰色系统法、数据挖据技术,其中ARIMA法有代表性,对于随机时序资料拟合较好,对于趋势性、周期性特点资料也有很强适应性。医疗统计领域常见周期性数据资料[3](如门诊人次、收入、费用),多采集为月度或季度资料,观察期长、数据丰富、周期明显、长期平缓,这类事物规律性好于传染病疫情时序资料。对此有必要引入适当方法建立模型,借助算例实现为类似研究提供方法借鉴。
第一种方式,鉴于月度或季度周期变化时序资料周期性、趋势性较明显,可用时间序列分解法提取信息,X-11过程法可用于提取季节指数[4],趋势因素可用曲线拟合法或ARIMA法。时序分解后从两种视角建立拟合模型,外推预测及合并信息后再预测未来情况。第二种方式,传染病预测为当前热点问题,乘积ARIMA法对传染病月度数据表现应用代表性。对于季节性变化资料,首先用步长差分方法提取季节信息,低阶差分提取长期趋势信息,季节方法与ARIMA模型结合建模型,必要时比较简单季节模型与乘积季节模型研究效果。
1 对象资料
以医疗统计领域时序资料为立足点建立模型和进行实证研究,方法学视角下对于门诊或住院人次、医疗收入等周期性指标有普适借鉴意义。某二级甲等医院2004—2014年按季度统计门诊人次数据为例,以2004—2013年建立拟合模型,对2014年进行预测验证。门诊人次数据随季度变化呈周期波动,年度间有平缓增长特点,见表1和图1所示。
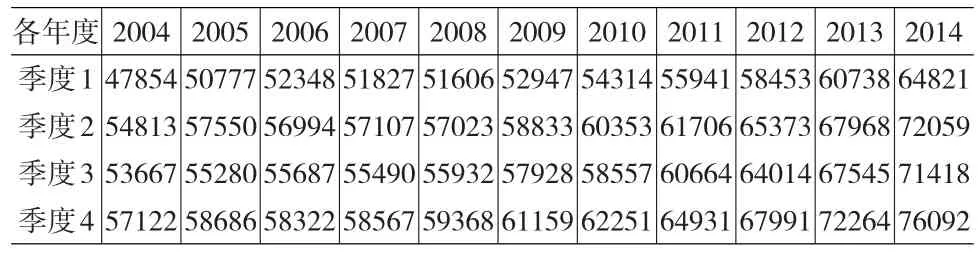
表1 某医院门诊人次数据
2 建模方式一
原始序列有明显趋势变化特点,对2004—2013年时序分解,提取季节指数后剩余序列有趋势增长及随机变化特点,用曲线拟合法或ARIMA法拟合趋势规律并外推预测未来[5],与季节指数相乘后还原为2014年情况。组合方法在SAS软件环境下计算实现方便。
2.1季节指数提取
由于门诊人次数据有明显季节变化特点,可经时间序列分解提取长期趋势、周期性季节指数、不规则变化部分等。X-11法由美国国情调查局建立,由于需要用到11次移动平均而得名,可据此对门诊人次数据提取季节指数: 92.882%、102.616%、99.544%、104.963%,消除季节因素后长期趋势见图2、剩余随机序列见图3所示。
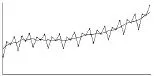
图1 原始数据
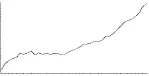
图2 长期趋势
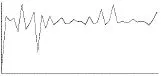
图3 不规则波动
2.2ARIMA法
ARIMA表达式Φ(B)▽dxt=Θ(B)εt,其中φi为自回归系数,θj为移动平均系数。Φ(B)=(1-φ1B-…-φpBp)为自回归多项式,Θ(B)=(1-θ1B-…-θqBq)为移动平均多项式, Bkxt=xt-k为k步延迟算子,▽d=(1-B)d为d阶差分算子。
根据数据资料确定模型结构、识别参数、检验模型显著性,否则要不断调整优化模型。趋势变化序列要经低阶差分后转化为平稳序列。由AIC、SBC最小准则选择最优模型,由最小二乘法识别参数。由残差纯随机性检验后,由模型进行短期外推预测。
正试期第2、第4周采用全粪收集方式采集粪样,每组用蛇皮袋固定于随机选取的4只试验羊尾后,每日更换两次并称重,将饲料样与粪样带回实验室进行常规分析计算养分表观消化率。正试期第2、第4周每组随机选取4只试验羊,晨饲后3 h利用负压原理经口腔采集瘤胃液各30 ml,四层纱布过滤后,采用上海雷磁pHS-3C型精密pH计立即测定pH值,之后将滤液分装在3个10 ml灭菌离心管中,置于-20℃下保存待测NH3-N浓度和MCP含量。
门诊人次序列消除季节指数,长期趋势序列用ARIMA法拟合。趋势序列经二阶差分消除趋势。在p,q≤6中自动寻优定阶,BIC(1,0)=11.757最小,认为AR(1)模型最合适,这也符合简化原则。条件最小二乘法识别参数,说明参数显著(P=0.0001),(1+0.57965B)(1-B)2xt=εt为表达式。经模型显著性检验,残差为纯随机序列,延迟阶数6,12,18,24时,P=0.7355,0.7495,0.8347,0.0672>0.05,模型对序列拟合显著有效。对2014年各季度趋势外推预测,得到70202,71347,72614,73810,由季节指数合并计算2014年门诊人次65205,73213,72283,77473,相对误差绝对值为0.59%,1.60%,1.21%,1.81%。
2.3曲线拟合法
门诊人次序列消除季节因素后有平稳长期趋势特点,可用曲线拟合法建立模型,如二次或三次抛物线、指数曲线、Logistic曲线等。经试选,本例适合三次抛物线反映趋势,对近期数据变化规律拟合更好,表达式为xt=52710+457×t-23.344×t2+0.555×t3。决定系数为R2=0.982,F检验P<0.001,模型拟合不错,对2014年各季度趋势外推预测,得到70424,71808,73286,74860,由季节指数合并计算2014年门诊人次65411,73687,72952,78576,相对误差绝对值为0.91%,2.26%,2.15%,3.26%。
门诊人次月度数据消除季节波动后,ARIMA法和趋势外推法均可用于建立模型。ARIMA法为随机时序方法,将历史序列和残差序列纳入线性模型。不易对事物规律直观解释,优点是拟合性能和短期预测精度高。趋势外推曲线能解释事物随时间变化规律,须有曲线变化特点,序列波动明显存在时不太适合。经计算比较,ARIMA效果优于多项式曲线。趋势拟合与外推效果比较见图4—图5,组合模型对原始序列拟合及外推效果见图6所示。

图4 ARIMA模型

图5 三次抛物线模型
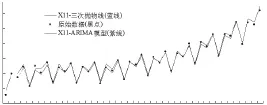
图6 三种组合模型拟合外推效果比较
3 建模方式二
考虑门诊人次数据随季度呈周期波动变化、随年度长期平缓趋势增长特点,借鉴当前传染病预测文献中常见季节ARIMA模型[6~7],用以建立拟合模型及外推预测。
3.1简单季节AR IMA模型
由于门诊人次序列不平稳,用周期步长差分消除季节波动,用低阶差分消除平缓增长趋势,将数据转化为平稳序列。模型结构如下:
门诊人次序列随季节周期波动、随年度有长期趋势,季节变化用4步差分,经一阶差分或二阶差分消除趋势特点,过度差分会损失信息,差分序列若平稳化则可以建立模型。经计算分析,以2阶差分消除趋势、以4步差分消除季节波动,经白噪声检验得知,延迟6阶时,P=0.1452>0.05,该序列可以建模分析。观察ACF、PACF是否落入两倍标准差内,调试阶数、确定结构和识别参数。模型结构以简单为原则,发现ACF一阶以后、PACF一阶及四阶时落入两倍标准差范围并继续拖尾,考虑低阶疏系数模型,模型ARIMA((4),1,1)表达式如下:
(1+0.38669B4)(1-B4)(1-B)2xt=(1+0.90475)εt。经延迟6,12,18,24阶时,P=0.4509,0.8271,0.9703,0.5971,说明残差为白噪声序列。对2014年门诊人次各季度外推预测,得到65127,72420,71452,76067;计算相对误差绝对值为0.47%,0.50%,0.05%,0.03%,预测效果非常好。
3.2乘积季节AR IMA模型
如果季节波动与长期趋势间有复杂交互影响,要用乘积季节ARIMA模型。该方法在传染病发病率、发病数预测中是当前热点,可能是传染病月度或季度资料特点决定的。对于本例门诊人次预测来说,简单季节模型经计算预测效果不错,可认为季节波动与短期相关间并无复杂关系,以下仍用乘积季节模型验证和进行比较。
以ARMA(p,q)提取短期相关性,以ARMA(P,Q)提取季节相关性。假设二者存在交互乘积关系,构造为乘积模型: ARIMA(p,d,q)×(P,D,Q)S:Φ(B)ΦS(B)▽D▽dxt=Θ(B)ΘS(B)εt;
其中Θ(B)=(1-θ1B-…-θqBq),
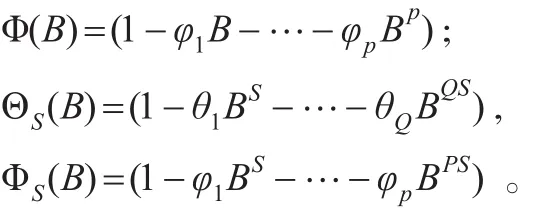
前面得知长期趋势用2阶差分,季度周期用四步差分。调试阶数及识别参数,模型结构ARIMA(1,2,0)×(1,1,0)4,表达式为(1-0.18884B)(1-0.32985B4)(1-B4)(1-B)2xt。=εt残差序列延迟6,12,18,24时,P=0.1178,0.5641,0.6726,0.1108>0.05,认为模型显著。对2014年门诊人次各季度外推预测,得到65061,72547,71978,76881,计算相对误差绝对值0.37%, 0.68%,0.78%,1.04%。然后根据ACF和PACF特点,继续选择可能模型结构如ARIMA(1,2,1)×(1,1,0)4,表达式为(1+0.40425B)(1-0.25856B)(1-B4)(1-B)2xt=(1+0.9655B)εt。延迟6,12,18,24时,残差序列P=0.1878,0.6384,0.7670,0.2152>0.05,认为模型显著。对2014年门诊人次各季度外推预测,得到64988,72311,71860,76605,计算相对误差绝对值0.25%, 0.35%,0.62%,0.67%。
乘积季节ARIMA模型预测精度稍微改善,又反复试取了多种模型结构,但相对简单季节ARIMA模型并未明显改善预测精度,认为季节波动和短期相关无交互关系,比较见图7所示。
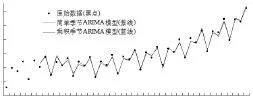
图7 两种季节模型拟合外推效果
以上从两种方式、四种模型对门诊人次季度数据进行预测。第一种方式:X11过程法与ARIMA、多项式曲线设计组合模型。第二种方式:假设季节波动和短期相关性是否有交互关系,构造简单季节ARIMA模型、乘积季节ARIMA模型。2004—2013年季度数据用于确定模型结构、识别参数,对2014年情况预测情况比较见表2所示。
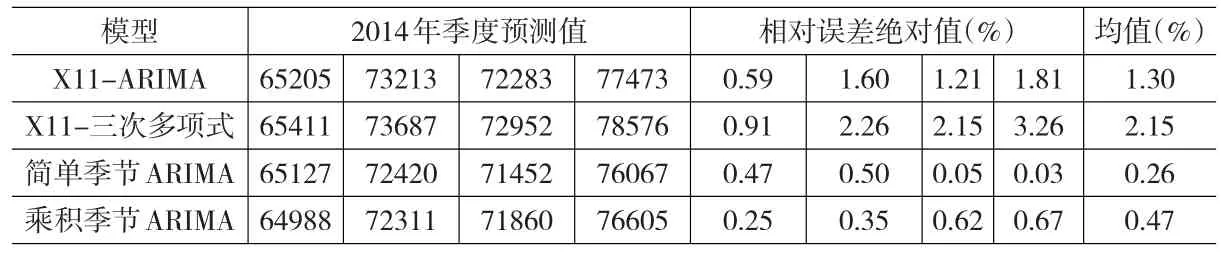
表2 模型预测精度比较
4 讨论
门诊、收入等医疗统计工作领域多数指标为例,月度、季度数据随时间变化往往有规律性。影响因素复杂而无法确定模型结构或识别参数,可以尝试由时序数据由时间序列分析方法建模,时序数据可分解为长期趋势、季节波动和随机无序部分,由数据资料计算季节指数,消除周期波动后分析长期趋势,也可直接应用季节ARIMA模型。
一种方式是,鉴于季节指数较明显,以X11法作为时间序列分解法提取信息,原始序列不再有季节波动特点,考虑这类序列有平滑且类似曲线变化特点,以某类曲线拟合时序规律,也可由ARIMA法直接建模。经外推预测后将预测值与季节指数合成未来预测值。另一种方式是,序列季节波动与长期趋势不给予分解提取,而是直接建立季节ARIMA模型,若季节波动与短期相关交互不明显则用简单季节模型,若交互影响存在则用乘积季节模型。
以某医院门诊人次预测为例,季度数据周期性变化有规律,历史数据中季节波动且平稳增长,观测期长、数据连贯、规律性强,明显有季节波动和平稳延续特点,后期增幅明显,长期较平缓且无转折因素影响。采用以上几种模型演示实施流程,为医疗统计工作提供方法借鉴。两种方式又分别给出两种算法,比较模型原理特点、拟合性能和预测精度。以2004—2013年数据拟合模型,预测2014年情况并与真实值计算相对误差,X11-ARIMA法1%左右,X11-三次多项式2%左右,简单季节ARIMA0.5%以下,乘积季节ARIMA0.5%左右。
第一种方式为组合建模方法,适用于季节指数较明确情况,消除季节波动以后的长期趋势规律,ARIMA法好于曲线拟合法。第二种方式直接用季节ARIMA模型,经算例验证表明季节ARIMA模型拟合性能、预测精度均好于第一种方式。预测领域多数文献表明,月度或季度数据基本上用乘积季节ARIMA模型,这种思路未必千篇一律,经本例验证,门诊人次数据中季节波动和短期相关性无交互影响,简单季节ARIMA模型甚至优于乘积季节ARIMA模型,具体资料情况下可以进行试选优化,以便改善模型对资料拟合及预测适应性。
[1]王燕.应用时间序列分析[M].北京:中国人民大学出版社,2012.
[2]徐国祥.统计预测与决策[M].上海:上海财经大学出版社,2012.
[3]耿娟.ARIMA模型在医院门诊量预测中的应用[J].中国卫生统计, 2014,31(8).
[4]申铜倩,刘文东,胡建利等.X11-ARIMA过程在痢疾疫情预测中的应用研究[J].中国卫生统计,2014,31(3).
[5]李望晨.基于增长特征法与ARIMA的人均卫生事业费趋势预测比较研究[J].中国卫生统计,2014,31(3).
[6]陆波,闵思韬,闵红星等.应用ARIMA模型预测麻疹发病率的可行性研究[J].中国卫生统计,2014,32(1).
[7]张爱红,周培,申铜倩等.乘积季节ARIMA模型在食源性疾病预测中的应用[J].中国卫生统计,2014,31(3).
(责任编辑/浩天)
C913.4
A
1002-6487(2016)19-0078-03
教育部人文社科基金资助项目(15YJCZH087;14YJAZH101;14YJA630098);山东自然科学基金资助项目(ZR2015HL101);山东统计科研项目(KT16230;KT16231)
李望晨(1980—),男,山东潍坊人,硕士,副教授,研究方向:卫生管理统计。于贞杰(1971—),女,山东潍坊人,博士,教授,研究方向:卫生事业管理。王在翔(1963—),男,山东潍坊人,硕士,教授,研究方向:卫生管理统计。(通讯作者)张利平(1980—),男,山东潍坊人,博士研究生,讲师,研究方向:职业卫生评价。

