基于Epsilon-Nash策略的动态武器-目标分配方法*

王邑，孙金标，华玉光，王继辉

（空军指挥学院，北京100097）

基于Epsilon-Nash策略的动态武器-目标分配方法*

王邑，孙金标，华玉光，王继辉

（空军指挥学院，北京100097）

在大型任务规划软件的作战单元任务分配中，搜索零和博弈问题的纳什均衡点是求解任务分配的一种有效的方法。然而，纳什均衡点在决策中并不一定总是存在且唯一，这造成了纳什均衡策略在实际使用时具有较大的局限。通过采用Epsilon-Nash策略克服这种局限，并将其应用于自主空战任务规划系统中，通过仿真实验，证实Epsilon-Nash策略具有近似于纳什策略的效果。

战术决策，武器-目标分配，Epsilon-Nash，博弈论

0 引言

动态武器-目标分配问题（Dynamic Weapon-Target Assignment，WTA）是战场指挥决策中的关键问题［1］。对该问题的求解，是很多武器任务规划软件的核心功能。

以博弈论为基础的作战指挥控制理论在战场指挥决策中得到了广泛的应用。在敌我双方具有一定情报信息理解的前提下，通过构造对策矩阵，寻找博弈均衡点，来搜寻作战收益最高的分配方案，是解决武器-目标分配问题的可行的方法。

博弈论中最常讨论研究的博弈均衡为纳什均衡（Nash Equilibirum），采用纳什均衡解决任务规划问题的时候，必须保证决策矩阵都有全局唯一的纳什均衡点。这种决策矩阵博弈对策中存在且唯一的纳什均衡点称之为纯纳什均衡点，而据文献［2］，大多数非零和博弈对策矩阵不存在纯纳什均衡点，因此，在实践中，必须考虑纳什均衡点非唯一或不存在的情形。在理论探讨中，通常采用混合策略（Mixed Strategy）［3］，简化决策矩阵［4］等方法来进行无纯纳什均衡点矩阵的决策。

影响纳什均衡策略在动态武器［6］-目标分配问题中的使用问题，除了纯纳什均衡点可能不存在这个理论问题之外，还有搜索纳什均衡点本身的效率问题。经过科学论证，搜索纳什均衡点、判断纯纳什均衡点数量的计算复杂度都是PPAD-Complete难度，而若对策矩阵中出现元素缺失或不确定的情况，随之产生的纳什均衡点非唯一或不存在使情况更加复杂，除此以外，搜索混合纳什均衡点、简化决策矩阵等工作涉及也都是PPAD-Complete难度的计算，因此，在实践中，基本上没有讨论战役规模决策矩阵的相关论述，而大多是围绕小规模2对2空战等简单对策中讨论纳什均衡的求解。

综上所述，若有方法能够克服纳什均衡点数量的问题，且能够快速有效地计算得到接近纳什均衡的结果，那将是非常实用的。

本文将Epsilon-Nash策略引入解决纯纳什均衡不存在时的局部最优化问题，使用经过线性时间就可计算出的Epsilon-Nash均衡点来代替纳什均衡点，得到纯纳什均衡的近似解，大大地提高了问题的求解效率，并拓宽了博弈论方法在WTA问题中的运用范围。通过蒙特卡洛仿真，与全信息最优策略，和无信息最优策略进行效用对比来分析方法的使用效果。通过实验表明，Epsilon-Nash策略能够接近于纯纳什均衡所产生的效能。

1 基于Epsilon-Nash的武器-目标分配

1.1WTA问题描述

设A，B方进行攻防对抗，A为红方，有N个单位，B为蓝方，有M个单位，则A={1，2，…，n}，B= {1，2，…，m}，设Pij表示A组第i单位攻击B组第j目标的击毁概率，对应的存活概率是qij=1-Pij，则目标j遭受多目标攻击后的存活概率为：

其中，xij为A组第i单位攻击B组第j目标的武器数。则xij的约束条件为：

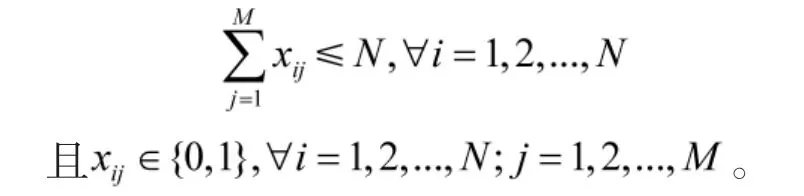
设红方为A，蓝方为B，行动规划共有K步。行动步骤为k=0，1，…，K，各步可用作战单位数为N（k），M（k），设在决策中每一步都有评价函数，红方为JA（x（k），y（k）），蓝方为JB（x（k），y（k）），其中：

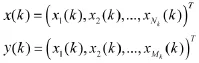
分别是NA（k），MB（k）维向量，表示红蓝双方每个作战单元第k步的目标分配策略。

设第k步时，红方第i作战单元打击蓝方第j作战单元的毁伤概率为，对应的蓝方第j作战单元打击红方第i作战单元的毁伤概率为，设分别是第k步起始时红方第i作战单元和蓝方第j作战单元的生存概率，则生存概率的计算式为：

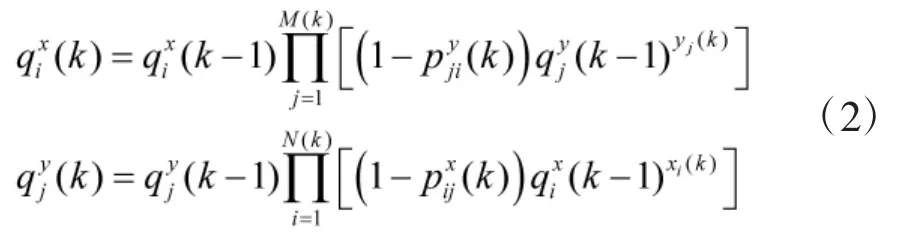
每个作战单元的价值不同，设Wx（i）表示红方第i个作战单元对红方的价值，Wy（i）表示该作战单元对蓝方的价值。设Wy（j）表示蓝方第j个作战单元对蓝方的价值，Wx（j）表示该单元对红方的价值。相应地，红蓝双方的策略评价函数可以写为：

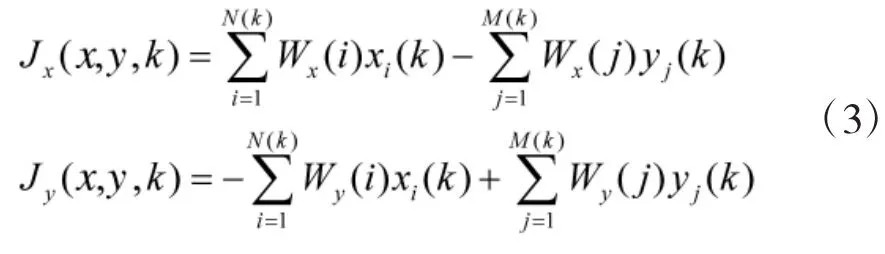
1.2WTA问题的Nash均衡解

设在评价函数JA下，对B方策略y，A方的最优策略x*，定义为：

对于B方给定的策略y，A方由最优策略x*变为其他策略x，造成的损失（又称悔值regret）为：

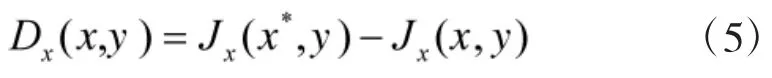
对称地，对A方策略x，B方由最优策略y*变为其他策略y，造成的损失为：

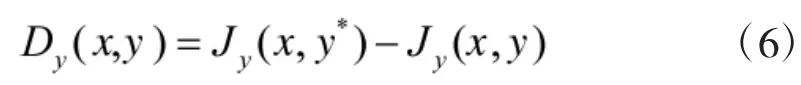
Dx（x，y），Dy（x，y）严格非负。

当Dx（x，y）=Dy（x，y）=0时，双方策略为纳什均衡策略对。

定义（WTA问题的纳什均衡策略）：

称uA，uB纳什策略对，当且仅当：

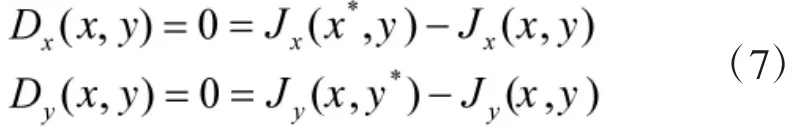
若定义双方的累积损失为：

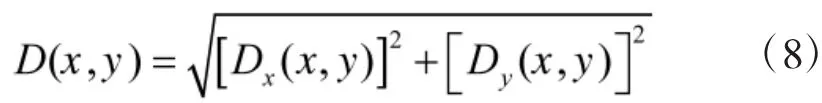
则，纳什策略对满足：

将式（7）～式（9）给出的纳什策略对条件带入式（3），得到许多步规划以下目标函数：

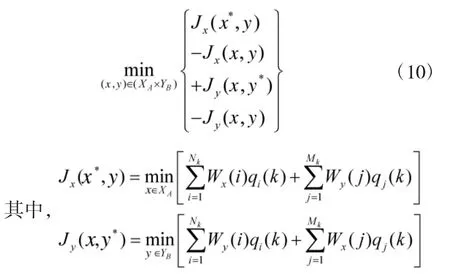
1.3一种Epsilon-Nash均衡策略

由于动态武器-目标分配问题的每一步都是NP难优化问题，故式（10）没有解析解，虽然可以对模型进行适当简化，使其符合双矩阵博弈的基本形式，但搜索其Nash均衡解的复杂度仍然是PPAD-Complete难度，且如前所述，纯纳什策略的存在性和唯一性无法保证，因此，需要引入Epsilon-Nash均衡策略作为纳什均衡策略的替代。

双矩阵博弈：

博弈空间G=（V，E）中，博弈方i∈V有mi个纯决策方案，j∈V有mj个纯决策方案，则：双矩阵博弈规模mi×mj，〈A（i×j），A（j×i）〉，对所有（i，j）∈E，i方的支付函数（即决策收益）为所有博弈分支付的总和：

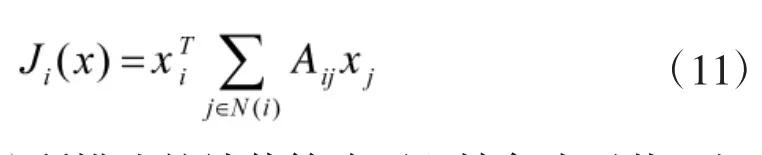
如式（8）所描述的纳什策略可以抽象为寻找双矩阵博弈问题的纳什均衡点，非合作非零和双矩阵博弈Γ=〈A，B〉，策略对（x*，y*）为纳什均衡，当且仅当，

①对行博弈方（row player）任意混合策略x，xTAy*≤x*TAy*且，

②对列博弈方（column player）任意混合策略y，x*TBy*≤x*TBy*，

定义（Epsilon-Nash策略）：

②对列博弈方（column player）任意混合策略y，，

引理［5］（（2+λ）/4-纳什均衡存在定理）：

一个n×m非负正规化非合作双矩阵对策Γ=〈A，B〉中，设为所有行（列）玩家所有纳什均衡决策中支付最小者，且设λ=max，则必存在线性时间可求得的（2+λ）/4-纳什均衡策略。

（2+λ）/4-纳什均衡求解方法：

设如下线性规划问题：

线性规划1：

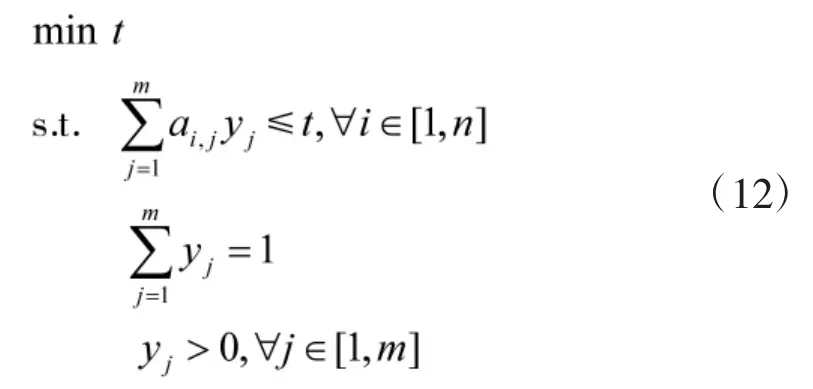
线性规划2：

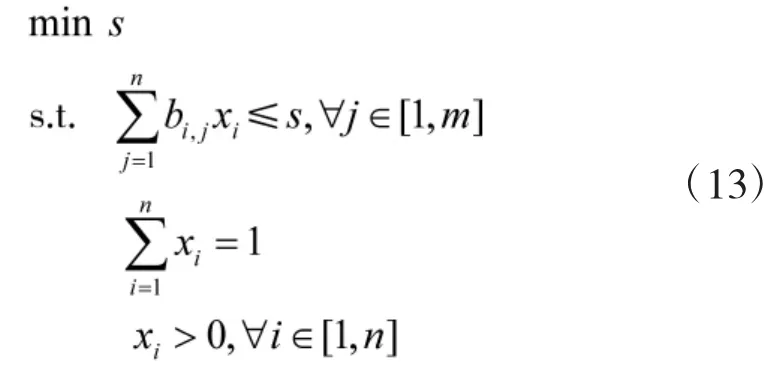
设t*，y*，s*，x*分别是线性规划1和2最优解，则存在至少一行r∈［1，n］，满足，一列c∈［1，m］使。即最优解的行号和列号分别是r，c。

1.4钟摆搜索Epsilon-Nash策略

由于对抗双方控制变量x（k），y（k）属于动态变化的量，所以多步预测是极复杂的问题。为简化计，可以用钟摆交替搜索法。首先假设蓝方两步的步骤是{y（k），y（k+1）}0，相应地算出对应的策略{x（k），x（k+1）}0，然后再根据此策略计算蓝方的响应策略{y（k），y（k+1）}1以此类推。结束终止条件为：

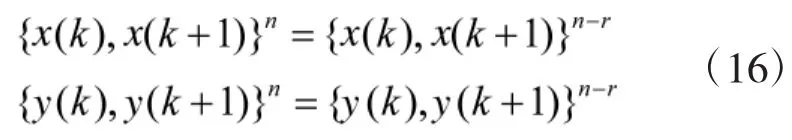
其中r≥1，当搜索结束，选取在其中满足线性规划式（12）、式（13）的量，即可构造Epsilon-Nash决策输出。

1.5Epsilon-Nash策略评价

为验证Epsilon-Nash策略目标分配方法的实际效果，定义两种其他策略作为参考策略。即，全信息最优策略和无信息最优策略。

定义（全信息最优策略）：

红方全信息最优策略{x*（k），x*（k+1）}∈XA*（k）为在给定蓝方作战单位y（k）条件下，在后推步长d=1时，满足如下不等式：

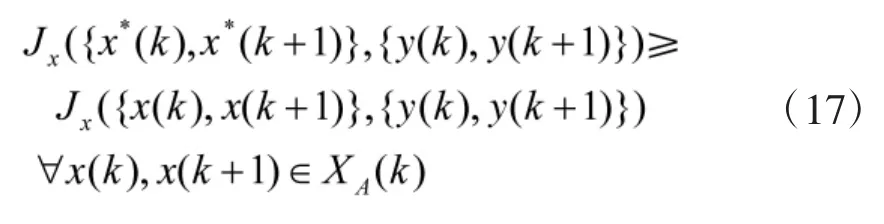
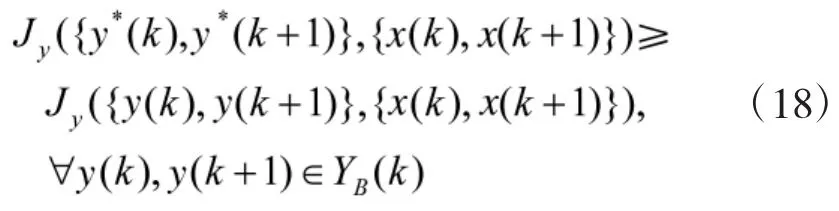
全信息最优策略是在完全知晓对方策略的前提下得到的，且仅知道当前时刻对方的策略，其策略的目标函数可以在下一个运算周期内进行推测。

定义（无信息最优策略）：

无信息最优策略x（ok），在k步骤时，，任一方的决策满足己方获益最大，即，蓝方以此类推。无信息最优策略即完全忽略对方策略而产生的一种策略。

2 实验验证

为验证Epsilon-Nash策略在动态武器-目标分配问题中的效用，进行了红蓝双方各10个目标的蒙特卡洛仿真。假设红蓝双方的作战单元价值相同，每次仿真生成新的随机决策矩阵，首先假定了两个16×16矩阵，分别是红方对蓝方以及蓝方对红方的杀伤概率，取值服从［0，0.5］区间上的正态分布。策略评价函数与式（3）相同，作战单元价值服从［0，1］区间上的正态分布，且对称构造，即。然后连续执行3轮攻击，即双方进行决策—攻击3次。统计3轮攻击后双方的存活作战单元价值总和，数值大者胜利，然后重置仿真参数，进入下一局。每种配置执行10 000局仿真。实验1中，红蓝方均采用Epsilon-Nash策略进行对抗；实验2中，红方采用Epsilon-Nash策略，蓝方采用全信息最优策略；实验3中，红方采用Epsilon策略，蓝方采用无信息最优策略。实验的评价指标为胜利率，即胜利局数占总局数的百分比，仿真的结果如表1所示：

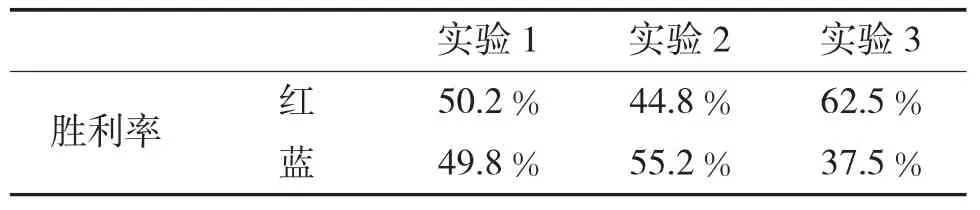
表1 仿真实验结果

从表1中可以看出，实验1的结果与实验2的结果更为近似，采用Epsilon-Nash策略的总体效果与敌方采用Epsilon-Nash的效果相同，优于无信息最优分配策略，低于全信息最优策略。实践中，当纳什均衡存在时，一方选择纳什均衡而另一方选择全信息最优策略，其结果应该与双方均选取纳什均衡策略结果一致，故，Epsilon-Nash策略在对抗全信息最优策略时，其效果为相当或略低于全信息最优策略。而Epsilon-Nash策略对抗无信息最优策略，则显现出较大的优势。这表明，Epsilon-Nash策略产生的结果非常近似于纳什策略，且比纳什策略的求解范围更大。

3 结论

本文采用了一种Epsilon-Nash策略来克服纳什均衡点不存在或不唯一时的动态武器-目标规划问题，采用蒙特卡洛法和随机矩阵，通过实验验证了Epsilon-Nash策略相对全信息和无信息最优策略的效能。通过试验表明了Epsilon-Nash策略近似于纳什策略，可作为无全局纳什点动态武器-目标分配问题的解法策略。

［1］刘传波，邱志明，吴玲，等.动态武器目标分配问题的研究现状与展望［J］.电光与控制，2010，17（11）：43-48.

［2］BRANDT F，FISCHER F，HOLZER M.Symmetries and the complexity of pure Nash equilibrium［J］.Journal of Computer and System Sciences，2009，75（3）：163-177.

［3］RENY P J.On the existence of pure and mixed strategy Nash equilibriaindiscontinuousgames［J］.Econometrica，1999，67（5）：1029-1056.

［4］KNUTH D E，PAPADIMITRIOU C H，TSITSIKLIS J N.A note on strategy elimination in bimatrix games［J］.Operations Research Letters，1988，7（3）：103-107.

［5］KONTOGIANNIS S C，PANAGOPOULOU P N，SPIRAKIS P G.Polynomial algorithms for approximating nash equilibria of bimatrix games［M］.Berlin：Springer Berlin Heidelberg，2006：286-296.

［6］周全，刘娟.基于动态武器目标分配的建模［J］.四川兵工学报，2010，31（9）：14-15.

Research of Dynamic Weapon-Target Assignment Problem Based on Epsilon-Nash Equlibirum

WANG Yi，SUN Jin-biao，HUA Yu-guang，WANG Ji-hui
（Air Force Command College，Beijing 100097，China）

In large scale mission planning software，the mission assignment of asset can be effctive when searching nash equilibria in non-cooperative non zero sum game problem.However，the pure nash equlibrium is not always exist and single，in which case limit the use of nash strategy in Weapon-Target assignment.A Epsilon-Nash Equlibirum method to overcome the limitation is proposed.Apply it in a air combat mission planning system，through simulation test，the epsilon-nash strategy can be as effective as pure nash strategy.

tactical decision，weapon-target assignment，epsilon-nash，game theory

TP391.9

A

1002-0640（2016）11-0012-04

2015-10-12

2015-11-17

航空科学基金资助项目（20131789004）

王邑（1984-），男，四川成都人，博士，工程师。研究方向：计算智能、空军合同战术模拟。