基于直觉模糊时间Petri网的不确定性时间推理方法*

任神河，郑寇全，雷英杰，王睿

（1.咸阳师范学院，陕西咸阳712000；2.西安通信学院，西安710106；3.空军工程大学防空反导学院，西安710051）

基于直觉模糊时间Petri网的不确定性时间推理方法*

任神河1，郑寇全2，雷英杰3，王睿3

（1.咸阳师范学院，陕西咸阳712000；2.西安通信学院，西安710106；3.空军工程大学防空反导学院，西安710051）

针对Petri网模型在对复杂不确定性时间信息描述和推理方面的局限性，在定义直觉模糊时间函数以及网络变迁约减规则的基础上，融合直觉模糊时序逻辑（IFTL）、直觉模糊Petri网（IFPN）以及线性逻辑推理的理论优势，构建了直觉模糊时间Petri网（IFTPN）推理模型，并提出了基于IFTPN的不确定性时间推理算法，较好地解决了态势评估中冲突事件间的不确定性时间推理问题。最后，通过典型的战场想定验证了该时间推理方法的有效性和优越性。

直觉模糊集，Petri网，时序逻辑，时间推理

0 引言

由于系统的随机性、缺乏属性参数以及信息不完备等因素的影响，战场态势在时间信息方面存在较大的模糊不确定性，而这类时间知识的描述与推理是整个态势评估系统建模需要研究和解决的关键问题，也是其智能化的集中体现［1-3］。直觉模糊Petri网（Intuitionistic Fuzzy Petri Net，IFPN）将直觉模糊集（Intuitionistic Fuzzy Set，IFS）与Petri网推理理论相融合，利用直觉模糊函数描述网络库所及其变迁参数，通过直觉模糊逻辑运算进行网络并行推理，提高了模型推理的精度与可靠性，为不确定性问题的建模与求解提供了新的思路和方法［4-5］。然而，IFPN本身不具备时间语义，无法有效表征模型推理中不确定性事件发生的时间及其时态限制信息，模型适用范围有限。文献［6-8］通过遍历Petri网和计算时间模糊集函数进行不确定性时间推理，构建了模糊时间Petri网（Fuzzy Time Petri Net，FTPN）模型，增强了系统对不确定性时间知识的描述与推理功效。但是，FTPN难以定量分析和解决时间并发与冲突关系的信息处理以及模糊时延推理问题，模型无法适用于复杂不确定性的实时系统建模［9］。文献［10］定义了直觉模糊不确定时间区间与时间间隔，构造了未知时刻的直觉模糊时序逻辑（Intuitionistic Fuzzy Temporal Logic，IFTL）预测模型，提出了基于IFTL的不确定时间推理方法，扩展了时间推理对不精确、不完备等粗糙信息的处理功效，但该方法无法进行网络冲突事件间的不确定性时间推理。文献［9］利用IFS表征不确定性时间信息，初步构造了直觉模糊时间Petri网（Intuitionistic Fuzzy Time Petri Net，IFTPN）模型，并给出了线性时间推理方法，提高了模糊时延预测的准确性，但文献没有深入研究模糊时间函数的直觉模糊化方法，未将直觉模糊逻辑推理引入模型构建与网络变迁约减，算法复杂度高，推理精度难以满足战场态势评估的实际需求。

鉴于此，本文在定义带有直觉模糊可能性度量的直觉模糊时间函数（Intuitionistic Fuzzy Time Function，IFTF）及其运算方法的基础上，规范了IFTPN的相关概念，利用IFTL定义网络变迁约减规则，提出了基于IFTPN的不确定性时间推理算法，并应用于战场态势评估领域，有效地提高了Petri网模型对复杂不确定性时间信息分析与处理的精度和效率。

1 直觉模糊时间函数及IFTPN推理模型

IFTF是对模糊时间函数进行直觉模糊化拓展，其函数值表示不确定事件发生的直觉模糊时间及其呈现出的直觉模糊可能性度量［11］。因此，本文基于IFTL定义IFTPN中带有直觉模糊可能性度量的IFTF及其运算方法，并构建不确定性时间信息推理模型。

1.1直觉模糊时间函数

定义1（直觉模糊触发区间）假设网络变迁开始时刻落在时间区间上，结束时刻落在上，则直觉模糊触发区间SIF可定义为：

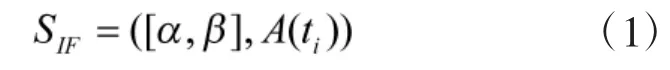
由此可见，定义1中，如果没有网络变迁与其发生冲突，则A（ti）=〈0，1〉；否则，A（ti）对应一个从时间区间［α，β］到实数区间集合［0，1］×［0，1］上的映射函数。若IFTPN中有多个网络变迁构成结构冲突，则可根据需求为每个变迁实时分配相应的直觉模糊触发区间，从而使得冲突中的网络变迁具有不同的触发可能性和优先级。同时，由于非隶属度的作用，直觉模糊触发区间相对模糊时间区间具有更强的不确定性描述能力，配合IFTF的计算能够更加准确地对模糊不精确时间信息进行定量表达与定性推理。

定义2（直觉模糊时间片）假设不确定时刻i落在时间区间上，且网络托肯在i到达库所的直觉模糊可能性为B（i），则直觉模糊时间片πIF（i）可定义为：

分别为区间1，2上的直觉模糊集，则可根据直觉模糊关系运算规则［12］定义直觉模糊时间片的合成运算为：

①“加和”直觉模糊时间片（additive date），即，则：

定义3（直觉模糊使能时间）直觉模糊使能时间是指网络变迁所需的所有资源（托肯）到达输入库所最迟时间对应的直觉模糊时间片。假设网络变迁t被n个托肯使能，其对应的直觉模糊时间片分别为，则根据式（5）定义直觉模糊使能时间e（）为：

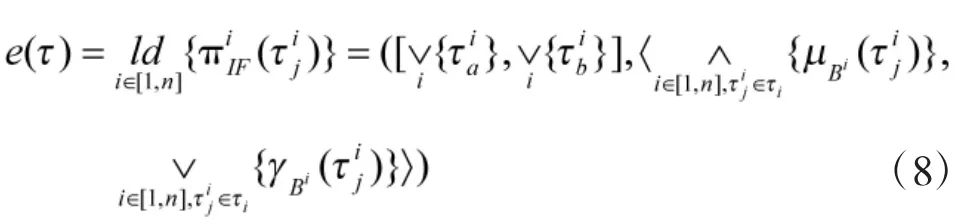
定义4（直觉模糊发生时间）直觉模糊发生时间是指直觉模糊使能时间的“较早”运算，用于描述不确定事件发生时间的直觉模糊可能性分布。假设多个使能事件对应的直觉模糊使能时间分别为，则其对应的使能事件ej的直觉模糊发生时间表示区间上的直觉模糊集；1、2分别为相对于变迁使能的相对时间，且当时，变迁t为瞬时变迁。

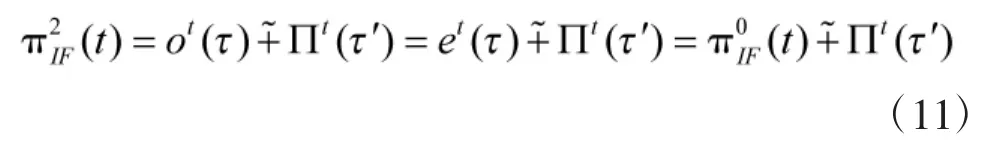
由此可见，网络输出库所托肯的直觉模糊时间片就等于输入库所托肯直觉模糊时间片与直觉模可表示为：

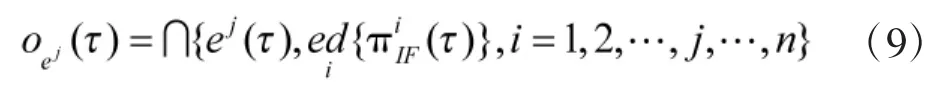
定义5（直觉模糊延迟时间）直觉模糊延迟时间是与网络变迁t输出弧相关的直觉模糊时间函数，可表示为：

1.2直觉模糊时间Petri网模型

基于TFTL对FTPN进行直觉模糊拓展，构建式（12）所描述的八元组IFTPN模型：

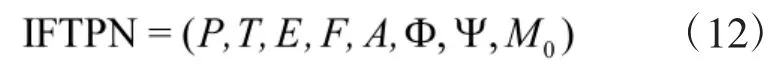
由此可见，IFTPN主要是利用IFTF对网络库所托肯值及其变迁使能过程进行描述，并将时间函数运算转换为区间数和直觉模糊集的交、并及关系运算，从而使得模型推理更加简单高效，符合不确定性时间推理的客观实际。

2 基于IFTPN的不确定性时间推理算法

传统的时间Petri网以及FTPN模型对不确定性时间信息的描述和处理均存在理论不足，无法准确反映网络变迁间并发和冲突时间逻辑关系及其使能运算过程［9］。而线性逻辑具有良好的可扩展性和时间逻辑描述性能，且能较好地与Petri网模型推理相融合，从而提升模型的逻辑表述与推导性能［13］。因此，本节对线性逻辑运算进行直觉模糊拓展，基于IFTL理论定义IFTPN的网络变迁约减规则，并给出不确定性时间推理算法。

2.1直觉模糊线性逻辑运算

IFTPN模型的线性逻辑主要是描述网络变迁触发的相关关系，其逻辑运算可定义为：

由此可见，若利用IFTL理论对IFTPN模型推理元素进行描述，其网络当前标识可表示为：，其中pk表示网络库所，mk为库所中的托肯数目；变迁ti的网络输入库所与输出库库所间的因果依赖关系可表示为：，其中表示变迁使能的直觉模糊时间片。

2.2IFTPN的变迁约减规则

假设α（pi），e（ti），o（ti）分别表示网络库所pi标识到达时间，变迁的直觉模糊使能和发生时间，则可定义IFTPN的网络变迁约减规则为：

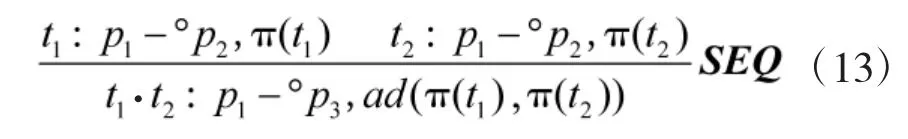
其中，“·”为变迁顺序触发连接符。

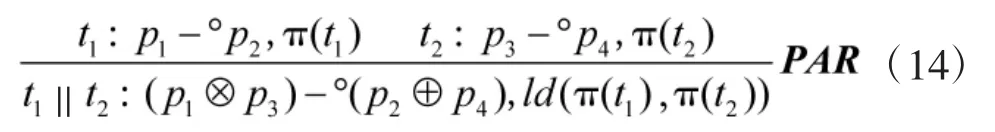
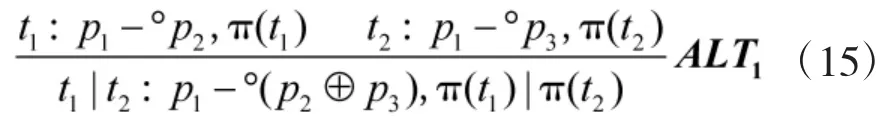
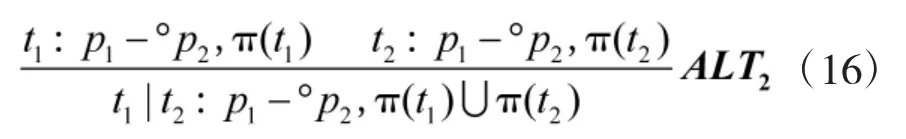
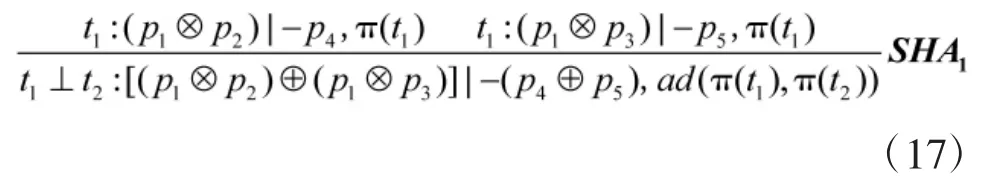
特别地，若p4=p5，则t1，t2也称变迁资源共享冲突关系，满足SHA2规则：

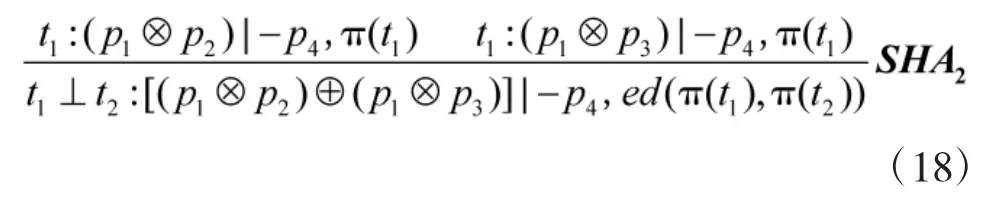
2.3基于IFTPN的不确定性时间推理算法

基于IFTPN的不确定性时间推理算法是将线性逻辑、IFTPN模型和直觉模糊时序逻辑理论相融合给出的不确定性时间信息定量描述与定性推理的方法，其算法步骤可描述为：

输入：问题相关变量（网络库所和变迁集合P，T，网络节点有向弧集合A，初始库所直觉模糊时间片πIF（ti）以及直觉模糊延迟时间∏IF（ti））。

输出：输出库所的直觉模糊时间片πIF（ti）。

Step1：根据问题描述，构建IFTPN模型；

Step2：如果IFTPN模型的起始与终止库所唯一，则转至Step3；否则，根据定义5，加入瞬时变迁，实现网络起始与终止库所唯一化，消除网络环路；

Step3：在IFTPN模型中查找问题事件所对应的网络库所；

Step4：根据式（13）～式（18）对IFTPN模型进行约减，获取最优化推理模型；

Step5：利用直觉模糊时间运算方法对最优化模型进行推理计算，获取输出库所对应的直觉模糊时间函数值；

Step6：研究分析网络推理结果，给出问题结论。

可见，若网络模型输入库所集维数为n，基于IFTPN的不确定性时间推理算法的时间复杂度为O（n）。

3 实例分析

为了验证算法的有效性，本文模拟带有冲突资源的空中作战态势评估想定，建立IFTPN模型，并进行不确定性时间推理。

3.1问题描述

如下页图1所示，假设空中预警作战指挥决策系统由预警雷达、预警机信息融合中心和战斗机群构成，则指挥决策过程可表述为：当预警雷达p1发现敌情后，将战场信息实时传输给预警机p3和距离敌机最近的两个战斗机群p2，p4，预警机和机群分别获取各自空域内的战场态势评估信息p6，p5，p7；同时，机群将态势评估上报给预警机信息融合中心并通过信息处理获取各自的威胁评估p9，p10。预警机综合自身态势和各机群上报信息，通过数据融合，形成战场综合态势评估p8，并以此为基础判明敌情，形成火力分配方案p11，以命令形式下达给各战斗机群。战斗机群根据各自的态势估计、威胁评估和对上级命令的理解结果p12，p13，形成自身范围内的火力分配方案p14，p15，并指挥战斗机进行攻击p16。因此，若假设网络初始标识p1的起始时间为0，则可根据网络变迁的具体含义和直觉模糊时间函数，为相应的网络变迁设定时间信息。由于t1表示雷达传送实时敌情信息，可设定为瞬时变迁，其他变迁的直觉模糊时间信息可依次表示为：

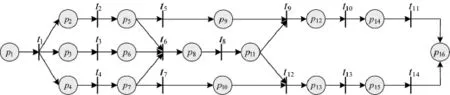
图1 空中作战态势评估系统的IFTPN模型

①t3、t2和t4分别表示预警机和战斗机群分别对各自战场态势进行评估，根据定义2，设

⑦t11和t14分别表示战斗机进行攻击，设定为瞬时变迁。

3.2基于IFTPN的不确定性时间推理

根据本文算法，利用网络变迁约减规则，对图1所描述的IFTPN模型进行约减，推理计算网络终止库所p16对应的直觉模糊时间函数。

①由于初始标识p1的起始时间为o，则网络库所标识p5，p6，p7对应的直觉模糊时间函数分别为：

③t9，t12为变迁资源共享冲突关系，根据式（20）可知：

④t10，t11与t13，t14分别为变迁顺序触发关系，且相互构成变迁并行触发关系，则根据式（13）、式（14）可知：

由此可见，网络终止库所p16在时间区间［18，22］到达的直觉模糊可能性最大，即从预警雷达发现敌情到战斗机开始攻击，最可能需要18～22个时间单位。同样，若设定直觉模糊可能性分布双重阈值，便可推理计算可能的时间区间，例如取双重阈值（0.8，0.2），利用直觉模糊截运算可获取时间区间为［17，23］，即从发现敌情到开始攻击最可能需要17～23个时间单位。而时间Petri网不能描述网络变迁的不确定性时间信息，FTPN无法处理网络变迁冲突推理问题。因此，IFTPN推理模型通过将时间推理方法拓展到直觉模糊领域，充分利用了直觉模糊集处理不确定时间信息的理论优势，将网络推理转化为直觉模糊关系运算，降低了系统复杂度，不仅提高了系统时间预测的准确性，而且给出了相应时间区间的可能性分布，从而使得推理结果更加符合不确定性态势评估的实际。

4 结论

本文通过定义IFPN网络推理IFTF及其变迁约减规则，融合IFTL、IFPN以及线性逻辑推理的理论优势，构建了直觉模糊时间Petri网推理模型，并给出了其不确定性时间推理算法，不仅解决了经典及模糊时间Petri网模型无法有效描述和处理复杂不确定性时间信息的理论缺陷，改善了Petri网模型对冲突事件中不确定性时间信息的处理功效，而且简化了模型及其推理过程，扩展了直觉模糊Petri网模型的实际应用范围，使其不论在专家系统还是指挥控制决策等领域均有很好的应用前景。如何进一步拓展IFTPN模型的应用范围，提高不确定性时间推理算法的鲁棒性能将是下一步研究的重点。

［1］王晓帆.信息融合中的态势评估技术研究［D］.西安：西安电子科技大学，2012.

［2］郑寇全，雷英杰，王睿，等.基于IFTBN的不确定性时间推理方法［J］.系统工程与电子技术，2014，46（10）：1994-1999.

［3］王晓帆，王宝树.基于贝叶斯网络和直觉模糊推理的态势估计方法［J］.系统工程与电子技术，2009，31（11）：2742-2746.

［4］郑寇全，雷英杰，王睿，等.基于BP算法的IFPN参数优化方法［J］.控制与决策，2013，28（12）：1779-1785.

［5］周创明，申晓勇，雷英杰.基于直觉模糊Petri网的敌意图识别方法研究［J］.计算机应用，2009，37（9）：2464-2467.

［6］RIBARIC S，HRKAC T.A model of fuzzy spatio-temporal knowledge representation and reasoning based on high-level Petri nets［J］.Information Systems，2012，37（3）：238-256.

［7］HSIEH F S，LIN J B.Temporal reasoning in multi-agent workflow systems based on formal models［J］.Lecture Notes in Computer Science，2012，7196（1）：33-42.

［8］江式伟，吕卫民，冯浩源.基于时间Petri网的装备体系可靠性建模与仿真［J］.系统工程与电子技术，2013，35（4）：896-899.

［9］申晓勇，雷英杰，华继学，等.基于IFTPN的不确定时间知识描述和推理方法［J］.控制与决策，2010，25（10）：1457-1462.

［10］郑寇全，雷英杰，王睿，等.基于IFTL的不确定时间推理方法［J］.控制与决策，2013，28（7）：1002-1006，1012.

［11］申晓勇，雷英杰，周创明，等.基于直觉模糊集的不确定时序逻辑模型［J］.计算机科学，2010，37（5）：187-189，273.

［12］雷英杰，王宝树，苗启广.直觉模糊关系及其合成运算［J］.系统工程理论与实践，2005，25（2）：113-118，133.

［13］刘婷，林闯，刘卫东.基于时间Petri网的工作流系统模型的线性推理［J］.电子学报，2002，30（2）：245-248.

Method of Uncertain Temporal Reasoning Based on Intuitionistic Fuzzy Time Petri Net

REN Shen-he1，ZHENG Kou-quan2，LEI Ying-jie3，WANG Rui3
（1.Xianyang Normal University，Xianyang 712000，China；2.Xi’an Communication Institue，Xi’an 710106，China；3.Air Defense and Antimissile Institute，Air Force Engineering University，Xi’an 710051，China）

To the limitation of the Petri net in the description and the reasoning for complicated and uncertain temporal knowledge，the intuitionistic fuzzy time function and reduction rules between the changes of Net are defined.Meanwhile，the theoretical advantages of intuitionistic fuzzy temporal logic（IFTL），intuitionistic fuzzy petri net（IFPN）and linear logic reasoning are fused，and the intuitionistic fuzzy time Petri net（IFTPN）model and reasoning method of uncertain temporal reasoning based on IFTPN are proposed.In so doing，the uncertain temporal reasoning matter in conflicts is solved better. Finally，the typical hypothesized battle environment validate the presented approach’s efficiency and its preference.

intuitionistic fuzzy set，petri net，temporal logic，temporal reasoning

TP18

A

1002-0640（2016）11-0030-06

2015-10-05

2015-11-07

国家自然科学基金（61272011，61309022）；国家重点实验室基金（2012ADL-DW0301）；陕西省自然科学青年基金资助项目（2013JQ8031）

任神河（1986-），男，陕西安康人，硕士研究生。研究方向：智能信息融合。