基于模糊群决策方法的铁路物流中心方案评价研究

毛根旺

MAO Gen-wang

（兰州铁道设计院有限公司 线路运输所，甘肃 兰州 730000）

(Transport Block Post， Lanzhou Railway Survey and Design Institute Co.， Ltd.， Lanzhou 730000， Gansu， China)

基于模糊群决策方法的铁路物流中心方案评价研究

毛根旺

MAO Gen-wang

（兰州铁道设计院有限公司 线路运输所，甘肃 兰州 730000）

(Transport Block Post， Lanzhou Railway Survey and Design Institute Co.， Ltd.， Lanzhou 730000， Gansu， China)

在阐述兰州新区铁路物流中心评价指标体系构建的基础上，针对 6 个备选方案，从总指标层、分指标层、分项指标层方面构建 3 级方案评价指标体系，运用改进的层次分析法确定各指标权重，计算隶属度，利用带权欧几里得贴近度对单决策组方案进行排序，采用相对熵集结模型求解群组最优决策方案。以兰州新区铁路物流中心多方案评价为实例进行分析，结果表明应用效果较好。

铁路物流中心；层次分析法；模糊群决策；方案评价

根据《铁路物流基地布局规划及 2015—2017 年建设规划》(铁总计统 [2015] 232 号)，将建设一级、二级铁路物流基地共 208 个[1]，建成后的铁路物流基地将成为集运输、装卸、仓储、配送、加工、信息等一体的现代化铁路物流基础设施，对提升铁路物流服务水平、增加铁路运量具有重要作用。但是，铁路建设资金筹措渠道较为单一，铁路投资重点多集中于新建铁路，用于既有场站设备设施更新改造和提高技术装备水平的投资比较匮乏[2]。因此，充分发挥建设资金的最大效益，需要对铁路物流中心的建设方案进行科学比选，优先选择综合效益最大的方案，避免主观决策造成物流设施设备闲置。通过采用模糊群决策方法，利用改进的层次分析法(AHP) 确定各指标权重，结合带权欧几里德贴近度对各方案进行排序，选出综合效益最优方案，最后引入相对熵模型解决公私合营模式 (PPP) 等多决策组产生的群决策问题。

1　铁路物流中心方案评价指标体系的构建

根据铁总计统 [2015] 232 号文件，兰州铁路局将在范围内建设东川铁路物流中心 1 个一级物流基地和银川南、镇罗堡、平罗、兰州新区、天水、圆墩、嘉峪关、平凉南、张掖、金昌共 10 个二级物流基地，以二级物流基地——兰州新区铁路物流中心各方案的比选为例进行研究。兰州新区铁路物流中心决策方案集 T 有 6 个备选方案 T = {t1，t2，t3，t4，t5，t6}[3]，如表 1 所示。

表1　兰州新区铁路物流中心比选方案概况

不同方案的接轨条件、工程难易度、交通条件、吸引运量大小、总投资及经济效益均有所不同。因此，需要对各因素进行归类，筛选出影响兰州新区铁路物流中心方案建设最主要的因素作为评价指标，建立兰州新区铁路物流中心方案评价指标体系。该方案评价指标体系主要分为 3 级：一级为总指标，二级分为社会因素、技术因素、经济因素 3 个指标，三级为相应的 14 个分项指标，如表 2 所示[4]。

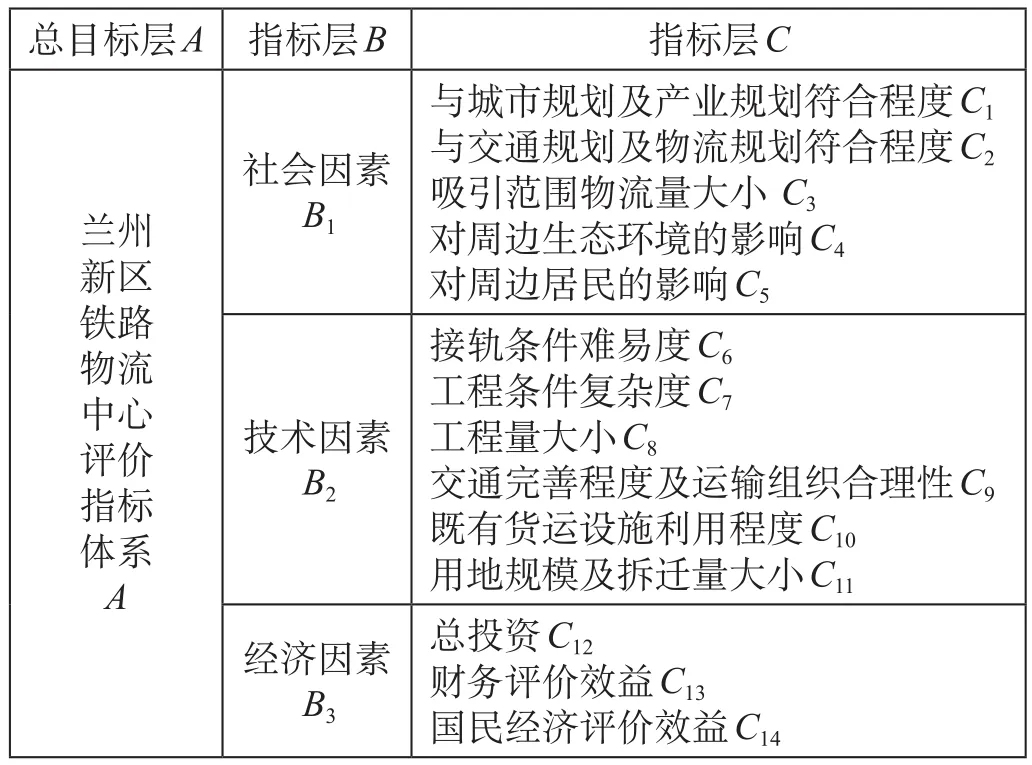
表2　兰州新区铁路物流中心方案评价指标体系

2　铁路物流中心方案评价方法

铁路物流中心方案评价方法主要有层次分析法、模糊综合评价法、数据包络分析法等，数据包络分析法多用于经济和管理效率的评价，对工程多方案评价具有一定局限性，因而考虑采用操作性强、应用广泛的层析分析法和模糊综合评价法进行评价，在结合二者优点的基础上再适当改进。首先，对 AHP 法进行改进，采用三标度法两两评价得出判断矩阵，并且转化为模糊一致矩阵，进而得到各指标的权重，在避免多标度主观判断弊端的同时，省去调整矩阵一致性的步骤；其次，利用带权欧几里德贴近度法将指标的特征值矩阵转化为最优贴近度向量，实现个体对评价方案的优排序；最后采用相对熵模型集结个体偏好得到群决策最终评价值，利用相对熵模型的良好集结性提高最终决策方案的可信度，实现客观、科学的综合评价目的。

2.1确定各指标权重

（1）根据模糊优先矩阵 A 建立模糊一致矩阵F。通过专家评估打分，采用三标度法得出相应的比较矩阵如下。

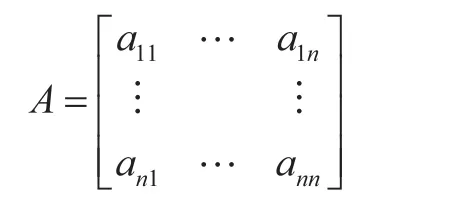
其中，aij为第 i 个指标对第 j 个指标的重要性，并且有 aii= 0.5，i = 1，2，…，n；j = 1，2，…，n。模糊一致矩阵 F 的元素，其中。

2.2根据特征值矩阵计算隶属度

如果有 s 个决策组，n 个比选方案，以 m 个指标进行方案比选评价，表示第 k 个决策组对第 j个方案第 i 个指标的评价值，得到相应特征值的矩阵计算公式为

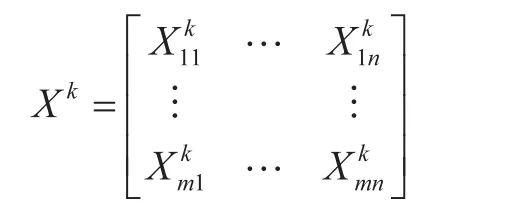
式中：i = 1，2，…，m；j = 1，2，…，n；k = 1，2，…，s。

对特征值矩阵中指标值有越大越优型和越小越优型 2 种，需要统一化处理，然后将特征值矩阵转换为隶属度矩阵 Rk。

2.3决策组最优决策过程

根据最大隶属度原理，模糊关系矩阵可以建立优等方案 Gk如下。

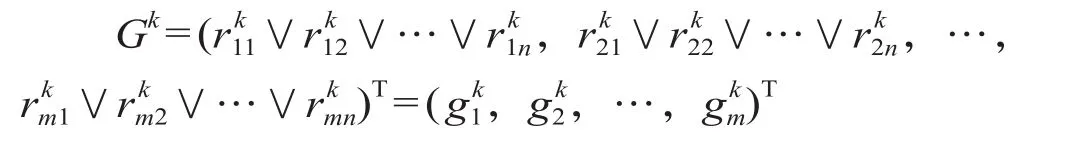
式中：∨为取大运算。

贴近度一般用来表示模糊子集之间的相近程度，取值在 [0，1] 之间，贴近度越大，表示 2 个模糊子集越相似；反之，相似程度越小。当贴进度概念拓展为带权贴进度，可以表示比选方案与优等方案 Gk的贴近程度。假设 m 个指标的权重为，带权欧几里德贴近度向量定义为 N (Rk，Gk) = 1－。其中， j = 1，2，…，n；k = 1，2，…，s。记 N (Rk， Gk) = Nkj，j = 1，2，…，n；k = 1，2，…，s。计算出 Rk与 Gk的带权贴近度，按照带权贴近度的大小排序得出 Nkj的优排列，带权贴近度最大者对应的方案为最优方案[6]。

2.4相对熵集结模型求解群组最优决策

实际决策问题更加复杂，通常由多个意见不同的决策组共同决定评价结果。每个决策组对方案的排序由其带权贴近度决定，具体反映决策组对方案的偏好程度。如果每个决策组的偏好反映为群偏好，并且反映到决策中，即可以找到群组最优方案[7]。

设决策方案集合为 A = {aj，j = 1，2，…，n}，决策群体的集合为 E = {ek，k = 1，2，…，s}，决策者权重集合为 W = {ωk，k = 1，2，…，s}，其中 ωk对应于第 k 个决策者的权重。对于 ∀ek∈ E，给出映射 πk：aj→xkj，xkj为决策者 ek对方案 aj的评价值。π：aj→ω*j为群偏好的映射。W*= (ω★1，ω★2，…，ω★n)T为群偏好向量。相对熵集结模型 P 计算公式为

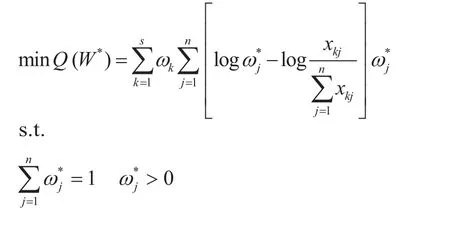
其中，P 的非线性规划解集是凸集，目标函数Q (W*) 是凸函数，属于凸规划问题，P 的局部最优解即为其全局最优解[8]。

3　案例分析

3.1各指标权重的确定

以兰州新区铁路物流中心评价其中一个决策组B1作为算例。

（1）首先选取方案评价指标 B1层次社会因素中的 C1，C2，C3，C4，C55 个指标为例，计算相关权重。在三标度体系中，aij= 1 表示第 i 指标比第 j 指标重要，aij= 0.5 表示第 i 指标和第 j 指标同等重要，aij= 0 表示第 i 指标没有第 j 指标重要，得到模糊优先关系矩阵 AB1，AB2，AB3如下。

（2）将模糊优先关系矩阵转换成模糊一致矩阵FB1，FB2，FB3如下。

（3）利用相关公式计算各指标优度值，得到各指标的权重 WB1= (0.244 8，0.201 2，0.287 9，0.156 6，0.109 4) ，WB2= (0.211 6，0.226 3，0.182 1，0.106 4，0.106 4，0.167 2)，WB3= (0.392 1，0.392 1，0.215 8)。

3.2根据特征值矩阵计算隶属度

（1）各位专家通过对兰州新区铁路物流中心各方案进行优缺点分析，对第三级指标层特征值打分，得到 6 个待选方案的评价特征值矩阵。在 B1层中，C1和 C2特征值取值集合为{优，良，中，差，劣}；C3特征值取值为不同方案吸引范围物流量，万 t；C4和 C5特征值取值集合为{大，较大，中，较小，小}；在 B2层中，C6和 C7特征值取值集合为{大，较大，中，较小，小}，取值根据接轨条件难度及工程条件复杂度由大到小进行取值；C8特征值取值为不同方案工程量，铺轨公里；C9和 C10特征值取值集合为{优，良，中，差，劣}；C11特征值取值集合为{大，较大，中，较小，小}。在 B3层中，C12特征值取值为总投资额，亿元；C13和 C14特征值取值集合为{优，良，中，差，劣}。以 B1层次指标为例进行计算，取值后的特征值矩阵 XB1为

同理，得到特征值矩阵 XB2，XB3如下。

（2）利用越大越优和越小越优的不同统一化公式处理特征值矩阵，得到相对隶属度矩阵如下。

3.3决策组最优决策过程

由最大隶属度原理，根据模糊关系矩阵可以建立优等方案 GB1= (1，1，1，1，1)。利用上面所得的权重，计算带权欧几里德贴近度向量值为NB1= (0.861，0.901，0.626，0.574，0.536，0.443) ，同理可以得到技术因素 B2，经济因素 B3对应的带权欧几里德贴进度向量值为 NB2= (0.880，0.874，0.554，0.761，0.731，0.461) ， NB3= (0.875，0.893，0.636，0.805，0.853，0.612)。由 B 层次各指标带权贴近度向量，可以得到 A 层次的方案相对隶属度矩阵，令 N1A= X1A。计算 A 层次各指标的权重 WA= (0.304 8，0.351 2，0.344 0)。

对于 A 层次同样应用带权欧几里得贴进度向量计算公式，计算得到第 1 个决策组对 6 个比选方案的贴近度向量，记为 N1，N1= (0.96，0.98，0.71，0.80，0.78，0.61)。同理计算得到其他 2 个决策组贴近度向量 N2= (0.85，0.89，0.73，0.69，0.65，0.72)，N3= (0.89，0.92，0.78，0.74，0.72，0.65)。

3.4相对熵集结模型求解群组最优方案

对于目前的铁路项目建设，国家明确鼓励社会资本参与，在铁总计统 [2015] 232 号文件中也多次提出引入 PPP 模式思路，对于多方投资决策的情况，如何兼顾各方诉求，拟合群偏好，需要提出一种更为科学合理的评价方法。相对熵集结模型对于多决策组方案评价具有良好的集结性，适用于多决策组的铁路物流中心方案评价。

兰州新区铁路物流中心决策方案集 T = {t1，t2，t3，t4，t5，t6}，决策群体由 3 个决策组组成 E = {e1，e2，e3}，各个决策组权重分别为 ω1= 1/2，ω2= 1/4，ω3= 1/4。根据 N1，N2，N33个决策组贴近度向量，计算得到由相对熵模型获得的群偏好权重，。因此，方案排序为 t2＞ t1＞ t3＞ t4＞ t5＞ t6，即兰州新区北站南侧方案 t2为最优方案。

4　结束语

以兰州新区铁路物流中心实例，构建兼顾社会、技术、经济因素的指标评价体系，研究采用改进 AHP 法和模糊群决策模型进行多方案评价的实用方法，解决传统铁路物流中心多方案评价比选中因素考虑不全、决策主观性强，以及 PPP 模式下多方决策意见难以达成一致等问题，对科学合理地规划建设铁路物流中心、减少决策盲目性、提高铁路建设资金效益具有重要辅助决策作用。兰州铁路局管辖范围内规划的 10 个二级铁路物流基地，目前基本开展前期工作，实践表明，该方法也可以用于二级铁路物流基地推荐方案之间的比选评价，为科学决策各二级物流基地的建设时序，统筹安排兰州铁路局范围内铁路物流中心建设提供重要参考依据。

[1] 中国铁路总公司. 中国铁路总公司关于印发《铁路物流基地布局规划及 2015—2017 年建设计划》的通知：铁总计统 [2015] 232 号[A]. 北京：中国铁路总公司，2015.

[2] 董二通. 铁路货运站向铁路物流中心转型的探讨[J]. 铁道货运，2015，33(5)：25-29. DONG Er-tong. Discussion on Transferring Railway Freight Station to Railway Logistic Center[J]. Railway Freight Transport，2015，33(5)：25-29.

[3] 中铁第一勘察设计院集团兰州院. 兰州新区铁路物流中心预可行性研究[R]. 兰州：中铁第一勘察设计院集团兰州院，2015：75-90.

[4] 林齐宁. 决策分析教程[M]. 北京：清华大学出版社，2013.

[5] 吴小欢，吕跃进，杨 芳. 模糊互补判断矩阵的一致性检验及修正[J]. 模糊系统与数学，2010，24(2)：33-36. WU Xiao-huan，LV Yue-jin，YANG Fang. The Verifier and Adjustment of Cosistency for Fuzzy Complementary Judgement Matrix [J]. Fuzzy Systems and Mathematics，2010，24(2)：33-36.

[6] 张文力. 结合模糊数学与多目标决策方法的混合多准则推荐系统[D]. 成都：电子科技大学，2013.

[7] 郭春香，郭耀煌. 属性具有不同形式偏好信息的群决策方法[J]. 系统工程与电子技术，2005 (1)：63-65. GUO Chun-xiang，GUO Yao-huang. Approach of Multipleattribute Group Decision Making with Different Forms of Preference Information[J]. Systems Engineering and Electrics，2005 (1)：63-65.

[8] 邱菀华. 管理决策熵学及其应用[M]. 北京：中国电力出版社，2011.

责任编辑：吴文娟

Study on Program Evaluation of Railway Logistics Center based on Fuzzy Group Decision-making

Based on expounding the establishment of evaluation index system of Xinqu railway logistics center in Lanzhou, targeting with 6 alternative programs, the evaluation index system of 3-levels program is established from the aspects of general index layer, sub-index layer and itemized index layer, the weight of each index is determined by using improved AHP method and the membership grade is calculated, and then, the single decision-making group programs are made ordering by using weighted Euclid approach degree, and the optimal decision-making program of group is solved by using REM assembly. Taking the multi-programs evaluation of Xinqu railway logistics center in Lanzhou as the example, this paper makes analysis and the analysis result shows the evaluation method has better application effects.

Railway Logistics Center; AHP; Fuzzy Group Decision-making; Program Evaluation

1003-1421(2016)01-0025-05

F259.22

A

10.16668/j.cnki.issn.1003-1421.2016.01.06

2015-12-18

国家自然科学基金 (61563028)