转矩波动下电动轮纵向阶次振动特性及理论分析

毛 钰， 左曙光， 林 福， 冯朝阳

(同济大学 新能源汽车工程中心， 上海 201804)



转矩波动下电动轮纵向阶次振动特性及理论分析

毛 钰， 左曙光， 林 福， 冯朝阳

(同济大学 新能源汽车工程中心， 上海 201804)

针对轮毂电机转矩波动激励引起的电动轮系统振动问题，通过台架试验测得了电动轮运行工况下振动加速度信号，揭示了电动轮系统纵向振动的阶次特征和高频特性.基于电机电磁转矩解析模型从磁场相互作用的角度分析了永磁体磁场非正弦分布和电流谐波对转矩波动的贡献，进而解释了电动轮阶次振动的来源，即电动轮6.0阶振动由永磁体非正弦分布引起；1.0阶振动主要由电流谐波引起；6.5阶振动则由电流谐波和永磁体非正弦分布共同引起.为解释电动轮高频振动现象建立了基于刚性环理论的电动轮动力学模型并进行模态分析，结果表明，电动轮3个共振峰处高频振动分别对应轮胎和车轮同向旋转、反向旋转和纵向平移模态.

电动轮； 转矩波动； 纵向高频振动； 阶次特征

轮毂电机驱动电动车作为下一代电动汽车的关键技术之一，受到学术和工程界的普遍关注[1-3].其主要结构特征是将驱动电机分别安装在各驱动轮内或附近，动力直接通过驱动电机转子传递至车轮.这种高度集成的结构使轮毂电机驱动电动车整车结构布置、底盘集成控制和操纵方便性等方面具有明显的技术优势[4].但驱动电机与车轮直接相连的电动轮结构也存在一些问题.由于电机结构因素和供电电流谐波的影响，轮毂电机电磁转矩存在波动特征[5]，转矩波动不经过机械传动部件的吸收直接作用于车轮，使得电动轮的振动问题更加突出.

同济大学于增亮等[6]对轮毂电机驱动电动汽车进行了道路试验，揭示了电动轮振动问题并指出主要振动能量集中在30～70 Hz以及100～110 Hz等频率范围，但未结合理论研究对振动特性进行分析.马琮淦等[5]建立了d-q轴坐标下的永磁同步电机转矩波动解析模型，对试验采集到的电动车用永磁同步电机转矩波动阶次特征进行了解释，但没有从根源上揭示转矩波动产生机理，而且d-q轴模型下电机的交直轴电感等参数计算估计方法复杂，通常需要借助仿真或试验才能精确获取.左曙光等[7]提出了一种电动车用永磁同步电机转矩计算和波动特性分析的解析模型，从磁场相互作用的角度分析了转矩波动阶次来源，为本文的研究提供了参考.左曙光等[8]通过电动轮台架试验实测转矩波动下电动轮振动信号，结合转矩波动特征对振动阶次进行了解释，但没有从动力学建模的角度获得电动轮模态特性并进而分析高频振动现象.张立军等[9]应用刚性环轮胎假设建立了轮毂电机-轮胎总成模型，指出电机的转矩波动会引起轮胎纵向接地力的振荡，但没有进一步关注轮胎振动响应，而且缺乏结合模型固有特性分析对仿真结果进行解释.综上所述，目前的一些文献对转矩波动下电动轮振动问题进行了揭示，但在利用综合转矩波动特征分析方法和结构动力学建模分析方法对电动轮振动特性进行研究方面还存在不足.

因此，本文首先通过台架试验测得了电动轮运行工况下振动加速度信号，揭示了电动轮系统高频阶次振动现象.其次，基于电机电磁转矩解析模型确定了转矩波动的阶次特征及其影响因素，进而对电动轮主要振动阶次来源进行解释.最后建立了基于刚性环理论的电动轮动力学模型并分析了系统固有特性，解释了电动轮共振峰处高频振动对应的模态特征.

1 电动轮系统振动测试台架试验与分析

1.1 试验设置

为分析轮毂电机驱动电动汽车在驱动电机转矩波动激励下振动特性，本文选取某电动汽车电动轮系统，将其放置在转鼓上并经由双横臂悬架与课题组开发的悬架试验台架[10]相连，调整悬架主要硬点位置和轮胎载荷以真实反映电动轮系统在实际汽车上的安装情况，如图1所示，电动轮系统采用的轮毂电机为分数槽集中绕组的外转子永磁同步电机，其参数如表1所示.电机控制器由直流稳压电源供电，控制器驱动电机旋转并控制平均转矩输出大小，转鼓给轮胎施加负载以模拟车辆行驶过程中的阻力.试验过程中由加速度传感器测量电动轮实际运行工况下轮胎加速度信号，由电流钳测量电机相电流信号，试验数据由LMS Test.Lab软件采集.

图1 电动轮台架试验布置

参数数值极对数12槽数27额定功率/kW0.8额定转矩/(N·m)26额定转速/(r·min-1)290

1.2 试验数据处理与分析

为使试验结果具有代表性，下面主要分析电机设定转矩60 N·m，转速由0加速到200 r·min-1(加速时间为20 s)工况下的结果.采集的电流及加速度信号如图2所示.对采集到的信号进行短时傅里叶变换得到其时频谱.图3为电机相电流时频图，图4a,4b分别为轮胎纵向和垂向加速度时频谱.

a 电流

b 纵向加速度

c 垂向加速度

图3 相电流时频图

a 纵向

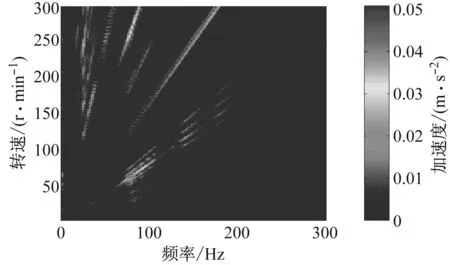
b 垂向

在电机分析中，常采用电流基频这一概念进行分析说明，电流基频为转频与极对数的乘积，即

f=pn/60

(1)

式中:f为电流基频;p为极对数；n为转速.在后面分析中涉及到的阶次均指相对电流基频，一倍的电流基频定义为1.0阶.

现有的调速永磁同步电机大多采用变频器供电，然而变频器的引入使得电流并非理想的正弦波形，而是存在丰富的谐波成分.从图3的电流时频图可以看出：电机相电流中除频率为电流基频的基波外，还存在阶次为0.5，1.5和2.0的谐波.

对比图4a，4b可知，轮胎纵向振动比垂向振动大一个数量级，这是由于转矩波动会通过轮胎与路面的附着作用引起纵向接地力波动进而激发电动轮纵向振动，即电动轮在电机转矩波动激励下主要表现为纵向振动，所以在之后分析中只考虑纵向加速度.由图4a可知，轮胎振动表现出阶次特征，主要阶次为1.0,5.0,5.5,6.0,6.5等，其中6阶振动最为明显.另外在轮胎振动的整个频率范围内存在3个共振区.为便于分析，提取轮胎时频图中6阶振动切片如图5所示，3个共振区对应频率分别为50,100及140 Hz左右，不同于路面不平度激励引起的轮胎及车辆20 Hz以下的垂向振动，轮毂电机转矩激励会引起电动轮系统高频纵向振动.

图5 轮胎6.0阶纵向加速度

2 振动阶次来源分析

为解释轮胎振动阶次来源，参照文献[7]从气隙磁场相互作用的角度建立永磁同步电机转矩计算和波动特性分析的解析模型，基于模型分析转矩波动阶次特征及主要贡献因素.

2.1 电磁转矩

永磁同步电机气隙磁场由永磁体和绕组通电后共同产生.在不考虑定子开槽影响并忽略磁路饱和的条件下，气隙磁场等于永磁体磁场和电枢反应磁场线性叠加，即

(2)

式中:Br_mag,Br_arm分别为径向永磁体磁场和径向电枢反应磁场；Bt_mag,Bt_arm分别为切向永磁体磁场和切向电枢反应磁场.在考虑电流谐波产生的电枢反应磁场时，可将各部分气隙磁场表示成如下傅里叶级数形式：

(3)

(4)

shv的值取决于h次电流谐波的相序和电枢反应磁场的谐波次数v;对于按顺相序排列的三相电流(按ABC顺序滞后120°)，shv确定原则与sv一致，对于按逆相序排列的三相电流(按ACB顺序滞后120°)，shv确定原则与sv相反.

根据麦克斯韦张量方程，切向电磁力

(5)

将切向电磁力沿圆周积分后并化简可得到如下电磁转矩:

(6)

式中:μ0为空气磁导率;r为气隙处的平均半径;la为电机的有效轴向长度.

2.2 转矩波动阶次分析

受永磁体磁极形状的影响，永磁体磁场呈现非正弦分布，其包含的空间谐波次数n为奇数.对于三相电机而言，电枢反应磁场空间谐波次数v不为3的倍数，所以为满足v=np0，n只能取6i±1，此时v=6p0i±p0=3[2p0i±(p0-1)/3]±1.根据sv和shv确定原则，由式(6)得到电磁转矩为

Te=T1+T2+T3

(7)

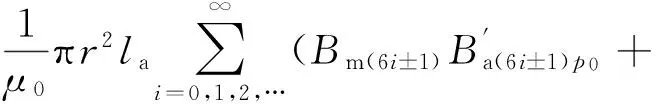
(8)

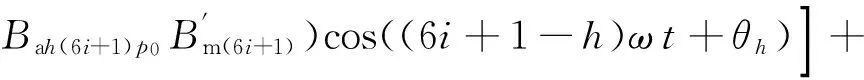
(9)

(10)

从式(8)可以看出，电磁转矩中存在6i阶转矩波动，来源于空间(6i±1)p次永磁体磁场和电流基波产生的空间同次电枢反应磁场相互作用，主要与永磁体磁场非正弦分布有关.

式(9)为与顺相序电流谐波有关的电磁转矩，从中可知电磁转矩中存在1-h，6i+1-h和6i-1+h阶转矩波动.其中1-h阶来源于永磁体基波磁场和电流谐波产生的空间p次电枢反应磁场的相互作用，主要由电流谐波引起；6i+1-h阶(或6i-1+h阶)来源于永磁体(6i+1)p次(或(6i-1)p次)磁场和顺相序电流谐波产生的空间同次电枢反应磁场相互作用产生，由永磁体磁场非正弦分布和电流谐波共同引起.

式(10)为与逆相序电流谐波有关的电磁转矩，从中可知电磁转矩中存在1+h，6i+1+h和6i-1-h阶转矩波动.其中1+h阶来源于永磁体基波磁场和电流谐波产生的空间p次电枢反应磁场的相互作用，主要由电流谐波引起；6i+1+h阶(或6i-1-h阶)来源于永磁体(6i+1)p次(或(6i-1)p次)磁场和逆相序电流谐波产生的空间同次电枢反应磁场相互作用产生，由永磁体磁场非正弦分布和电流谐波共同引起.

2.3 电动轮振动阶次解释

本文考虑试验所采用的轮毂电机具体结构，并施加试验所测得的电机相电流信号，通过有限元仿真得到60 r·min-1稳态转速下电机电磁转矩输出情况，如图6所示.

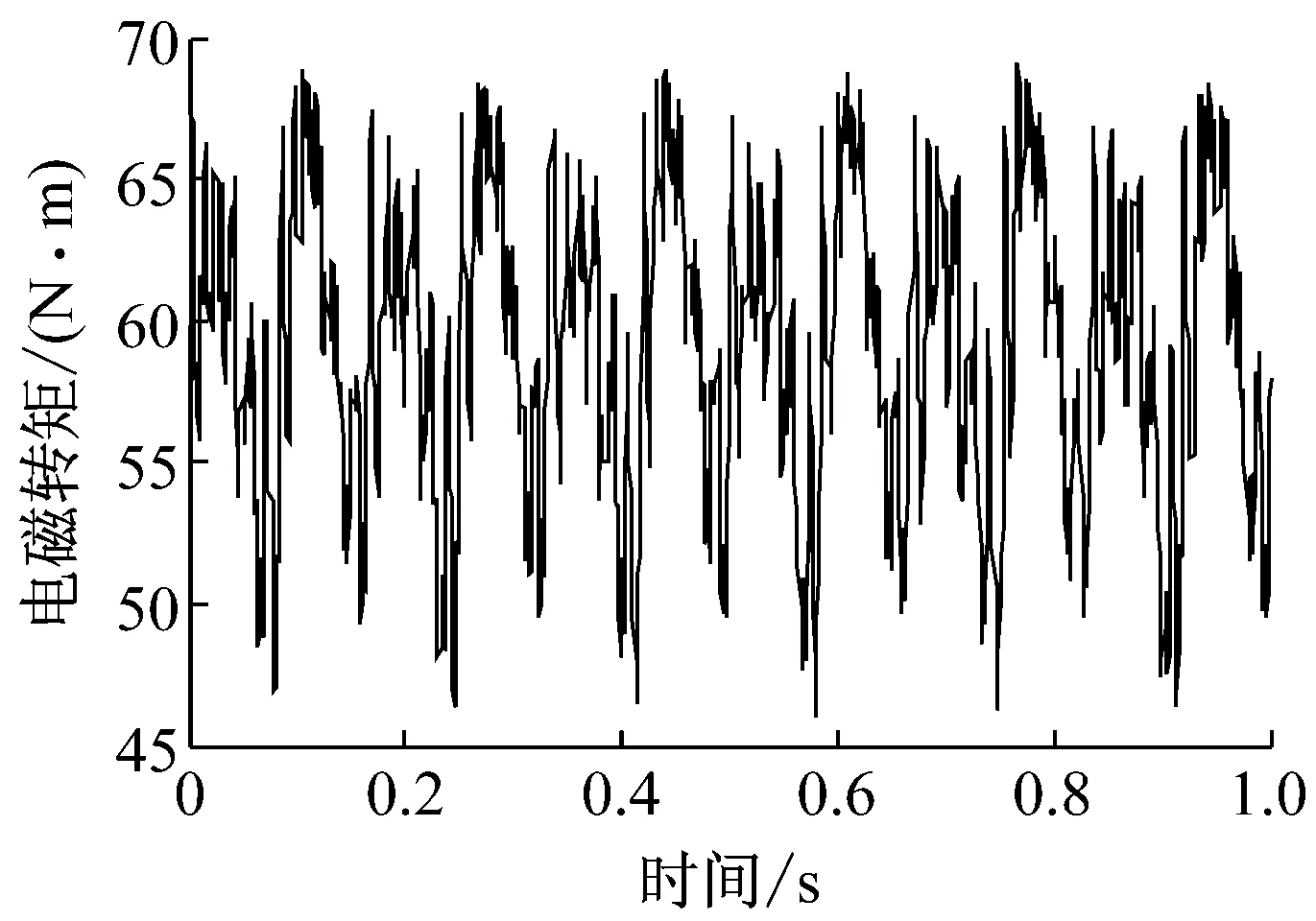
a 电磁转矩时域波形

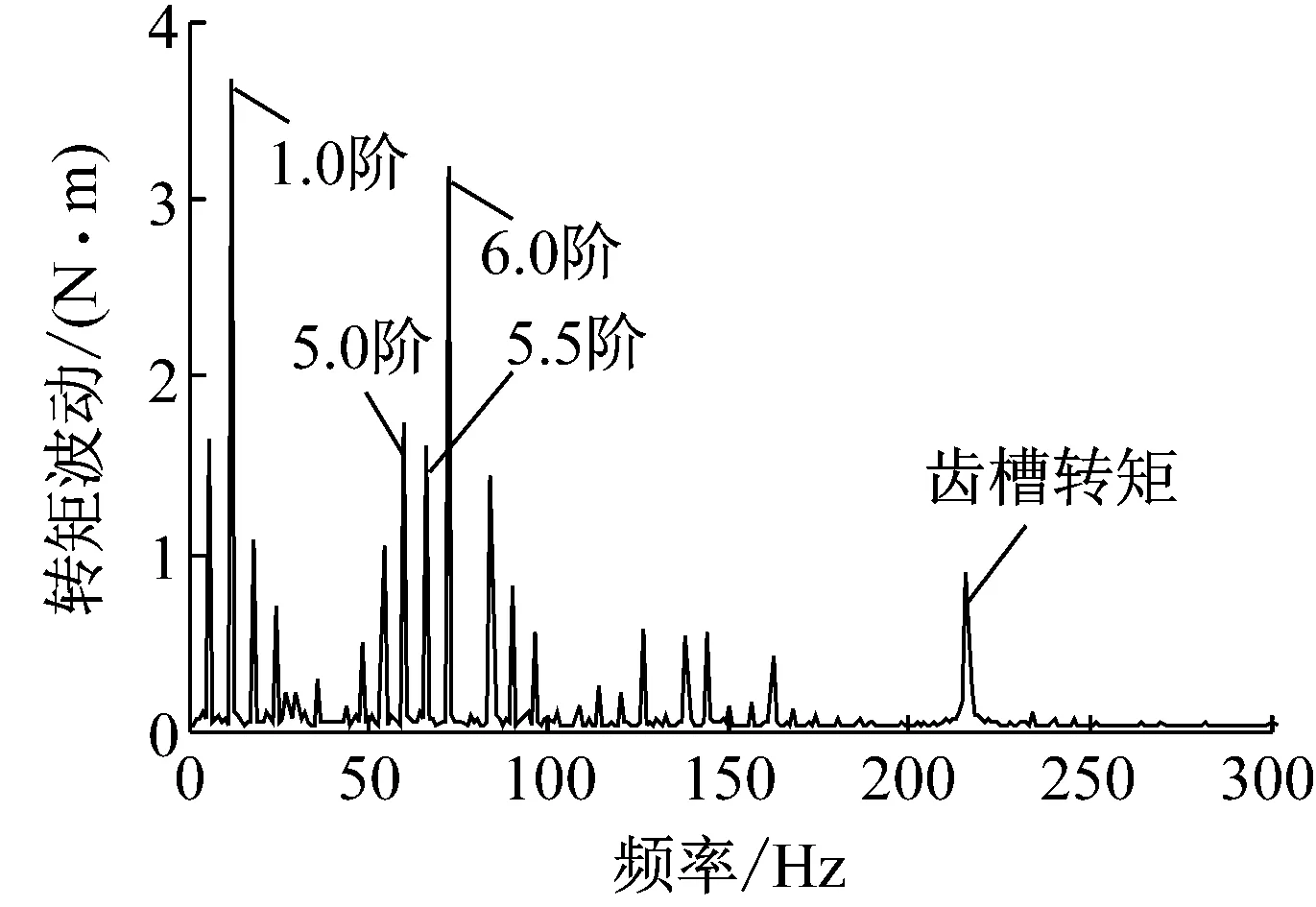
b 转矩波动频域波形

电磁转矩存在明显波动，其波动表现出阶次特征，且主要阶次为1.0,5.0,5.5,6.0阶等.结合理论分析对转矩波动阶次进行解释如下：试验采集到的0.5，1.5和2.0阶等主要电流谐波均为顺相序，所以与电流谐波相关的转矩波动阶次只有(1-h)阶、(6i+1-h)阶和(6i-1+h)阶.6阶转矩波动由永磁体磁场非正弦分布产生，来源于永磁体5p(7p)次磁场与电流基波的5p(7p)次磁场相互作用；1.0阶转矩波动由2次电流谐波产生，来源于永磁体基波磁场和电流谐波的p次磁场的相互作用；5.0阶转矩波动由2次电流谐波与永磁体磁场非正弦分布共同产生，来源于永磁体7p次磁场与电流谐波的7p次磁场的相互作用产生；5.5阶转矩波动由0.5或1.5次电流谐波与永磁体磁场非正弦分布产生，来源于永磁体5p(7p)次磁场与电流谐波的5p(7p)磁场相互作用.另外，仿真中出现了由于定子开槽引起的齿槽转矩，由于本文采用的轮毂电机为24极27槽，其齿槽转矩相对较小(齿槽转矩反比于极槽的最小公倍数)，而且齿槽转矩频率较高，引起的电动轮系统振动较小，所以在分析转矩波动时忽略了开槽的影响.转矩波动呈现的阶次特征与实测振动阶次相吻合，说明电动轮系统阶次振动由转矩波动引起，进而可解释振动阶次来源，其对应关系如表2所示.

表2 试验振动阶次来源分析

3 电动轮振动特性分析

为解释试验中观测到的电动轮振动现象，揭示振动频谱图中各共振区域对应的电动轮模态特征，本文建立了电动轮动力学模型并对其固有特性进行分析.

3.1 电动轮动力学建模

由试验结果可知，电动轮振动主要集中在150 Hz以内，在该频率范围内可不考虑轮胎胎体的变形[13]，故基于刚性环理论[14-15]对轮胎进行建模，即将轮胎等效为刚性的轮胎环，与车轮通过弹簧和阻尼器连接.在电动轮结构中轮辋和轮毂电机通过螺栓刚性相连，因此车轮包括轮辋和轮毂电机两部分.轮胎在转鼓上附着特性较好，可认为轮胎纵向接地力与滑移率成正比，因此轮胎接地模型仅需采用弹簧-阻尼器串联的一阶系统以反映胎面松弛特性.另外试验结果表明纵向振动比垂向振动更明显，因此在建模时忽略系统垂向自由度，简化后的电动轮系统如图7所示.

图7 简化的电动轮振动系统

由牛顿第二定律确定电动轮系统动力学方程如下：

(11)

式中:Iby，Idy分别为轮胎环和车轮转动惯量；θb，θd分别为轮胎环和车轮旋转弧度；Md为轮毂电机转矩；Fcx为轮胎纵向力；Re为轮胎半径；kb，cb分别为轮胎平移刚度和阻尼；kbθ，cbθ分别为轮胎旋转刚度和阻尼；kux，cux分别为悬架衬套刚度和阻尼；kc为胎面纵向刚度；cc为胎面纵向阻尼；mb，ma分别为轮胎环和车轮质量；xb,xa分别为轮胎环和车轮纵向位移.其中质量参数可通过测量获得，刚度阻尼参数由模态试验确定，相应确定过程见文献[16-17]，具体参数数值见表3.

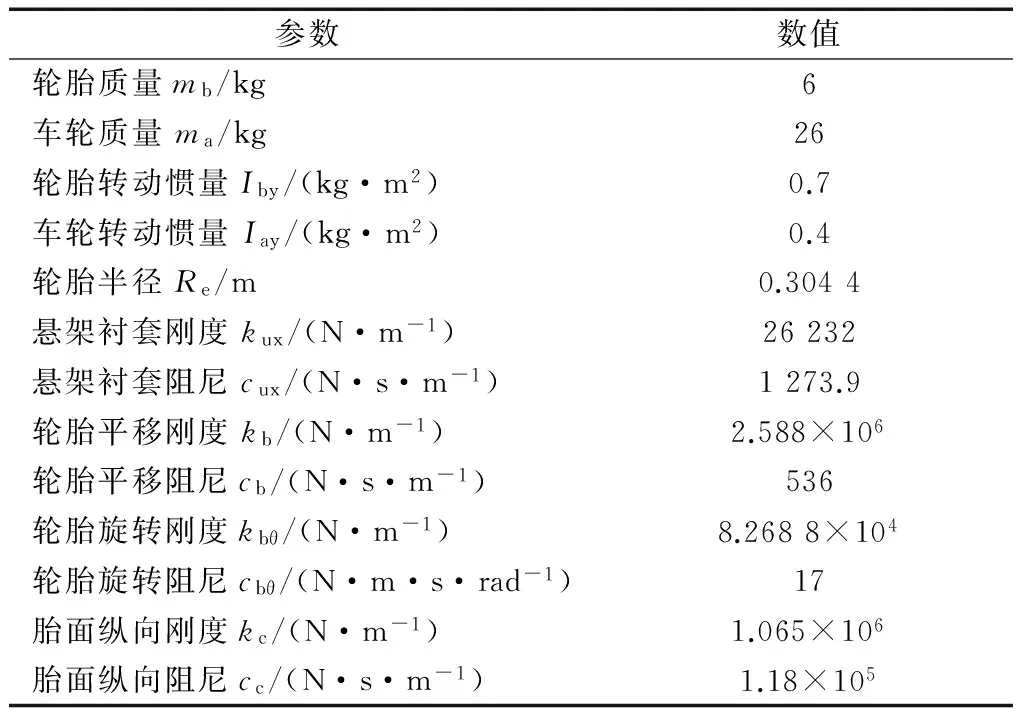
表3 电动轮主要参数

3.2 电动轮模态分析

由式(11)确定的以轮毂电机转矩为输入、轮胎振动加速度为输出的电动轮振动系统是一个线性定常系统，为基于线性系统理论进行分析并进而确定电动轮模态特征，将式(11)表达成如下状态空间形式：

(12)

式中：状态变量为

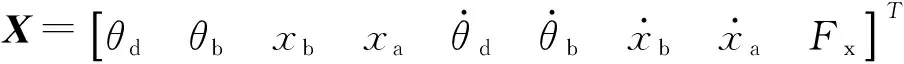
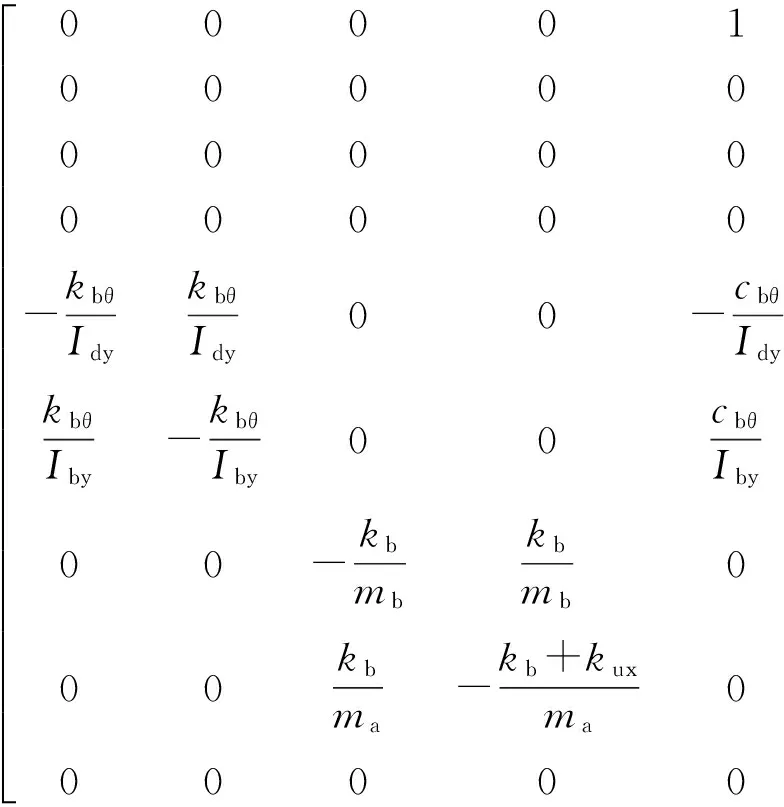
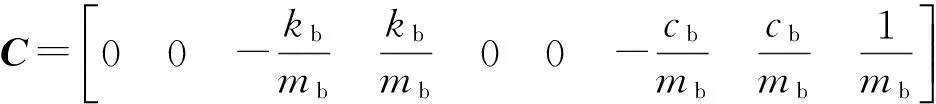
D=0.

按式(13)求解系统矩阵A的特征值和特征向量

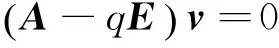
(13)

式中:E为单位阵;v为特征向量;q为特征值，实特征值对应的系统响应不存在振荡，对振动特性无影响；共轭出现的复特征值引起系统有阻尼振动，对应于振动系统的各阶模态，特征值可表示成如下形式:

(14)

式中：ζ为模态阻尼比；ωn为无阻尼模态频率.矩阵A的4对共轭特征值及对应的4阶模态参数如表4所示.

表4 电动轮模态参数

根据式(13)可求得各特征值对应的特征向量，进而确定各阶复模态振型.由表4可知各阶模态阻尼比都较小，系统具有欠阻尼特性，因此为分析模态主要振动特征，仅提取实部得到各阶实模态振型如图8所示.

由图8可知，1阶模态振型表现为电动轮整体的平移振动，其对应频率为3.89 Hz；2阶模态振型主要表现为轮胎环和车轮的同向旋转振动，其对应频率为45.15 Hz；3阶模态振型主要表现为轮胎环和车轮的反向旋转振动，其对应频率为95.00 Hz；4阶模态振型主要表现为轮胎环的纵向平移振动，其对应频率为136.00 Hz.

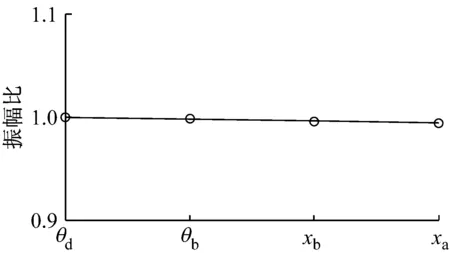
a 一阶主振型

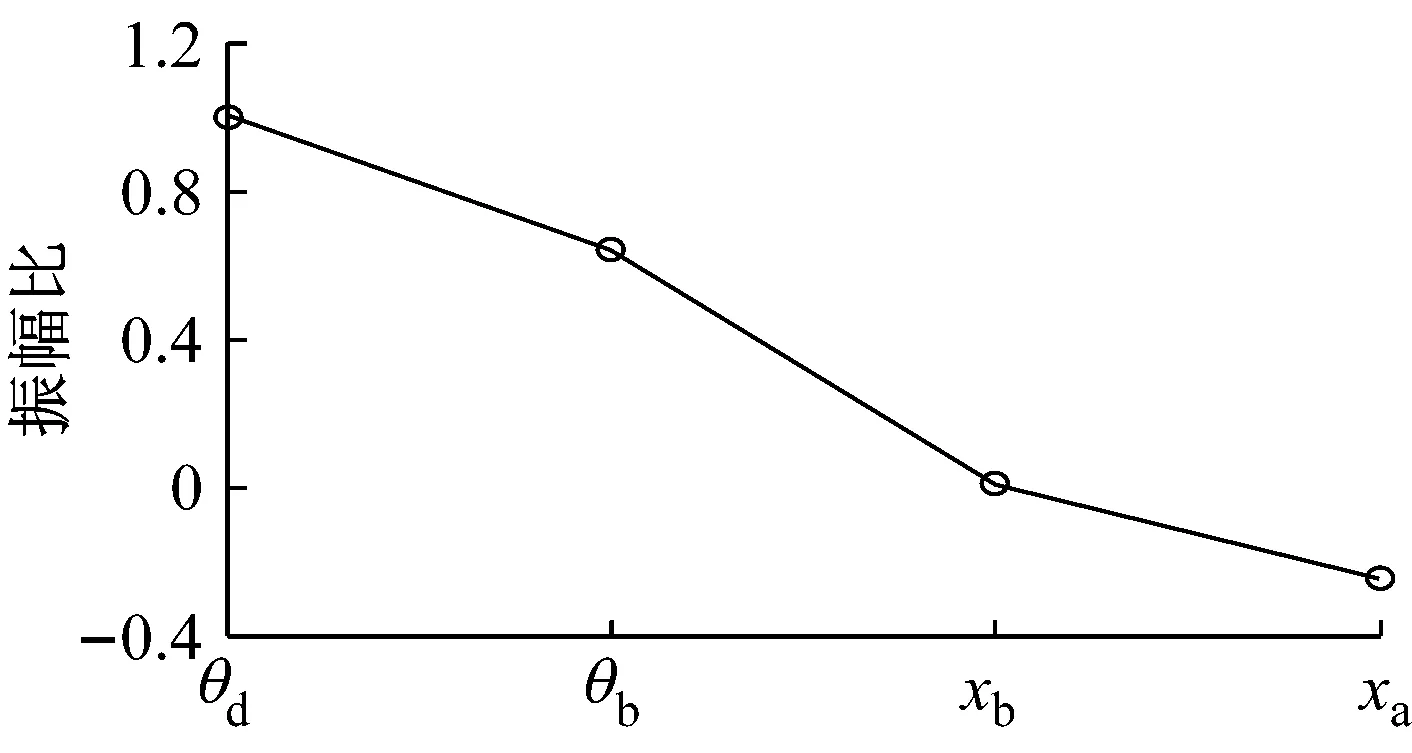
b 二阶主振型

c 三阶主振型

d 四阶主振型

3.3 电动轮高频共振现象解释

为分析各阶模态对轮毂电机转矩下轮胎纵向振动的贡献，从而对试验振动信号频谱中共振区进行解释，根据电动轮系统状态方程确定轮毂电机转矩波动到轮胎纵向振动加速度传递曲线如图9所示.图9中存在3个明显峰值，其频率及相对大小与试验结果中出现的共振峰(图5)吻合较好.3个共振频率分别对应轮胎环和轮辋间同向旋转、反向旋转和轮胎纵向平移模态频率，其中反向旋转模态对应的峰值最为突出.由于转矩波动具有阶次特征，在电机0～300 r·min-1加速工况下，6.0阶转矩波动频率涵盖0～360 Hz，当转矩波动频率接近上述3个阶次模态频率时引起电动轮系统共振，因此电动轮系统表现为能量集中在50，100和140 Hz附近的高频振动.

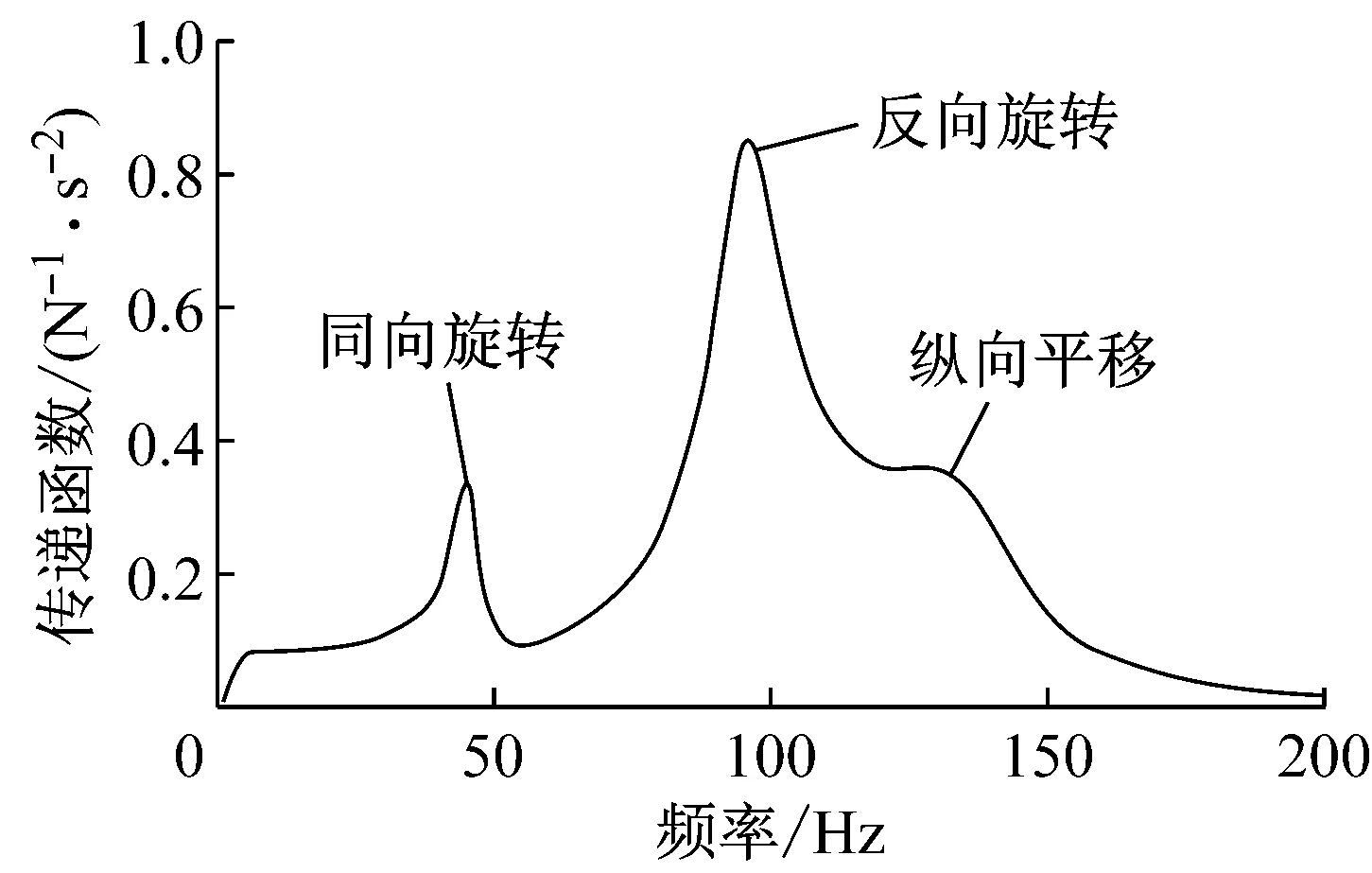
图9 轮毂转矩到轮胎纵向振动加速度传递曲线

4 结论

本文进行了电动轮系统振动测试台架试验，揭示了转矩波动激励下电动轮阶次振动特征和高频振动特性，并结合理论分析较好地解释了电动轮振动阶次来源和高频共振区对应模态特征，得到以下结论：

(1) 由于电流谐波和永磁体磁场非正弦分布的影响，永磁同步电机电磁转矩表现出阶次波动特征，并进一步引起电动轮阶次振动.其中电动轮6.0阶振动来源于永磁体磁场非正弦分布引起的6.0阶转矩波动；1.0阶振动主要由2次电流谐波引起；5.0阶振动由2次电流谐波与永磁体磁场非正弦分布共同引起；5.5，6.5阶振动由0.5或1.5次电流谐波与永磁体磁场非正弦分布共同引起.

(2) 轮胎环和车轮间同向旋转、反向旋转和轮胎纵向平移模态对轮毂电机转矩波动下电动轮纵向振动贡献明显，由于以上3个阶次模态对应的频率一般处于50～150 Hz范围，不同于路面不平度激励引起的轮胎及车辆20 Hz以下的振动，轮毂电机转矩会引起电动轮纵向高频振动.

[1] Huang X Y, Wang J M. Model predictive regenerative braking control for lightweight electric vehicles with in wheel motors[J]. Proceedings of the Institution of Mechanical Engineerings Part D:Journal of Automobile Engineering, 2012, 226(9): 1220.

[2] Chen Y, Wang J M. Design and evaluation on electric differentials for overactuated electric ground vehicles with four independent in-wheel motors[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1535.

[3] Wang R, Chen Y, Feng D,etal. Development and performance characterization of an electric ground vehicle with independently-actuated in-wheel motors[J]. Journal of Power Sources, 2011, 196(8): 3962.

[4] Luo Y T, Tan D. Study on the dynamics of the in-wheel motor system[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3510.

[5] 马琮淦，左曙光，杨德良，等. 电动车用永磁同步电机的转矩阶次特征分析[J]. 振动与冲击, 2013, 32(13): 81.

MA Conggan, ZUO Shuguang, Yang Deliang,etal. Order feature analysis for torque ripple of permanent magnet synchronous motor for an electric vehicle[J]. Journal of Vibration and Shock, 2013, 32(13): 81.

[6] 于增亮，张立军，孙北. 轮毂电机驱动电动微型车车内噪声道路试验分析[J]. 上海汽车，2009(8): 8．

YU Zengliang, ZHANG Lijun, SUN Bei. Road test analysis for interior noise of wheel-hub motor driven micro electric vehicle[J]. Shanghai Auto, 2009(8): 8.

[7] 左曙光，林福，吴旭东. 车用永磁同步电机转矩解析模型和波动特性分析[J]. 浙江大学学报:工学版，2015，49(9)：1731.

ZUO Shuguang, LIN Fu, WU Xudong. Analytical calculation model and ripple characteristics analysis of torque in permanent magnet synchronous motor for electric vehicles[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(9): 1731.

[8] 左曙光，段向雷，吴旭东. 电动轮-悬架系统台架振动特性试验分析[J]. 振动与冲击, 2014, 33(12): 165.

ZUO Shuguang, DUAN Xianglei, WU Xudong. Vibration test analysis of a electric wheel-suspension system on a test bed[J]. Journal of Vibration and Shock, 2014, 33(12): 165.

[9] 张立军，钱敏，余卓平. 轮毂电机-轮胎总成非线性动力学特性仿真分析[C]∥第五届中国智能交通年会暨第六届国际节能与新能源汽车创新发展论坛优秀论文集:下册. 北京: 电子工业出版社, 2009: 162-168.

ZAHNG Lijun, QIAN Min, YU Zhuoping. Simulation and analysis of the nonlinear dynamic characteristics of in-wheel motor and tire system[C]//Proceedings of the 5th China Annual Conference and Exhibition on Intelligent Transport System. Beijng: Publishing House of Electronics Industry, 2009: 162-168.

[10] 同济大学. 一种可调式电动轮悬架系统振动噪声测试台：中国，201310125584.0[P]. [2013-08-07].

Tongji University. An adjustable vibration and noise test bench of electric wheel system: China, 201310125584.0[P]. [2013-08-07].

[11] Zhu Z Q，Howe D，Chan C C．Improved analytical model for predicting the magnetic field distribution in brushless permanent-magnet machines[J]．IEEE Transactions on Magnetics, 2002，38(1)：229．

[12] 王秀和．永磁电机[M]．北京：中国电力出版社，2011．

WANG Xiuhe. Permanent magnet motor[M]. Beijing: China Electric Power Press, 2011.

[13] 庄继德．现代汽车轮胎技术[M]．北京: 北 京 理 工 大 学 出版社，2001．

ZHUANG Jide. Modern automobile tire technology[M]. Beijing: Beijing Institute of Technology Press, 2001.

[14] Zegelaar. Dynamic tyre responses to brake torque variations[J]. Vehicle System Dynamics, 1997(27):65.

[15] Gipser M. FTire-the tire simulation model for all applications related to vehicle dynamics[J]. Vehicle System Dynamics, 2007(45)：139.

[16] 左曙光，段向雷，吴旭东. 电动轮刚性环耦合特性模型建模与分析[J]. 同济大学学报:自然科学版, 2014, 42(10): 1578.

ZUO Shuguang, DUAN Xianglei, WU Xudong. Modeling and analysis of rigid ring coupling model of electric wheel[J]. Journal of Tongji University: Natural Science, 2014, 42(10): 1578.

[17] 左曙光, 毛钰, 吴旭东, 等. 基于柔性环轮胎模型的电动轮固有特性分析[J]. 振动与冲击, 2016, 35(3)：41.

ZUO Shuguang, Maoyu, WU Xudong. Inherent characteristic analysis of the electric wheel based on a flexible ring model[J]. Journal of Vibration and Shock, 2016, 35(3)：41.

Experimental and Theoretical Analysis of Horizontal Order Vibration Characteristics of Electric Wheel Under Torque Ripple

MAO Yu, ZUO Shuguang, LIN Fu, FENG Zhaoyang

(Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China)

In order to study the new electric wheel vibration problems caused by torque ripple, the electric wheel vibrations under working conditions were measured in bench experiment, and order features and high-frequency characteristics of tire horizontal vibration were revealed. Based on analytical model of electromagnetic torque, and considering non-sinusoidal magnetic field distribution and current harmonics, torque ripple features were analyzed from the point of view of magnetic field interaction. Then, the order features of tire vibration were explained by source analysis of torque ripple. The 6th order vibration arises from non-sinusoidal magnetic field distribution while the first order vibration arises from current harmonics, and the 5.0th, 5.5th and 6.5th order vibrations arise from the interaction of non-sinusoidal magnetic field distribution and current harmonics. Based on the rigid ring tire assumption, the dynamics model of electric wheel system was established and modal analysis was conducted.

electric wheel; torque ripple; horizontal high-frequency vibration; order feature

2015-11-25

国家自然科学基金(51375343)； 上海市教委科研创新项目(15ZZ015)

毛 钰(1992—)，男，博士生,主要研究方向为电动轮系统振动与控制.E-mail:maoyu1224@163.com

左曙光(1968—)，男，教授，博士生导师,工学博士，主要研究方向为汽车系统动力学与控制.E-mail:sgzuo@tongji.edu.cn

U463.3

A