工程橡胶元件弹性特征参数的确定方法

刘 艳, 张济民, 罗雁云, 李秋彤

(1.同济大学 机械与能源工程学院， 上海 201804； 2.同济大学 铁道与城市轨道交通研究院， 上海 201804)



工程橡胶元件弹性特征参数的确定方法

刘 艳1,2, 张济民1,2, 罗雁云2, 李秋彤2

(1.同济大学 机械与能源工程学院， 上海 201804； 2.同济大学 铁道与城市轨道交通研究院， 上海 201804)

对橡胶材料进行大形变单轴拉伸、单轴压缩和平面拉伸试验，基于非线性弹性理论拟合得出超弹性模型参数，一方面通过数值计算完整定义材料的初始剪切模量、杨氏模量、体积压缩模量、表征压缩模量，另一方面通过仿真分析准确预测大形变范围的非线性特征以及弹性体压缩变形应力-应变关系对试件尺寸和试验边界条件的依赖性.而后，基于线弹性理论进行小形变单轴拉伸和压缩试验，并计算线性模量.分析结果表明，线性理论仅适用于拉伸和剪切小形变弹性体，而对于发生大形变或以压缩为主的复杂形变弹性体而言，大形变试验结合非线性理论和仿真分析是获取有效弹性特征参数的最佳手段.

工程橡胶； 剪切模量;杨氏模量； 体积压缩模量； 表征压缩模量； 有限元分析

橡胶材料作为最普遍的工程材料之一，具有高柔软度、高延展性及高回弹特性.对工程橡胶材料弹性特征的掌握控制是使其广泛应用于工程领域及振动控制领域的前提基础，通过试验结合数值理论确定其特征参数是指导橡胶类弹性体几何设计和优化的必要条件.弹性体各向同性，主要形变形式为拉伸、剪切和压缩，准静态弹性行为通过杨氏模量、剪切模量、表征压缩模量和体积压缩模量或泊松比加以描述[1].对于配方已确定的一种橡胶材料，工程应用分析需首先通过力学性能试验确定其机械特性，而后结合数值理论加以描述，从而指导优化设计过程.本文仅考虑准静态弹性特性，动态特性及阻尼特征将在后续研究中展开.一般而言，6种试验形式可用于完整测试橡胶材料弹性特性：单轴拉伸、单轴压缩、等双轴拉伸、平面拉伸(纯剪切)、简单剪切以及体积压缩试验.单轴拉伸和简单剪切试验是测试橡胶元件弹性的最低要求，当工程橡胶元件内部产生较大的压缩变形且边界条件相对严格时还应当补充轴向压缩及体积压缩试验[2].由于汽车、轨道等工程领域的弹性体实际工作状态为压缩、拉伸以及剪切混合变形，因此最常用且完整的试验组合为单轴拉伸、单轴压缩或等轴拉伸以及平面拉伸试验.为确保试验结果不受材料黏性特性的影响，加载、卸载过程尽量保持慢速[3].当橡胶材料在实际工程应用中发生小于25%的拉伸/压缩形变或小于65%的剪切形变时，可应用线弹性理论通过力学试验确定其线弹性模量[1,4].然而，当某些工程橡胶元件工作常态应变量大于上述应变值，线弹性模量则不能准确定义其固有的非线性弹性属性，此时需要根据超弹性理论结合试验手段获取非线性弹性特征.此外，当工程元件的优化过程采用数值仿真方法时，为保证仿真精度，橡胶元件应变量大于5%时即应当采用线性弹性理论进行分析[5-6]，有利于准确预测压缩模量对试件几何尺寸和试验边界条件的依赖性[7-8].

本文首先基于非线性弹性理论，对一种橡胶材料进行大形变单轴拉伸、单轴压缩和平面拉伸试验，通过数值分析确定其超弹性模型参数以及初始剪切模量、体积压缩模量和杨氏模量；而后基于线弹性理论进行小形变单轴拉伸和压缩试验，并对单轴压缩试验进行试件尺寸和边界条件相关性研究，计算得出线弹性模量和表征压缩模量.进而利用有限元手段采用非线性模型对大形变单轴拉伸、单轴压缩及平面拉伸试验进行仿真分析，预测不同测试工况下的单轴压缩应力-应变关系特征.分析结果将验证大形变试验和非线性理论的合理性和优越性，尤其当橡胶元件处于压缩为主的复杂形变状态.本文对工程橡胶弹性特征参数的确定方法进行研究，将为弹性体的实际应用和测试、设计以及优化过程提供理论支持和参考.

1 试验方法和测试结果

1.1 大形变试验

1.1.1 单轴拉伸试验

拉伸试件为5个条形长方体，厚度为(2±0.2)mm，宽为(10±0.2)mm；试件总长为(150±0.2)mm，实际测试长度为(50±0.2)mm，如图1所示.逐一测量每个试件测试区域的实际尺寸，平均值用于计算试件横截面积.当任意测量值与平均值误差超过2%时，该试件作废，另加以补充.试验采用小量程万能试验机Zwich/Roell Z020加载.单轴拉伸试验重复进行5次，以确保试验结果准确可靠.所有试件在试验开始48 h以前静置于试验室内，保持室温约23 ℃左右.试验开始，首先对试件进行预变形处理，以去除Mullins效应[9]，以50 mm·min-1的位移加载速度达到100%的拉伸应变后，卸载至0，重复3次.第4个加载循环开始时，记录时间-位移-载荷响应.

1.1.2 单轴压缩试验

杨氏模量并不能完整定义橡胶材料的弹性特征[8].本文单轴压缩试验过程及细节按照试验标准BS ISO 7743进行，试验装置和试件如图2所示.为减小摩擦，橡胶试件静置于两聚四氟乙烯(PTFE)块之间，进行垂向加载.原因在于：PTFE材料密度较低，不会给试件带来初始变形；PTFE材料具有极低的摩擦系数(f≈0.05)，可有效去除橡胶试件表面的横向摩擦.压缩试件是直径为(29±0.5)mm，高为(12±0.5)mm的圆柱形橡胶体.测试开始之前，进行实际尺寸测量和测试温度控制.强迫压缩变形速度为50 mm·min-1，最大变形量为50%.每个试件进行预变形处理3次，第4次加载开始记录试验数据.

图1 单轴拉伸试验

Fig.1 Uniaxial tension test

图2 单轴压缩试验

1.1.3 平面拉伸试验

橡胶材料平面拉伸试验细节尚未有权威试验标准加以规范，本文参考相关文献[10-11]完成试验.平面拉伸试验结果对试件长宽比十分敏感.当长边被牢牢固定，长边尺寸远大于宽度和厚度时，试件中心部位则沿厚度方向发生收缩，沿高度方向发生拉伸，沿45°方向发生纯剪切变形[12].如图3所示，试验仪器为安装了特殊夹具的万能试验机，试件呈薄片形，长约(120±0.5)mm，前后两侧及上下两端均粘贴有铝片，长度约(140±0.5)mm，中间的试验测试区域宽度约(12±0.2)mm.为加强铝片对橡胶试件沿长度方向的约束，确保轴向加载均匀，4对螺栓将铝片固定于加载工装内.同理，试验备有5个平面拉伸试件，仔细测量每个试件的厚度(约为(2±0.2)mm)，去除误差大于2%的试件并加以补充.试验加载速度为15 mm·min-1，目标变形值100%.加载过程中仔细观察铝件与橡胶试件的粘结状况，当发生剥离后试验数据视为无效.

图3 平面拉伸试验

1.2 小形变试验

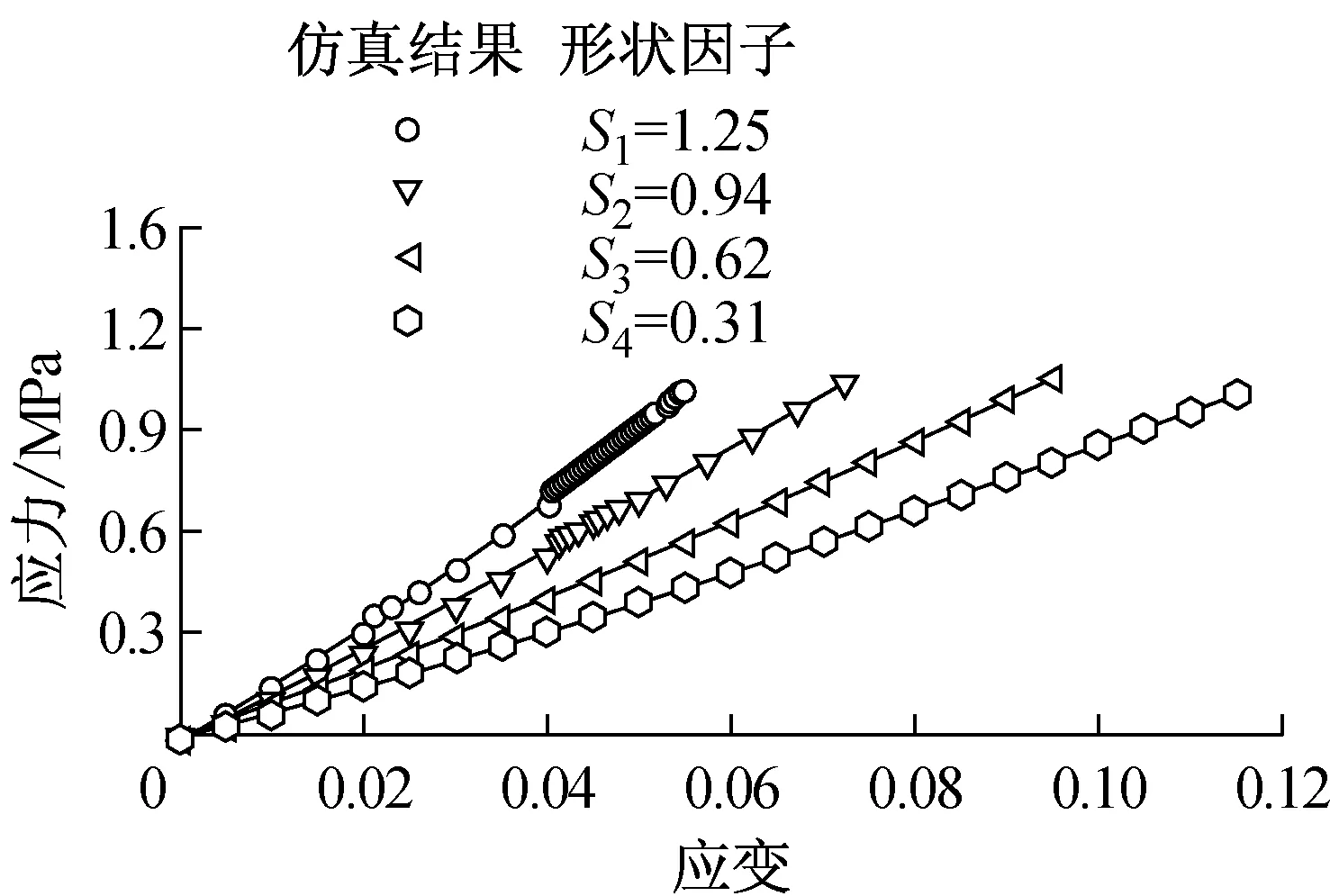
橡胶材料具有承受大弹性形变的能力，然而实际应用中某些弹性体只承受较小形变，拉伸和压缩往往小于25%，剪切小于65%.此时可进行小形变试验，结合线弹性理论确定线性模量.由于小形变范围内，线性拉伸与剪切模量呈正比关系，而单轴压缩应力-应变关系对试件尺寸和边界约束条件十分敏感，因此，本文分别进行了单轴拉伸和单轴压缩小形变测试.前者试件几何尺寸、试验仪器以及测试步骤均与大形变单轴拉伸试验保持一致，但拉伸量控制在20%以下.而压缩试验，首先采用与大形变测试过程相同的试件尺寸和边界条件，即直径d=29 mm，高度h=12 mm的圆柱形橡胶体，试件上、下表面均采用润滑处理的PTFE块，但最大压缩应变减小至约15%.为了进一步研究边界条件对试验结果的影响，两组对比试验分别将试件上、下PTFE块更换为充分润滑的铁块和无润滑处理的铁块，以模拟不同的边界条件，3种边界条件的对比试验均采用直径d=29 mm，高度h=12 mm的试件完成.为了研究试件尺寸对测试结果的影响，除了直径d=29 mm的圆柱体试件以外，补充实验还对直径为60, 45, 15 mm，高度12 mm保持不变的3种试件进行了比对试验，4种尺寸试件的测试分别在充分润滑的PTFE块以及未经润滑处理的铁块上进行.若定义形状因子S为圆柱体试件单一承载面积与可自由膨胀总面积的比值，则直径为60, 45, 29和15 mm的试件形状因子可分别表示为S1=1.25，S2=0.94，S3=0.61，S4=0.31.试验仪器和加载速度等测试细节与大形变单轴压缩试验保持一致.

1.3 测试结果

大形变单轴拉伸、单轴压缩以及平面拉伸试验测试结果如图4实线所示：单轴拉伸应变最大值约为100%；单轴压缩应变量约为50%；平面拉伸试验达到一定应变量以后，铝件与橡胶试件的黏结面发生剥离，因此未能达到目标应变100%，但应变值仍属于大形变范围，大于65%.上述3条曲线均在大形变范围内出现不同程度的硬化现象，其中单轴压缩试验非线性特征最为显著.

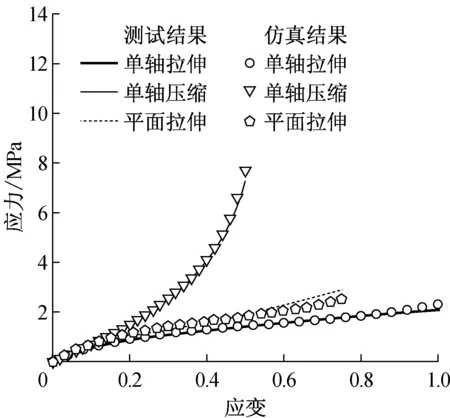
图4 仿真结果与试验结果对比

小形变单轴拉伸测试结果如图5a实线所示，最大应变值约为20%，该应力-应变关系具有良好的线性特征；直径d=29 mm，形状因子S3=0.61，边界条件由充分润滑的PTFE块提供的小形变单轴压缩测试结果如图5b实线所示，最大应变量约为18%，线性特性良好.图6中实线描述了相同试件(d=29 mm，S3=0.61)在3种边界条件下测得的应力应变关系：①充分润滑的PTFE块，f=0；②经过润滑处理的铁块，f=0.3；③未做润滑处理的铁块，f=0.5.3种逐渐趋于严格的边界条件使表征压缩模量逐渐增大.图7a和7b分别给出了边界条件①和③下，4种试件测得的应力-应变特征曲线.由图7a可知，当边界横向摩擦被充分消除时，试件几何尺寸对表征压缩模量几乎无影响；而图7b中，当边界条件存在横向约束时，测试结果对试件几何尺寸较为敏感，实测表征压缩模量随形状因子的增大而增大，即扁平试件在上、下表面存在横向约束的测试条件下表征压缩模量大于材料实际压缩模量.

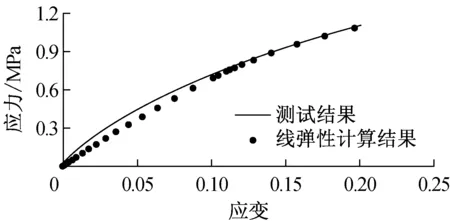
a 小形变单轴拉伸

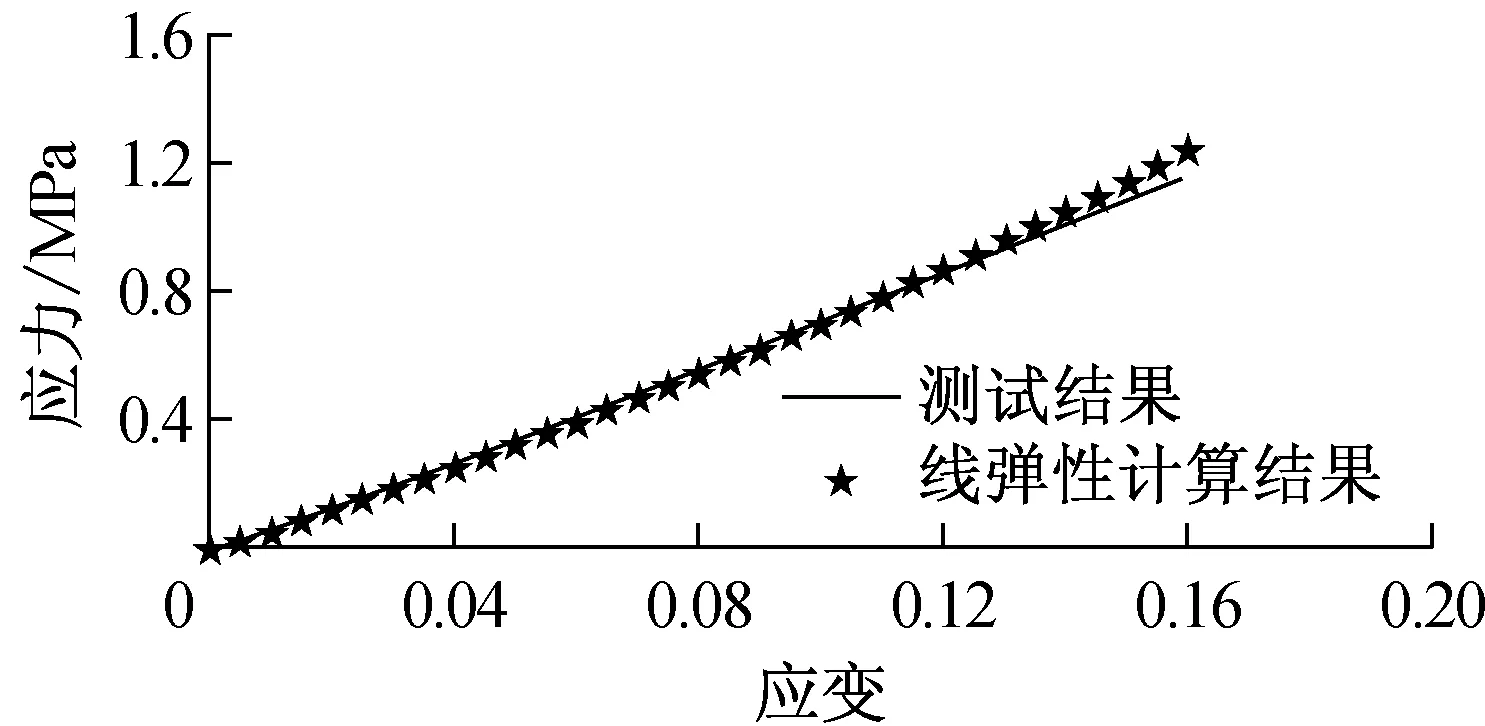
b 小形变单轴压缩

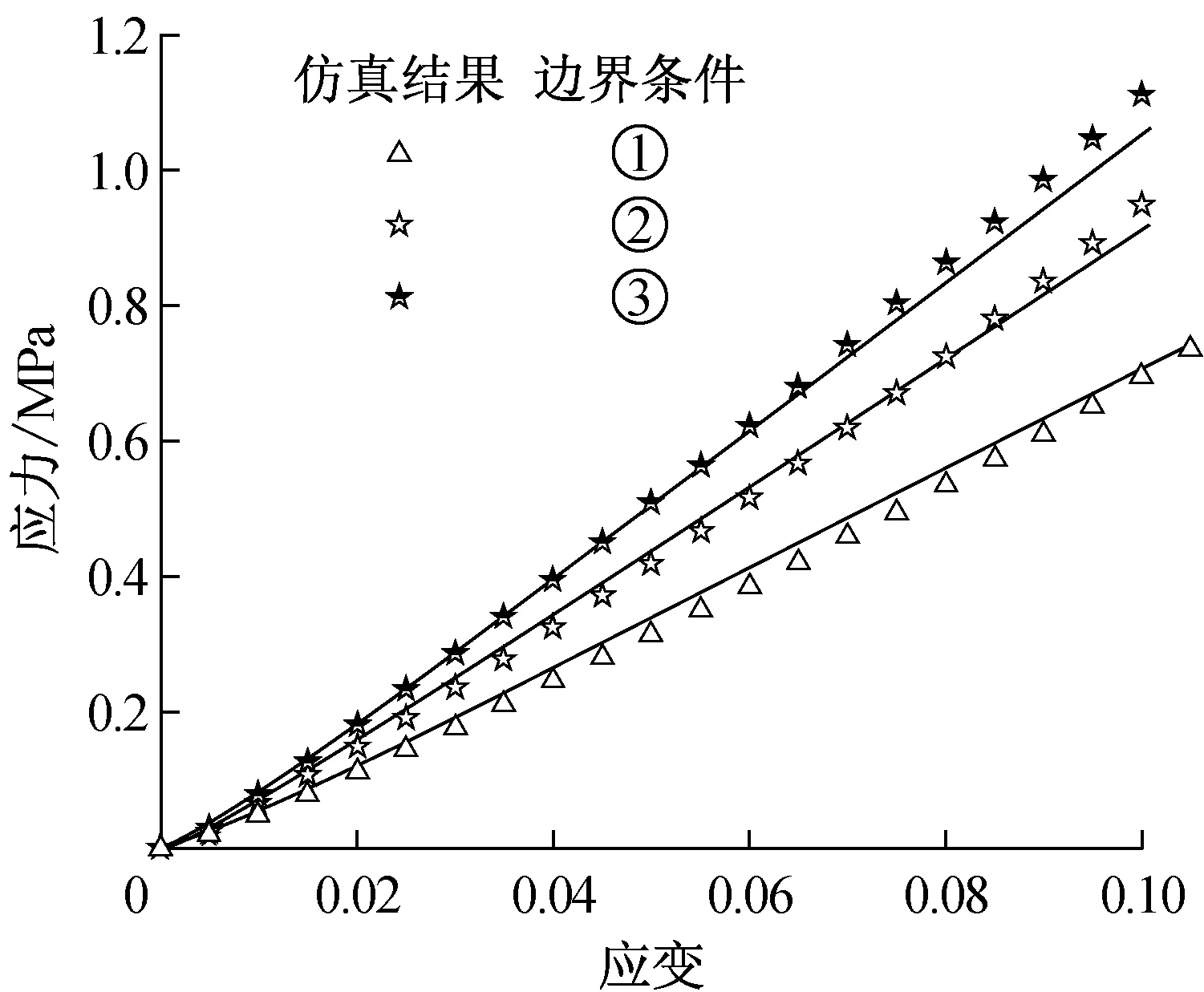
图6 边界条件影响下的小形变单轴压缩

2 理论分析

2.1 模型选取及参数拟合

处于大形变状态的橡胶工程元件，其固有非线性属性无法通过传统线性理论进行描述，而需要采用超弹性模型进行模拟.超弹性模型基于材料各项同性的基本假设，通过应变能函数定义单位体积内储存的应变能，记为W.较成熟的超弹性本构模型大多内嵌于Abaqus中，比如Mooney Rivlin、高阶多项式、减缩型多项式、Neo Hookean、Yeoh、Arruda Boyce、Van der Waals以及Ogden模型等[13].应变能函数既可定义为各方向主拉伸比λi的函数，也可定义为应变常量Ii的函数，即

W=W(I1,I2,I3) 或W=W(λ1,λ2,λ3)

(1)

a f=0

b f=0.5

(2)

拉伸比定义为拉伸后的尺寸L与拉伸前的尺寸L0之比，即λ=L/L0=1+(L-L0)/L0=1+ε，ε为工程应变.主应力可定义为

(3)

对于单轴拉伸和单轴压缩试验而言，λ2=λ3，于是

(4)

对于平面拉伸，有

(5)

其中，λ1，λ2，λ3分别表示加载方向、宽度方向以及厚度方向拉伸比.

根据大形变测试结果，采用非线性最小二乘法对Mooney Rivlin，Poly-N2，Neo Hookean，Yeoh，Arruda Boyce，Van der Waals以及一阶和三阶Ogden模型分别进行参数拟合，均方根误差详见表1.表中Van der Waals对单轴拉伸、单轴压缩、平面拉伸试验的拟合结果具有较小均方根(RMS)误差，可知其最能准确描述该组橡胶材料在不同应变状态下的超弹性特性.Van der Waals模型表达式为

(6)

(7)

(8)

式(6)～(8)中：μ为初始剪切模量；λm,a,η为材料参数.参数拟合结果见表2.此外，该组材料的邵氏硬度HA=70°，泊松比λ=0.495.

另一方面，可根据小形变试验结果拟合得到线弹性模量和不同试验条件下的表征压缩模量，详见表3.由于橡胶材料的特殊性，线性拉伸模量与表征压缩模量差值较大，不同测试边界条件和试件几何尺寸下测得的压缩模量亦有所区别.尤其当边界条件相对严格时，压缩试件上、下表面横向约束力较大，表征压缩模量对试件尺寸十分敏感.

表1 最小二乘法均方根误差

表2 Van der Waals模型参数拟合结果

表3 线弹性杨氏模量及表征压缩模量拟合结果

2.2 分析和讨论

2.2.1 超弹性与线弹性特征参数对比

已知大形变试验测试结果及Van der Waals模型数值拟合结果，可通过表达式

(9)

确定材料体积压缩模量B=204.72 MPa.再通过表达式

(10)

确定材料杨氏模量E0=6.14 MPa.

另一方面，由小形变单轴拉伸试验结果可知材料线性范围内的弹性模量约为6 MPa，即Elin=6.00 MPa，结合公式(10)可得线性剪切模量Glin=2.00 MPa，该组小形变试验获得的Elin和Glin与大形变试验测得的初始杨氏模量E0和剪切模量μ=G0基本保持一致.

2.2.2 表征压缩模量与杨氏模量的关系

如图5～7和表3可知，小形变单轴拉伸试验能够较准确地确定杨氏模量，但表征压缩模量却对测试条件和试件几何参数十分敏感，小形变试验获取的杨氏模量与压缩模量的内在关联需采用不同的理论模型加以描述才能满足，最常见的关系预测公式如下：

Ea/E=[1+3λ(1-λ)/(1+λ)/S2]/

[1+3λ(1-2λ)S2]

(11)

1/Ea=1/E/(1+2φS2)+1/B

(12)

1/Ea=1/E/(1.2+2S2)+1/B

(13)

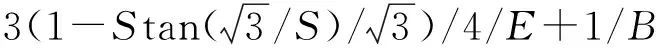
(14)

式(11)～(14)中：Ea为表征压缩模量；E为杨氏模量；S为形状因子；B为体积模量；φ为压缩系数.取杨氏模量E=6 MPa，体积压缩模量B=204.72 MPa，选取相应压缩系数φ=0.68[1]，可通过上述公式预测得到表征压缩模量，结果如表4所示.与表3中小形变单轴压缩测试结果相比，公式(11)可相对准确地预测边界条件①和形状因子为S3的单轴压缩测试结果；而对于试件几何特征保持不变边界条件②下进行的压缩测试结果，公式(12)的计算精度相对准确；当边界约束更改为条件③时，压缩试件形状因子对表征压缩模量的影响，只能通过公式(14)才能描述.综上所述，通过小形变力学试验及线弹性理论确定某橡胶元件力学特征的方法具有一定局限性，不仅无法获取大形变范围可能发生的非线性特征，压缩测试结果也易于受到试件尺寸和边界条件等因素影响.杨氏模量与表征压缩模量理论关系的预测公式需视情况而定.

表4 表征压缩模量预测模型和结果

3 仿真分析

本文进一步利用有限元手段采用非线性模型对大形变试验进行仿真分析，通过一组试验数据与仿真结果的比较，验证计算过程的有效性；而后通过仿真分析预测不同工况下单轴压缩应力-应变关系，与不同试件尺寸和边界条件下进行的小形变压缩试验结果进行比较，最终目的是验证大形变试验结合超弹性理论和仿真分析是大形变以及压缩为主的复杂形变橡胶元件设计-生产-优化过程最合理有效的方法.

图8所示为大形变试验仿真计算过程，其中图8a和图8b表示小形变试验仿真过程.橡胶材料均采用实体单元C3D8R，单轴压缩试验PTFE块和铁块以及平面拉伸试验的铝片均采用刚体单元R3D4.压缩试验橡胶试件与PTFE块/铁块的垂向接触属性设为“硬接触”，即当两表面间隙为零时定义为接触，接触面之间产生并传递接触应力，接触行为通过节点约束，节点之间不允许发生穿透行为；切向通过罚函数接触算法定义，由于边界条件①几乎不存在横向摩擦，因此摩擦系数设置为0时的仿真结果与试验结果能够较好吻合.同理，单轴压缩边界条件②和③的切向接触属性通过设置横向摩擦系数0.5和0.3进行模拟.平面拉伸试验铝片与橡胶元件之间的黏结通过“绑定接触”定义，接触面间隙为零，且不允许发生相对位移.橡胶材料属性采用Van der Walls模型和表1中的参数进行描述，赋予橡胶材料超弹性特征.

由图8可见，大形变试验仿真过程单轴拉伸沿x方向50 mm，最大应变量100%；单轴压缩沿z方向6 mm，压缩应变达50%.平面拉伸沿y方向约9 mm，应变量最大约为75%，该值小于测试目标100%，但大于由于铝片与试件发生脱落导致的实际最大应变量65%.图8仅示意仿真过程及加载情况，计算结果详见图4～7.图4中，单轴拉伸、平面拉伸和单轴压缩试验应力-应变曲线与实测曲线保持了较好的一致性，验证了超弹性模型和参数以及仿真过程的有效性.在此基础上，进一步仿真分析小形变单轴拉伸以及不同试件尺寸和加载边界条件下的单轴压缩试验，仿真与实测的应力-应变关系比较分析详见图5～7.由图5可知，仿真结果与单轴拉伸和压缩试验结果保持一致，由图6和图7可知，该方法还可以准确预测压缩试验对试件尺寸和边界条件的依赖性.对于边界条件②和③，试件上、下表面横向约束相对严格，此时的轴向承载过程元件内部产生两种响应应力：与简单压缩形变ε对应的均匀压缩应力σc，以及与接触表面剪切应变对应的剪切应力σs.产生剪切应变是由于接触表面的约束作用使接触表面各质点始终具有由变形后位置向初始位置恢复的倾向导致的，从而使表征压缩模量大于材料弹性模量.当横向约束力较大时，橡胶元件最大剪切应变接近于最大压缩应变；而当横向摩擦被消除时，最大剪切应变远远小于最大压缩应变，可忽略不计，试件被视为发生了纯压缩形变.综上所述，大形变力学试验结合超弹性理论和仿真分析，可有效获取橡胶材料的弹性特征参数，也可合理预测大形变状态下的非线性特性以及压缩特性易于受到元件尺寸和实际加载条件影响的特性.

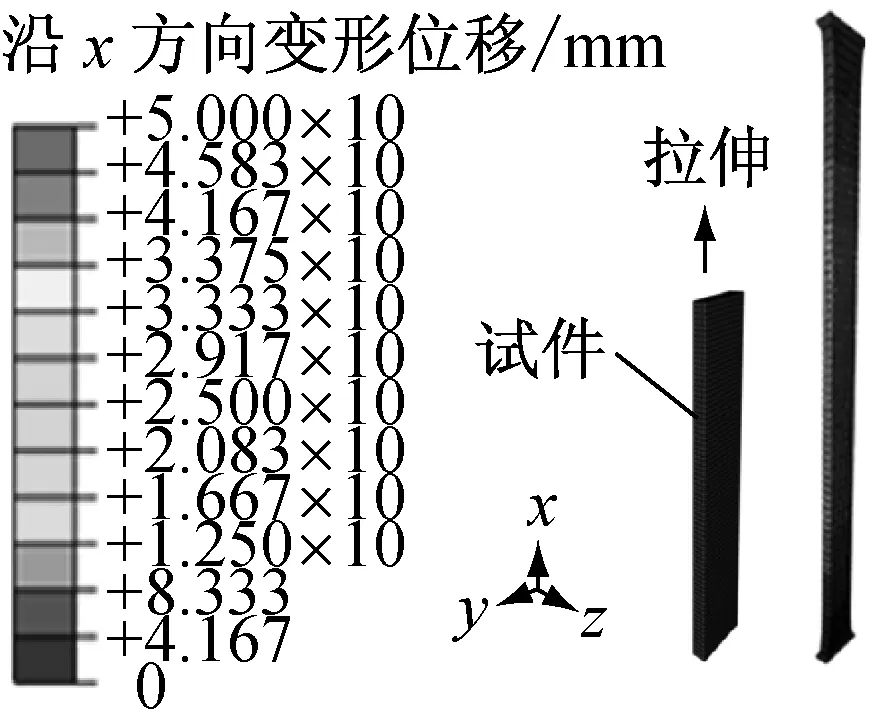
a 单轴拉伸

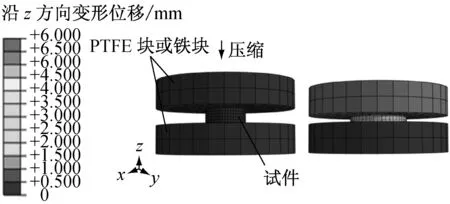
b 单轴压缩

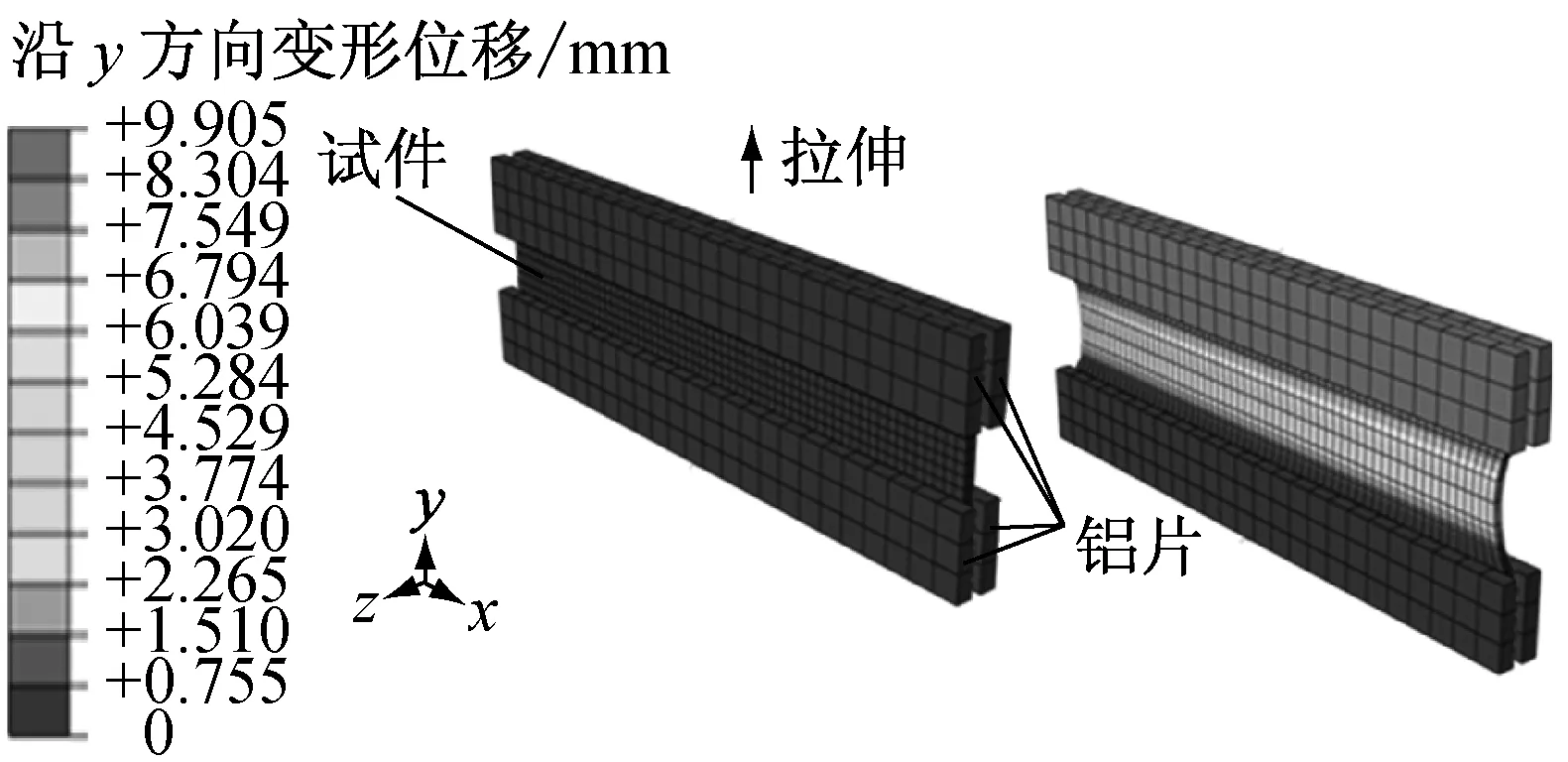
c 等轴拉伸

4 结论

橡胶材料弹性特征参数的掌握对于工程弹性体的设计和优化至关重要，根据弹性体的实际工程应用，确定其特征参数的试验手段和理论方法也有所不同.本文采用试验与数值分析相结合的方法，对一种橡胶材料进行了大、小形变试验及理论分析.试验及数值计算结果表明：

(1) 基于超弹性理论的单轴拉伸、单轴压缩和平面拉伸试验和分析结果，可相对完整地定义材料的回弹特性，定义初始剪切模量、杨氏模量、体积压缩模量和表征压缩模量，并描述大形变非线性特征.

(2) 小形变试验结合线性理论与大形变试验所确定的杨氏模量和剪切模量保持一致.

(3) 通过小形变力学试验及线弹性理论确定某橡胶元件力学特征的方法具有一定局限性，不仅无法获取大形变状态下的模量硬化现象，也无法准确预测试件尺寸和边界条件等对压缩应力-应变关系的影响规律，从而预测杨氏模量与表征压缩模量的理论关系.

综上所述，当橡胶元件以拉伸或剪切形变为主且变形量属于线性形变范围时，小形变力学试验结合线性理论即可获取材料弹性特征参数；然而当弹性体形变量较大，或者当弹性体发生以压缩为主的复杂形变时，采用大形变力学试验结合非线性模型和仿真分析才是完成弹性体测试-设计-优化的最佳方法.

[1] Gent A N.橡胶工程——如何设计橡胶配件[M].张立群,等译. 北京：化学工业出版社，2001.

Gent A N. Engineering with rubber-how to design rubber components [M]. Translated by ZHANG Liqun,etal. Beijing: Chemical Industry Press, 2001.

[2] Charlton D J, Yang J. A review of methods to characterize rubber elastic behavior for use in finite element analysis [J]. Rubber Chemistry and Technology, 1994, 67(3): 481.

[3] Miller Kurt. Testing elastomers for hyperelastic material models in finite element analysis [R]. Ann Arbor: Axel Products, Inc, 2000.

[4] Horton J M, Tupholme G E, Gover M J C. Axial loading o bond rubber blocks [J]. Journal of Applied Mechanics, 2002, 69(6), 836.

[5] Gent A N, Lindley P B. The compression of bonded rubber blocks [C]∥Proceedings of the Institution of Mechanical Engineers. London: Institution of Mechanical Engineers, 1959: 111-117.

[6] 危银涛,张文飞.橡胶悬置材料与结构特性实验[R]. 北京: 清华大学, 2010.

WEI Yintao, ZHANG Wenfei. Rubber mount material and structural characteristics experiment investigation on the material and structural characteristics of automotive suspension [R]. Beijing: Tsinghua University, 2010.

[7] Williams J G, Gamonpilas C. Using the simple compression test to determine young’s modulus, Poisson’s ratio and coulomb friction coefficient [J]. International Journal of Solis and Structures, 2008, 45(16), 4448.

[8] Day J R, Miller K A. Equibiaxial stretching of elastomeric sheets, an analytical verification of experimental technique [C]∥Abaqus 2000 User’s Conference Proceedings. Newport: Sorensen, Inc, 2000: 205-220.

[9] 胡小玲. 炭黑填充橡胶黏超弹性力学行为的宏细观研究[D]. 湘潭：湘潭大学, 2013.

HU Xiaoling. Micro- and macro- viscohyperelastic behavior of carbon black filled rubbers [D]. Xiangtan: Xiangtan University, 2013.

[10] Axel Products, Inc. Nonlinear finite element analysis of elastomers[DB/OL]. [2015-06-17]. http://www.axelproducts. com/pages/loads.html.

[11] Axel Products, Inc. Where do the “pure” and “shear” come from in the pure shear test? [DB/OL]. [2015-06-17]. http://www.axelproducts.com/pages/loads.html.

[12] Sang J L. Active, polymer-based composite material implementing simple shear [D]. [S.l.]: Texas A & M University, 2008.

[13] 3DS SIMULIA. Abaqus analysis user’s manual. Volume III: materials, Version 6.12 [DB/OL]. [2015-01-17]. http://www.material.physik.uni-goettingen.de/abaqus/v6.12/index.html.

Determination of Resilient Coefficients of Engineering Rubber Material

LIU Yan1,2, ZHANG Jimin1,2, LUO Yanyun2, LI Qiutong2

(1. School of Mechanical Engineering, Tongji University, Shanghai 201804; China; 2 Institute of Rail Transit, Tongji University, Shanghai 201804, China)

Determination of resilient coefficients of rubber material is essential to the design and optimization of elastomers in most engineering fields. Based on the nonlinear elasticity theory, a set of experiment including uniaxial tension, uniaxial compression and planar tension tests under large deformation was conducted and coefficients of a hyperelastic model were fitted. The testing data and corresponding simulation results can be used, on the one hand, to integrallty define the initial shear modulus, Young’s modulus, bulk modulus and apparent compressive modulus of present material, and on the other hand, to accurately predict the material nonlinearity and strong dependence of compressive modulus under different test conditions. Then a set of material mechanics experiment within small deformations was performed and the corresponding linear modulus were calculated. Finally, several conclusions about small and large material mechanics experiment as well as linear and nonlinear elastic theory were proposed through comparative analysis.

engineering rubber material; shear modulus; Young’s modulus; bulk modulus; apparent compressive modulus; finite element analysis

2015-09-01

国家自然科学基金(51408434,61174214)；中国博士后科学基金(1000229047)

刘 艳(1985—),女,工学博士,主要研究方向为轨道工程和固体力学.E-mail:liuyans.851010@hotmail.com

TQ332

A