直击中考——二次函数的应用

江美红

直击中考——二次函数的应用

江美红

二次函数在中考中的考点很多，经常以拉分题形式出现在卷末.下面以今年的中考题为例，让我们一起来看看中考从哪些角度考查这类题型.

一、二次函数的几何型应用

例1（2016·江苏泰州）二次函数y=x2-2x-3的图像如图1所示，若线段AB在x轴上，且AB为23个单位长度，以AB为边作等边△ABC，使点C落在该函数y轴右侧的图像上，则点C的坐标为.

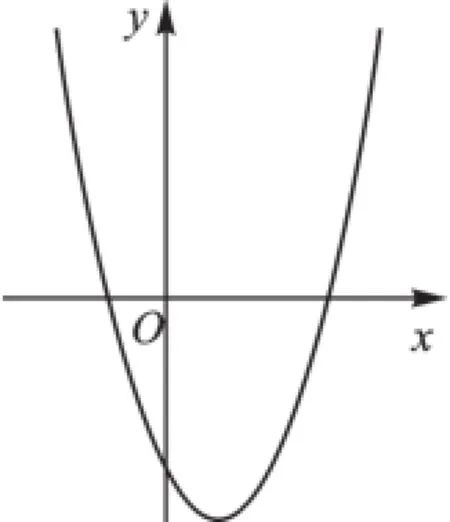
图1

【考点】等边三角形、二次函数.

【分析】由题意，点C满足两个条件，一是△ABC是等边三角形，二是点C在函数y轴右侧的图像上.设点C的坐标为（a，a2-2a-3），过点C作AB的垂线段CD，根据△ABC是等边三角形，AD=，可得CD=3，列出关于a的方程，求出a的值，得出点C的坐标.

解：如图2，过点C作CD⊥AB，垂足为D.

设点C坐标为（a，a2-2a-3），

∴CD=|a2-2a-3|.

∴|a2-2a-3|=3.

∴a2-2a-3=3，得出a=1±.

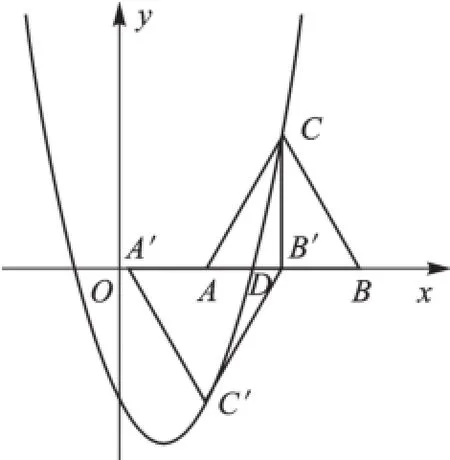
图2

或a2-2a-3=-3，得出a=0或a=2.

【总结】题中的点C满足两个条件，若先设点A的坐标，根据等边三角形的线段关系得出点C的坐标，再代入抛物线的解析式中，此种做法显得繁琐且方程难以解出，因此解题时如若遇到这种情况，不妨换种思路，先利用点C在抛物线上的条件设出点C的坐标，再结合等边三角形的知识列出方程，你会发现“柳暗花明又一村”.

二、二次函数的代数型应用

例2（2016·江苏扬州）某电商销售一款夏季时装，进价40元/件，售价110元/件，每天销售20件，每销售一件需缴纳电商平台推广费用a元（a＞0）.未来30天，这款时装将开展“每天降价1元”的夏令促销活动，即从第1天起每天的单价均比前一天降1元.通过市场调研发现，该时装单价每降1元，每天销量增加4件.在这30天内，要使每天缴纳电商平台推广费用后的利润随天数t（t为正整数）的增大而增大，a的取值范围应为_______.

【考点】利润问题、二次函数.

【分析】根据题意可以先列出第t天缴纳电商平台推广费用后的利润关于天数t的函数，再根据利润随天数的增大而增大的条件，结合二次函数的图像与性质、天数t的范围，列出关于a的不等式，求出a的取值范围.

解：由题意，第t天缴纳电商平台推广费用后一件时装的利润为（70-a-t）元，第t天时装的销量为（20+4t）件，设第t天获得的利润为y元，则y=（70-a-t）（20+4t）=-4t2+（260-4a）t+ 1400-20a.

∵此二次函数图像——抛物线的开口向下，且当0≤t≤30时，y随t的增大而增大，∴抛物线顶点的横坐标应大于或等于30，

∵a＞0，∴a的取值范围是：0＜a≤5.

【总结】此题有两大关键，一是正确列出利润y关于天数t的函数，二是结合图像及性质确定抛物线对称轴的范围.突破此两大难点，需要对知识点的熟练掌握和一定的分析问题的能力.

三、二次函数的综合型应用

例3（2016·江苏南京）图中是抛物线形拱桥，P处有一照明灯，水面OA宽4m，从O、A两处观测P处，仰角分别为α，β，且，以O为原点，OA所在直线为x轴建立直角坐标系.

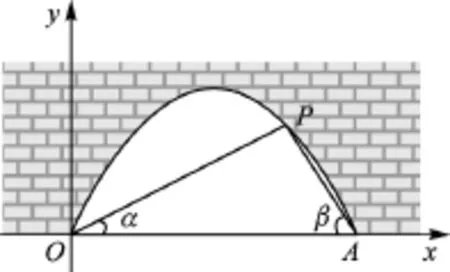
（1）求点P的坐标；

【考点】三角函数、二次函数.

【分析】（1）根据三角函数的意义，过点P作OA的垂线段PB，设PB为x，用x表示OB、 AB，由OA=4，列出方程求出x，写出点P的坐标.

（2）根据抛物线经过点O、A、P，求出抛物线的解析式，当纵坐标为1时，求出相应的两个横坐标，从而求出水面的宽度.

解：（1）如图，过点P作PB⊥OA，垂足为B.

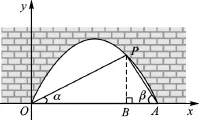
（2）设此抛物线表示的二次函数为y=ax2+ bx.由函数y=ax2+bx图像经过（4，0）、可得解得

答：水面宽度约为2.8m.

【总结】本题结合抛物线经过原点解析式的特征，运用待定系数法来求解，当然也可以用交点式（双根式）或一般式求解.其次把实际问题抽象到数学问题，把求水面的宽度转化为求点的坐标，再利用抛物线上点的坐标与距离之间的关系求出水面的宽度.此类题目若能顺利转化为数学问题，求解过程一般不会太难.

（作者单位：江苏省太仓市实验中学）