槽式太阳能集热器传热模型及性能分析

陈玉英

(兰州交通大学 环境与市政工程学院，兰州 730070)



槽式太阳能集热器传热模型及性能分析

陈玉英

(兰州交通大学 环境与市政工程学院，兰州 730070)

槽式太阳能集热器一维和二维传热数学模型是一组非线性代数方程，为改进求解的稳定性和计算精度，将槽式太阳能集热器一维和二维传热模型的求解看作有约束优化问题，建立了集热器传热过程求解的有约束优化数学模型，应用MATLAB软件优化函数fmincon进行求解。分析了传热流体入口温度及太阳能辐射热流密度变化对集热器性能的影响。采用fmincon函数求解集热器传热过程，计算速度快，计算过程稳定。分析表明，传热流体温度变化对集热器效率的影响大于太阳能辐射热流密度对集热器效率的影响。

槽式集热器；太阳能；传热；MATLAB

槽式聚焦太阳能集热器是一种高效的太阳能热利用集热器，广泛用于太阳能热力发电、物料干燥，海水淡化等领域[1-5]。槽式太阳能集热器性能涉及聚焦器、集热器的光学性质、集热器复杂的传热过程、集热器结构等着诸多方面，就其传热模型，传热性能来说，学者们对其进行了不同程度的研究。文献[6] 基于热平衡方法，建立了对吸热器直接加热的实验装置，对集热器热损失进行了研究。由于对抛物面聚焦集热器整体进行实验研究受到多方面的限制，而基于热平衡法的实验研究缺乏对包括聚光器、传热流体在内的集热器整体性能的认识，基于集热器传热模型建立与求解的数值模拟分析方法受到人们的关注[7-13]。文献[7-8]对槽式太阳能集热器建立了一维、二维稳态传热的数学模型，分别应用EES工程方程求解器及MATLAB软件符号函数solve进行了求解，文献[9-10]应用MATLAB软件非线性方程组求解函数fsolve对集热器一维稳态传热模型进行了求解。

槽式太阳能集热器一维和二维稳态传热数学模型是一组非线性代数方程，在集热器实际工作中，集热管和玻璃护管壁面温度存在一定依赖关系，这里将集热器传热数学模型的求解看做优化问题，通过集热器热平衡方程和传热方程，建立求解集热器传热过程的有约束优化数学模型，应用MATLAB软件优化工具箱函数fmincon进行求解。fmincon函数内嵌多种优化方法，可使求解过程更稳定，同时计入集热器各部分温度的依赖关系，使计算结果更合理。本文在求解传热方程的基础上，分析了部分因素对集热器性能的影响。

1 集热管传热模型

1.1 集热管一维传热模型

1.2 集热管热平衡方程

根据能量守恒原理，传热流体、吸热管和玻璃管的热平衡关系可用式(1)～(6)表示。

对于传热流体和吸热管，传热流体与吸热管内表面的对流换热量等于通过吸热管的导热量。

(1)

对于吸热管外表面，吸热管吸收的太阳辐射热量等于通过吸热管壁的导热量、吸热管外表面与玻璃管内表面的对流换热量及辐射换热量之和。

(2)

对于玻璃管内表面，玻璃管内表面与吸热管外表面通过对流和辐射交换的热量等于通过玻璃管壁的导热量。

(3)

对于玻璃管外表面，玻璃管外表面吸收的太阳辐射热量与通过玻璃管壁的导热量之和等于玻璃管外表面与周围环境的对流换热量与玻璃管外壁与天空的辐射换热量之和。

(4)

考虑到关系式(3)，式(4)又可表示为

(5)

集热管热损失为

(6)

设到达抛物面槽式集热器的太阳总辐射热量为ΦSolar，则集热器热效率为

(7)

1.3 集热管二维传热模型

在一维传热模型中，换热流体温度可以按两种方式考虑，一是取流体平均温度作为流体的整体温度，不考虑温度沿管长的变化；二是仅考虑流体进出口温度的变化，认为沿管长流体温度呈线性变化。在二维模型中，将集热管分成n段，如图3所示，在每一段的边界上温度是连续的。与一维传热模型一样，假设辐射传热热流沿管长均匀分布，且垂直于管壁表面，在每一小段上，纵向温度假设是线性的。

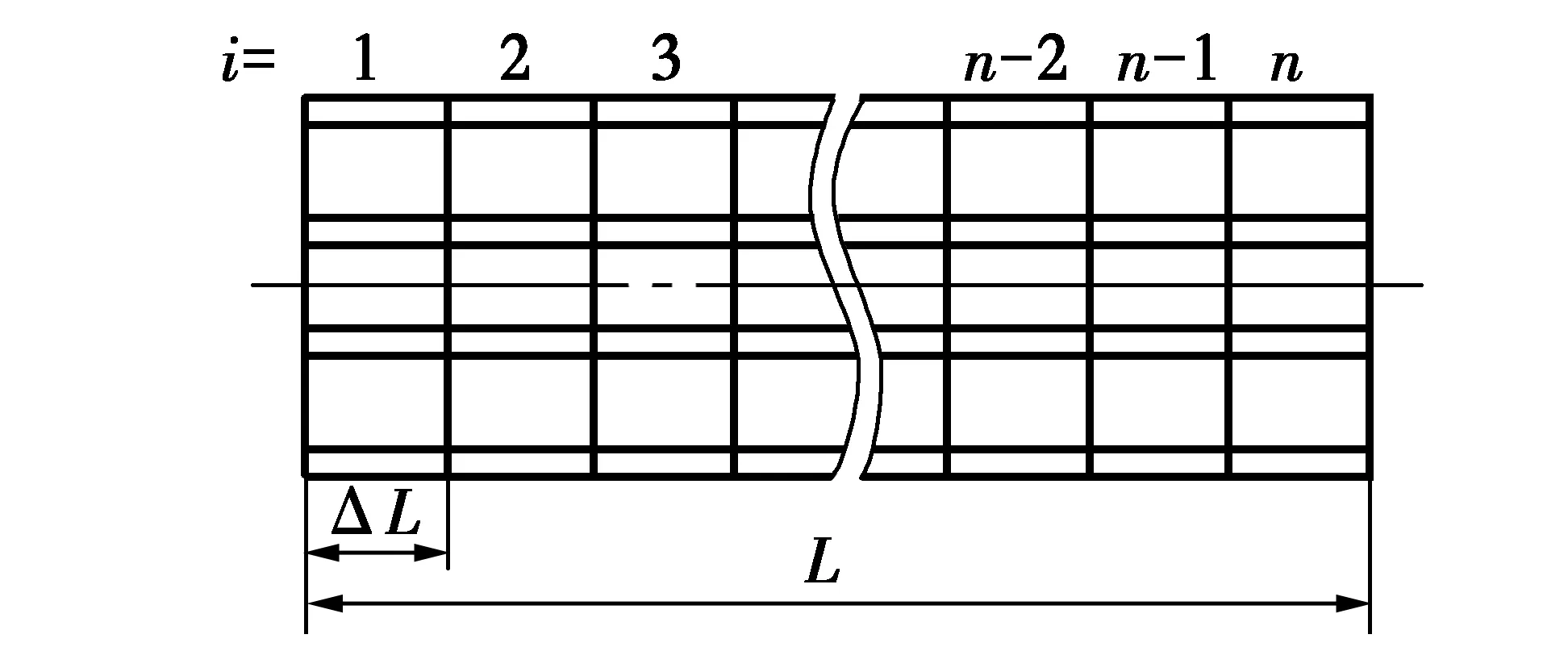
图3 集热管分段传热模型

在每一小段上，集热管不仅满足式(1)～(5)的热平衡方程，还需引入流体本身的热平衡方程

(8)

1.4 集热管传热计算

1.4.1 传热流体与吸热管之间的对流传热 由牛顿冷却公式，从吸收管内表面到传热流体的对流传热为

(9)

(10)

吸热管内对流换热努塞尔数Nud2的计算取决于传热流体流动状态。

紊流和过渡流(Red2>2 300)情况下，努塞尔数计算式为[8]

(11)

其中,f2按式(12)计算。

f2=(1.82log10(Red2)-1.64)-2

(12)

管内流体为层流(Red2<2 300)时,努塞尔数为常数，等于4.36。

1.4.2 吸热管与玻璃护管的传热 在吸热管与玻璃护管间通过对流和辐射进行换热。对于对流换热，当环形腔内压力较低(压力<133.32 Pa) 时，传热机理是分子导热，在较高压力下(压力>133.32 Pa)，传热过程是自然对流。当环形区域内压力<133.32 Pa时，对流换热系数按式(13)计算[7-8)。

(13)

b和k的表达式分别为

(14)

(15)

当环形区域内压力>133.32 Pa时，对流换热量按式(16)～(21)计算[7-8]。

(16)

(17)

(18)

(19)

(20)

(21)

1.4.3 玻璃护管与环境的对流换热 玻璃护管与外界空气的对流换热，在无风时为自然对流换热，有风时为强迫对流换热。自然对流换热时努塞尔数通过式(22)～(24)计算[7-8，14]。

(22)

(23)

(24)

式(22)～(24)中各变量含义与式(19)类似。

有风时，玻璃护管与空气的对流换热按流体横掠单管时的经验公式计算。通过吸热管及玻璃管导热计算按通过圆筒壁导热公式计算，吸热管外壁面与玻璃管内壁面的辐射换热按两无限长环形空腔辐射传热公式计算，玻璃护管外表面与天空辐射换热按无限大封闭面与内包凸表面物体辐射换热计算[13,15]。

2 集热管传热过程求解

集热管传热计算中，通常给定太阳总辐射热流密度Isolar，传热介质入口温度t1,in，环境温度t6,天空温度t7,待定参数包括传热介质出口温度t1,out,吸热管内外壁表面平均温度t2及t3，玻璃护管内外壁表面平均温度t4及t5，共5个未知量，可通过式(1)～(4)、式(8)以及相应的传热公式来进行求解。由于辐射热流量与温度的4次方成正比，因此，引入传热计算式后，热平衡方程是关于温度的非线性代数方程。文献[7]应用工程方程求解器(EES)来求解这一组代数方程。MATLAB软件有丰富的数学库函数及优化工具箱函数，给非线性代数方程组的求解带来很大方便，文献[9-10]分别应用MATLAB软件提供的代数方程组符号求解函数solve及fsolve来求解这一组代数方程。这里采用MATLAB软件提供的求解约束优化问题的函数fmincon来求解这一组非线性代数方程[16]。与solve及fsolve函数相比，采用约束优化函数fmincon进行求解时程序设计简单，计算速度更快，稳定性更好。

由式(1)～(4)及式(8)构造的优化问题数学模型为

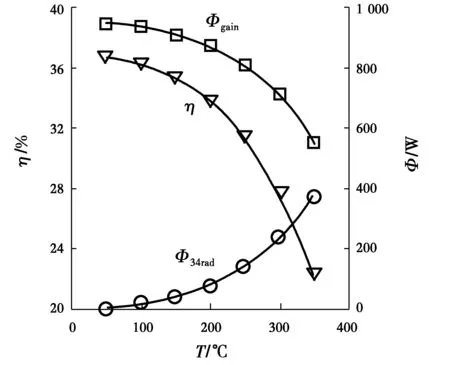
s.t. t4

t5

t6

(24)

设计变量x=[t2,t3,t4,t5,t1,out]。

方程eqi(i=1,2,...,5)通过对式(1)～(4)及式(8)移项，使方程右端项为零得到。

3 计算结果及分析

3.1 计算参数

算例采用文献[8]给出的集热管参数，各部分结构参数如表1所示。

表1 集热器结构参数 m

取传热流体入口温度t1,in=45.3 ℃,传热流体体积流量V=0.226 8 m3/h，外界风速u5=3.8 m/s,外界空气温度t6=26.6 ℃，天空温度t7=t6-8 ℃。

3.2 计算结果与实测结果比较

传热计算分别按一维和二维模型进行，对于二维传热模型，将集热管分为12段。在太阳辐射热流密度为均匀的情况下，一维和二维传热模型结果相同。模拟计算结果与文献[8]实验结果如表2所示。

表2 集热器传热计算值与实验结果比较

由表2可知，计算值与实测值相对误差最大值为1.64%，说明用MATLAB软件的优化函数fmincon求解集热器传热过程有较好的精度。

3.3 传热流体入口温度对集热器性能的影响

传热流体体积流量V=0.226 8 m3/h，环境温度t6=26.6 ℃，外界风速u5=3.8 m/s,到达集热槽开口面单位长度的太阳辐射热量I′=758 W/m时，传热流体入口温度与集热器热效率关系曲线如图4所示。

图4 传热流体入口温度与集热器效率关系曲线

从图4可以看出，随着吸热管传热流体入口温度的增加，流体从太阳辐射吸收的热量Φgain呈下降趋势，且流体入口温度越高，下降的程度越明显，集热器效率随传热流体温度的增加也呈下降趋势。这是因为，随着传热流体入口温度的增加，吸热管管壁温度增加，在外界气温和风速不变的情况下，玻璃套管壁面温度增加有限，使得吸热管与玻璃护管间辐射换热量Φ34rad增加，热损失增加，因此，集热器效率下降。在吸热管与玻璃护管环形空腔内真空度较高的情况下，吸热管与玻璃护管间对量换热量较少，热损失主要由辐射散热产生。吸热管与玻璃护管间辐射换热量通过玻璃护管的导热及护管外表面与环境的对流换热和辐射换热散出。

3.4 太阳辐射热流密度对集热器性的能的影响

传热流体体积流量V=0.226 8 m3/h，传热流体入口温度tin=200 ℃，环境温度t6=26.6 ℃，外界风速u5=3.8 m/s时，太阳辐射热流密度与集热器热效率关系曲线如图5示。

图5 太阳辐射热流密度与集热器效率关系曲线

随着太阳辐射热流密度的增加，集热器效率呈增加的趋势，由于散热损失(如玻璃护管外壁与环境的对流换热量Φ56conv)也呈增加的趋势，因此，集热器效率随太阳辐射热流密度的增加其增加的幅度较平缓。传热流体温度变化对集热器效率的影响大于太阳辐射对集热器效率的影响。

4 结 论

在建立槽式集热器一维和二维稳态传热模型的基础上，应用MATLAB软件优化工具箱函数fmincon对热平衡方程和传热方程进行了求解，并对部分因素对集热管性能的影响进行了分析，通过模拟计算和分析可得出以下结论。

1)将集热器传热模型按优化问题进行求解可以加快求解速度，提高求解的稳定性。

2)随传热流体入口温度的增加，集热器效率显著下降；随太阳辐射热流密度的增加，集热器效率呈平稳增加的趋势。

3)在吸热管与玻璃护管环形空腔内真空度较高的情况下，吸热管的散热主要是辐射换热；集热管热效率对传热流体温度变化的影响要高于太阳辐射热流密度变化对集热器效率的影响。

附：符号说明

[1] 黄素逸, 黄树红, 许国良. 太阳能热发电原理及技术[M]. 北京: 中国电力出版社，2012.

HUANG S Y, HHUANG S H, XU G L. Principle and technology of solar thermal power generation[M]. Beijing: China Electric Power Press，2012.(in Chinese)

[2] 王金平，王军，张耀明，等. 槽式太阳能聚光集热器传热特性分析[J]. 农业工程学报，2015，31(7): 185-192.

WANG J P, WANG J, ZHANG Y M,et al. analysis of heat transfer characteristics for parabolic trough solar collector[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015，31(7): 185-192. (in Chinese)

[3] 徐伟, 杨帆, 刘静静,等. 槽式抛物面太阳能热发电系统发展现状与探讨[J]. 发电设备，2015，21(1): 74-78.

XU W, YANG F, LIU J J, et al. Review and discussion on parabolic trough solar power systems[J], Power Equipment, 2015，21(1) : 74-78. (in Chinese)

[4] 杨敏林, 杨晓西, 林汝谋, 等. 太阳能热发电技术与系统[J]. 热能动力工程, 2008, 23(3): 221-228.

YANG M L, YANG X X, LIN R M. Solar energy-based thermal power generation technologies and their systems[J]. Journal of Engineering for Thermal Energy & Power, 2008, 23(3): 221-228.(in Chinese)

[5] FERNANDEZ-GARC A, ZARZA E, VALENZUELA L,et al. Parabolic-trough solar collectors and their applications[J]. Renewable and Sustainable Energy Reviews, 2010,14: 1695-1721.

[6] 熊亚选, 吴玉庭, 马重芳,等. 槽式太阳能聚光集热器光热性能初步实验研究[J]. 太阳能学报, 2012, 33(12) : 2087-2092.

XIONG Y X,WU Y T ,MA C F,et al. Preliminary experiment study on the thermal performance of a parabolic trough collector[J]. Acta Energiae Solaris Sinica, 2012, 33(12) : 2087-2092.(in Chinese)

[7] FORRISTAL R. Heat transfer analysis and modeling of a parabolic trough solar receiver implemented in engineering equation solver[R]. Colorado: National Renewable Energy Laboratory, 2003.

[8] ALFELLAG, MOHANAD ABDULAZEEZ ABDULRAHEEM. Modeling and experimental investigation of parabolic trough solar collector[D]. Florida: Embry-Riddle Aeronautical University, 2014 .

[9] 杨润, 李斌. 基于MATLAB 的抛物槽式太阳能集热器集热管一维稳态模型[J]. 可再生能源，2008,26(4)：6-9.

YANG R, LI B. The calculation of the 1-D steady-state model of the parabolic trough solar absorber pipe based on MATLAB [J]. Renewable Energy Resources, 2008,26(4)：6-9.(in Chinese)

[10] 韦彪, 朱天宇, 刘德有. 槽式DSG太阳能集热系统模拟分析[J]. 工程热物理学报，2012,33(3): 473-476.

WEI B, ZHU T Y, LIU D Y. Simulation of heat transfer for parabolic trough DSG solar collectors [J]. Journal of Engineering Thermophysics, 2012, 33(3):473-476 .(in Chinese)

[11] WANG K， HE Y L， CHENG Z D. A design method and numerical study for a new type parabolic trough solar collector with uniform solar flux distribution [J]. Science China Technological Sciences, 2014, 57(3):531-540.

[12] M-C. EL JAI，F-Z. CHALQI. A modified model for parabolic trough solar receiver [J]. American Journal of Engineering Research, 2013,2(5):200-211.

[13] 周传文. 槽式太阳集热器热性能研究[D]. 北京：华北电力大学，2013.

ZHOU C W. Thermal performance analysis of trough solar collector[D]. Beijing: North China Electric Power University, 2013.(in Chinese)

[14] WU Z Y, LI S D, YUAN G F,et al. Three-dimensional numerical study of heat transfer characteristics of parabolic trough receiver [J]. Applied Energy, 2014,113: 902-911.

[15] 杨世铭，陶文铨. 传热学[M].4版. 北京：高等教育出版社，2006 .

YANG S M, TAO W Q. Heat transfer [M].4th Edition Beijing: Higher Education Press, 2006.(in Chinese)

[16] 张永恒. 工程优化设计与MATLAB实现[M]. 北京：清华大学出版社，2011.

ZHANG Y H. Engineering optimization design with MATLAB implementation[M]. Beijing: Tsinghua University Press, 2011.(in Chinese)

(编辑 胡玲)

Performance analysis and heat transfer model building of parabolic trough solar collector

Chen Yuying

(School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou 730070, P.R. China)

One-dimensional and two-dimensional heat transfer mathematic model of the parabolic trough solar collector are a set of nonlinear algebra equations. In order to promote the stability and accuracy of the solution , the calculation of the heat transfer model of the parabolic trough solar energy collector is treated as constrained optimum problem, the energy conservation equations and heat transfer equations are converted into optimization model, the optimization model is solved by using fmincon function in MATLAB optimization tool box. The influences of heat transfer fluid inlet temperature and solar radiation flux to heat collector coefficient are analyzed. The solution of heat collector heat transfer process is faster and more stable by using fmincon function. Results show that the variation of heat transfer fluid inlet temperature plays more important role on heat collector coefficient than that of the variation of solar radiation flux.

parabolic trough collector; solar energy; heat transfer; MATLAB

2016-01-10

陈玉英(1976-)，女，主要从事强化传热研究，(E-mail)chenyy@mail.lzjtu.cn。

TK512

A

1674-4764(2016)04-0053-06

10.11835/j.issn.1674-4764.2016.04.009

Received:2016-01-10

Author brief：Chen Yuying(1976-)，main research interest:enhancement of heat transfer，(E-mail)chenyy@mail.lzjtu.cn.