高等数学在公务员考试中的应用

刘 辉

(黑龙江财经学院 基础部，黑龙江 哈尔滨 150025)



高等数学在公务员考试中的应用

刘 辉

(黑龙江财经学院 基础部，黑龙江 哈尔滨 150025)

近几年的公务员考试中，有部分考题虽然利用初等数学的知识可以完成，但是利用高等数学、线性代数以及概率论与数理统计解决会提高计算准确度，同时节省时间，收到事半功倍的效果。针对近几年的公务员考试中的个别考题，提出解决方案，总结高等数学在各个问题中的应用。

极值点；容斥原理；古典概型；行最简形；高等数学；公务员考试

近几年，公务员考试的热情持续不断，报考人数逐渐增加，在如此激烈的竞争局面下，考生想脱颖而出，就需要有行之有效的备考方案。针对现状，本文就高等数学在公务员考试中的应用情况加以总结，以期为考生提供参考。

1 微积分在公务员考试最值问题中的应用

公务员考试中，最常用的是二次函数法，即二次函数

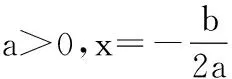
各辅导机构主张学员采用该方法解决最值问题，而实际上二次函数法只能解决二次函数的最值问题，解决的问题范围较小。

在微积分中，对于函数y=a1xn+a2n-1+…+anx+an+1，经常使用求导法求最值。当y′=a1nxn-1+a2(n-1)xn-2+…+an=0时，求得的点利用极值判别法找得相应的最值点x，并代入原式可以得到y的最值。

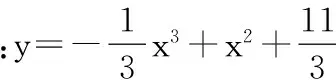
解：令y′=-x2+2x=0⟹x=0或x=2

由于产量x>0，因此x=2必为所求，

即x=2时，净利润取得最大值，且最大值为50万元。

例2：(2009年江苏)某商店商品，单价为75元，可卖500个，单价每涨1元，就会少卖20个，为了使销售量大，那么单价可定为多少元？

解：设定价为x元

则收入函数为L(x)=x[500-20(x-75)]=-20x2+2000x

令L′(x)=-40x+2000=0⟹x=50

L″(x)=-40<0，则x=50为L(x)的极大值点，且为唯一极值点，即为L(x)的最大值点。

利用导数求解函数的最值问题，方便快捷，比传统的二次函数求解最值问题适用范围更广，同时注意如果仅求解最值点，就仅求出导数为零的驻点即可；如需求解最值时，才需要求出相应函数的函数值。

2 概率在公务员考试中的应用

2.1 容斥原理

容斥原理是在不考虑重叠的情况下，先将所有对象的数目相加，然后再减去重复的部分，从而使得计算结果既无遗漏又无重复。一般情况下，涉及求解多集合元素个数的题目都需要用到容斥原理。容斥原理问题的求解方法有公式法和文氏图法。

(1)公式法

①两个集合：︱A∪B︱=︱A︱+︱B︱-︱A∩B︱

②三个集合：︱A∪B∪C︱=︱A︱+︱B︱+︱C︱-︱A∩B︱-︱B∩C︱-︱C∩A︱+︱A∩B∩C︱

③满足条件1的个数+满足条件2的个数-两者都满足的个数=总个数-两者都不满足的个数。

(2)文氏图(集合关系图)法

例1：(2006年国考一卷第42题)现有50名学生都做物理、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都做错的有4人，则两种实验都做对的有( )。

A.27人B.25人C.19人D.10人

解：40+31-x=46

解得x=25

例2：(2014年国考)对39种食物中是否含有甲、乙、丙三种维生素进行调查，结果如下：含甲的有17种，含乙的有18种，含丙的有15种，含甲、乙的有7种，含甲、丙的有6种，含乙、丙的有9种，三种维生素都不含的有7种，则三种维生素都含的有多少种？

解：17+18+15-7-6-9+x=39-7⟹x=4

例3：(云南省2008年事业单位招录考试)外国学校有英语、法语、日语教师共27人，其中只能教英语的有8人，只能教日语的有6人，能教英、日语的有5人，能教法、日语的有3人，能教英、法语的有4人，三种都能教的有2人，则只能教法语的有多少人？

解：

27-8-6-3-5=5

考生在遇到需要利用容斥原理解决问题时，最好用的方法就是作图法，简单有效，比利用公式计算相对要直观。

2.2 古典概型求概率在公务员试题中的应用

在公务员考试试题中，主要应用的是概率论中的古典概型的概率求解问题。

古典概型又称为等可能概型，需要具备如下特点：

(1)样本空间中含有有限个基本事件；

(2)样本空间中每个基本事件出现的可能性相同。

定义1：随机试验为古典概型，若样本空间中含有n个基本事件，随机事件A中含有k个基本事件，则随机事件A发生的概率为

例1：(2014年西藏)某商店举行店庆活动，顾客消费达到一定数量后，可以在4件赠品中随机选取2件不同的赠品，任意两位顾客所选赠品中，恰有1件品种相同的概率是多少？

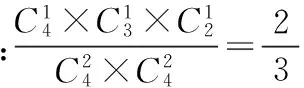
例2：(2013年江西)有甲、乙两只盒子，甲盒装有2个黑球、4个红球，乙盒装有4个黑球、3个红球， 若从甲乙两个盒

中任取两球互换后，甲盒中恰有4个红球的概率是多少？

公务员考试中遇到的概率问题，除了一些固定比赛配对问题外，主要应用的就是古典概型求概率方法，考生在做题时，主要掌握两个问题，一是试验发生的所有可能，二是所求问题的所有可能。

2.3 矩阵在公务员试题中的应用

例1：(2015年国考)甲、乙、丙三种货物，如果购买甲3件，乙7件，丙1件共需3.15元；如果购买甲4件，乙10件，丙1件共需4.20元；那么购买甲、乙、丙各1件共需多少钱？

解：设甲、乙、丙的单价分别为x,y,z元，则根据题意

因此购买甲、乙、丙各1件共需1.05元。

公务员考试过程中，如遇到解方程问题，部分考生可能会放弃。由于公务员考试的考题，用一般方法很难解出正确答案，而且还会浪费大量的时间，因此矩阵法解方程组会相应弥补这些问题，可以利用有限的时间解决问题。

近几年公务员考试的考题越来越难，主要的考点也越来越集中，主要为方程问题、行程问题、概率问题以及图形问题，而高等数学在讨论方程、概率问题时都有着明显的优势，不仅能准确地求解，同时能节省大量的考试时间。

[1]李永新.公务员考试历年真题[M].北京：人民日报出版社，2013.

[2]李允，侯嫚丹.概率论与数理统计[M].哈尔滨：哈尔滨工业大学出版社，2011.

[3]李允，吴海燕.线性代数[M].哈尔滨：哈尔滨工业大学出版社，2011.

责任编辑：富春凯

10.3969/j.issn.1674-6341.2016.06.046

2016-10-10

黑龙江省高等学校教改工程项目“本科院校向职业教育转型背景下的高等数学课程教学方法的思考”(GJD1215031)

刘辉(1982—)，女，黑龙江大庆人，硕士，副教授。研究方向：不动点。

G642

A

1674-6341(2016)06-0111-02