减小桨叶载荷的风电独立变桨优化控制模型

兰 飞，杨 萌，王哲豪，蒋 星

（广西大学电气工程学院，南宁 530004）

减小桨叶载荷的风电独立变桨优化控制模型

兰 飞，杨 萌，王哲豪，蒋 星

（广西大学电气工程学院，南宁 530004）

针对超额定风速下运行的变速变桨风电机组，研究在维持功率额定的条件下，如何减小风剪切效应所引起的不平衡载荷，从而延长风机寿命。首先依据空气动力学原理，以不平衡载荷最小为优化目标，保证输出功率与额定功率的偏差在一定范围内为约束条件，建立载荷优化模型；然后采用非线性最小二乘法，以统一变桨距角为初值，优化计算得到3个桨叶对应的最优桨距角，以该角度为参考值分别进行独立变桨距控制。仿真结果表明，与传统变桨距控制方法相比，所提模型在保证功率维持在额定值附近的前提下，大幅度减少了不平衡载荷，且避免了频繁变桨。

最优独立变桨距控制；载荷优化；风剪切效应；统一变桨距控制；不平衡载荷

风力发电技术是可再生能源中技术最成熟、最具有开发条件和商业化发展前景的发电方式之一。变桨距控制技术提高了风电机组在高风速下的发电效率，其代替定桨距风力发电机组在市场中占据了主导地位[1-4]。变桨距技术主要有2种：统一变桨距控制CPC（collective pitch control）和独立变桨距控制IPC（individual pitch control）[5]。目前CPC控制在工程应用较为广泛，其以轮毂高度处的风速作为所有桨叶的统一参考风速，风力发电机组的每个叶片在接收变桨距执行器送来的命令后变化相同的桨距角[6-7]。随着风电机组容量不断增大，桨叶长度越来越大，桨叶上的实时风速随高度的变化也越明显，即风剪切效应更显著，从而导致了同一时刻2个桨叶或者3个桨叶之间的实时风速之差较大。采用CPC控制将出现桨叶间严重的受力不平衡问题，大大降低风机的寿命。因此，大容量风电机组宜采用IPC控制方法，即3个桨叶以对应的实时风速为参考风速，分别由独立的变桨执行机构独立调节桨距角，从而有效减小不平衡载荷，延长风机寿命[8-9]。

为减小风剪切效应带来的不平衡载荷问题，国内外学者大多采用IPC方法进行控制[9-12]。目前针对该问题研究较多的是基于方位角权系数的独立变桨距控制IPCW（individual pitch control based on weight）。文献[10-11]分别采用IPCW与前馈补偿控制、动态加权模糊控制方法相结合的算法，但权系数以及隶属度函数都引入了一定的人为因素；文献[12]通过坐标变换实现载荷的d、q轴解耦，进行加入前馈滤波的PI控制，但该方法对载荷的测量要求较高，且可能存在延时性；文献[13]以攻角、相对速度等为测量信号，并在此基础进行IPC初值的设定，然而攻角的变化幅度虽小，但对载荷影响作用较大，准确地设定初值难度较大。以上对于独立变桨距控制方法的研究，都是人为进行IPC初值设定。这些方法在权系数的选取或者是测量上有一些缺陷，导致IPC初值产生较大的偏差，进而影响控制精度和速度以及对不平衡载荷的抑制效果。

本文从载荷的角度出发，考虑风剪切影响下的桨叶实时风速，采用基于载荷优化模型的独立变桨距控制IPCLO（individual pitch control based on the load optimization）方法，有效地减小了不平衡载荷，且避免了变桨距机构的频繁动作。

1 独立变桨距控制

1.1 变桨距控制模型

变桨距控制模型包括风机模型和变桨距机构模型。

当自然风轴向流过风轮时，风轮从风能中捕获的气动功率和气动转矩[14]分别为

式中：Pr为气动功率，即风轮吸收风能的实际功率；Tr为风轮的启动转矩；ρ为空气密度；CP为风能利用系数；CT为气动转矩系数；v1为来流风速；Cp（λ，β）= λCT(λ,β)，β为桨距角，R为风轮半径，λ为叶尖速比，即桨叶尖部的线速度和风速之比，表达式为

式中：Ω为风轮转动角速度；B为叶片个数。

风能利用系数CP代表风轮从风能中吸收功率的能力，可以近似表示为

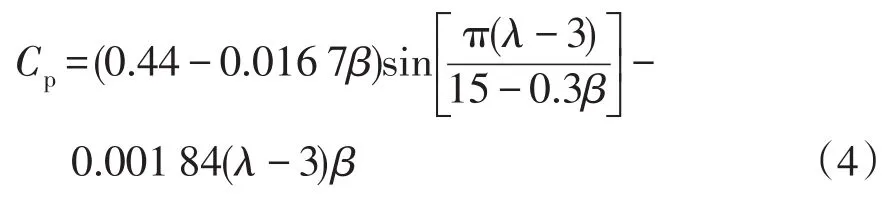
大型风电机组的变桨距系统普遍采用液压驱动系统。然而液压系统具有时滞特性，所以变桨距系统一般采用带有迟延的一阶惯性环节来模拟，其传递函数可表示为

式中：Tβ为时间常数；βr为桨距角设定值；τ为迟延时间。

1.2 独立变桨距控制

图1为CPC的控制框图，该CPC方法较为简单，通过采用不同控制器可实现输出功率的恒定。本文采用工程中常用的PID控制器对风机进行CPC控制，并在此基础上设计了IPCLO控制，其框图如图2所示。

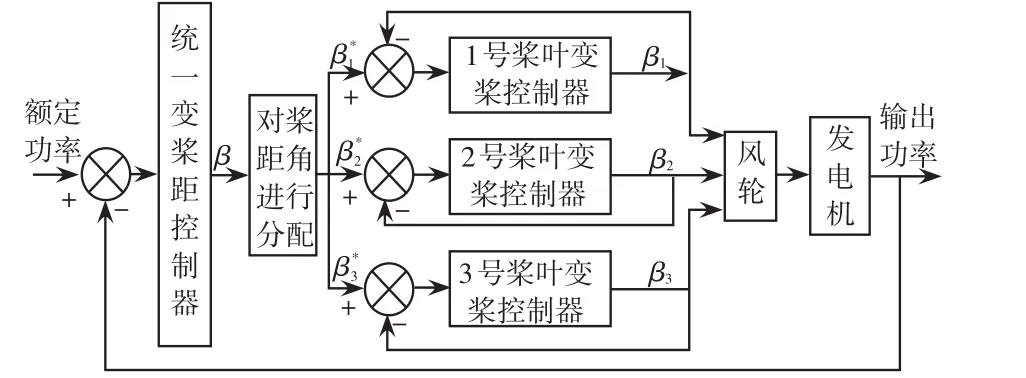
图1 CPC框图Fig.1 Block diagram of CPC

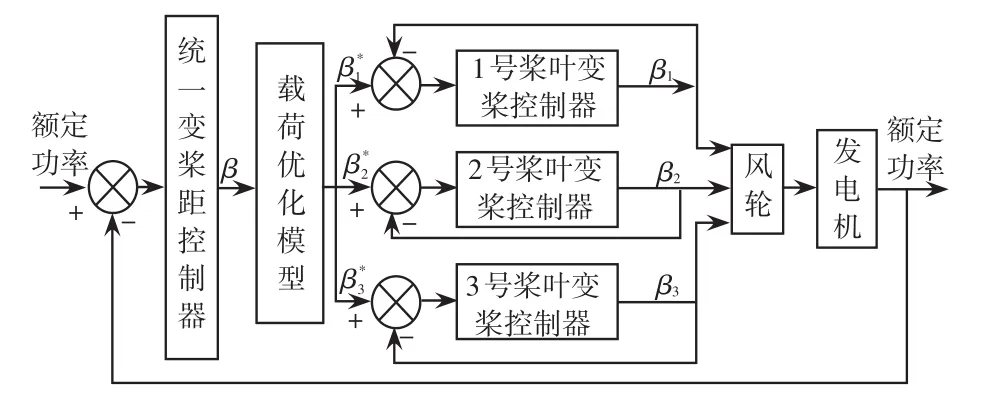
图2 IPCLO框图Fig.2 Block diagram of IPCLO

统一变桨距控制通过对输出实际功率与额定功率的偏差进行调整得到统一变桨距角β，然后以β为初值根据载荷优化模型计算得到3个桨叶对应的独立变桨距控制角β*1、β*2、β*3，从而依据图2进行IPCLO控制。

2 基于载荷优化模型的独立变桨距控制

2.1 载荷的计算模型

风机主要是通过叶片捕获风能，所以叶片是风机主要受力元件，轮毂等其他部件受力都与叶片受力有关[15]。叶片上的空气动力载荷根据动量-叶素理论计算，可得合成风速v0时桨叶摆振方向的载荷Mxb[16]，即

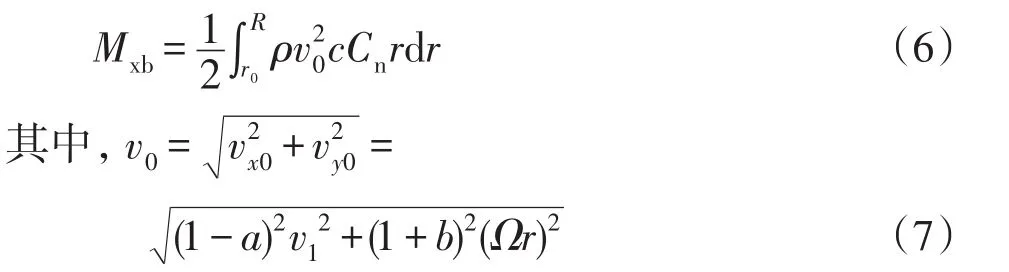
式中：c为弦长；Cn为法向力系数；r为叶素距叶根的长度；r0为用于微分计算的初始值；v0为合成气流速度；vx0、vy0分别为风轮旋转平面的垂直和平行分量气流速度；a、b分别为轴向和周向诱导因子，则有

式中：Cl和Cd通过查翼型表得到，Cl为升力系数，Cd为阻力系数；ϕ为入流角。

2.2 载荷优化模型

依据空气动力学原理计算出桨叶载荷与桨距角的函数关系，载荷优化问题就可以转换为函数求最优解的问题。令叶片间空气动力载荷差最小为目标函数，同时为了维持功率在额定值附近，桨距角和功率需作为约束条件。

IPCLO以减小不平衡载荷为目标，依据载荷计算公式（6），则载荷优化目标函数设计为

式中：βmin、βmax分别为最小、最大风速对应的统一变桨距角；P、P′分别为最小、最大风速对应的平均功率；Cn=f(β)通过Matlab对数据进行拟合得到，目标函数就可以转换为桨距角βi与实时风速之间的关系。

式（13）与风速的平方有关，可以认为是非线性最小二乘问题，应用Matlab中的lsqnonlin函数可以解决该问题。

2.3 载荷优化变桨距控制

由于方位角与对应桨叶的实时风速的对应关系，本文通过对方位角进行划分，把实时风速划分为多个区域，并对各区域采用IPCLO控制方法[10]。划分区域的依据为：桨叶间的最大风速差和桨叶的风速最大，分别进行IPCLO控制，以保证桨叶之间的不平衡载荷较小，同时各个桨叶的载荷也较小。

如图2所示，该方法以统一变桨距时的桨距角为参考值，依据各个桨叶所处区域进行优化计算，其余区域均以统一变桨距角进行变桨，以保证变桨距机构较少动作，具体仿真流程[17-18]如图3所示。以方位角0°～30°为例，该区域2号桨叶与3号桨叶的风速差最大，对应的不平衡载荷也较大。为了避免变桨距机构频繁动作，该区域2号和3号桨叶通过计算载荷优化模型得到最优桨距角，1号桨叶仍使用统一变桨距角。因此，2号和3号桨叶对应的最优桨距角分别为 β*2和 β*3；1号桨叶桨距角仍为统一变桨距角β，即 β*1=β，由此进行IPCLO控制并得到对应的载荷和功率。

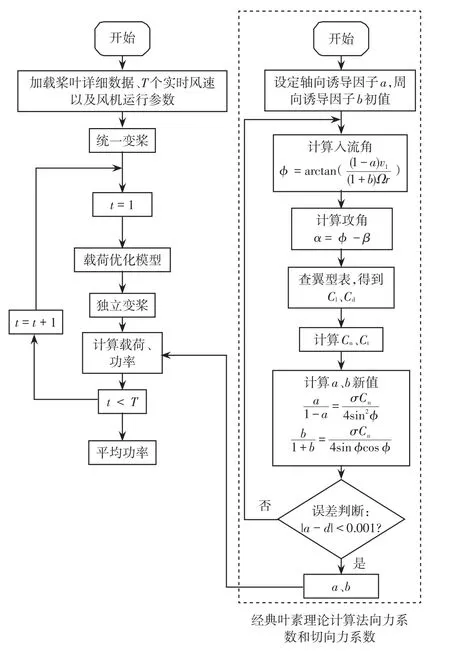
图3 仿真流程Fig.3 Flow chart of simulation

2.4 考虑风剪切效应的风速模拟

影响风速变化的因素有很多，但其中影响较大的是风剪切效应[19]——竖直方向上风速随高度的变化，高度越高，风速越大，其物理模型如图4所示。

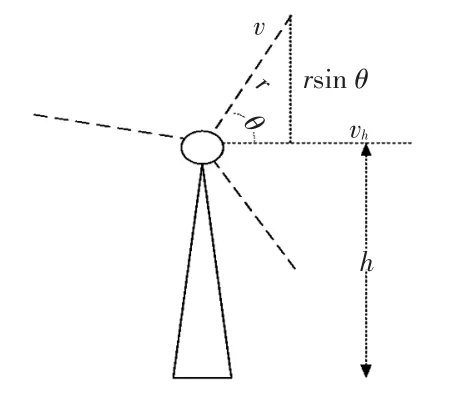
图4 风剪切效应Fig.4 Wind shear effect

风剪切时风速计算模型[20]为式中：θ为桨叶与水平面的夹角，即方位角，以轮毂处为0°，并取逆时针方向为正，顺时针方向为负；vh为轮毂离地面高度h处的风速；r为桨叶半径；∂为风剪切系数，与风轮所处环境有关，约为0.3。

以轮毂风速vh=15 m/s为例，绘制了一个风轮旋转周期下3个桨叶的实时风速，分别用1号桨叶、2号桨叶和3号桨叶来描述3个桨叶（下同），并用不同形状表示，如图5所示。桨叶间方位角互差均为120°，横轴为1号桨叶对应的方位角，纵轴为对应的实时风速。由图可知最高风速高达17.2 m/s，最低风速低至11.5 m/s，下文的算例仿真也是在该风速下进行的。

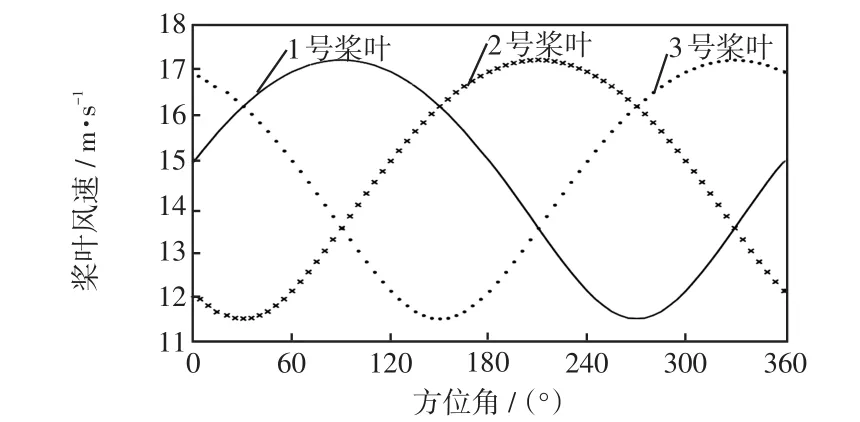
图5 受风剪切影响下的3个桨叶风速Fig.5 Wind speeds of three blades affected by wind shear effect

3 算例仿真

本文以Nordtank公司生产的NTK500/41型风机为例，对IPCLO进行了仿真。风机主要参数如下：额定功率为500 kW，转速为27.1 r/min，空气密度为1.225 kg/m3，叶片数3个，轮毂高度为35.0 m，切入风速为4 m/s，额定风速为13 m/s，切出风速为25 m/s。桨叶具体描述见表1。

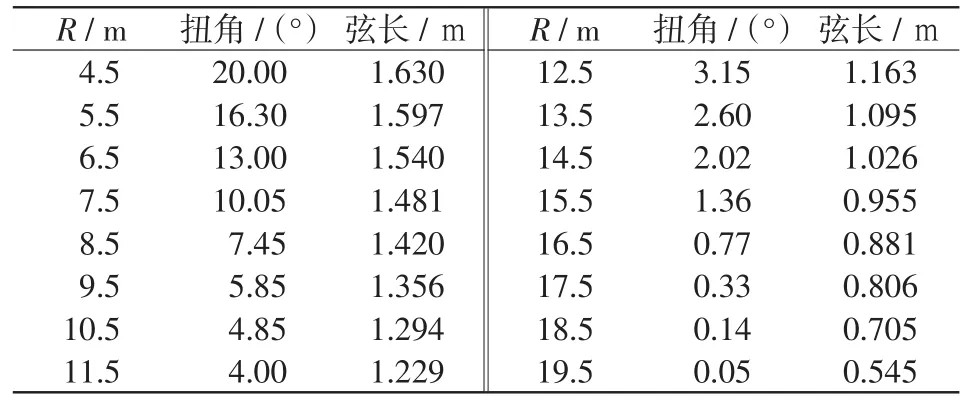
表1 桨叶具体描述Tab.1 Detailed descriptions of blade

3.1 CPC仿真结果

输入风速如图6所示，在5 s时轮毂风速从11 m/s阶跃到15 m/s。统一变桨距调整角度为6°时，功率达到500 kW，基本维持在功率附近，如图7所示。不同方位角下3个桨叶的载荷如图8所示。由图8可知，经过一个旋转周期，CPC的不平衡载荷高达5 400 N·m，且每个桨叶的载荷幅值高达12 000 N·m以上，载荷波动较大。

图6 11 m/s到15 m/s的阶跃风速Fig.6 Step wind speed from 11 m/s to 15 m/s

图7 CPC的桨距角与功率Fig.7 Pitch and power of CPC

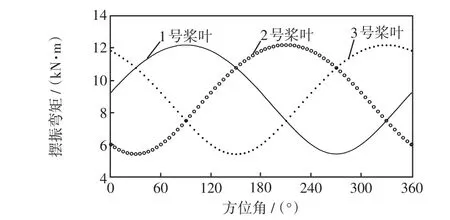
图8 不同方位角下3个桨叶的载荷Fig.8 Load of three blades at different azimuth angles

3.2 CPC与IPCW仿真对比

依据文献[18]，对统一变桨距角进行权系数分配，得到1号桨叶IPCW方法的仿真结果，并与CPC方法进行对比，对比结果如图9所示。

图9（a）为一个风轮旋转周期下的IPCW与CPC的平均功率分别为518 kW和468 kW，由图可知IP⁃CW对功率的影响并不大；图9（b）为上述2种方法在一个旋转周期下对应的载荷，相差并不大；图9（c）为2种方法对应的桨距角变化曲线，IPCW相比CPC进行了桨距角的多次调节。由图可知，IPCW相比CPC在进行多次桨距角调节的同时，并没有减小载荷也没有很好地解决不平衡载荷较大的问题。

3.3 IPCLO仿真结果

载荷和给定风速下桨叶的实时风速都是随着方位角周期变化的，因此，以1号桨叶为例，即可说明所有桨叶所受载荷、输出功率以及桨距角的变化。在30°～90°范围内，1号桨叶与2号桨叶载荷之差（不平衡载荷）最大，因此对1号桨叶和2号桨叶进行载荷优化计算，其初值分别设定为6.8°和5.6°。依据载荷优化模型计算得到的桨距角和对应的桨叶载荷如图10所示，载荷幅值不足11 000 N·m，相比图9（b）中载荷显著减小；最大不平衡载荷从5 400 N·m减小到了4 500 N·m，减小了16.7%；特别地，在方位角为90°处，不平衡载荷从4 700 N·m减小到1 900 N·m。另外，对每个桨叶来说载荷波动范围大大减小，受力相对更均匀。对应3个桨叶的输出功率如图11所示，均在允许范围内。

图9 CPC与IPCW的功率、载荷以及桨距角Fig.9 Power，load and pitch angle of CPC and IPCW

图10 载荷优化模型下的载荷与桨距角Fig.10 Load and pitch angle obtained by load optimization model

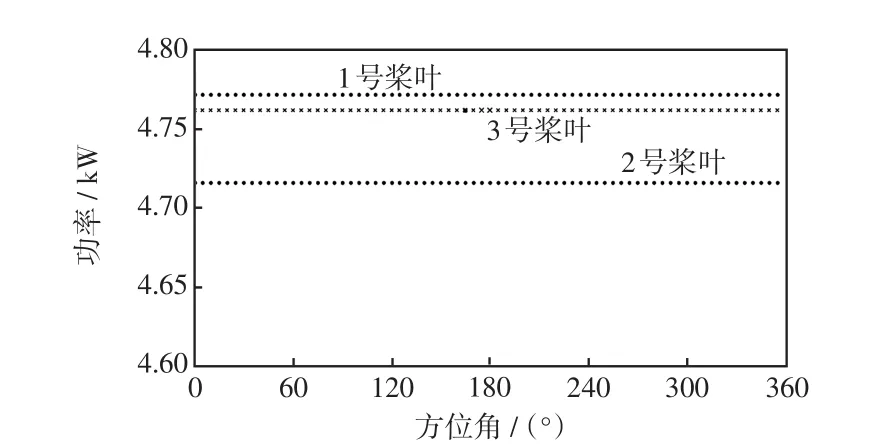
图11 载荷优化模型下的平均输出功率Fig.11 Average power obtained by load optimization model

图12 IPCW和IPCLO仿真下的功率、载荷和桨距角Fig.12 Power，load and pitch angle obtained by IPCW and IPCLO simulation

3.4 IPCLO与IPCW仿真对比分析

仍以1号桨叶为例，分别进行IPCW和IPCLO的仿真，如图12所示。由图12（a）可见，上述2种方法平均功率均在额定值附近，且相差不大。由图12（b）可见，在载荷幅值处，IPCLO较IPCW载荷减小了19%；IPCW载荷变化范围是12～4 kN·m，IPCLO变换范围是10.5～6 kN·m，IPCLO较IPCW受力范围减小了，受力更均匀；由图12（c）可见，IPCLO的桨距角调节相比IPCW次数减少，避免了变桨距机构的频繁动作。图13为IPCLO和IPCW的最大不平衡载荷，由图可知IPCLO的最大不平衡载荷较小且变化范围也较小。本文提出的方法在减小不平衡载荷和载荷幅值的问题上有明显的优越性。另外，在变桨距机构无需频繁调节的同时，输出功率仍维持在额定值附近。

图13 IPCW和IPCLO仿真下的最大不平衡载荷Fig.13 Maximum unbalanced load obtained by IPCW and IPCLO simulation

4 结语

本文针对风剪切效应引起的桨叶不平衡载荷问题，设计了载荷优化模型，在此基础上进行独立变桨距控制。该方法在保证功率的前提下，减小了桨叶间的不平衡载荷，且避免了变桨距机构频繁地调节。相比目前研究较多的权系数独立变桨距控制方法，基于载荷优化模型的独立变桨距控制方法大幅削减了不平衡载荷，且变桨距机构无需频繁动作，对减小风剪切效应影响，延长风轮寿命有重要意义。

[1]郝元钊，李培强，李欣然，等（Hao Yuanzhao，Li Peiqiang，Li Xinran，et al）.风电机组对电力系统暂态稳定性影响分析（Analysing the impact of wind plant on power system transient stability）[J].电力系统及其自动化学报（Proceed⁃ings of the CSU-EPSA），2012，24（2）：41-46.

[2]Carlin P W，Laxson A S，Muljadi E B.The history and state of the art of variable-speed wind turbine technology[J].Wind Energy，2003，6（2）：129-159.

[3]Iniyan S，Herbert G M J，Sreevalsan E，et al.A review of wind energy technologies[J].Renewable&Sustainable En⁃ ergy Reviews，2007，11（6）：1117-1145.

[4]杨秀嫒，梁贵书（Yang Xiuyuan，Liang Guishu）.风力发电的发展及其市场前景（Develoment of wind power genera⁃tion and its market prospect）[J].电网技术（Power System Technology），2003，27（7）：78-79.

[5]邢作霞，陈雷，孙宏利，等（Xing Zuoxia，Chen Lei，Sun Hon⁃gli，et al）.独立变桨距控制策略研究（Strategies study of individual variable pitch control）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（26）：131-138.

[6]耿华，杨耕（Geng Hua，Yang Geng）.变速变桨距风电系统的功率水平控制（Output power level control of variablespeed variable-pitch wind generators）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（25）：130-137.

[7]徐大平，肖运启，秦涛，等（Xu Daping，Xiao Yunqi，Qin Tao，et al）.变桨距型双馈风电机组并网控制及建模仿真（Cutting in control of variable-pitch doubly-fed wind power generation system and its modeling and simulation）[J].电网技术（Power System Technology），2008，32（6）：100-105.

[8]张纯明（Zhang Chunming）.大型风力发电机组独立变桨距控制策略研究（Research on Individual Variable Pitch Con⁃trol Strategies of Large-Scale Wind Turbine）[D].沈阳：沈阳工业大学电气工程学院（Shenyang：College of Electrical Engineering，Shenyang University of Technology），2011.

[9]姚兴佳，马晓岩，郭庆鼎，等（Yao Xingjia，Ma Xiaoyan，Guo Qingding，et al）.基于单神经元权系数的风电机组独立变桨控制（Wind turbine individual pitch control based on sin⁃gle neuron weight coefficient）[J].可再生能源（Renewable Energy Resources），2010，28（3）：19-23.

[10]姚兴佳，刘玥，郭庆鼎（Yao Xingjia，Liu Yue，Guo Qing⁃ding）.基于前馈补偿方位角权系数的分程独立变桨距控制研究（A control method for split range individual pitch based on feed-forward azimuth angle weight number assign⁃ment）[J].太阳能学报（Acta Energiae Solaris Sinica），2012，33（4）：532-539.

[11]马佳（Ma Jia）.大型风力发电机组的独立变桨距控制技术研究（Large-Scale Wind Turbine Individual Pitch Control Technology Research）[D].沈阳：沈阳工业大学电气工程学院（Shenyang：College of Electrical Engineering，Shenyang University of Technology），2012.

[12]Bossanyi E A.Further load reductions with individual pitch control[J].Wind Energy，2005，8（4）：481-485.

[13]Larsen T J，Madsen H A，Thomsen K.Active load reduction using individual pitch，based on local blade flow measure⁃ments[J].Wind Energy，2005，8（1）：67-80.

[14]李晶，王伟胜，宋家骅（Li Jing，Wang Weisheng，Song Jia⁃hua）.变速恒频风力发电机组建模与仿真（Modeling and dynamic simulation of variable speed wind turbine）[J].电网技术（Power System Technology），2003，27（9）：14-17.

[15]贺德馨.风工程与工业空气动力学[M].北京：国防工业出版社，2006.

[16]肖劲松.风力机空气动力学[M].北京：中国电力出版社，2010.

[17]曾庆川，刘浩，LIM Che Wah，等（Zeng Qingchuan，Liu Hao，LIM Che Wah，et al）.基于改进叶素动量理论的水平轴风电机组气动性能计算（Computation of aerodynamic perfor⁃mance for horizontal axis wind turbine based on improved blade element momentum theory）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（23）：99-134.

[18]David Wood.Small Wind Turbines：Analysis Design and Ap⁃plication[M].London：Springer London Ltd，2013.

[19]孔屹刚，顾浩，王杰，等（Kong Yigang，Gu Hao，Wang Jie，et al）.基于风剪切和塔影效应的大型风力机载荷分析与功率控制（Load analysis and power control of large wind tur⁃bine based on wind shear and tower shadow）[J].东南大学学报：自然科学版（Journal of Southeast University：Natural Science Edition），2010，40（S1）：228-233.

[20]周文平，唐胜利，吕红（Zhou Wenping，Tang Shengli，Lü Hong）.风剪切和动态来流对水平轴风力机尾迹和气动性能的影响（Effect of transient wind shear and dynamic in⁃flow on the wake structure and performance of horizontal ax⁃is wind turbine）[J].中国电机工程学报（Proceedings of the CSEE），2012，32（14）：122-127.

[21]杨晓静，徐科，许兵，等（Yang Xiaojing，Xu Ke，Xu Bing，et al）.风电接入电网的评价体系（Evaluation system of wind power grid connection）[J].电力系统及其自动化学报（Pro⁃ceedings of the CSU-EPSA），2015，27（7）：91-95.

Model of Individual Blade Pitch Control of Wind Turbine to Reduce Load

LAN Fei，YANG Meng，WANG Zhehao，JIANG Xing
（School of Electrical Engineering，Guangxi University，Nanning 530004，China）

This paper presents an optimal individual pitch control method for wind turbines operating at high wind speeds to reduce the unbalanced load caused by wind shear while maintaining the rated power，thus prolong the life of wind turbine.According to the principle of aerodynamics，a model of load optimization is established with the minimiza⁃tion of unbalanced load as objective，and restricting the difference between output power and rated power within allow⁃able range as restraint.Using the nonlinear least square method and with the unified individual pitch angles are initial values，the optimal pitch angles corresponding to three blades are calculated，and these angles are further used as refer⁃ence values to realize individual pitch control，respectively.Simulation results indicate that compared with the tradition⁃al pitch control method，the proposed model can reduce the unbalanced load significantly and avoid the loss of power and the frequent pitching.

optimal individual pitch control；load optimization；wind shear effect；collective pitch control；unbal⁃anced load

TK8

A

1003-8930（2016）11-0037-07

10.3969/j.issn.1003-8930.2016.11.007

2015-01-12；

2016-01-04

国家自然科学基金项目（51277034）

兰 飞（1974—），男，硕士，高级工程师，硕士生导师，研究方向为电力系统安全运行与控制、大规模可再生能源发电的接入及其运行与控制技术等。Email：lanfei88@163.com

杨 萌（1989—），女，硕士研究生，研究方向为电力系统安全运行与控制。Email：ymm@mail.gxu.cn

王哲豪（1990—），男，硕士研究生，研究方向为电力系统安全运行与控制。Email：ZhehaoWang05@126.com