Electromechanical dynamics analysis and simulation on rollforming equipment with both sides variable cross-section①

Yan Jun (闫 军), Li Qiang, Zhou Zhixia*

(*College of Mechanical Engineering, Inner Mongolia University of Technology, Hohhot 010051, P.R.China)(**College of Mechanical and Material Engineering, North China University of Technology, Beijing 100000, P.R.China)(*** College of Electrical Power, Inner Mongolia University of Technology, Hohhot 010051, P.R.China)



Electromechanical dynamics analysis and simulation on rollforming equipment with both sides variable cross-section①

Yan Jun (闫 军)②*, Li Qiang**, Zhou Zhixia***

(*College of Mechanical Engineering, Inner Mongolia University of Technology, Hohhot 010051, P.R.China)(**College of Mechanical and Material Engineering, North China University of Technology, Beijing 100000, P.R.China)(***College of Electrical Power, Inner Mongolia University of Technology, Hohhot 010051, P.R.China)

Electromechanical dynamics analysis and simulation on a rollforming equipment with both sides variable cross-section are discussed in this study. The system includes mechanical parts and electromagnetism parts, and it is a strongly coupled electromechanical system. Based on a virtual work principle and given power，generalized forces of this system are obtained. By using Lagrange-Maxwell equations, a model of electromechanical dynamics is established. Differential equations of two-phase winding on d-q axis are obtained by Park transformation, which comes from three-phase winding equations on the A-B-C axis. This system is solved with the 4th order Runge-Kutta’s method, and discrete solutions of all variables are obtained. Finally, by using Matlab language, the system is simulated. The results show that the proposed method works very well.

electromechanical dynamics, electromechanical coupling system, virtual work principle, Runge-kutta’s method

0 Introduction

The electromechanical dynamics model of a system is the foundation of theoretical research to the system. By establishing an electromechanical dynamics model validly, motion characteristics of each part in the system can be got, and the whole system can be controlled accurately. The electromechanical dynamics model is very complex, because it covers theoretical basis of many fields, including mechanics, electricity and their interdisciplinary subjects[1-3]. It is from the viewpoint of energy to represent the relation among movement parameters of each part, which can simplify this problem. It is considered in electromechanical dynamics model that mechanical part and electromagnetism part are unified. In motor model, the magnetic field and electromagnetic energy are united with the motion and kinetic energy in mechanical part.

1 Composition of the system and motion analysis

Composition of the rollforming system equipment is shown in Fig.1. Four servomotors at the bottom are the source of power to drive the whole bed frame translational motion or rotational motion. By screw pair, the rotational motion of bottom two servomotors is turned into translational motion, cover nut and gear rack linking together. If the speed of bottom No.1 servomotor is equal to No.1 servomotor’s, the gear meshes with the two gear racks at the same time, and they have the same speed. At this time, the gear, bed frame on it and its support will move along their track.

Fig.1 Bottom schematic diagram of mechanism

When speeds of two motors are not equal, the gear meshes with two gear racks at the same time, and their speeds are not equal. At this time, the gear and its support will move along their track, but the gear and bed frame on it will turn and move. Side schematic diagram of mechanism is shown in Fig.2.

Fig.2 Side schematic diagram of mechanism

The mechanism endures load F1, load F2, torque T1 and torque T2, where F1=-F2, T1=-T2. Load F1 varies with time, as shown in Fig.3. Torque T1 also varies with time, as shown in Fig.4.

Fig.3 Diagram of load F1 varied vs. time

Fig.4 Diagram of torque T1 varied vs. time

2 System parameter and energy analysis

Parameters of the system is as follows, as shown in Table 1.

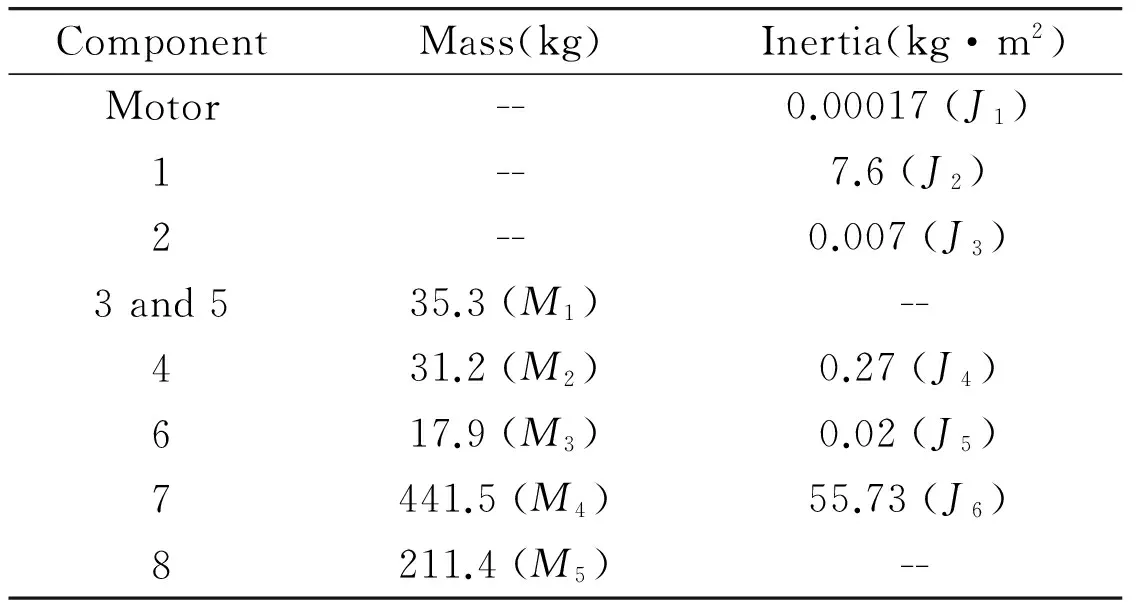
Table 1 Parameters of component

Electromechanical dynamics model of the system is discussed from the viewpoint of energy in this paper. Inertia of rotor is J1. Rated torque of motor is T0. The turning angle of four servomotor at bottom are φ1,φ2,φ3,φ4. Inertia of reducer is J2, and reduction rate is 20. Inertia of screw is J3and pitch is 8mm, u=p/(2π). Inertia of bed frame, gear and support shaft is J4,J5,J6, respectively. J=J4+J5+J6. Radius of gear is R. Total rotational kinetic energy TT1is as follows:

(1)

Mass of cover nut and gear crack is M1. Mass of bed frame is M4. Mass of gear is M2. Mass of support shaft is M3. Mass of bottom support is M5. Define: M=M2+M3+M4+M5, Translational kinetic energy of this system TT2is as follows[4,5]:

(2)

Total kinetic energy T is as follows:

T=TT1+TT2

(3)

sortting out：

(4)

Define:

Substituting into Eq.(4) as follows：

(5)

The magnetic energy of this system Wmis, as follows:

(6)

Labc1, iabc1and ψabc1are inductance, current and flux linkage of stator on motor 1.

3 Differential equations of the whole system

Lagrange-Maxwell equations:[6-8].

(7)

where Lagrange function L is

L=T+Wm

(8)

The dissipation function is F, as follows:

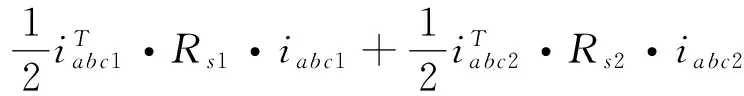
(9)

where B, Rsare viscous damping and resistance of motor. According to Lagrange-Maxwell equations, derivative calculation to Lagrange function L and dissipation function F are carried out as follows:

Substituting into Eq.(7) as

(10)

Motor 1,2,3,4 are taken into account, the Lagrange-Maxwell equation is

(11)

Based on the work theory of mechanics of materials, the generalized forces Q1, Q2, Q3, Q4are calculated as follows:

(12)

By Park transformation, Larange-Maxwell equations under d and q axis are obtained：

(13)

where P is number of pole-pairs of stator. ud1, uq1are voltage of d and q axes. They are controlled and can be obtained by program, which is shown in Fig.5. Currents of d and q axes are id1and iq1. Ld1, Lq1are inertia of rotor of d and q axes.

4 System Parameters and controlling principle:

Parameters of servomotor MKE047 is as follows, as shown in Table 2.

Table 2 Parameters of the servo motor

Control model of id=0 is used in this study, where electromagnetic force is directly proportional to iq.[9-11]

The flow chart of controlling and solving program is shown in Fig.5.

Fig.5 Chart of controlling program and solving

5 System simulation[12,13]:

The rollforming system carries loads shown in Fig.3 and Fig.4. It shows that the effects of loadF1 and torqueT1 to No.1 and No.2 motors are different in Fig.1, which makes their motion parameters different. Solutions of Eq.(13) are obtained by using the 4th order Runge- Kutta method in Matlab language. The simulation result of electromagnetic torque is shown in Fig.6. The electromagnetic torque of No.1 motor spindle is shown with solid line, while No.2 is shown with dash line. They are very different, when external loads are added to the system, electromagnetic force is varied. When the processing pieces go through the equipment, the electromagnetic force tends to be constant.

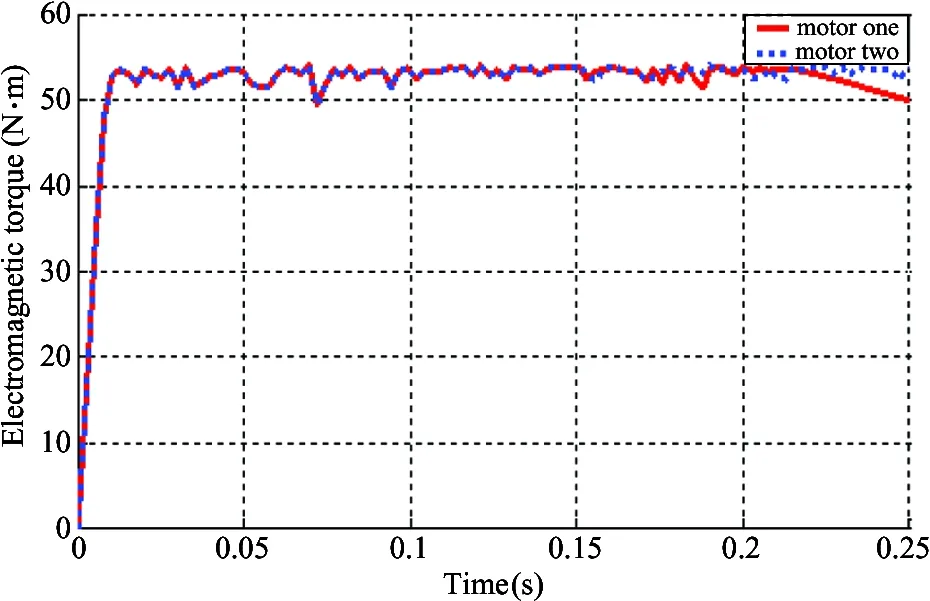
Fig.6 Figure of electromagnetic torque vs. time

Changes of angle of the motor spindles versus time are shown in Fig.7. The angle of No.1 motor spindle is shown with the solid line, while No.2 is shown with the dash line. They are very different.

Fig.7 Figure of motor rotate angle vs. time

Changes of angle velocity in motor spindle versus time are shown in Fig.8. It shows that the angle velocity of motor spindle changes obviously as the loads change, which is accordant with practice situation. The angle velocity of No.1 motor spindle is shown with

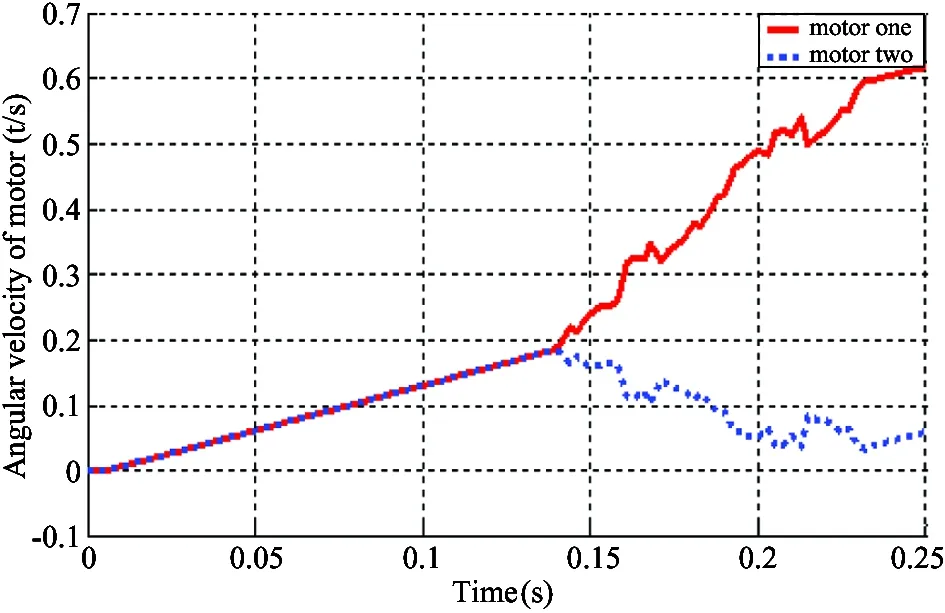
Fig.8 Figure of angular velocity vs. time

solid line, while No.2 is shown with dash line. They are different greatly. Comparing the solid line in Fig.7 with that in Fig.8, the relationship between angle displace and angle velocity is attained.

Changes of angle acceleration of motor spindle versus time are shown in Fig.9. The angle acceleration of No.1 motor spindle is shown with solid line, while No.2 is shown with dash line. They are different obviously. Comparing Fig.6 and Fig.7 with Fig.8, the relationship of angle displace, angle velocity and angle acceleration is attained.

Fig.9 Figure of motor acceleration vs. time

The current of axis d and q is shown in Fig.10, where the current of axis d is fluctuant around zero, the current of axis q is proportional to electromagnetic torque in accordance with the adopted control model of id=0.

Fig.10 Chart of d-q axis current vs. time

The current of axis A-B-C is shown in Fig.11. The three phase current is a sine curve broadly, consistent with the requirements of the motor.

Fig.11 Chart of A-B-C axis current vs. time

6 Conclusion

(1)The composition and motor process of each member in this system are discussed in this paper.

(2)A dynamic model of mechanism is structured in this system, where the generalized force is obtained on virtual work principle.

(3)Electromechanical dynamics model is established by Lagrange-Maxwell equations.

(4)By four Runge-Kutta’s method in matlab, solution of differential equations are obtained. From simulation result, the model and its solving process are correct and reasonable.

[ 1] Yamapi R, Kakmeni F M M, Orou J B C. Nonlinear dynamics and synchronization of coupled electromechanical systems with multiple functions.CommunicationsinNonlinearScienceandNumericalSimulation, 2007, 12(4)：543-567

[ 2] Lipiński K. Multibody and electromechanical modelling in dynamic balancing of mechanisms for mechanical and electromechanical systems.DiffusionandDefectDataPartB:SolidStatePhenomena, 2009，147：339-344

[ 3] Wu J X, Li Q, Zhao W G, et al. Dynamical modeling and momputation on mlectromechanical coupling system of grain reshaping machine tool for solid propellant rocket motor.ChineseJournalofMechanicalEngineering, 2008, 44(3):110-116 (In Chinese)

[ 4] Xu F, Guo Y, Yu W, et al. Simulation and analysis on electromechanical dynamics of optical-electric theodolite.ActaPhotonicaSinica, 2008 ,37 (10) :2076-2079 (In Chinese)

[ 5] Chen S J， Guo Z S，Jiang S H. Research of permanent magnetism synchronous motor servo control system by matlab simulation.JournalofAnqingTeachersCollege(NaturalScienceEdition), 2011, 17(4):60-62 (In Chinese)

[ 6] Wu J X. Dynamics Analysis and Optimization on Electromechanical Coupling System of Solid Rocket Motor Reshaping Machine Tool:[Ph. D dissertation]. Hohhot: College of Mechanical Engineering, Inner Mongolia University of Technology, 2007. 10-30 (In Chinese)

[ 7] Jiang F R. Sevro Control System Study of Permanent Magnet Synchronous Motor:[Ph. D dissertation]. Hangzhou: College of Electrical Engineering, Zhejiang University, 2006. 15-30 (In Chinese)

[ 8] Liang Z H, Han Y, Fa N G. Grey PID control of permanent magnet synchronous motor servo control system.JournalofShenyangUniversityofTechnology, 2008, 30(6): 619-622 (In Chinese)

[ 9] Zhang R, Bai L P. Research on permanent magnet AC servo motor control system.ElectricalEngineering, 2011, 3: 6-9 (In Chinese)

[10] Darula, Radoslav; Sorokin, Sergey. On non-linear dynamics of a coupled electro-mechanical system.NonlinearDynamics, 2012, 70(2): 979-998

[11] Sun X Y, Xie Z J, Jian K L, et al. Dynamics analysis and simulation of 6-PSS flexible parallel robot.TransactionoftheChineseSocietyforAgriculturalMachinery, 2012, 43(7)：194-199 (In Chinese)

[12] Yan J, Li Q, Wu J X. Electromechanical dynamics analysis and simulation on roll-forming equipment based on linear motor.InternationalJournalofModellingandSimulation, 2014, 34(3): 126-133

[13] Handani D W. System dynamics simulation for constructing maintenance management of ship machinery. In: Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 2011. 1549-1553

Yan Jun, born in 1974. He received his Ph.D degrees in College of Mechanical Engineering, Inner Mongolia University of Technology in 2015. His research interests include electromechanical dynamics and mechanical design.

10.3772/j.issn.1006-6748.2016.01.011

① Supported by the National Science and Technology Support Program (No. 2011BAG03B03) and Inner Mongolia University of Technology Science and Research Projects of China(No. X201338).

② To whom correspondence should be addressed. E-mail: yan_jun11@163.comReceived on July 10， 2015