静动荷载作用下简支预应力混凝土曲线箱梁剪力滞效应分析
卢海林,张山,万崇勇,王琛,蔡恒
武汉工程大学资源与土木工程学院,湖北 武汉 430074
静动荷载作用下简支预应力混凝土曲线箱梁剪力滞效应分析
卢海林,张山,万崇勇,王琛,蔡恒
武汉工程大学资源与土木工程学院,湖北武汉430074
选择集中荷载与均布荷载作为静荷载,地震作用与行车荷载作为动荷载,建立曲线箱梁三维空间实体有限元模型.通过静力分析和动荷载作用下时程反应分析,研究跨中截面顶板剪力滞系数变化规律.结果表明:在静动两种荷载作用下,剪力滞系数的最大值都出现在顶板与腹板交界处;在两种静荷载的作用下,剪力滞效应仅在顶板与腹板交界处明显,其它区域微弱,并且剪力滞系数不随荷载值的变化而变化;在天津波作用下,顶板各节点剪力滞系数在0.978~1.045之间,剪力滞效应不明显;在EL Centro波作用下,剪力滞效应明显,各节点剪力滞系数在0.065~4.12之间变化;在行车荷载作用下,剪力滞效应比较明显,剪力滞系数在0.42~2.08之间变化,外侧剪力滞系数峰值明显大于内侧,且剪力滞系数随着车速的增加而增加.
剪力滞效应;静动荷载;曲线箱梁;预应力混凝土
1 引言
在现代桥梁建设中,曲线桥梁的使用日趋频繁.为实现城市立交工程中各方向交通畅通,曲线桥梁做出了重要的贡献,在山区高速公路的选线设计中,在必要的地段采用曲线桥梁,可以节省预算与减小展线的长度.而曲线箱梁因其独特的力学特性和构造特点成为了运用最广泛的曲线桥梁.曲线箱梁具有良好的稳定性,使其便于施工,同时曲线箱梁还具有自重轻、截面抗弯、抗扭刚度大等特点.除此之外,曲线箱梁能适应现代施工方法的要求,便于布置管线等公共设施.
近些年来,各国学者对于曲线箱梁的力学性能的分析方法做了很多研究,主要的分析方法有:经典解析法[1]、能量变分法[2]、比拟杆法[3]、有限元的数值解法[4]、模型试验法[5].朱明坤[6]等通过基于ANSYS的有限元分析,发现了预应力混凝土曲线箱梁在均布荷载作用下,顶板与底板上的剪力滞系数会由腹板和顶板与腹板交界处向两边逐渐减小,且顶板上的剪力滞系数要大于腹板下的剪力滞系数.本文中静荷载选择集中荷载与均布荷载两种,动荷载选择地震荷载与行车荷载两种.通过对简支预应力混凝土曲线箱梁进行有限元分析,阐述了在静动荷载作用下跨中截面顶板的剪力滞效应.与之前学者的研究内容相比,增加了分别在两种大小不同的集中荷载与均布荷载作用下跨中顶板剪力滞系数分布的对比,同时还增加了在动荷载作用下对预应力混凝土曲线箱梁的剪力滞效应的分析.
2 实验部分
2.1剪力滞系数
箱梁的腹板与顶板交界处在受到竖向对称载荷作用的时候,如果只根据平截面假定基本梁理论计算,将不考虑在箱梁纵向的剪切变形.在这种情况下,沿着箱梁顶板上、下翼缘板的正应力分布是均匀的.然而,横向应力会从腹板传递到翼板上,进而导致剪力在翼板中的分布不均匀:在翼板与腹板交界处达到最大,离腹板越远剪力值会越小.由此可以得出,曲线箱梁顶板上产生的剪力滞效应分布是不均匀的.出现在顶板上的剪力滞效应分布不均匀的现象被称为“剪力滞效应”[7-8].当顶板与腹板交界处的剪力滞系数大于其它区域的剪力滞系数时,称这种现象为“正剪力滞效应”,所以当顶板与腹板交界处的剪力滞系数小于其它区域的剪力滞系数时,这种现象称为“负剪力滞效应”[9],如图1所示.

图1 (a)正剪力和(b)负剪力滞现象Fig.1Lag effect of(a)positive shear and(b)negative shear
为了定量研究剪力滞效应的大小,按公式(1)计算:

式(1)中,σ为横截面上计算得出实际应力值,σ¯为按照初等梁理论计算得到的应力值.
2.2有限元模型的建立
2.2.1结构形式本文中的研究模型选用的是一个实际工程中的预应力混凝土曲线箱梁桥.本桥为互通式立体交叉的一个匝道桥,桥梁为单幅桥,桥长34 m,桥宽9.0 m,曲率半径为135 m.上部主梁的预应力混凝土采用C50,轴心抗压强度标准值fck=32.4 MPa,轴心抗拉强度标准值ftk=2.65 MPa,弹性模量Ec=3.45×104MPa.预应力钢绞线采用d= 15.2 mm的七股Ⅱ级松弛(低松弛)钢绞线,布置位置如图2所示,其抗拉强度标准值fpk=1 860 MPa,张拉控制应力值为0.75fpk=1 395 MPa,钢绞线弹性模量Ep=1.95×105MPa.截面尺寸如图3所示.

图2 预应力钢束布置位置(单位:cm)Fig.2Arrangement position of prestressed steel beam(unit:cm)

图3 预应力混凝土曲线箱梁尺寸(单位:cm)Fig.3Dimension of prestressed concrete curved box girder(unit:cm)
2.2.2计算模型本文采用《混凝土结构设计规范》GB50010—2002[10]混凝土的本构模型:
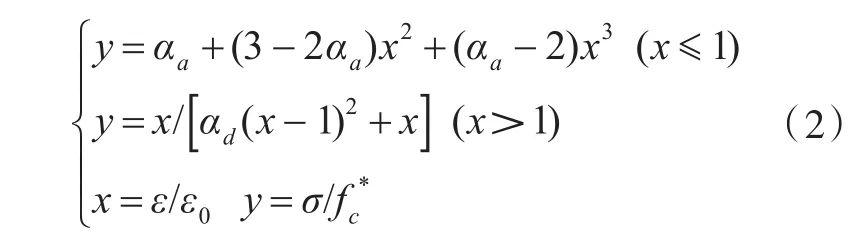
式(2)中:αa、αd分别代表混凝土单轴受压曲线上升段与下降段的参数值;fc*代表混凝土的单轴抗压强度(fck、fc或fcm);ε0代表与fc*相应的混凝土峰值应变值,σ为混凝土单轴受压曲线的应力值.
按照现有的预应力混凝土结构设计原理,本文研究的曲线箱梁采取不配普通钢筋[11].其中,预应力钢束只采用平弯,不考虑竖弯.混凝土部分采用Soild65进行模拟,预应力钢束部分采用Link8进行模拟,约束条件采用文献[12]中的简支约束条件.网格划分采用按边布种,ANSYS中预应力混凝土曲线箱梁的有限元模型如图4所示.

图4 预应力混凝土曲线箱梁有限元模型Fig.4Finite element model of prestressed concrete curved box girder
3 结果与讨论
3.1集中荷载
沿纵向采用大小分别为0.6 kN、1.2 kN的2种集中荷载对称的施加于跨中截面箱梁顶板与腹板交界处.计算后得到跨中截面顶板各节点的剪力滞系数,结果如图5所示.
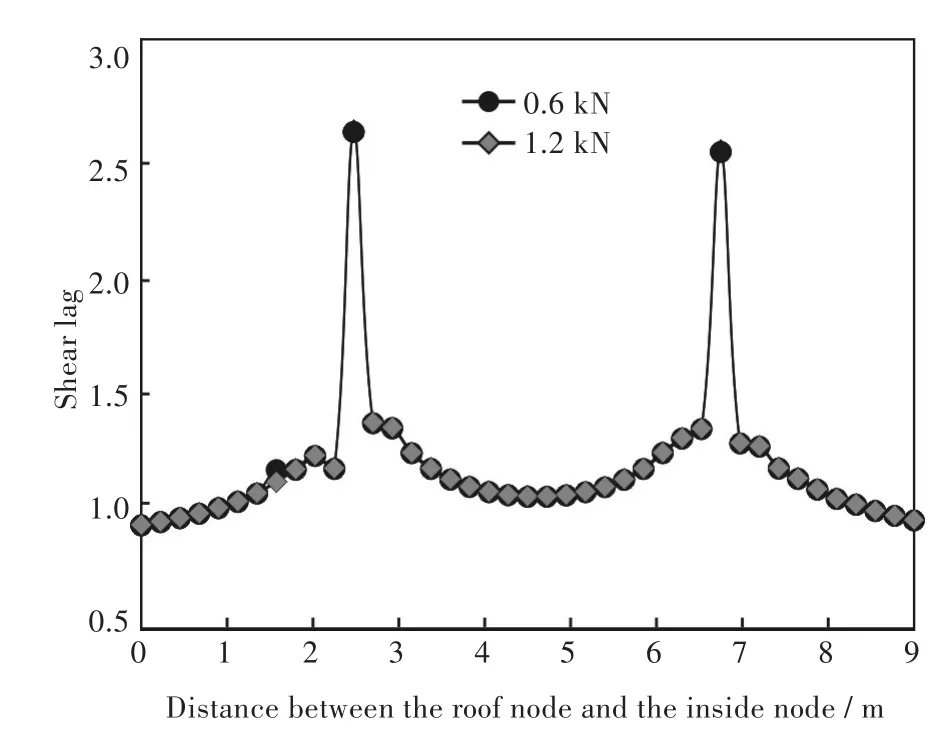
图5 集中荷载下跨中截面顶板剪力滞系数分布Fig.5Shear lag coefficients distribution of cross-section roof under concentrated load
由图5可知,在集中荷载作用下预应力混凝土曲线箱梁跨中截面顶板的剪力滞效应明显.在顶板与腹板交界处剪力滞系数达到最大,峰值接近2.6.随着荷载成倍的增加,剪力滞系数基本上不发生变化.
3.2均布荷载
沿纵向采用大小分别为0.5 MPa、1.0 MPa的2种均布荷载施加于箱梁顶板上.计算得到跨中截面顶板各节点的剪力滞系数,如图6所示.

图6 均布荷载下跨中截面顶板剪力滞系数分布Fig.6Shear lag coefficients distribution of cross-section roof under uniform load
从图6可以看到,在均布荷载作用下剪力滞效应分布趋势与集中荷载作用下的类似.剪力滞系数均在顶板与腹板交界处达到最大,波动于0.98~1.05之间.随着荷载成倍的增加,剪力滞系数仅在跨中截面中心附近区域出现微小波动.但总体来说,跨中截面顶板的剪力滞效应在均布荷载作用下表现并不明显.
3.3地震荷载
3.3.1天津波天津波,时间间隔为0.1 s,持续时间为5 s,分析中选用天津波水平方向加速度时程曲线,如图7所示.本文对天津波原始的记录数据进行处理,将实际地震记录的分支折算成计算所需的基本烈度[13],即将天津波的记录数据值乘以0.420 5后得到修正后的加速度值.

图7 天津波加速度曲线Fig.7Acceleration curve of Tianjin wave
在剪力滞效应的影响下,曲线箱梁顶板与腹板交界处区域的应力值要大于其它区域的应力值,所以本研究主要分析跨中截面顶板与内侧腹板交界处节点的地震响应,计算可得该节点的剪力滞系数,如图8所示.

图8 顶板与内侧腹板交界处节点剪力滞系数随时间变化Fig.8Shear lag coefficients of lateral junction node of roof and inside web changing with time
由图9中可知,剪力滞系数随着时间的变化不断的发生变化,但是节点的剪力滞系数在0.978~1.145之间变化.即在地震这种不停变化的动荷载作用下,曲线箱梁顶板和内侧腹板交界处节点的剪力滞系数均在一个固定值上下浮动.取横截面上其它节点分析,也存在同样的现象.因此,在地震作用下,跨中截面顶板上的剪力滞效应趋于稳定.由此可得,在研究某个节点的剪力滞系数时,选取它的平均值作为这一固定值,即为该节点最终的剪力滞系数[14].
输入修正后的天津波,计算可得跨中截面顶板各节点的剪力滞系数,结果如图9所示.

图9 地震荷载下t=3.2 s时跨中截面顶板剪力滞系数分布Fig.9Shear lag coefficients distribution of cross-section roof under seismic load at 3.2 s
由图9可知,在地震作用下跨中截面顶板的剪力滞系数分布大致对称,在顶板与腹板交界处剪力滞系数达到最大,波动于0.987~1.045之间,剪力滞系数趋于稳定,剪力滞效应不明显.
3.3.2EL波EL Centro波,时间间隔为0.02 s,持续时间为30 s.分析中选用EL Centro波水平方向加速度时程曲线.选取0 s~6 s的加速度输入到ANSYS中计算,如图10所示.
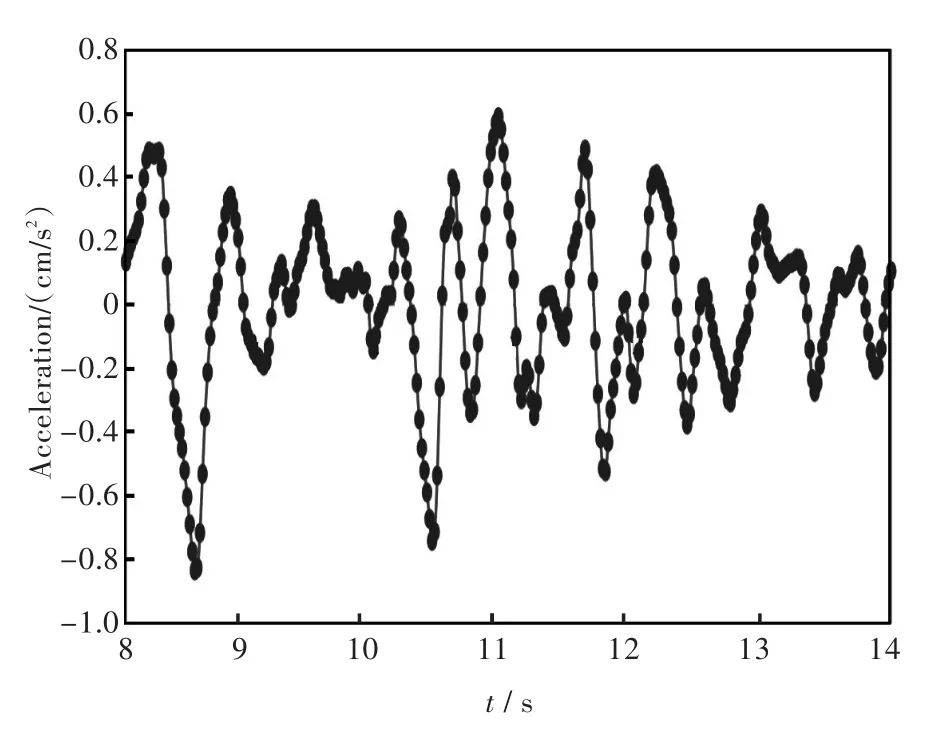
图10 EL波加速度曲线Fig.10Acceleration curve of EL wave
数据处理后得到跨中截面顶板上各节点的剪力滞系数和顶板与内侧腹板交界处节点的剪力滞系数,如图11、图12所示.
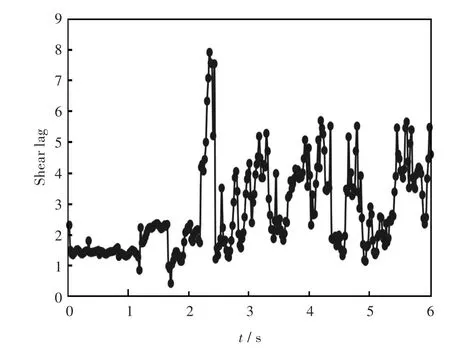
图11 对顶板与内侧腹板交界处节点剪力滞系数随时间变化曲线Fig.11Shear lag coefficients of junction of roof and inside web changing with time

图12 地震荷载下t=2.4 s时跨中截面顶板剪力滞系数分布Fig.12Shear lag coefficients distribution of cross-section roof under seismic load at 2.4 s
由图11可知,曲线箱梁顶板和内侧交界处节点的剪力滞系数随着时间的变化也在不断的发生着变化,剪力滞系数在0.44~7.29之间上下浮动.在EL Centro波这种强震作用下,节点的剪力滞系数随时间的变化变的不规律,但是大部分节点的剪力滞系数集中在1.5~5之间.随着地震动力变的更显著,节点剪力滞系数的变化也变得杂乱无章.
由图12可知,顶板上各节点的剪力滞系数在不同时刻不相同,剪力滞效应明显,但分布极不均匀;在顶板与腹板交界处剪力滞系数达到最大,其余各节点的剪力滞系数都处于0.065~4.12之间.随着地震动力变的更显著,顶板各节点剪力滞系数变化较大.
3.4行车荷载
本文采用荷载大小为f=3.75 kN,速度分别为v=10 m/s、v=15 m/s的移动荷载沿着曲线箱梁的行车道施加,行车道位置如图13所示,图13(a)为内侧行车道,图13(b)为外侧行车道,图中F1=F2=F3= F4=F.通过计算,可以得到跨中截面顶板上各节点的剪力滞系数,其曲线如图14所示.

图13 行车道位置Fig.13Lane position

图14 行车荷载下跨中截面顶板剪力滞系数分布Fig.14Shear lag coefficients distribution of cross-section roof under vehicle load
由图14中可以看出,在行车荷载的作用下,顶板各节点剪力滞系数在0.42~2.08之间变化,节点的剪力滞系数在顶板与腹板交界处达到最大,且外侧剪力滞系数峰值大于内侧,剪力滞效应比较明显.在荷载大小相同的条件下,随着车速的增加,剪力滞系数增大.
4 结语
1)针对跨度为34 m、曲率半径为135 m的简支预应力混凝土曲线箱梁的有限元分析表明:在静动荷载作用下,在顶板和腹板交界处剪力滞系数达到最大,并沿着顶板和腹板交界处向两边的区域逐渐变小.
2)在静荷载作用下,跨中截面顶板上的剪力滞效应明显.集中荷载作用下跨中截面顶板上产生的剪力滞大于在均布荷载作用下顶板上产生的剪力滞.在集中荷载与均布荷载作用下,随着荷载的倍增,剪力滞效应几乎不发生变化,可以忽略不计.
3)在天津波作用下,跨中截面顶板的剪力滞效应不明显;在EL Centro波强震作用下,各节点的剪力滞系数在不同时刻的剪力滞系数不同,分布极不均匀,剪力滞效应明显.与静荷载的作用相比,曲线箱梁在地震作用下表现出了更强烈的动力响应.地震动力越显著,剪力滞效应越明显.
4)行车荷载作用下,顶板上产生的剪力滞效应比较明显,且顶板外侧区域中的剪力滞系数明显大于内侧区域中的剪力滞系数,顶板上各节点的剪力滞系数基本上大于1.在保持荷载大小不变的情况下,随着车速的增加,剪力滞系数增大.
致谢
武汉工程大学交通研究中心为本研究提供软件支持,在此表示感谢!
[1]李法雄,聂建国.钢-混凝土组合梁剪力滞效应弹性解析解[J].工程力学,2011,28(9):1-8.
LI F X,NIE J G.Elastic analytical solutions of shear lageffectofsteel-concretecompositebeam[J]. Engineering mechanics,2011,28(9):1-8.
[2]张元海,李乔.考虑剪滞变形及约束扭转二次剪切变形影响时薄壁曲线箱梁的挠曲扭转分析[J].土木工程学报,2009,42(3):93-98.
ZHANG Y H,LI Q.Flexural-torsional analysis of thin-walled curved box girders with shear lag and secondary shear deformation in restraint torsion[J]. China civil engineering journal,2009,42(3):93-98.
[3]周茂定,刘世忠,杨子江.波形钢腹板组合箱梁剪力滞效应的比拟杆法求解[J].兰州交通大学学报,2012,31(4):41-44. ZHOU M D,LIU S Z,YANG Z J.Bar simulation method onshearlageffectofcompositeboxgirderwith corrugated steel web[J].Journal of Lanzhou jiaotong university,2012,31(4):41-44.
[4]卢海林,张伟,颜昌雄.移动荷载速度对悬臂曲线箱梁剪力滞效应的影响[J].武汉工程大学学报,2014,36(3):18-21. LU H L,ZHANG W,YAN C X.Moving load speed on shear lag effect of cantilever curved box girde[J]. Journal of Wuhan instute technology,2014,36(3):18-21.
[5]吴文清,叶见曙,万水,等.波形钢腹板结合箱梁在对称加载作用下剪力滞效应的试验研究[J].中国公路学报,2003,16(2):48-51. WU W Q,YE J S,WAN S,et al.Experiment study of shear lag effect of composite box girder with corrugated steel web under the symmetrical load[J].China journal of highway and transport,2003,16(2):48-51.
[6]朱明坤.预应力混凝土箱梁的剪力滞效应研究[D].长沙:湖南大学,2013.
[7]FOUTCH D A,CHANG P C.A shear lag anomaly[J]. Journal of the structural division,1982,108(7):1653-1658.
[8]SUNG C L,CHAI H Y,DONG Y.Analysis of shear lag anomaly in box girders[J].Journal of the structural division,2002,128(11):1379-1386.
[9]SHUSHKEWICH K W.Negative shear lag explained[J].Journal of the structural division,1991,117(11):3543-3546.
[10]中国建筑科学研究院.混凝土结构设计规范:GB50010—2002[S].北京:中国建筑工业出版社,2002:93.
[11]季文玉,周超民.预应力RPC箱梁剪力滞效应分析[J].中国铁道科学,2007,28(1):19-22. JI W Y,ZHOU C M.Shear Lag analysis of prestressed RPC box girder[J].China railway science,2007,28(1):19-22.
[12]李洪.曲线连续箱梁桥剪力滞效应分析及实用计算[D].北京:北京交通大学,2010.
[13]卢海林,朱松波,周小龙,等.不同荷载作用下直线箱梁剪力滞效应分析[J].武汉工程大学学报,2014,36(12):39-43. LU H L,ZHU S B,ZHOU X L,et al.Shear lag effect of straight box girder under different loads[J].Journal of Wuhan instute technology,2014,36(12):39-43.
[14]LU H L,CHEN L P,ZHU S B,et al.Analysis of effect factorsabout shear lag in cur-vedbox girder under seismic loads[J].Advanced materials research,2014,926-930:505-510.
本文编辑:陈小平
Shear Lag Effect of Curved Box Girder of Simply-Supported Prestressed Concrete Under Static and Dynamic Load
LU Hailin,ZHANG Shan,WAN Chongyong,WANG Chen,CAI Heng
School of Resource and Civil Engineering,Wuhan Institution of Technology,Wuhan 430074,China
The solid finite element model of the curved box girder was built using concentrated and uniform load as the static load,and seismic and vehicle load as the dynamic load.The distribution of shear lag coefficients on the top plate at mid-span was explored by static and dynamic time-history analysis.The analytical results show that the shear lag coefficients reach their peak values at the junction of the top plate and the web of curved box girder under the static and dynamic load.The shear lag effect is strong at the junction of the top plate and the web under the static load,but it is weak in the rest areas;while,the shear lag coefficients do not change with the reduction or amplification of the valves of the static load.The shear lag effect is weak with coefficients in 0.978-1.045 under the seismic load of the Tianjin wave,but it is strong with coefficients in 0.065-4.12 under the seismic load of the EL Centre wave.The shear lag effect is strong with coefficients in 0.42-2.08 under the vehicle load,and it is stronger in the areas of exterior web than that in the inner web,moreover,the shear lag coefficients increase with the increase of the vehicle speed.
shear lag effect;static and dynamic load;curved box girder;prestressed concrete
U448.42
A
10.3969/j.issn.1674⁃2869.2016.05.011
1674-2869(2016)05-0465-06
2016-03-31
国家自然科学基金(51378404)
卢海林,博士,教授.E-mail:1257587787@qq.com

