基于二分图的宝鸡公交线路-站点网络建模及分析

王欢, 胡静波

(宝鸡文理学院 a.计算机学院；b. 电子电气工程学院，陕西 宝鸡 721016)



基于二分图的宝鸡公交线路-站点网络建模及分析

王欢a, 胡静波b

(宝鸡文理学院 a.计算机学院；b. 电子电气工程学院，陕西 宝鸡 721016)

复杂网络理论已成为研究交通系统的有效工具。以陕西省宝鸡市的43个公交线路及344个公交站点数据为基础，基于二分图理论，构建了站点-线路公交网络模型，并对该网络的统计性质进行了分析。研究结果表明，网络中的线路节点度分布呈现泊松分布，大部分线路度值集中在平均值附近；而站点节点度分布呈现幂律分布，其中的少数节点高度连接，为网络中的关键枢纽节点。这些高度连接的线路和站点可被筛选为宝鸡市交通网络研究中的重点规划对象。

复杂网络；二分图；公交网络；度分布；枢纽节点

0 引 言

自然界和人类社会中存在的大量复杂系统都可以被抽象为网络，通过研究个体之间的相互关系及探索系统整体呈现出的性质，找出其中的规律性及共性[1-2]。复杂网络理论是研究这种复杂系统的有力工具，现已被大量应用在生物、经济、社会、交通和管理等各个领域[3-5]。

交通系统是一种最为典型的复杂系统，而公交系统则是城市的交通命脉，研究公交系统网络对于城市的交通发展和交通优化具有重大的意义[6-7]。公交系统包含有公交线路和公交站点两个方面，已有的国内公交网络的研究基本都是针对单独的公交线路或者公交站点，而将公交线路与公交站点结合起来研究城市公交系统则更具有实际的指导意义。

本文以陕西省宝鸡市43条公交线路和344个公交站点为基础，构建了公交系统线路-站点二分网络模型，计算并分析了网络中不同类节点的度值及其分布特征，并结合城市公交系统的实际情况，研究了宝鸡市公交网络中线路与站点的关联信息，为公交系统的优化提供理论依据。

1 宝鸡公交二分网络的构建

在复杂网络的研究中，如果希望得到两种不同的事物之间存在的某种关联性，可通过构建两种不同类型节点的网络以便研究节点之间的从属关系，这种网络就称为二分图(bipartite graph)[8]。

定义一个二分图G=(V,E)，其中V={V1,V2}代表网络中的节点的集合，节点集合V被划分为两个不相交的子集V1和V2，分别代表两种不同类型的节点；E={V1i,V2j}是连接两个不同子集中的节点之间的所有边的集合，而同一子集中的节点之间没有连线，其中i=1,2,…,N1，j=1,2,…,N2，N1和N2分别为两个不同子集中的节点个数。

宝鸡市公交公司目前一共拥有43条线路，共经过344个不同的站点，考虑公交线路和公交站点两个方面之间的联系，我们构建线路-站点二分网络。网络中共包含387个节点，被分为两类：N1=43条线路作为一类节点，记为V1；N2=344个站点作为另一类节点，记为V2。当V1中的线路i经过了V2中的站点j，则节点i与j之间存在一条边；反之，则两个节点之间不存在连边。表1列出了一些随机选择的线路节点与站点节点之间的对应关系。其中，如果两个节点间有对应关系，则用1表示；反之，则用0表示。

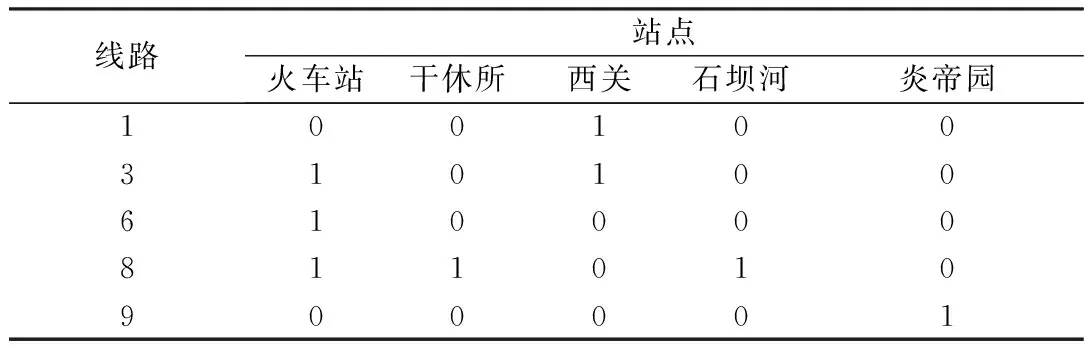
表1 线路节点与站点节点之间的关系示意表

图1 宝鸡公交线路-站点二分图

将表1所列举的这种网络节点之间的对应关系用图的形式表示出来，即为线路-站点二分图，如图1所示。从图中可以直观地显示出线路节点与站点节点之间的对应关系，而同种类的节点之间并没有连边存在。

2 宝鸡公交二分网络的统计性质

复杂网络中，一个节点的度定义为该节点与网络中其他节点之间相互连接的边的数目。一般情况下，度值越大的节点在整个网络中所起的作用就越大，该节点则越重要。因此，可以用度ki来衡量节点i在网络中的重要程度：

(1)

其中当路径l包含节点i，即有边相连接时，δl为1；否则，δl为0。

而度分布则体现出网络中一种重要的几何性质，用分布函数P(k)来表示，代表网络中一个任意选择的节点正好有k条边的概率，即度为k的节点占总节点数的比例。下面我们从两类不同节点的角度研究网络的统计性质。

2.1 线路节点的统计性质

我们首先考虑宝鸡公交线路节点，由于每条公交线路都经过了多个公交站点，因此，线路节点的度即代表其经过的站点数目。图2绘出了每条线路与其经过的站点数的对应情况：横坐标n1代表线路的编号(按节点的度值大小呈降序排列)；纵坐标k1则代表该线路节点的度值，即经过的站点数目。

通过对线路节点经过的公交站点的信息进行统计分析，可以得到以下结论：

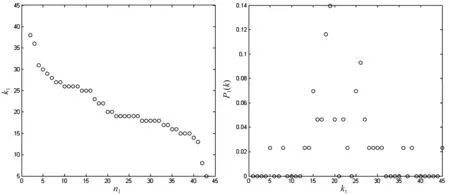
图2 线路节点度值(左)及其度分布(右)

(1)线路节点中具有最大度值的是15路公交线路(k1=45)，占全部公交站点的13.08%,。15路车从宝鸡市区的最东边虢镇到宝鸡火车站，实行分段计价有人售票模式。横跨宝鸡市三区中的陈仓区和金台区，途中经过火车站、金陵桥西、宝鸡石油机械厂、解放区第三医院、行政中心等45个站点，这些站点包括宝鸡市的枢纽站点、宝鸡市的大型厂区以及宝鸡市的繁华地段，是宝鸡交通网络中不可或缺的一部分。线路节点中具有最小度值的是19路公交线路(k1=5)，仅占全部公交站点的1.45%，是去大唐秦王陵的一条特定公交线路。

(2)宝鸡公交线路的平均度为22，经过站点特别多的线路以及特别少的线路仅有少数，大部分线路经过的公交站点数集中在平均值附近，远离平均值的线路数非常少，度值分布较为均匀，呈现出一种泊松分布状态，如图2(右)所示 。这与交通网络的实情较为符合，大部分线路在规划的时候经过的路程远近相对均匀，只有少数线路经过最多的站点，覆盖范围较大，同时具有一两条特定公交线路经过的站点最少。

2.2 站点节点的统计性质

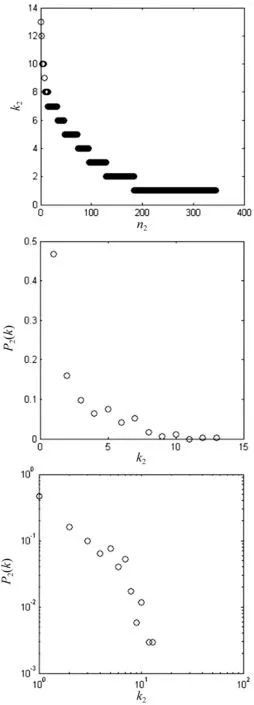
图3 公交站点的度值(左)、k-P(k)度分布(中)以及log-log双对数度分布(右)

下面从公交站点的角度研究宝鸡公交二分图的性质。每个站点都有一条或多条线路经过，因此，站点节点的度即代表经过其线路的数目。图3刻画了每个站点节点与线路数目的对应情况：横坐标n2表示站点节点的编号(按度值的大小呈降序排列)；纵坐标k2为站点节点的度值，即所经过的公交线路的数目。

通过对公交站点所经过的公交线路的信息进行分析，我们得到以下结论：

(1)只有少数站点具有较高的度值，而大部分站点节点的度值仅为1或2。这表明大部分站点均只经过了一条或两条公交线路，只有极少数的站点经过较多的公交线路。这些极少数的公交站点即为宝鸡市的枢纽站点或者主要换乘点。

(2)站点节点中具有最大度值的站点是火车站(k2=13)，表明这个站点经过了最多13条公交线路，即是宝鸡市的枢纽中心，又是宝鸡市区的主要换乘点。宝鸡火车站是铁道部所规定的全国44个大站之一，是连接西北、西南地区的交通枢纽，为陕西省的第二大客运火车站，客流量密集。因此，在交通规划时这里具有最多的公交线路，以便满足宝鸡市不同去向的客流的需求。

(3)随着公交线路数值的减少，站点节点数目呈现快速增长，大多数站点节点的度值很低，只有少数站点具有较高的度值，初步判定这种度值分布情况符合幂律度分布的特性。因此，我们对公交站点的度分布进行统计，宝鸡公交二分图中站点节点的度分布如图3(中)所示，在双对数坐标下可以拟合为一条直线，如图3(右)，其度分布结果符合幂律分布。

2.3 两类节点的对比讨论

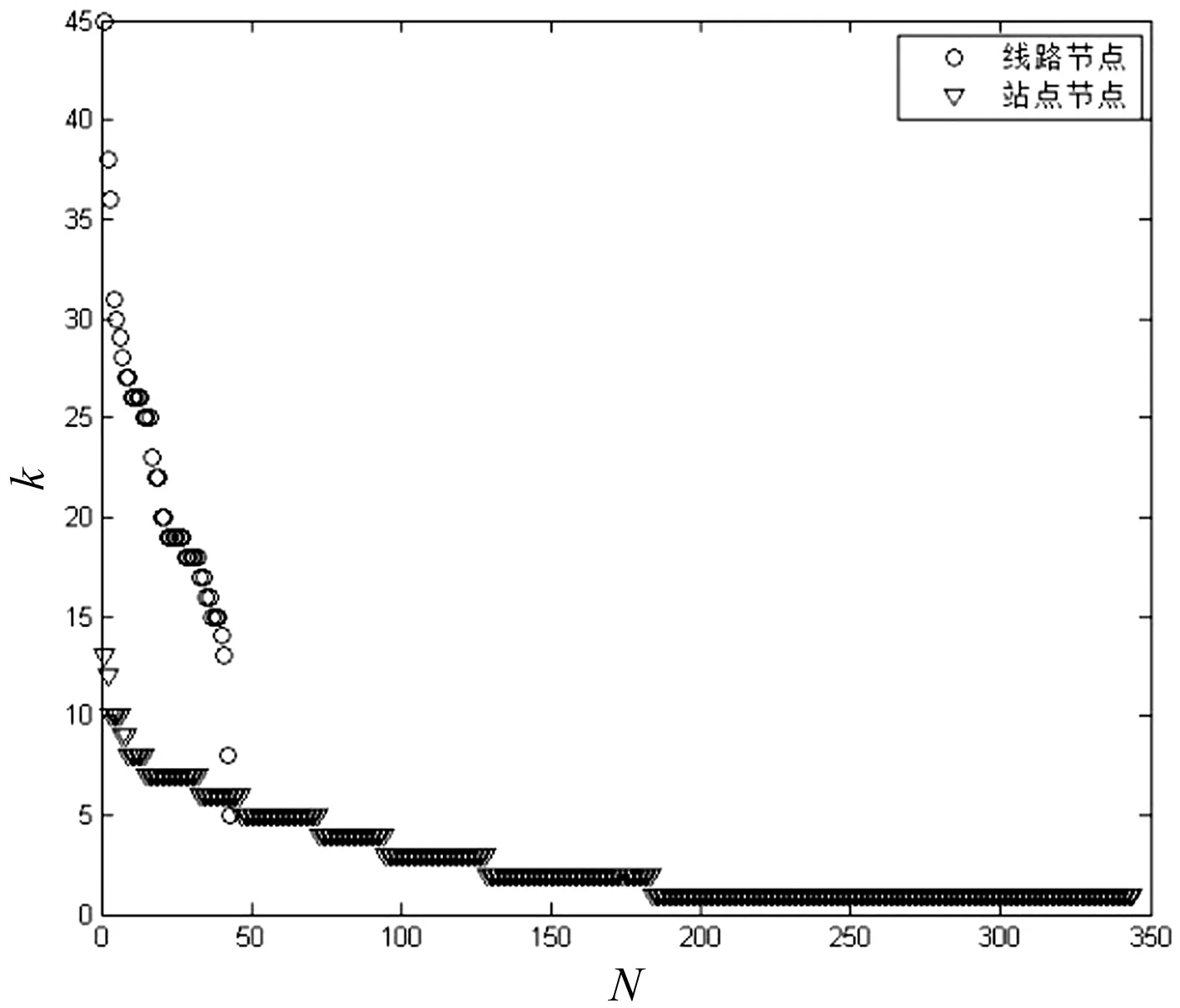
图4 宝鸡公交二分图中，线路节点(圆圈)与站点节点(三角)度值的对比

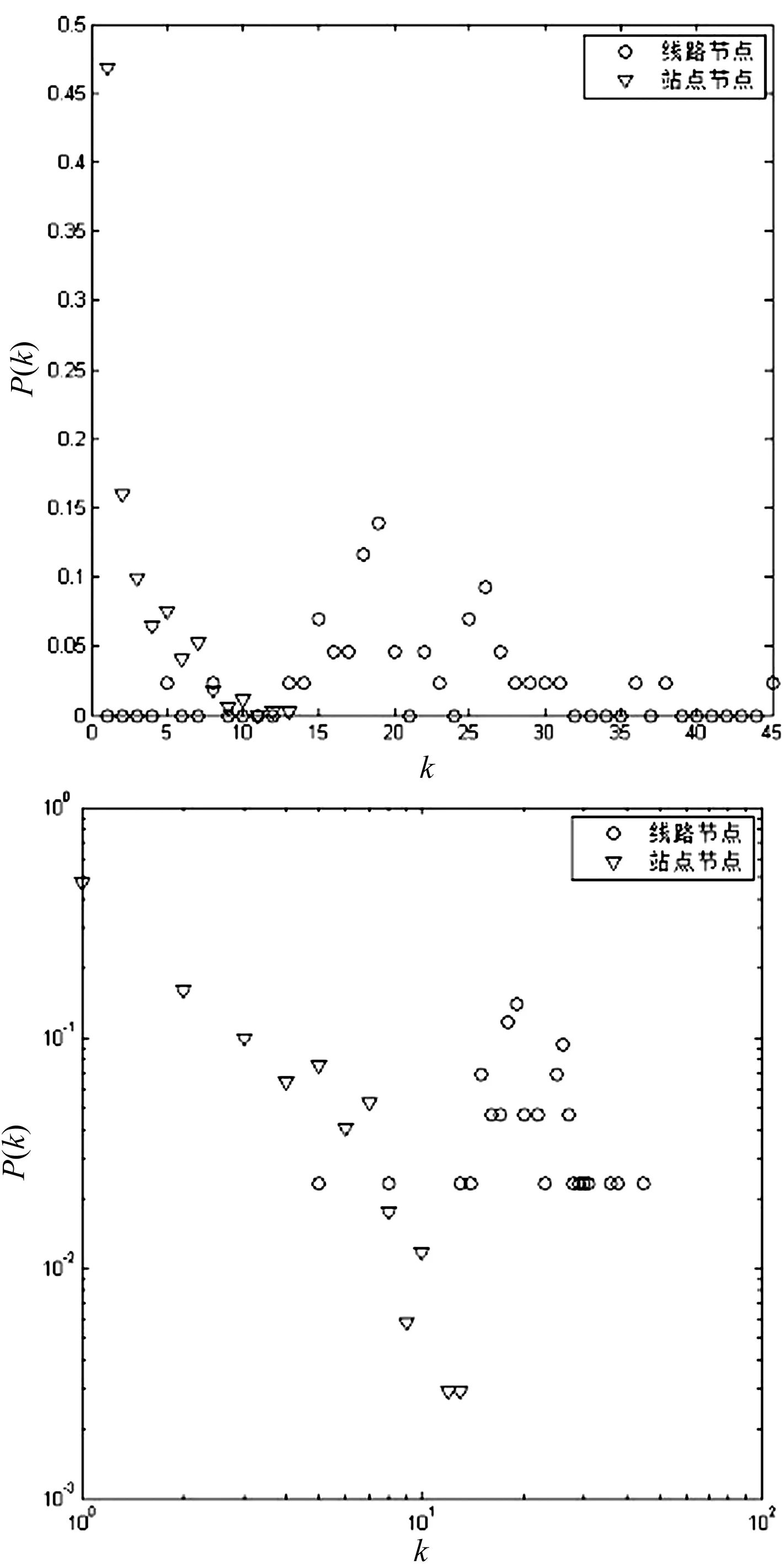
图5 宝鸡公交二分图中，线路节点(圆圈)与站点节点(三角)度分布的对比：k-P(k)度分布(左)以及log-log双对数度分布(右)

宝鸡公交二分图中包含两类不同的节点，由网络的构建规则可知这两类节点的度也代表不同的含义。下面，我们在同一坐标系下对比两类节点的度值及其分布情况，分别如图4和图5所示。图4中，线路节点(圆圈)和站点节点(三角)都是按度值降序排列，两类节点的度值变化明显不同，因此，在图5的度分布对比图中，线路节点呈现出泊松分布，而站点节点呈现出幂律分布，这种不同的分布情况符合交通网络的实际规划。

表2列出了度值排名前5的线路节点和排名前10的站点节点的度值及其占最大可能度值的百分比。表中，15路公交线路的度值最高为45，表明其经过了总共N2=344个站点中的45个站点，比例为13.08%。同理，站点节点中，火车站的度值最高为13，表明13条公交线路经过了火车站，占N1=43条总线路数的30.23%，这些站点都是宝鸡市的主要换乘点、旅游景点或者连接南北东西的枢纽地段。

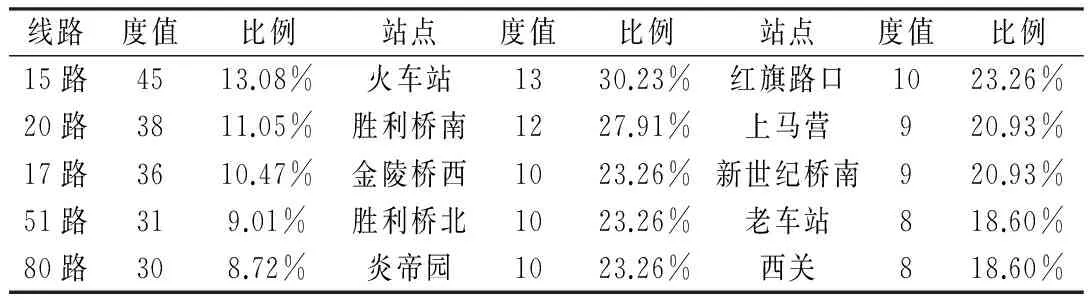
表2 宝鸡公交二分图中，度值排名前5的线路节点与排名前10的站点节点

3 结束语

本文将宝鸡市公交线路信息与公交站点信息结合在一起，构建了宝鸡市公交二分网络模型，运用复杂网络理论进行分析，得出以下结论：

(1) 在宝鸡市公交二分网络中，包含公交线路与公交站点两类不同节点，只有不同类型的节点之间存在连边。研究结果表明，线路节点度分布呈现泊松分布，度值集中在平均值附近，而站点节点度分布极为不均，大部分节点度比较小，极少数节点发挥着重要的作用，度分布均符合幂律分布形式，反映了公交网络的复杂性。

(2) 少数站点具有较高的度值，这些站点有较多的公交线路经过，是宝鸡市的枢纽站点、主要换乘点以及重要景区。这和宝鸡市的实际公交规划相符合。

(3) 大部分公交线路经过的站点数多集中在平均度值左右，具有较多站点和较少站点的公交线路都不多，这些线路覆盖了宝鸡市的较大范围或者是特定旅游线路。

交通系统是一个非常复杂的系统，复杂网络理论的发展为研究交通系统提供了有效的理论工具。我们可通过构建交通网络模型，与实际市区的交通情况相结合，为宝鸡市区的交通规划提供一定的理论指导，综合考虑客流的分布，运行里程的覆盖范围等，以优化公交线路的规划以及公交站点的合理分布。

[1] STROGATZS H. Exploring complex network [J]. Nature, 2001, 410(6825): 268-276.

[3] COSTA L DA F, OLIVEIRA O N JR, TRAVIESO G, et al. Analyzing and modeling real-world phenomena with complex networks: a survey of applications [J]. Advances in Physics，2011, 60(3): 329-412．

[4] M CHORAS,R KOZIK. Real-Time analysis of non-stationary and complex network related data for injection attempts detection[J].Soft Computing in Industrial Applications,2014,(223):257-264.

[5] M NOSRATI,R KARIMI, M Mohammadi,et al. A quick survey on biological networks[J]. World Applied Programming, 2013,3(2):47-51.

[6] 赵金山，狄增如，王大辉．北京市公共汽车交通网络儿何性质的实证研究 [J]．复杂系统与复杂性科学，2005，2(2): 45-48．

[7] 汪涛，吴琳丽．基于复杂网络的城市公交网络抗毁性分析[J]．计算机应用研究，2010，27(11): 4084-4086．

[8] DOROGOVTSEV S N, MENDES J F F. Evolution of networks[J]. Advances in Physics, 2002, 51 (4): 1079-1187.

Modeling and Analysis of Baoji Bus Line-station Network Based on the Bipartite Network

Wang Huana, Hu Jingbob

( a. School of Computer, b. School of Electronic and Electrical Engineering of Baoji University of Arts and Sciences, Baoji Shaanxi 721016, China)

Complex network theory has become an effective tool for studying transport systems. Based on the data about 43 bus lines and 344 bus stations in Baoji City, Shaanxi Province, we have constructed a bipartite station-line public transportation network and analyzed the statistical properties of the network. Research results show that the line node degrees of the network are in Poisson distribution and most of them are concentrated near the average value. However, the station node degrees are in power-law distribution, and a small number of nodes are densely connected as key hub nodes of the network. These densely connected lines and stations can be screened out as key planning objects in the course of investigation of the transportation network in Baoji Cit.

complex network； bipartite graph； public transport network； degree distribution； hub node

10.3969/j.issn.1000-3886.2016.03.008

N949

A

1000-3886(2016)03-0023-03

王欢(1981-)，女，陕西人,讲师，主要从事复杂网络建模及应用研究； 胡静波(1979-)，男，河南人,讲师，主要从事机器视觉及嵌入式系统研究。

定稿日期: 2015-08-31