基于行向S变换的布匹图像疵点检测方法*
赵翠芳, 秦悦桐, 黄学优, 张长江
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
基于行向S变换的布匹图像疵点检测方法*
赵翠芳, 秦悦桐, 黄学优, 张长江
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
受光照条件影响,实际生产车间采集的布匹图像中,其疵点和纹理背景差异不明显,现有的布匹疵点检测方法适应性较低.为提高疵点检测率,提出一种基于行向S变换的布匹疵点检测方法.首先,通过分析周期性纹理布匹图像在行方向上的S变换系数特点,确定布匹纹理频率,去除规则性纹理,只剩下疵点和干扰部分;然后,采用阈值分割,提取疵点信息;最后,根据疵点面积特性判断布匹是否存在疵点,得到最终检测结果.实验结果证明算法的可行性和有效性.
布匹疵点;S变换;阈值分割;纹理结构
布匹疵点是影响布匹质量的主要因素.传统的疵点检测主要靠人工完成,随着大规模集成电路及图像处理技术的不断发展,基于机器视觉的布匹疵点检测系统成为研究热点.
特征提取是基于机器视觉的布匹疵点检测算法的关键,良好的特征能较强地区分正常纹理与各类型疵点.现有的特征提取方法主要依据布匹的纹理形状,大致可分为3类:统计学法[1]、模型法[2]和光谱法[3].统计学法主要刻画布匹的整体纹理特性,对疵点细节信息的刻画能力较差,适合于检测全局疵点或有明显几何特征的疵点,且一般计算量较大.模型法是用一种模型对特定的纹理进行描述,其参数决定了纹理的特性,且受图像亮度变化影响大,对细小的疵点检测效果不佳.光谱法在频域上对布匹图像进行分析,完成疵点检测.Bodnarova等[4]比较了几种常见瑕疵检测方法,如空间灰度共生矩阵、互相关、纹理斑点检测和光谱检测.比较发现,光谱方法应用最广泛,它运用的技术主要有傅里叶变换[5]、小波变换[6]和Gabor滤波[7],速度快,效率高.
本文试图将一种较新的时频分析方法——S变换引入到布匹纹理疵点检测中.加拿大学者Stockwell等[8]于1996年提出的S变换集中了短时傅里叶变换和小波变换的优点,具有较高的时频分辨率,是一类有效的信号分析处理方法.近年来,人们对其在各个领域的应用也越来越多,目前主要应用于地震信号分析[9]、电能质量分析[10]和信号降噪处理[11]等领域.
1 S变换原理
S变换可以表示成加时窗傅里叶变换.函数h(t)的S正变换表示为[8]
(1)
式(1)中:S是h(t)的S变换;f为频率;τ和t是时间,其中τ控制时间轴上高斯窗的位置.
S变换中的窗函数必须满足归一化条件,即
(2)
(3)
式(3)中:m为频移因子离散序号;n为频率值的离散序号;j为τ的离散序号;j,m和n=0,1,2,…,N-1;T为时间采样间隔.
S反变换为
(4)
利用傅里叶反变换可以实现离散S反变换式,即
(5)
2 确定织物周期性纹理频率
纹理是物体表面的固有特征之一,也是图像区域一种重要的属性.在进行布匹疵点检测过程中,如果能够去除织物固有的周期性纹理,就能增强疵点信息,有利于疵点检测.
在实际布匹生产车间中,以机器顶部前方横梁上的日光灯作为布匹表面的照明条件,将分辨率为1 290×960的面阵摄像机架在横梁上进行图像采集.摄像机的帧频为30fps,视场长边负责0.9m的布匹实际幅面区域,精度为1.44像素/mm.为减少仿真图像的计算量,从采集的原始无疵点布匹图像中截取图像,分辨率为256×128,如图1(a)所示.又从图1(a)中抽取某一行信号,如图1(b)所示.可以看出,布匹纹理图像的灰度值在行方向上基本呈周期分布.

(a)原始布匹图像 (b)从(a)图中抽取的某行信号图1 布匹纹理结构
图2(a)为正弦信号模型y=sin(2πt),在Matlab中仿真时选取采样点数为200,采样频率为10;图2(b)为正弦信号y在S变换域内的时频图.图2(b)中颜色越明亮,表示S变换系数模值越大.可以看出,正弦信号y的S变换系数在各频率点的模值明亮区域集中,且呈一条直线.
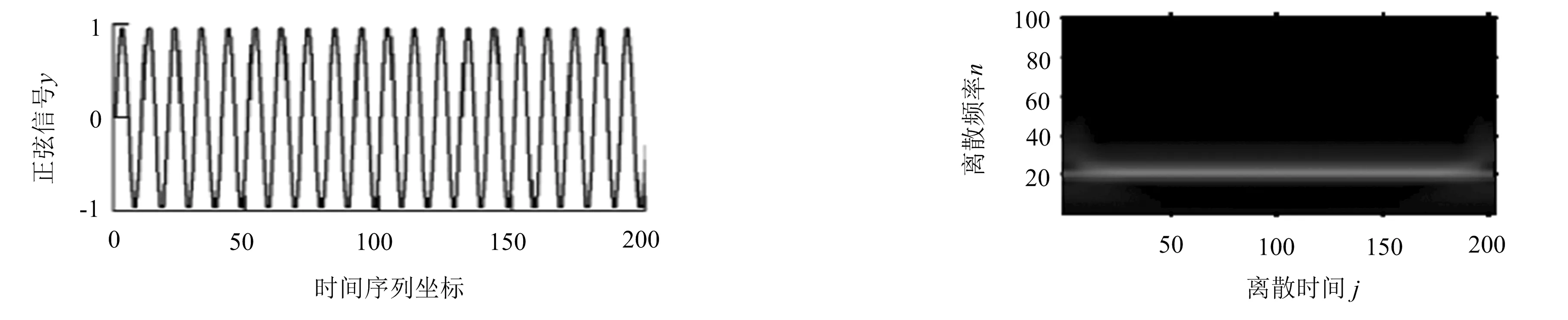
(a)正弦信号y波形图 (b)正弦信号y的S变换域时频分析图图2 正弦信号y的S变换分析
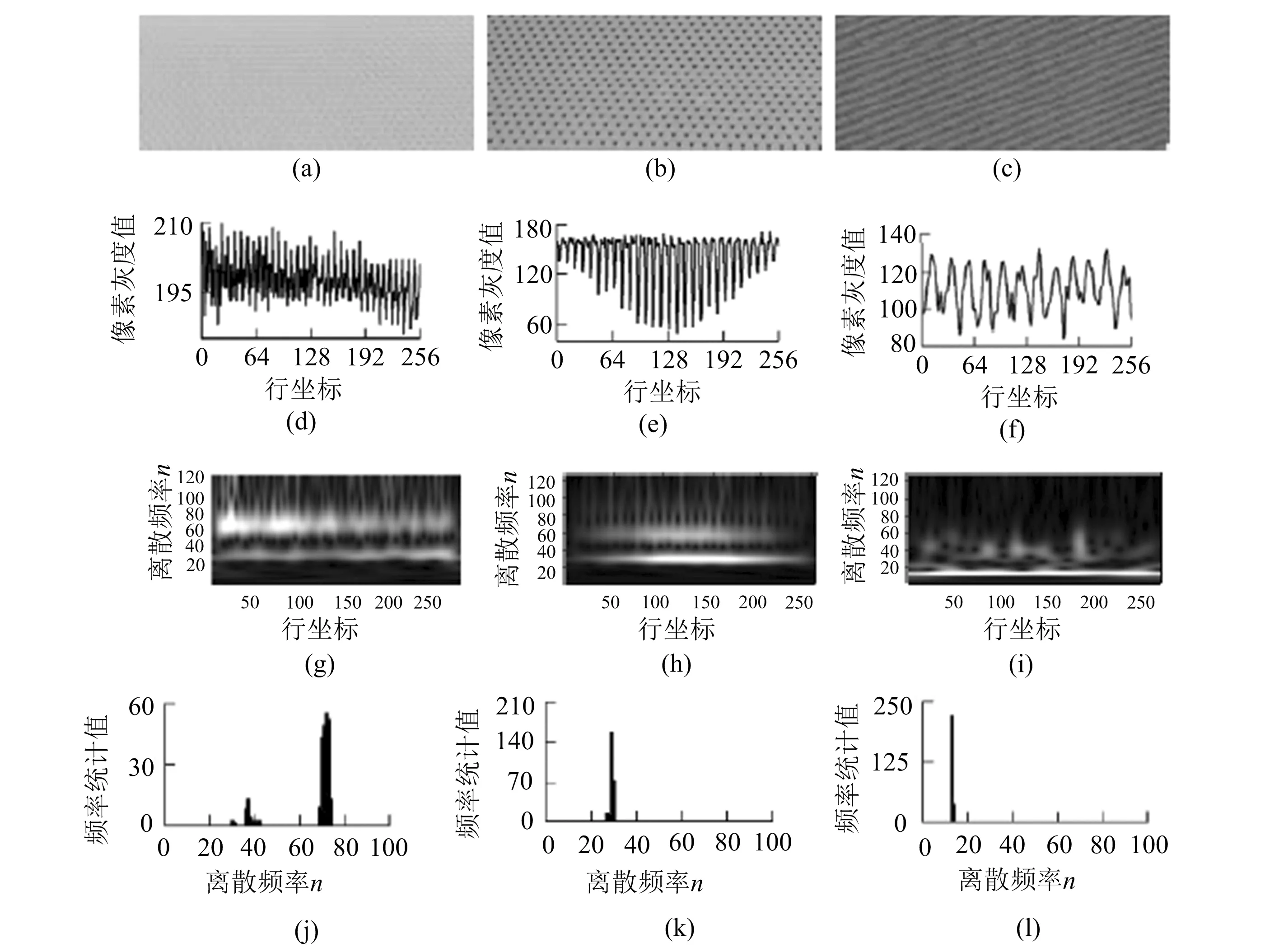
(a)~(c)为原始无疵点布匹图像;(d)~(f)为从图(a)~(c)中抽取的某行信号;(g)~(i)为信号(d)~(f)的S变换域时频图;(j)~(l)为对应时频图(g)~(i)的模最大值频率统计直方图图3 布匹图像纹理结构分析
图3(a)~图3(c)分别为实际场景中采集的3种不同类型的原始无疵点布匹图像;图3(d)~图3(f)分别为从图3(a)~图3(c)所示布匹图像中抽取的某行信号;图3(g)~图3(i)分别为图3(d)~图3(f)所示信号在S变换域内的时频图;图3(j)~图3(l)分别为图3(g)~图3(i)所示时频图的模最大值频率统计直方图.分析图3(g)~图3(i)可知,对于周期性布匹纹理信号,其S变换域内系数模最大值相对比较集中,与正弦信号一致,呈直线.可见模最大值频率直方图均呈现为单波峰或双波峰状,且双波峰中两峰差距显著.由此可以把直方图中最高波峰所对应的频率点确定为纹理信号频率,从而得出布匹纹理频率fT.
3 疵点检测
3.1 S变换去除布匹纹理信号
规整的布匹图像往往是有规律的纹理图像,疵点的发生破坏了图像局部区域的纹理完整性.由于疵点是不经常发生的,即疵点出现频率比纹理频率低,所以在S变换域,疵点信号相对于周期性纹理信号存在于低频区域.设置合理的低通滤波器,将频率满足f≥fTheld(fTheld为频率阈值)的S变换系数去除,频率满足f 图4(a)~图4(c)为实际场景中采集的布匹疵点图像;图4(d)~图4(f)为从图4(a)~图4(c)布匹图像中抽取的某行带疵点信号;图4(g)~图4(i)为图4(d)~图4(f)中抽取信号的S变换域时频图;图4(j)~图4(l)为去除纹理和干扰后的信号F.观察图4(d)~图4(f)带疵点信号波形图可知,受光照条件和噪声干扰的影响,从幅度上看,纹理背景所在的大部分信号幅度波动较大,疵点被淹没在纹理背景中.从图4(j)~图4(l)去除周期性纹理后的信号F的波形图可以看出,经过S变换处理后,疵点与背景的幅度差异明显增强. (a)~(c)为原始无疵点布匹图像;(d)~(f)为从图(a)~(c)中抽取的某行信号;(g)~(i)为信号(d)~(f)的S变换域时频图;(j)~(l)为对应时频图(d)~(f)去除周期性纹理后的信号图4 提取疵点信号 3.2 信号阈值分割 采用S变换去除布匹周期性纹理后,布匹图像中存有潜在疵点和部分噪声干扰.对S反变换信号图像F进行阈值分割,进一步提取疵点信息.分割阈值T采用Niblack算法进行确定: (6) 式(6)中:m为信号F的平均值;S为信号F的均方差;λ为经验值,一般选择3~5,这里λ取3. 3.3 疵点判别 将原始布匹图像的每行数据进行S变换处理,并进行阈值分割,得到分割图像.由于提取疵点信息过程中存在干扰信号,为减少误判,结合连通区域面积特征进行疵点判别.根据实际机器视觉平台的摄像头参数及实际拍摄的布匹幅面区域宽度,可统计单纱线所成像素个数为N.当局部连通区域面积大于等于N时,就认为有疵点存在,否则疵点不存在.布匹断丝疵点的宽度一般在2 mm以上(根据工厂统计,纹理最细的布匹其断线疵点的宽度不会小于2 mm),若以2 mm作为最小识别精度,则根据系统实际采集图像情况(1.44 像素/mm)确定N的值,这里设N为3. 为验证算法的有效性,选取TILDA数据库和实际场景中采集的不同类型的500幅布匹疵点图像进行Matlab仿真实验,并与文献[7]中提到的Gabor滤波方法进行比较.图5为原始疵点图像(包括污点和断线疵点),图6为采用本文提出的算法对布匹图像进行疵点检测的分割结果,图7为Gabor滤波算法疵点分割结果.可以看出,本文提出的算法相比Gabor滤波器算法[7]效果较好.利用本文算法能较准确地分割出布匹疵点位置.Gabor滤波器通过疵点边缘增强效应分割疵点位置,这种方法取决于滤波器带通区域内2种纹理成分(织物和疵点)能量之差,其值越大,边缘增强效果越好,越利于疵点分割.当织物与疵点能量差别不大时,利用Gabor滤波就很难检测出疵点. 从左到右、从上到下分别为:疵点图像1~疵点图像9图5 原始疵点图像 为客观评价疵点分割算法的性能,采用传统的图像分割评价参数(如式(7)所示)来衡量,得到的结果如表1所示. 图6 本文提出算法的分割结果 图7 Gabor[7]算法分割图像 J本文方法Gabor变换算法疵点图像10.54120.3297疵点图像20.46090.2345疵点图像30.23760.2539疵点图像40.34070.2432疵点图像50.32210.0988疵点图像60.06780.0033疵点图像70.48930.1570疵点图像80.25640.0028疵点图像90.29950.0056 (7) 式(7)中:Ud为从同一种疵点类型在多个疵点区域中计算出的某一特征的平均值,能表示出该疵点区域与正常纹理之间的差异;Um为从大量正常纹理区域中计算出的该区域特征值的平均值;J为疵点区域与非疵点区域特征值均值的比值.Kumar等[12]也是采用类似的比值方法评估疵点分割算法的分割能力.如果得到的值较大,就表明疵点区域与非疵点区域特征值之间具有较大的欧式距离,分割性能较好.观察表1可见,本文提出的疵点分割方法计算所得的值大多优于Gabor变换算法. 本文以实际场景中采集到的布匹图像为研究对象,提出一种基于行向S变换的布匹疵点检测方法.S变换作为短时傅里叶变换和小波变换的扩展,具有频率分辨率高、抗噪性强的优点.利用S变换能有效地去除周期性纹理,有利于疵点信号的提取,且不易受织物和疵点的能量差别、光照条件、噪声等影响.S变换可以借助FFT和卷积定理实现快速计算.此外,S变换是一个线性运算,满足线性叠加原理,且具有无损可逆性.这两个性质为本文的检测算法提供了良好的基础,有利于算法在实际工程中实现. [1]Bu H G,Wang J,Huang X B.Fabric defect detection based on multiple fractal features and support vector data description[J].Eng Appl Artif Intel,2009,22(2):224-235. [2]Bu H G,Huang X B,Wang J,et al.Detection of fabric defects by auto regressive spectral analysis and support vector data description[J].Text Res J,2010,80(7):579-589. [3]Li G X,Li Y F.Defect detection study of fabric based on gabor filter algorithm[J].Mater Sci Forum,2011,697/698:491-494. [4]Bodmarova A,Bennamoun M,Kubik K K.Suitability analysis of techniques for flaw detection in textiles using texture analysis[J].Formal Pattern Analysis & Applications,2000,3(3):254-266. [5]Casterllini C,Francini F,Longobardi G,et al.On-line textile quality control using optical Fourier transform[J].Opt Laser Eng,1996,24(1):19-32. [6]Yang X,Pang G,Yung N.Discriminative training approaches to fabric defect classification based on wavelet transform[J].Pattern Recogn,2004,37(5):889-899. [7]杨晓波.基于Gabor滤波器的织物疵点检测[J].纺织学报,2010,31(4):55-59. [8]Stockwell R G,Mansinha L,Lowe R P.Localization of the complex spectrum:The S transform[J].IEEE T Signal Process,1996,44(4):998-1001. [9]马见青,李庆春,王美丁,等.广义S变换在地震勘探中的研究进展[J].物探与化探,2011,35(2):265-269. [10]Reddy M J B,Raghupathy R K,Venkatesh K P,et al.Power quality analysis using discrete orthogonal S-transform (DOST)[J]. Digit Signal Process,2013,23(2):616-626. [11]李兴慧,张光明,阴俊霞,等.基于S变换的自适应降噪方法[J].兰州理工大学学报,2013,39(2):21-24. [12]Kumar A,Pang G K H.Defect detection in textured materials using optimized filters[J].IEEE T Syst Man Cy B,2002,32(5):553-570. (责任编辑 陶立方) Fabric defect detection with line-based S-transform ZHAO Cuifang, QIN Yuetong, Huang Xueyou, ZHANG Changjiang (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China) Affected by the lighting conditions, there had no significant difference between defect and texture background in the fabric images from the actual production workshop. So the existing fabric defect detection methods had low adaptability. To improve the detection rate, a novel fabric defect detection algorithm with one-dimensional S-transform on the line direction was proposed. Firstly, based on the S-transform with high time-frequency resolution, it was analyzed the characteristics of the periodic texture images S-transform coefficients, determined the frequency of fabric texture, removed the image regular textures, and then only preserved the defects and interference regions. Secondly, it was detected the defect by using threshold segmentation. Finally, based on the area characteristics, it was determined whether the image had defects. Experimental results was given to demonstrate the feasibility and effectiveness of the algorithm. abric defect; S-transform; threshold segmentation; texture structure 10.16218/j.issn.1001-5051.2016.04.006 2015-12-09; 2016-06-16 浙江省科技厅公益性技术应用研究计划项目(2012C31005);浙江省重中之重学科“计算机科学与技术”资助项目 赵翠芳(1979-),女,副教授,博士.研究方向:机器视觉;目标检测与识别;数字图像处理;高速信号处理. TP751.1 A 1001-5051(2016)04-0392-07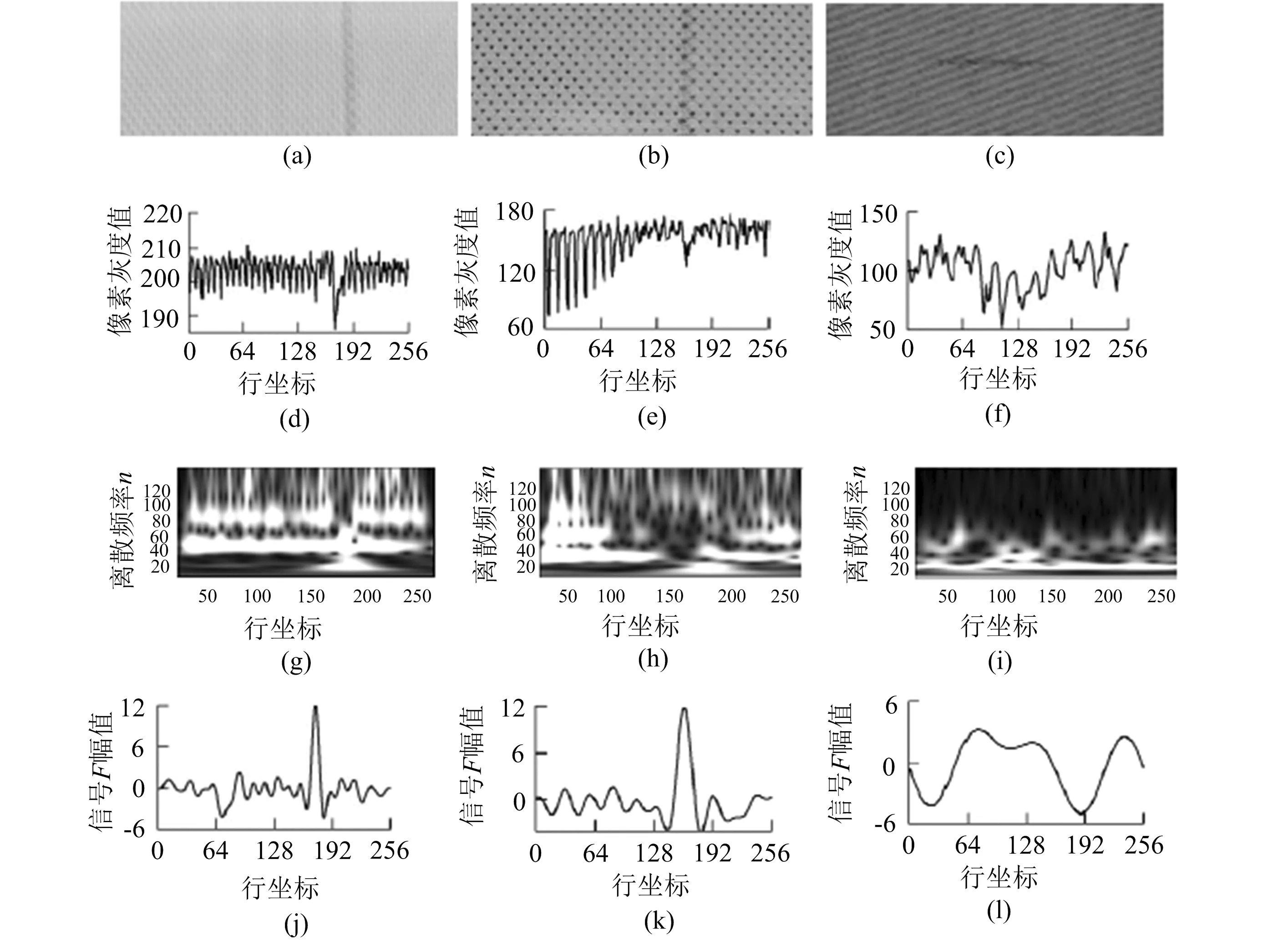

4 实验结果及分析



5 结 语

