ICP算法在计算机辅助肝脏手术空间配准中的应用价值
赵 挺
ICP算法在计算机辅助肝脏手术空间配准中的应用价值
赵 挺
在计算机辅助肝脏手术中,医学图像与实际空间之间的配准问题是目前社会所关注的重点部分,针对计算机辅助肝脏手术空间配准技术中的术前CT图像和手术过程中的实际空间进行配准的问题,提出一种基于ICP算法的手术空间配准技术,并且集合相关算法性能仿真,来对ICP算法在计算机辅助肝脏手术空间配准中的应用价值进行分析。
ICP算法;计算机辅助肝脏手术;空间配准
1 概述
在计算机辅助肝脏手术中,其中空间的配准问题是手术中的重要部分,术前若能进行精确空间配准,医师便能确定病灶具体位置,根据患者实际情况选择最佳手术方案,且可对手术过程中由于患者个体差异而引起的风险因素进行综合考虑,最大程度地降低手术风险,使整个手术过程更加安全可靠[1-2]。
2 空间配准算法
空间配准算法对于临床医学来说较为重要,通过CT空间与实际手术空间相互结合,能够在一定程度上提高手术的精准程度,帮助医师避开重要组织结构,进行安全可靠的手术[3]。对空间配准算法在计算机辅助肝脏手术中应用价值的研究已有十多年了,但是由于使用配准技术时,术前需要使用精确
扫描设备对患者进行扫描,并且需结合相关手术设备来对患者的影像资料进行处理。手术设备和扫描设备的精确程度均会对配准效果产生一定影响,同时也会影响手术的可靠性和安全性。目前,医院所使用的影像设备主要包括CT、磁共振成像(MRI)等,这些技术与图像处理技术相互配合,能够进一步提高空间配准的整体精度。为了使计算机辅助肝脏手术安全顺利实施,需要一种配准计算方法作为支持,本研究在传统ICP算法基础上,提出一种点云ICP拼接算法方案,以此来提高整体的配准精度。
3 基于ICP算法的空间配准技术
3.1 医学图像配准 在临床医学中,图像配准精度是其中较为重要的技术之一,已应用于临床多种手术中,主要是指将图像进行相应空间变化,使其与另外一幅图像中的对应点在空间上保持一致,这样的两种图像主要包括经过影像设备所记录的图像和经过相关处理的患者影像资料。目前,图像配准技术主要应用于计算机辅助医疗中,在进行图像配准过程中,成像模式和成像时间均不同,此时,同一个对象的数据之间存在着相对平移和旋转,在处理不当时,甚至会出现不规律畸形变化,其会影响对患者图像的综合分析,为了提高手术的整体效果,需要对医学图像的配准问题进行解决。
3.2 ICP算法 图像配准基本ICP算法是一种基于纯粹集合模型的三维物体对准的主导性算法,这种算法于1992年提出[4]。由于ICP算法的三维立体特性,常被应用于空间配准计算中,在此过程中,多视对齐可以这样来进行描述:对两个来自不同坐标系的三维数据点集进行定义,然后找出这样两个点集的空间变换,对其确定后,进行相应空间匹配,其中空间第1个点集可以用{Pi丨Pi∈R3,i=1,2...,N},而第2个点集的对齐匹配转换为下式(1),这样可以得出目标函数的最小值。
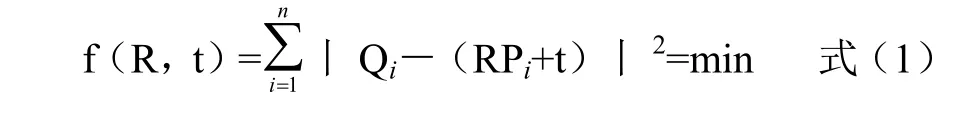
ICP算法其实是一种三维空间图形匹配方法,这种方法是基于最小二乘法进行的,在计算过程中,通过对其中所对应的关系点集进行重复确定,计算出其中最优刚体变换的过程,直至计算出其中的某个点集能够正确匹配到相应的收敛准则才算满足,其主要目的是寻找目标点集和参考点之间的旋转R和平移T的相互变换,在寻找过程中,需要使这两组匹配数据中间满足某种程度度量准则下的最优匹配值,一般情况下,目标点集可以表示为:,而其中的参考点集可以表示为,而在第k代中计算与点集P的坐标,其中所对应的坐标为在这样的几个对应点集中,可以对P和Qk之间的变换矩阵进行计算,并且对原变化进行相应的更新,这样的计算一直持续到数据之间的平均距离小于给定阈值,其具体步骤体现在以下几个方面[5-7]:①以确定目标点集为P,在P中对点集的范围进行确定,取点集Pik∈P;②对参考点集Q中对应点Qki∈Qk进行计算,并且使丨Qik-Pik丨=min;③对旋转矩阵Rk和平移向量Tk进行计算,使最后的结果满足
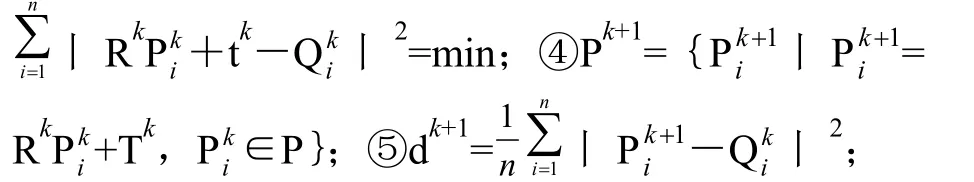
⑥在计算的过程中,如果其中的dk+1大于或者等于给定的t值,那么重新返回5式中进行计算,直到dk+1<t为止。
4 对ICP拼接算法进行改进
在对图像进行配准过程中,需要根据不同视角下的两组数据点云,来对其中每点的曲面法矢量和曲率进行计算,并且由其中曲率保持一致的点来构成配对点,以此来对其中每个点对应的法矢量方向一致的三维空间转换进行计算,然后需要对计算结果进行筛选,一般情况下,可以采用几何哈希法来筛选出最佳的三维变换,然后用此变换作用于整个点云,以此来完成整个点云的拼接。在对ICP算法进行改进的过程中,主要是对其中的最近点选取方法进行改变,然后对点云进行再次拼接,在此种情况下,可确保两组点云之间拼接的精确性[8]。对于两组点云来说,需要在不同的视野下对其中每点的曲率和法矢量进行计算,根据实际计算结果,对初次的拼接转换进行计算。
4.1 对点云的法矢量进行计算 对于两组点云的法矢量计算,首先需将两组点云视为A和B,在A中选取任意一点ai,并且对其中k个临近点Xj进行搜寻和选择,一般情况下,j值大于等于1,小于等于k,这些临近点共同构成邻域U(ai),接下来可以使用最小二乘法将U(ai)中所有的点拟合成相应平面,这样的平面就可以被看成点ai的近似切平面,在U(ai)中,行心可以被记为Oi,其单位法矢量被记为ni,在这种情况下,构造U(ai)协变矩阵M的计算公式为:

在M中,其最小特征值对应的特征向量为ni,接下来可以利用传播法来对法矢量进行调整,在此种情况下,可以将两组点云中的法矢量指向曲面外向。
4.2 对点云的曲率进行计算 点云A中任意一点ai,并且以ai为原点,以ni的单位向量为w,u为最小=选乘法中邻域中的点,v为点云中欧式距离近的点,建立相应的局部右手坐标系(ai-uvw),而U(ai)中的点Xj在此坐标系中的实际坐标可以表示为(ui,vi,wi),由k个邻近点,可以得出以下曲面方程:

在这个方程中,可以采用最小二乘法来对其进行求解,最后得出的结果为曲面方程S(u,v),并且可以根据曲面第1、第2基本公式,可以对点ai处的主曲率k1(ai)、k2(ai)进行计算,计算公式如下:
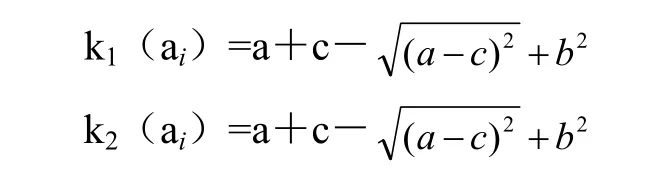
4.3 对配对点云进行拼接 在对不同视野下点云的主曲率进行计算后,点云A中每个点ai∈A,在点云B中寻找所有与ai曲率相同的点bi,其公式为[9-10]:
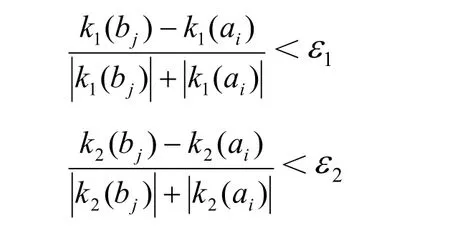
所有曲率相同的点可以构成一个配对点云,记为P和Q,其中P∈A,Q∈B,再利用集合哈希法来对其中最优的三维空间转换进行筛选,便可完成初次拼接。拼接完成后,配对点云具有极为相近的初始位置,并且用配对点云来对拼接变换进行计算,但是在计算过程中,需要考虑其中的误差,一般情况下,以p为目标集中点,q为其中的参与点,不同视野下点云的拼接误差定义为:

5 算法性能仿真
以肝脏模型作为试验对象,在进行试验前需进行CT检查,检查所用设备为GE MEDICAL SYSTEMHISpeed螺旋CT设备,其操作系统为Windows XP,内存为1G,本研究所采取的预处理配准ICP算法与普通ICP算法以及本研究的拼接算法进行配准误差比较结果,见表1。
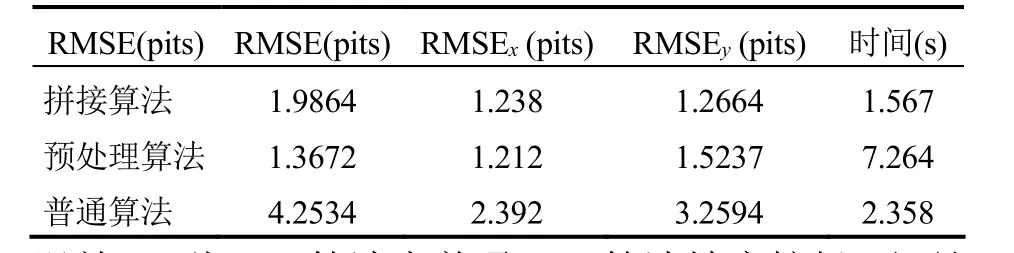
表13 种算法的误差比较
表格中的RMSE是指检测出的特征点坐标与已知特征点坐标之间的整体均方根误差,而RMSEx指X方向的均方根误差,而RMSEy指Y方向的均方根误差,3种ICP算法中普通ICP算法精度较低,但是其计算速度相比预处理法来说较快,而预处理ICP算法精度较高,但速度较慢,而拼接ICP算法算法精度较高,同时速度较快。
在对图像进行配准过程中,需先选取目标图像中的一部分,并且将此图像与参考图像进行叠加,形成相应的叠合图,在进行度量过程中,重复率越高,表明兴趣算子的稳定性越好,满足匹配要求的点也就越多,在通过计算机进行间接图像旋转、平移模拟图像变形后,其中的重复率较高,能够满足计算机辅助肝脏手术空间的配准要求[11-12]。
6 结束语
计算机辅助肝脏手术空间的配准要求精度较高,需要相应的ICP算法来对其中的配准误差进行控制,ICP拼接算法在对其中两组不同视野下的数据点云的曲率进行计算后,利用其中多次的点云拼接计算,其配准误差基本上控制在1 mm以下,具有极高精度,可以应用于实际手术中,以降低手术实际风险。
[1] 韦韫韬,周轶冰.ICP算法在计算机辅助肝脏手术空间配准中的应用研究[J].科技通报,2014(1)∶162-165.
[2] 韦韫韬,周轶冰,周东航,等.基于ICP算法的计算机辅助肝脏手术空间配准技术[J].佳木斯大学学报(自然科学版),2013,31(1)∶116-118.
[3] 韦韫韬,周轶冰,周东航,等.ICP算法在计算机辅助外科手术空间配准中的技术研究[J].科技信息,2012(36)∶637-637.
[4] 韦韫韬.计算机辅助外科手术空间配准技术的研究[J].电脑开发与应用,2013,26(9)∶1-3.
[5] 韦韫韬,周轶冰,周东航,等.四元数在计算机辅助手术空间配准中的研究[J].微处理机,2013,34(4)∶63-65.
[6] 田和强,吴冬梅,杜志江,等.基于ICP算法的脊椎手术导航配准技术[J].华南理工大学学报(自然科学版),2010,38(11)∶141-147.
[7] 杨现辉,王惠南.ICP算法在3D点云配准中的应用研究[J].计算机仿真,2010,27(8)∶235-238.
[8] 向华.手术导航三维空间配准技术研究[D].北京∶清华大学,2012.
[9] 李元璐.基于ICP算法的医学图像配准的研究[D].河北∶河北工业大学,2012.
[10] 孙蕾.手术导航系统中空间配准算法的研究[D].河北∶河北工业大学,2015.
[11] 周春艳,李勇,邹峥嵘.三维点云ICP算法改进研究[J].计算机技术与发展,2011,21(8)∶75-77.
[12] 袁建英,刘先勇,刘伟,等.改进ICP算法实现多视点云精确配准研究[J].传感器与微系统,2008,27(5)∶27-30.
R657.3;TP391.41
A 【DOI】10.12010/j.issn.1673-5846.2016.11.053
辽宁省本溪市医学交流中心,辽宁本溪 117000

