并联柔性机构失谐动态响应分析方法

于霖冲，林志树，林幸燕

(厦门理工学院 机械与汽车工程学院，福建 厦门 361024)



并联柔性机构失谐动态响应分析方法

于霖冲，林志树，林幸燕

(厦门理工学院 机械与汽车工程学院，福建 厦门 361024)

为了探索周期机构在失谐时的非线性动态响应，尤其是柔性机构在失谐情况下高度非线性的运动学和动力学参数动态响应，提出了基于Monte Carlo方法的柔性周期机构失谐动态响应分析方法，以并联机构为例对多种失谐情况进行了动态响应对比分析，初步探讨了失谐量与失谐动态响应变化的规律。结果表明，周期机构普遍存在失谐现象，失谐动态响应与失谐量之间为非线性关系，存在动态响应局部化现象。

并联机构；柔性机构；失谐；动态响应

0 引言

周期机构是指由相同的子机构通过串联或者并联组合形成的机构系统，是子机构和运动副的集合。与周期结构相比，周期机构不但要像周期结构一样在运动过程中保持拓扑结构符合设计要求，而且要完成规定的运动并传递动力。各个子机构完全相同的周期机构为谐调机构，反之，如果子机构之间在几何和物理等参数上存在差异，这种机构为失谐机构。失谐问题的研究始于1958年由Anderson在金属材料凝固物理学领域首次提出[1]，上世纪80年代扩展到失谐结构的研究[2]，并在上世纪90年代取得了突破性进展[3]，我国学者在同期也开始关注失谐结构的研究，并在新世纪初取得了很多重要的成果[4-5]。然而，失谐机构的研究却相对滞后，与周期机构的广泛应用和发展不相匹配，有部分学者开始尝试将失谐结构的研究成果拓展到失谐机构，例如：失谐梁的平移运动实验研究、失谐情况下柔性机构高速运动的随机动态响应，例如：于霖冲探讨了柔性机构在谐调设计的情况下也会发生失谐动态响应[6]。近三十年来发展起来的多体系统动力学解决了周期机构建模以及动力学分析中的很多问题[7]，然而，周期机构失谐分析的理论和方法研究刚刚起步尚在逐步创立完善阶段。本文将周期结构失谐研究成果与柔性多体系统动力学理论方法相结合，建立了并联柔性机构失谐动态响应分析模型，探讨了并联柔性机构失谐动态响应，并提出了失谐响应随机分析方法，为失谐机构进一步研究奠定了基础。

1 并联柔性周期机构模型

周期机构的拓扑构型主要有并联和串联两种组合形式，由失谐振动在周期机构中的传播形式确定的，若振动同时在各个子机构中传播，这种机构为并联机构，如图1所示。

图1 周期机构示意图

1.1 柔性周期机构系统

子机构中包含有柔性构件(长细比大)的周期机构叫做柔性周期机构，记为M。如果M由n个子机构Mi组成，则：

(1)

如图2所示的并联柔性机构，在曲轴上并联了n个连杆滑块子机构，理论上n可以趋近于无穷大。通常将长细比大的构件(如曲轴、曲柄和连杆)按照柔性构件建模，而滑块则按照刚体建模。

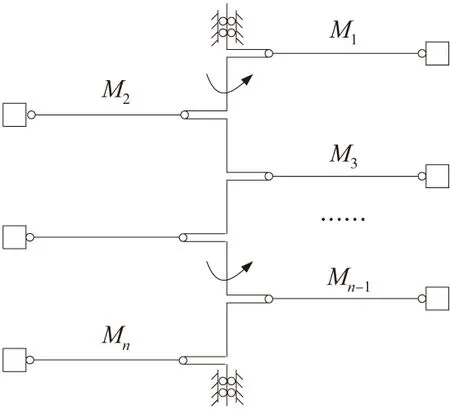
图2 并联柔性机构模型

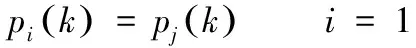
(2)

则，该柔性周期机构为谐调机构。若(2)式对于某个或者某些参数不成立，则该柔性周期机构为失谐机构。

1.2 柔性机构的子机构模型

子机构为曲柄滑块机构，如图3所示。假设细长构件曲轴、曲柄和连杆为柔性构件，而滑块假设为刚体构件。

图3 子机构模型

(3)

即：单位失谐量是参数理想值的1%。

如果子机构之间的失谐量σm为0，即：

σm=0

(4)

则说明构件之间是谐调的，机构为谐调机构。否则，若：

σm≠0

(5)

则说明构件之间是失谐的，机构为失谐机构。

引起失谐动态响应的因素是多样的，动力学参数和运动学参数失谐都可以引起失谐响应，其中质量、动力和摩擦都是常见的可以引起失谐动态响应的因素[8-10]。为了比较谐调和失谐的动态响应，如图2所示在曲轴上依次一一对应对称并联了多个曲柄滑块子机构，用以对比多种情况下的动态响应。通常情况下，刚体假设的谐调机构计算结果作为理想动态响应。

2 柔性机构失谐动态响应分析方法

2.1 质量失谐的动态响应

质量失谐是最常见的失谐影响因素之一，分别将质量失谐量为2.5σ和5σ，以滑块为研究对象，求解滑块的位移并进行比较。质量引起的位移失谐动态响应如图4所示，在图4a中，实线代表谐调动态响应，而虚线代表质量失谐(失谐量为5σ)动态响应。图4中，横坐标为时间，单位为s；纵坐标为位移，单位为mm。

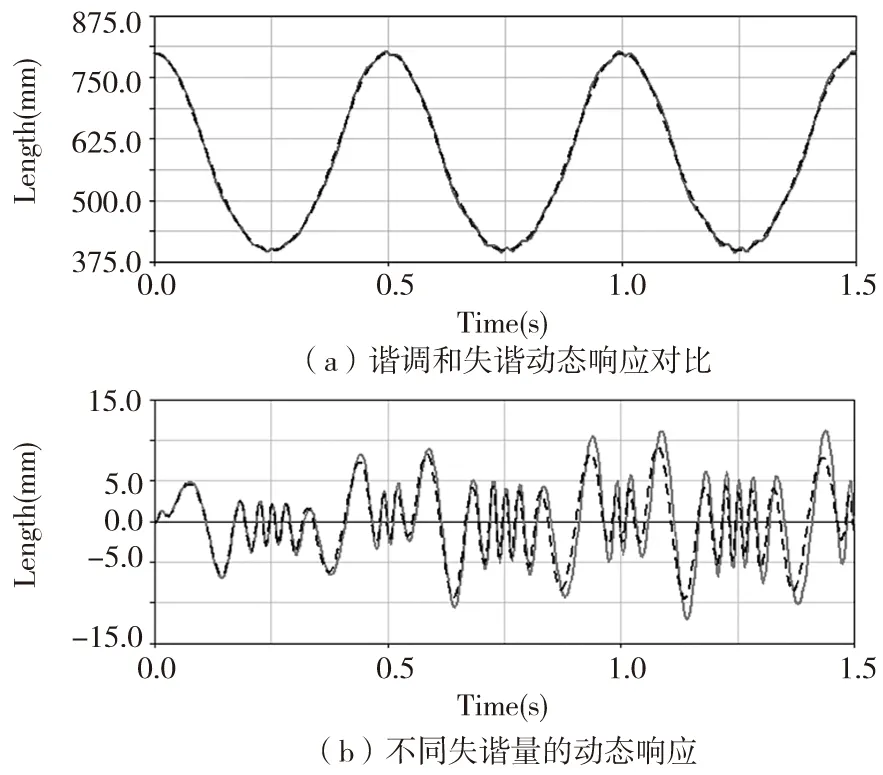
图4 质量失谐动态响应

在图4b中，分别给出了失谐量为2.5σ和5σ的动态响应差，虚线代表失谐量为2.5σ的动态响应，极值达到9.46mm；虚线代表失谐量为5σ的动态响应，极值达到11.94mm。在出现质量失谐时，随着失谐量的增大，动态响应的极值也随之增大。如果只分析有代表性的某一个子机构作为所有子机构的动态响应是有误差的，例如传统的有限元分析方法。

2.2 动力失谐的动态响应

动力失谐带来的影响诸如速度差异、位置精度差异等，也是周期机构中常见的失谐现象之一。由动力失谐引起的滑块速度失谐动态响应如图5所示，在图5a中，实线代表谐调动态响应，而虚线代表动力失谐动态响应。图5中，横坐标为时间，单位为s；纵坐标为速度，单位为mm/s。

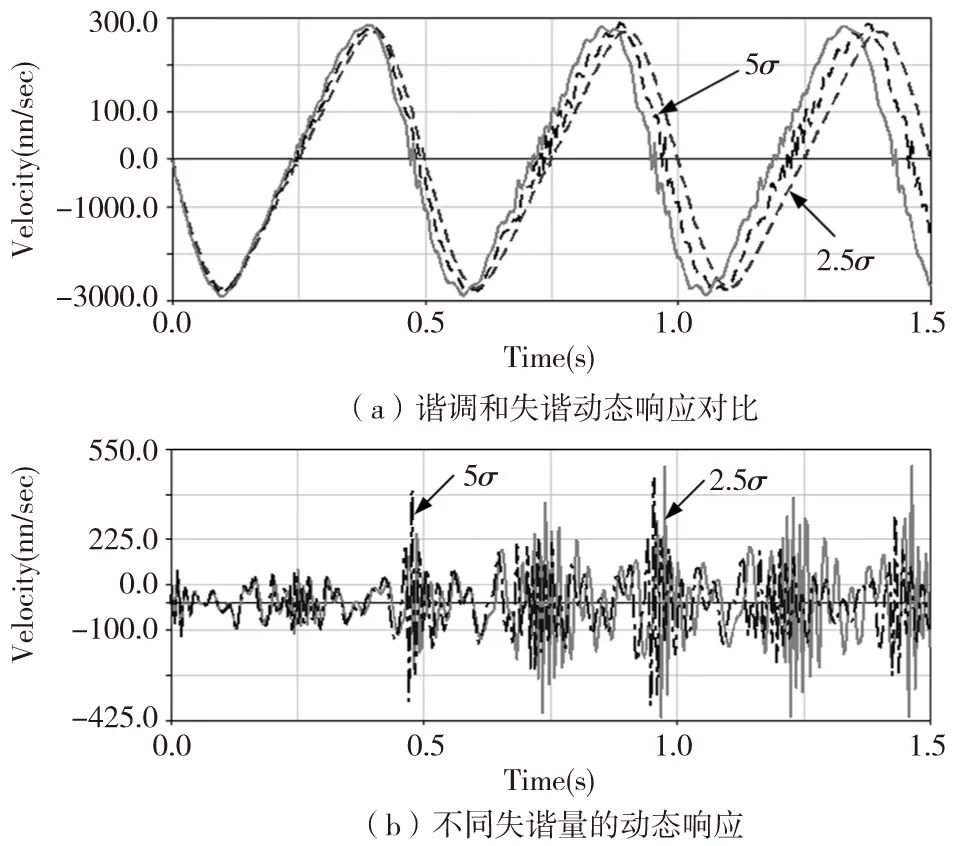
图5 动力失谐动态响应

在图5b中，速度的最大差值分别为445.94mm/s和490.45mm/s，但是较大的差值为动力失谐量为2.5σ的动态响应，并不是动力失谐量为5σ的动态响应。这种情况说明失谐动态响应与失谐量之间不是线性关系，机构失谐存在振动局部化现象，即在某些失谐量出现局部振动加剧现象，这与失谐振动在柔性机构内的传播有关，须在以后的研究中进一步深入探讨。

2.3 摩擦失谐的动态响应

摩擦力失谐动态响应为一个随机过程，即：在一个确定性仿真周期内，摩擦力的大小是随机的。摩擦力引起的滑块加速度失谐动态响应如图6所示，在图6a中，实线代表谐调动态响应，而虚线代表摩擦失谐动态响应。图6中，横坐标为时间，单位为s；纵坐标为加速度，单位为mm/s2。

图6 摩擦失谐动态响应

在图6b中，实线代表失谐量为5σ的加速度动态响应差，虚线代表失谐量为2.5σ的加速度动态响应差。5σ和2.5σ的加速度失谐动态响应相差不多，极值近似相等。说明摩擦失谐的灵敏度并不高，这种失谐差异主要不是由摩擦失谐导致的，而是由于柔性构件的“快变运动”即柔性机构的耦合振动导致的。

2.4 多因素失谐动态响应随机分析

失谐动态响应随机分析依靠传统的随机抽样分析(Monte Carlo)方法不可行，主要原因是计算成本过高。为了探索多因素失谐影响的柔性机构动态响应随机分布，提出了一种近似的分析方法以减少时间消耗。具体方法如下：假设考虑的失谐量区间为[-5σ，5σ]，均匀划分各个失谐量(假设失谐量的个数为p个)区间为若干个子区域(假设子区域的数量均为k个)，按照截尾正态分布在区间上随机抽样失谐量数据，并统计在子区域上出现抽样数据的频次；以子区域中心值作为该子区域的抽样数据(数据总量为kp)进行求解得到动态响应；统计动态响应数据及其对应的频次，即可得到动态响应的近似分布。

根据上述方法，只考虑质量和动力两种多因素失谐进行分析。以0、±σ～±5σ为子区域中心将质量和动力失谐量区间分别划分为11个子区域(共112=121个子区域组合)，将质量(均值为62.408，方差为1.019)和动力(均值为720，方差为3.464)按照正态分布抽样10000组数据并统计落入子区域组合的频次，这样，只计算121次失谐动态响应即可得到其分布特性。以滑块为研究对象，多因素失谐的滑块位移动态响应的最大差值统计分布如图7所示。在图7中，横坐标是位移失谐量动态响应差值，单位为mm，纵坐标是动态响应统计次数。

图7 多因素失谐动态响应分布特性

在图7中，位移动态响应分布为近似正态分布，均值为7.91，方差为1.1025。可见，能够产生失谐的因素是广泛存在的，周期机构尤其是柔性周期机构在运动过程中较易产生失谐动态响应。

3 结论

周期机构中的失谐现象在机构动态响应中普遍存在，应该像失谐结构一样引起足够的重视，积极探索失谐机构的分析理论和方法。

并联机构中失谐振动传播过程中会产生失谐动态响应，和失谐结构一样有振动局部化现象。

构件的失谐动态响应随机分布大致为正态分布，机构失谐动态响应对不同失谐因素的灵敏度各异。本文提出的多因素失谐随机分析方法简单实用，可以适用于其它多失谐因素的分析。

[1] Anderson P W. Absence of diffusion in certain random lattices[J]. Physics Review, 1958, 109: 1162-1660.

[2] Bendiksen O O. Mode localization phenomena in large space structure[J]. AIAA Journal, 1987,25(9):1241-1248.

[3] Bouzit D, Pierre C. An experimental investigation of vibration localization in disordered multi-span beams [J]. Journal of Sound and Vibration, 1995, 184(4):649-669.

[4] 刘济科，赵令诚. 结构振动模态局部化评述[J]. 振动与冲击，1995,14(4):1-4.

[5] 胡超，李凤鸣，邹经湘,等. 失谐叶片-轮盘结构振动局部化问题的研究[J]. 中国电机工程学报，2003,23(11):189-194.

[6] 于霖冲.谐调机构的失谐动态响应分析[J].机械传动，2015，39(1):31-34.

[7] 于霖冲，焦俊婷，李向宏. 基于RBF神经网络的柔性机构非线性运动模型辨识[J].组合机床与自动化加工技术，2005(11):29-30.

[8] 于霖冲，白广忱.柔性机构动态可靠性分析[M]. 北京：机械工业出版社，2012.

[9] Beck J B, Brown J M, Kaszynski A A, et al. Mistuned Response Prediction of Dual Flow-Path Integrally Bladed Rotors With Geometric Mistuning[J]. Journal of Engineering for Gas Turbines and Power,2015, 137(6):062501-1-9.

[10] Bai Bin, BAI Guangchen, LI Chao. Application of Improved Hybrid Interface Substructural Component Modal Synthesis Method in Vibration Characteristics of Mistuned Blisk[J]. Chinese Journal of Mechanical Engineering, 2014,27(6): 1219-1231.

(编辑 李秀敏)

Mistuned Dynamic Response Analysis Method of Parallel Flexible Mechanism

YU Lin-chong, LIN Zhi-shu, LIN Xing-yan

(School of Mechanical and Automotive Engineering，Xiamen University of Technology，Xiamen Fujian 361024,China)

The aim of the research is to study nonlinear dynamic responses of periodic mechanism in case of mistuned status. Especially for the highly nonlinear kinetic and dynamic parameters responses of flexible mechanism when mistuned. Based on Monte Carlo method, a basic method of mistuned dynamic responses analysis on flexible periodic mechanism were provided. A Parallel mechanism was taken as an example for dynamic response contrastive analysis in multiple mistuned case. Preliminary discussion on the variation rule of detuning and mistuned dynamic response was given. The results showed that mistuned dynamic responses were common in periodic mechanism. The relationship between detuning and dynamic response were nonlinear. Localization phenomenon of dynamic response was exist in periodic mechanism.

parallel mechanism；flexible mechanism；mistuned；dynamic response

1001-2265(2016)11-0050-03

10.13462/j.cnki.mmtamt.2016.11.014

2016-01-05；

2016-02-17

国家自然科学基金项目(51375412)

于霖冲(1968—)，男，长春人，厦门理工学院副教授，研究方向为系统可靠性、CAD及自动化、系统仿真，(E-mail)lcyu@xmut.edu.cn。

TH112；TG659

A