压力分布可控的高超声速进气道／前体一体化乘波设计

李怡庆，韩伟强，尤延铖，＊，潘成剑

1．厦门大学 航空航天学院，厦门 361005 2．北京空天技术研究所，北京 100074

压力分布可控的高超声速进气道／前体一体化乘波设计

李怡庆1，韩伟强1，尤延铖1，＊，潘成剑2

1．厦门大学 航空航天学院，厦门 361005 2．北京空天技术研究所，北京 100074

在二维弯曲激波高超声速进气道基础上，发展了一种压力可控的进气道／前体一体化乘波设计方法。通过事先指定前体／进气道壁面压力分布，结合二维特征线反设计方法，可以逆向设计出流向、横向压力分布规律都可控的进气道／前体外压缩段型面。采用该方法，设计了一种二维进气道／前体一体化方案，并对其进行数值模拟。结果表明：设计状态下，与不带侧板二维进气道相比，此类一体化方案中的进气道设计状态流量系数提高27%，出口压比提高48．5%，总压恢复系数提高10%；与楔导乘波理论设计的一体化方案相比，压力可控的一体化方案具有相似的外形尺寸和乘波特性，但进气道流量系数则较楔导乘波方案提高了5%，进气道出口压比提高6．4%，总压恢复系数提高2．3%。

高超声速；进气道／前体一体化；压力分布；乘波理论；二维高超声速进气道

近空间飞行器的设计和开发是当前国际航空航天领域的研究热点，也是各国竞相争夺空间技术的焦点之一［1－2］。自20世纪60年代以来，大量研究证明实现近空间飞行的关键在于推进系统与飞行器机体的一体化设计。1959年，Nonweiler首次提出适用于平面入射激波的高超声速飞行器设计方法，并将其命名为楔导乘波体（Caret Waverider）［3］。楔导乘波体是由平面斜激波后的流线生成，因为入射激波为平面斜激波，能够较好地与二维流动相耦合，所以早期被广泛运用于高超声速飞行器的一体化设计［4－5］。国际上，Ferguson基于楔导乘波理论完成了整个推进系统与飞行器机体的一体化设计［6］，该设计方法考虑了平面流动条件下的楔导乘波体与进气道耦合问题。20世纪90年代，Sobieczky等首次提出了根据给定激波形状生成乘波体的设计方法，并命名为吻切乘波理论（Osculating Cone Waverider）［7］。基于该方法，Takashima等进一步提出了能够实现外流乘波体与内流二维进气道良好耦合的一体化设计方法［8］。在国内，笔者团队进一步发展了乘波理论并将其与内收缩流动相结合，提出同时适用外流乘波体与内流三维内收缩进气道的双乘波一体化设计方案［9－10］，解决了高超声速外流与内流的匹配问题。贺旭照［11］、南向军［12］、范晓樯［13］和易军［14］等以进气道／前体一体化为研究对象，设计出了各类乘波进气道／前体一体化方案，并通过数值模拟与试验研究给出了进气道／前体一体化设计方案的气动特性。

国内外高超声速飞行器一体化方案多采用乘波理论设计。对于采用平面激波系的高超声速二元进气道，则多采用楔导乘波理论匹配前体设计［6］。该理论虽能在设计条件下为飞行器提供良好的升阻性能。然而，超声速状态的主流在进入进气道之前通常要经过相当一段前体外压缩，如何控制外压缩段的压力分布，减小主流的横向溢流及能量损失无疑是困难的。Lewis［15］提出了一种考虑横向压力梯度的乘波体外形修正方法，其基本思路是对设计好的乘波体方案进行改进，而不是从设计顶层开发一种压力可控的设计方法。因此，如何构造一种有效控制进气道外压缩段流向、横向压力分布的前体／进气道一体化方案仍然是亟待解决的关键问题。

通过事先指定前体／进气道壁面压力分布，结合二维特征线反设计方法，提出一种压力分布可控的高超声速前体／进气道一体化设计方法，并通过数值模拟证明了该方法的可行性。

1 一体化设计方法

压力分布可控的一体化设计方法的核心思想是逆向求解满足给定壁面压力分布的压缩面型线，主要手段是二维特征线方法（Two－dimensional Method of Characteristic，2D－MOC）［16－17］。传统的二维特征线法多为正向求解，以来流条件为初始参数，以压缩型线为边界条件，根据已知两点发出的异簇特征线，联立特征线方程和相容性方程求解特征线交点的参数，最终获得整个流场信息。而逆向二维特征线法的求解思路则与之相反，先给定来流参数和壁面沿程压力分布，再采用特征线法逆向求解压缩壁面型线的几何位置，将壁面压力分布等气动参数变成可设计的变量［18－19］。由于前体／进气道一体化方案是全三维的构型，对压力分布的控制又可以分为流向压力分布选取与横向压力梯度控制两部分。

1．1 流向压力分布选取

二维进气道压缩型面可以采用激波压缩或等熵压缩设计。等熵压缩设计可以最大程度地抑制进气道总压损失，但主要缺陷在于获得的压缩面通常较长。弯曲激波压缩则兼顾了激波压缩与等熵压缩的优点［20］。该压缩的特点为仅具有一道入射弯曲激波，激波之后的压缩型面将产生一系列等熵压缩波，弯曲激波与波后的等熵压缩波共同实现对高超声速来流的减速增压。基于上述优点，选取了如图1所示的二维曲面压缩基本流场。

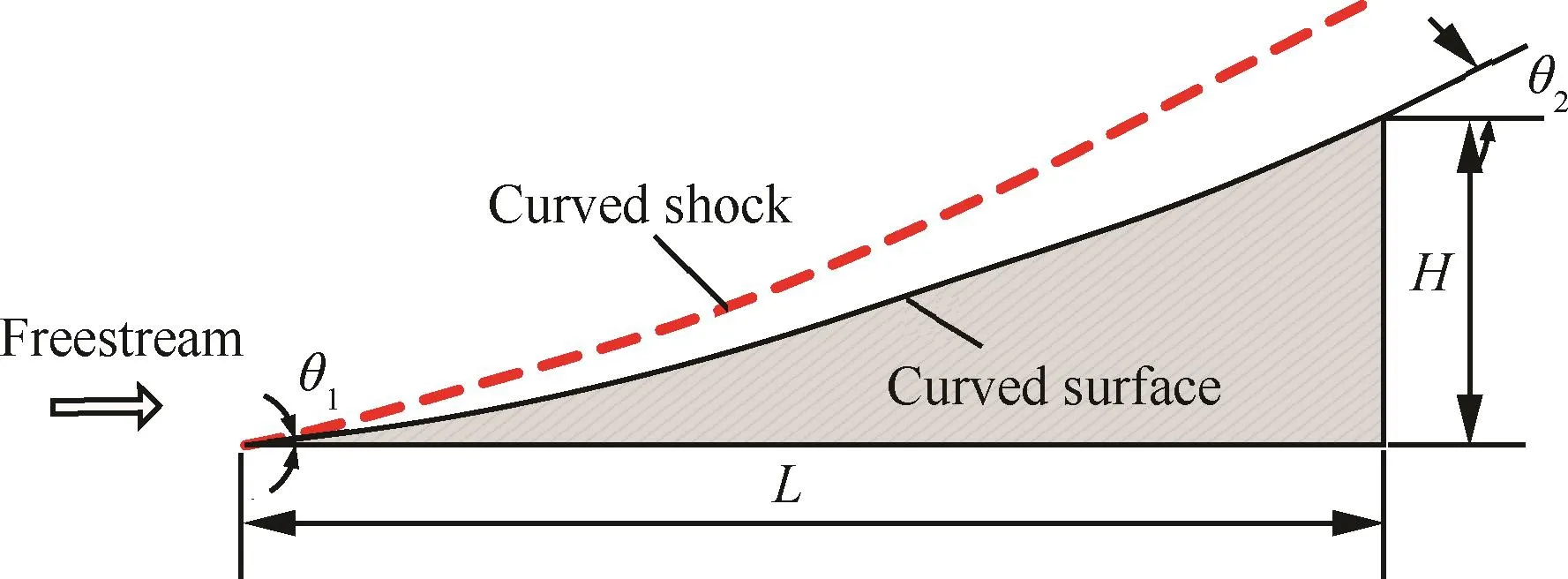
图1 二维曲面压缩基本流场结构Fig．1 Construction for 2Dcurved shock flowfield

该压缩型面长度为L，高度为H，初始转折角为θ1，终止转折角为θ2。压缩面曲线方程由以上4个参数控制，并运用3次方拟合生成。采用特征线方法，通过给定来流马赫数Main，来流静压p0，可以求解得到流场结构如图2所示，图中p为压力。前缘楔角产生的较弱斜激波，与弯曲壁面产生的等熵压缩波不断相交并相互叠加，使激波角度持续增大，最终形成弯曲激波。图2（a）给出了压缩面沿程壁面压力分布，激波后的压缩面为等熵压缩，故沿程压力保持规则的连续上升。图2（b）给出了二维曲面压缩流场的压比图。

图2 二维曲面压缩流场压比等值图Fig．2 Static pressure ratio contours of 2Dcurved shock flowfield

运用该曲面压缩二维基本流场，可构造混压式二维进气道，进气道由外压缩段和内压缩段组成。由于二维进气道存在一定宽度，若两侧无侧板限制，进气道将产生较大的横向压力差。该压力差会对进气道的二维流动特征产生影响，改变预设计的波系结构，导致该进气道在前体部分横向溢流，因此需要发展一体化方法实现对横向压力梯度的控制。

1．2 指定流向压力分布的二维逆特征线法

特征线法是一种求解双曲型偏微分方程的精确步进型方法。在定常超声速流场中，由于其控制方程为双曲型偏微分方程，流场中任一点的流动具有仅取决于上游流场中有限区域的性质，因此可以使用特征线法求解该流场。所谓特征线是指沿着该曲线积分将偏微分方程简化为易于求解的全微分相容性方程。在超声速流场中由于马赫线就是特征线，因此可将控制方程简化为以下两个全微分方程组：

特征线方程组为

相容性方程组为

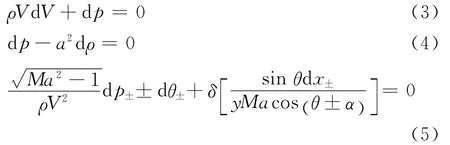
式中：λ为特征线斜率；v为沿y方向的速度分量；u为沿x方向的速度分量；θ为流动角；α为马赫角；ρ为密度；V为速度；a为声速；Ma为马赫数；δ为特征线系数用于区分流场类型，当δ为0时表征二维流场，当δ为1时表征轴对称流场；下标＋表示左行特征线，下标－表示右行特征线。

通过联立特征线方程组和相容性方程组求解特征线交点的参数，最终可获得获得整个流场信息。

而逆向二维特征线法的求解思路则与之相反，先给定来流参数和壁面压力分布，再采用特征线法逆向求解压缩壁面型线的几何位置，将壁面压力分布等气动参数变成可设计的变量。具体求解过程如图3所示。在给定来流参数和壁面压力分布的条件下，可以在前缘激波的起点位置定义出一块很小的均匀流场区域ABC。此时，若以右行特征线BC为特征线边界条件Γ0，配合边值条件即壁面压力分布Γ1（x），可以采用特征线法逆向求解壁面型线及下游流场。

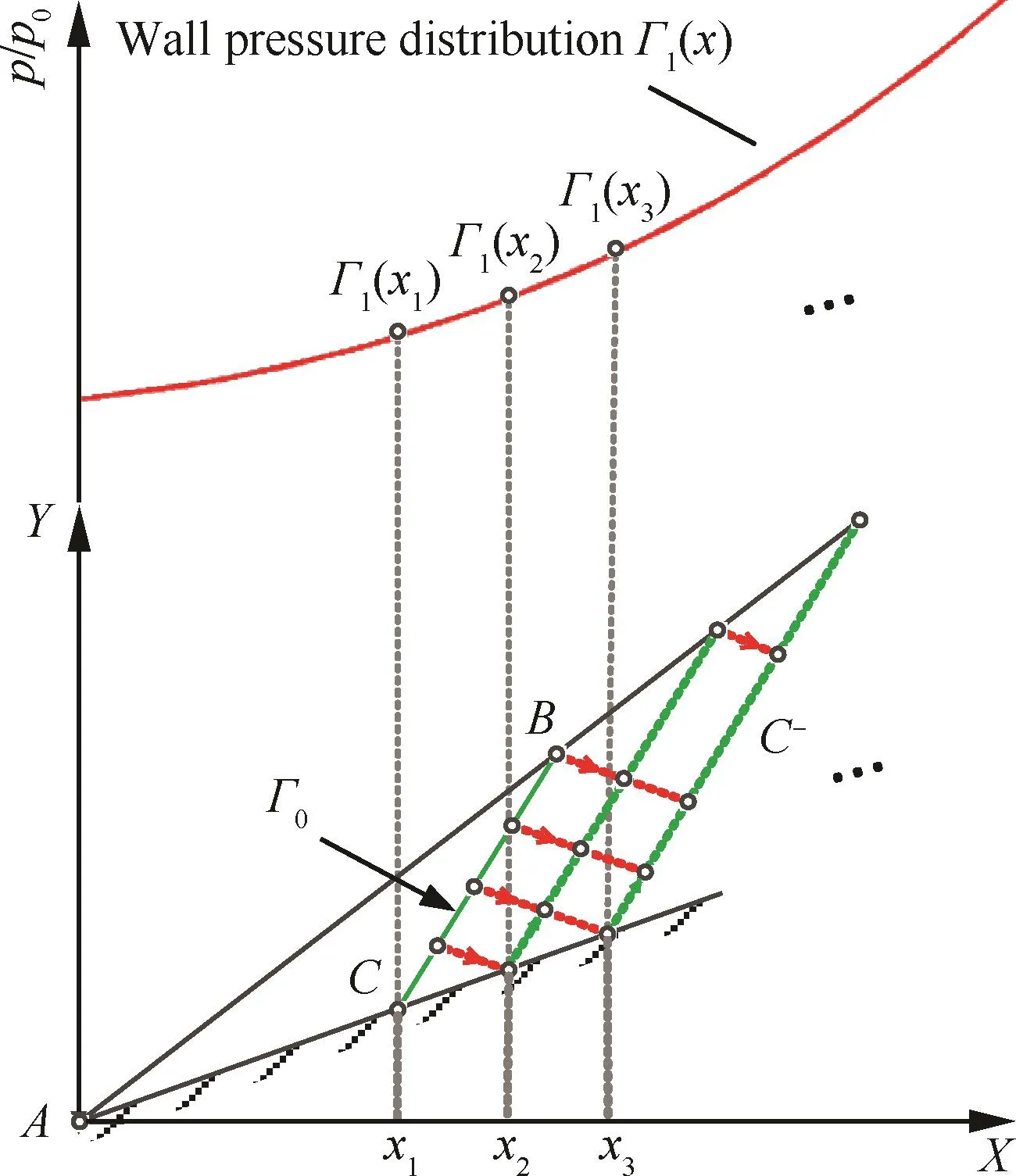
图3 逆向二维特征线法示意图Fig．3 Schematic of inverse 2Dmethod of characteristic

需要特别指出，根据给定流向压力梯度反求壁面型线的过程是实现横向压力分布控制的关键，对于二维弯曲激波来说，计算指定压力分布的壁面型线，只能通过逆向特征线法获得。该设计方法明显有别于楔导乘波体的设计。以图2为例，在自由来流情况下，满足a′b′段压力分布的壁面型线如图4中a′b1′所示。然而，楔导乘波体的设计方法在相同位置内的壁面型线为图2中的流线，即图4中的虚线a′b2′。显然，a′b1′将构造出与a′b2′截然不同的壁面压力分布规律，使得提出的一体化设计方法不同于传统的楔导乘波体设计方法，在对比分析中也会进一步说明。

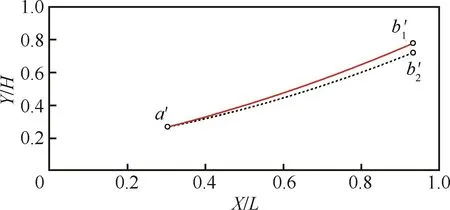
图4 2种方法壁面型线几何形状对比Fig．4 Wall profiles corresponding to two types of methods

1．3 横向压力梯度控制

为了实现对横向压力的控制，下面结合图5对高超声速进气道／前体一体化设计方法进行阐述。

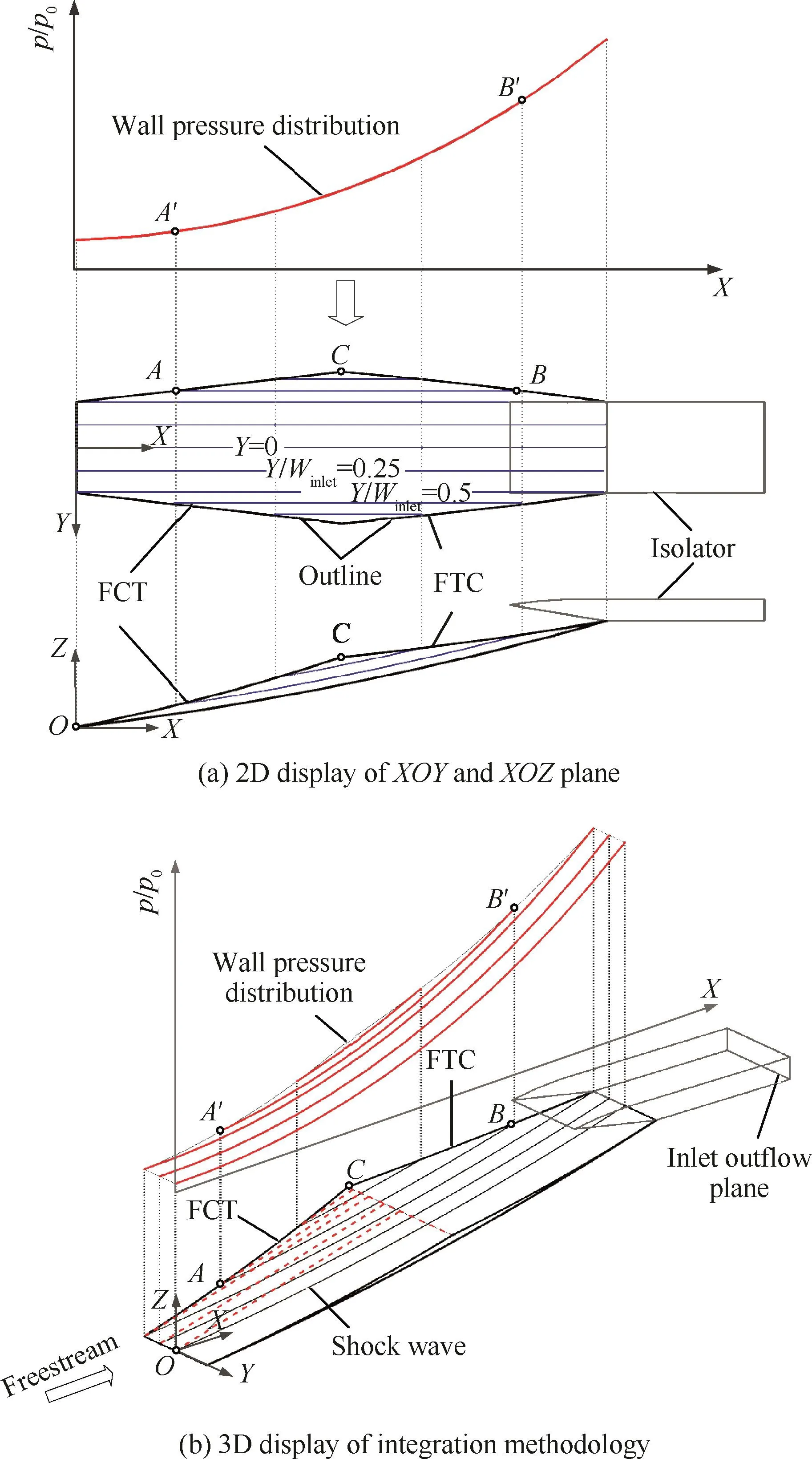
图5 横向压力梯度控制设计原理图Fig．5 Schematic of horizontal pressure gradient control concept

1）指定一体化方案XOY平面外轮廓曲线。

一体化方案外轮廓由图5中A点所在前缘捕获型线（Flow Capture Tube，FCT）与B点所在前体终止线（Forebody Terminating Curve，FTC）两部分组成。其中，前缘捕获型线包括进气道前缘型线与前体前缘型线，选取的进气道前缘型线为平直段，前体前缘型线为3次曲线，如式（6）所示，控制参数为前缘起点坐标（x0，y0），起点斜率为dy0，终点坐标为（x1，y1），终点斜率为dy1。前体终止线为前体最大宽度点C与进气道边缘肩点的连线：

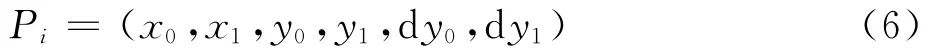
2）指定前缘捕获型线XOZ平面投影。

前缘捕获型线在XOZ平面内的投影形状指定为与基准流场的弯曲激波形状相同，如图5（a）所示。前缘线外轮廓的XOZ平面投影形状与弯曲激波相同有利于一体化方案形成附着于压缩型面的入射激波面，使前体横向压力分布可控的同时兼具乘波的特点。

3）根据预先指定的压力分布，将前缘线离散，反求每一个XOZ平面内的壁面型线分布。

以前体前缘点A为例，过前缘点A生成流向XOZ平面，该平面与前体外轮廓线相交于点B。根据A、B两点的流向位置可在图2给定的流向压力中提取需要的壁面压力分布，如图5中A′B′所示。然后，运用基于壁面压力分布的二维特征线法反求得XOZ平面内的壁面型线AB，并在每一个XOZ平面内以相同步骤求取对应壁面型线。

4）组合离散的壁面型线生成三维前体。

根据步骤3）获得的XOZ平面离散型线依据前缘位置依次进行叠加，可以得到前体的三维形状。将三维形状截止于终止点处，即可获得一体化方案的前体表面。

5）与进气道相耦合，并将前缘捕获型线沿流向拉伸，获得一体化方案下表面。

前体压缩型面最靠近进气道压缩面的壁面型线与进气道具有相同的壁面压力分布，所以，必然与进气道压缩型线具有相同的形状。两部分自然实现连续过渡，由此完成横向压力可控的高超声速进气道／前体一体化设计。

从本质上说，提出的一体化乘波设计方法，在流向和横向2个维度对进气道／前体的压力分布进行了细致的流动控制。通过给定2个维度的压力分布并逆向求解固壁形状的方法，获得了全三维的进气道／前体一体化设计方案。该方案的最大优点在于横纵向压力梯度都是可控的，因此可以有效地避免不必要的横向溢流，从而用尽可能小的前体宽度实现高的进气道流量捕获系数。而在相同来流和进气道压缩的情况下，高的流量捕获系数必然带来较高的出口总压恢复系数，这将全面提高进气道／前体一体化方案的总体性能。

1．4 一体化设计方法应用实例

图6为采用上述一体化设计方法得到的前体／进气道。设计飞行高度为27km，来流马赫数Main＝6．5，来流静压p0＝1 880Pa。根据前体宽度约束，总宽度W＝0．4m，进气道宽度Winlet＝0．24m。一体化方案总长度L＝2m，外压缩段长度Lext＝1．14m。进气道捕获面积Acapture＝0．077m2，总收缩比CR＝5．3。

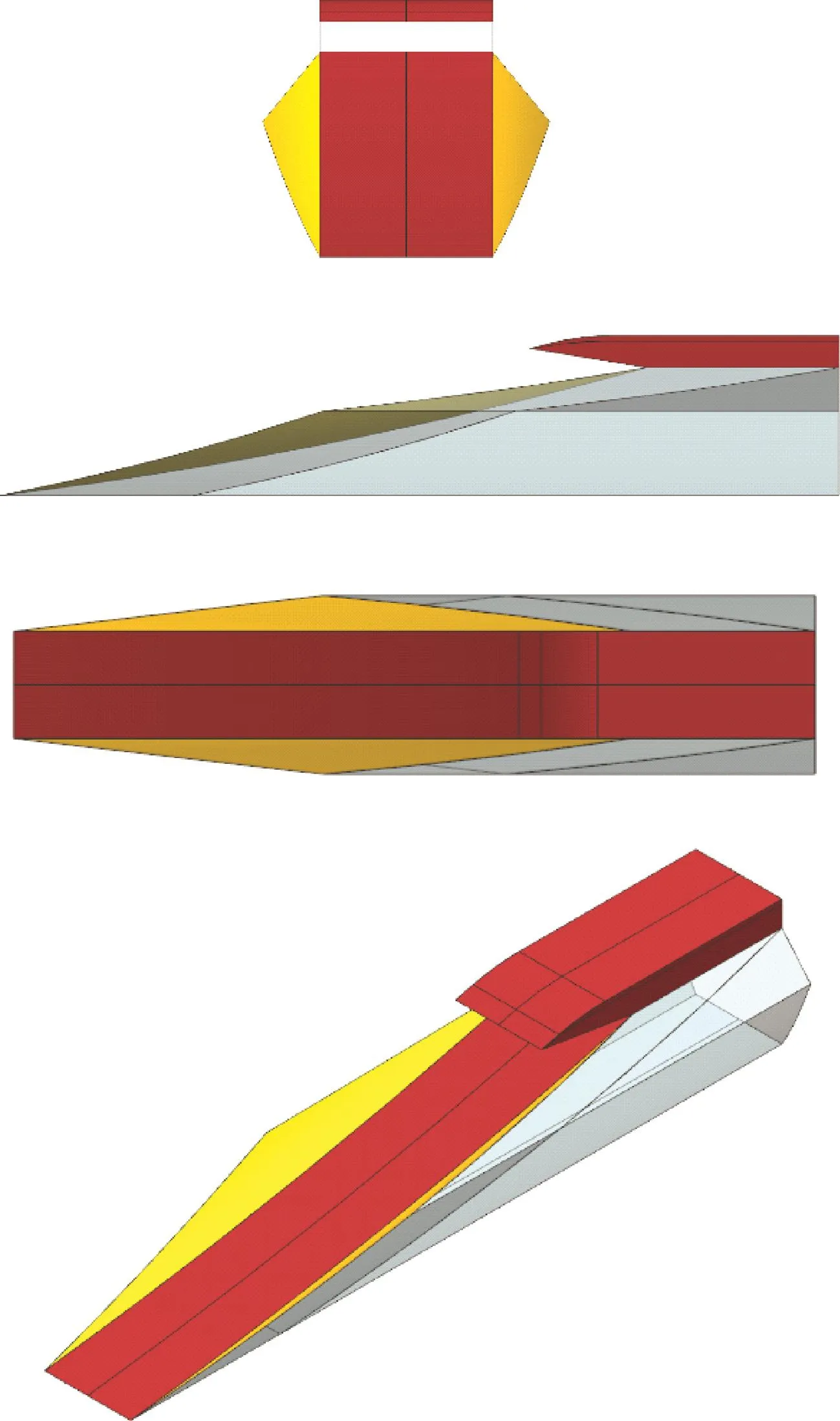
图6 进气道／前体一体化方案三维视图Fig．6 3Dview of inlet and forebody integration configuration

2 进气道／前体一体化方案流动特征分析

对进气道／前体一体化方案在设计与非设计状态下分别进行了无黏及有黏的数值模拟。无黏通量采用2阶Upwind的Roe－FDS格式，湍流模型采用SSTk－ω两方程模型。考虑到气体的高温效应，计算中采用考虑变比热的热完全气体模型。在无侧滑角情况下流动具有对称性，因此仅对1／2流场进行网格划分，网格总数约为300万。分子黏性系数采用Sutherland公式计算，对壁面取绝热无滑移和固体边界条件，进出口采用压力远场和压力出口边界条件。当各残差指标下降至少3个数量级，且进出口流量守恒时判定收敛。

图7（a）为二维计算流体力学（CFD）计算获得的单纯进气道压比等值图，该二维进气道在无黏设计状态下隔离段出口马赫数Maout＝3．6，增压比pout／p0＝17．23，总压恢复系数pout＊／p0＊ ＝0．57。图7（b）为进气道／前体一体化方案三维计算获得的对称面上无黏压比等值图。可以看出，设计的一体化方案对称面压比分布规律与二维CFD计算获得的进气道压比基本一致，保持了原进气道中的波系特点。这证明了压力可控的进气道／前体一体化方案并不会因为侧向溢流而影响主要流动特征，在对称面处能够完全复现二维CFD计算结果。

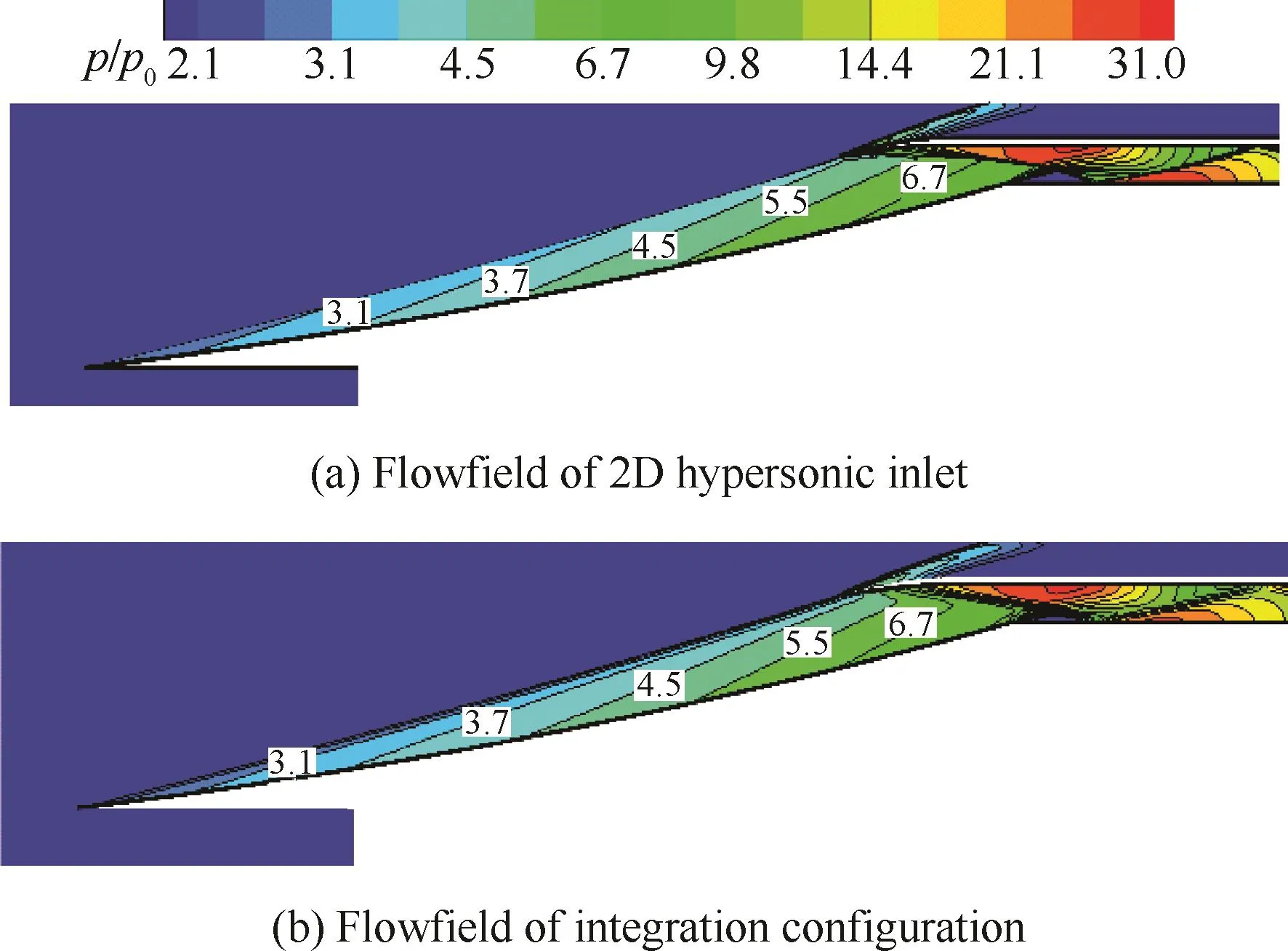
图7 对称面压比等值对比图Fig．7 Inviscid pressure ratio contours comparison in symmetry plane

图8为图5（a）中所示一体化方案的3个流向特征切面（Y ＝0，Y／Winlet＝0．25，Y／Winlet＝0．5）处壁面压力分布与目标壁面压力分布对比。在3个不同的特征切面内，除了起始点附近外，进气道外压缩段的压力分布与目标压力分布均吻合良好。因此，在进气道壁面外压缩段几乎不存在压力差，这符合控制横向压力梯度的设计思想。

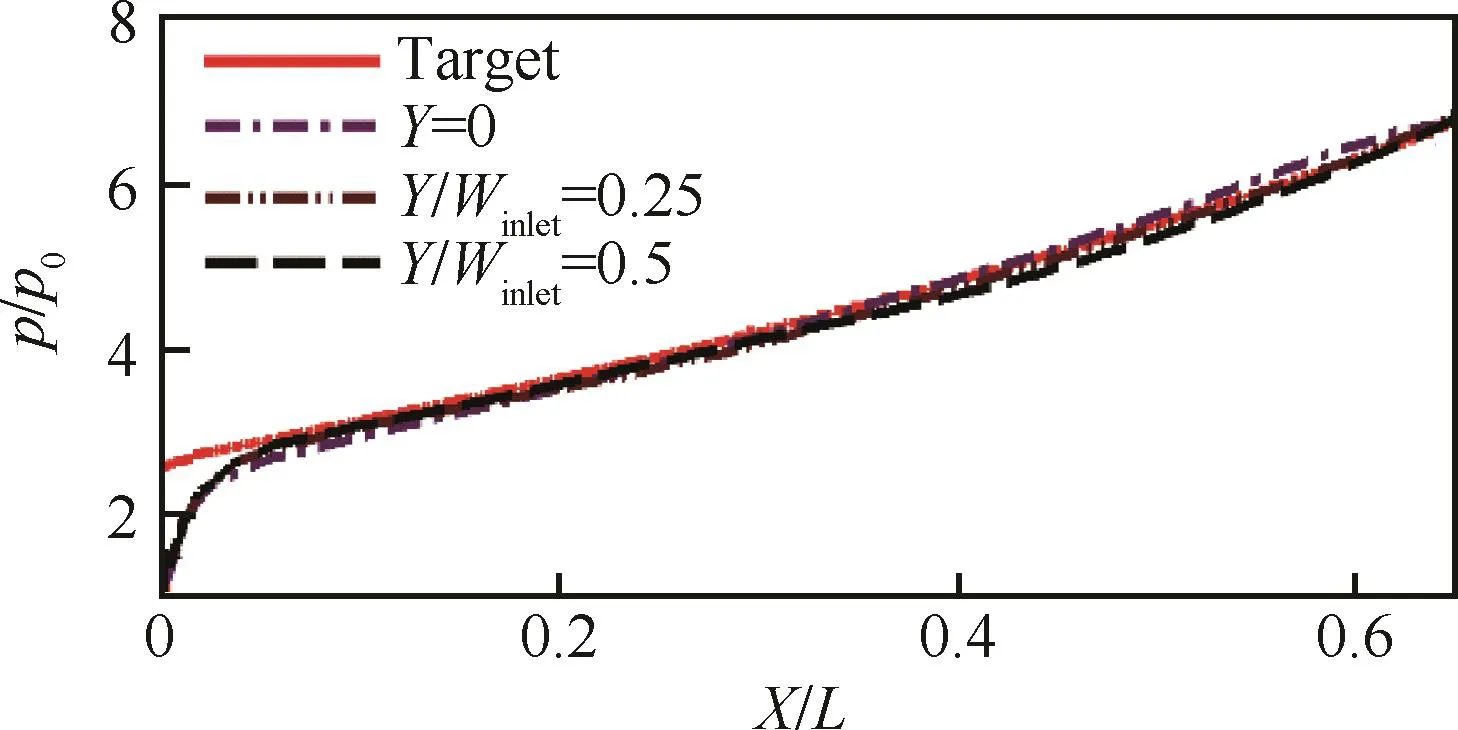
图8 进气道外压缩面沿流向切面压力分布规律Fig．8 Pressure distribution in external compression surface along flow direction

3 进气道／前体一体化方案性能对比

3．1 三维外形与截面流动特征对比

为了对比说明设计的一体化方案的主要特点，设计了单独二维进气道不带侧板的方案，如图9（a）所示，以及使用楔导乘波体方法的前体（Caret Waverider Forebody，CWF），一体化方案如图9（b）所示。从图9中可以看出，提出的压力可控的一体化（Preassigned Pressure Forebody，PPF）方案，如图9（c）所示，实际上与楔导乘波体方案具有十分相似的外形尺寸和乘波特性。但是如果对其横截面的流动特征进行仔细对比分析，会发现3种方案间还是存在着明显不同。

图9 不同截面沿程无黏流场结构Fig．9 Inviscid flowfield with several sections along flow direction

图9（a）为不带两侧前体时的单纯二维进气道流场。从图9中看，此时进气道外压段存在极大的横向压力差，入射激波明显向两侧下弯曲。这主要因为高超声速来流经过入射激波压缩，压力升高，但进气道两侧仍为来流静压，由此产生了明显的横向压力梯度和溢流，进气道性能将显著下降。对比两种一体化方案，见图9（b）和图9（c），二者的入射激波都保持为平面激波，且完全贴合于飞行器前体最大宽度之前的表面，因此在飞行器前端基本无横向溢流。当气流抵达进气道进口截面，楔导乘波一体化方案（图9（b））在进气道捕获截面的两侧，压力等值线存在向两侧下降的趋势，这仍将导致横向的压力梯度以及部分溢流。而在相同截面位置处，压力可控的一体化方案（图9（c））的横截面压力等值线分布十分均匀，且基本都保持与Y轴平行，由此保证了在整个截面内基本没有横向压力梯度，不会引起额外的横向流动。

通过引入二维特征线反设计方法，进气道／前体外压缩段横向压力分布规律变得可以控制，这为进气道／前体的一体化设计增加了一个可控自由度，也将有效减弱进气道的横向溢流。

3．2 壁面压力分布对比

楔导乘波一体化方案与设计的压力可控的一体化方案外压缩面的壁面压力分布等值图如图10所示。图10上半部分为楔导乘波一体化方案外压缩面压力等值图。因两侧乘波前体的作用，进气道外压段横向压力分布较为均衡，但在d截面位置以后，因两侧前体尺寸的迅速减小，压力分布明显的中间高两侧低，且越靠近进气道入口该趋势越严重。

图10下半部分为压力可控的一体化方案外压缩面压力分布等值图。从图中可看出由于前体的横向压力控制作用，前半段与楔导乘波一体化方案规律类似，保持了进气道横侧向压力梯度小的优点。在外压段的后半段（d截面以后），压力可控方案能够提供两侧相对较高的压力趋势。该效果使得后半段横向压力分布略微呈现两侧高中间低的趋势，且该趋势一直保持到进气道入口。

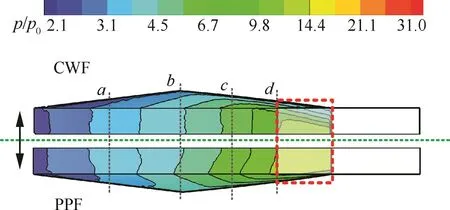
图10 一体化方案外压缩面的壁面压力分布等值图Fig．10 Static pressure contours along compression wall of integration configurations

图11为图10所示的沿程各截面壁面横向压力对比图。图中虚线表示楔导乘波一体化方案的壁面压力分布，而实线表示压力可控的一体化方案的壁面压力分布。对比虚线与实线的走势可以得出，在具有乘波特性的a、b截面内，二者具有类似的分布规律，即进气道中部与两侧的压力基本相等。但沿流向发展至c、d截面处时，压力可控一体化方案所具有的优势逐步显现。该优势表现为进气道两侧压力仍能与进气道中部相匹配，而楔导乘波一体化方案两侧压力明显下降，该分布将导致进气道产生不希望的横向溢流。

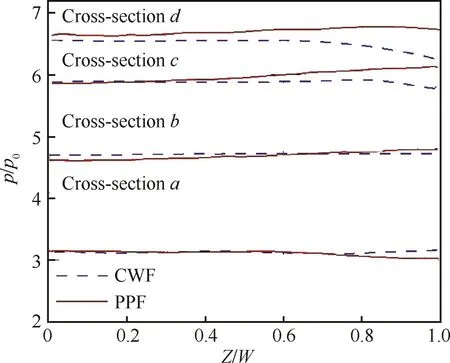
图11 沿程各截面壁面横向压力对比Fig．11 Variation of static pressure distribution along wall with several cross－sections

3．3 出口流场特性对比

图12为全三维CFD计算获得的单纯进气道隔离段出口及进气道／前体一体化方案进气道隔离段出口总压分布图谱，图中σ为总压恢复系数。可以看到两方案出口低能流均分布于出口截面角区以及壁面区域。然而两方案却有显著的不同，图12（a）为单纯进气道隔离段出口，因两侧压力衰减导致横向压力畸变增加。此外，受到分离区影响，隔离段出口下壁面靠近对称面区域出现较为明显的低能区，高总压区分布于界面中央偏上壁面位置。

图12（b）为进气道／前体一体化方案进气道隔离段出口总压恢复分布图。一体化前体对进气道横向压力变化起到了很好的抑制作用，低能区不再向中心汇聚而是均匀地分布于壁面区域。这将有利于隔离段出口均匀性的提高。另一方面，CFD计算结果显示，图12（b）中进气道／前体一体化方案出口总压恢复系数相对于单纯二维进气道提高了10%，进气道的出口均匀性得到了有效改善。

图12 进气道出口总压分布Fig．12 Total pressure distribution of inlet outflow

3．4 性能参数对比

表1给出了不同方案间的性能参数对比，这里指的都是进气道隔离段出口的性能参数，表中m为流量系数。在设计来流马赫数（Main＝6．5）下，压力可控的一体化方案的流量捕获系数最高，和不带侧板的二维进气道相比，流量系数提高了27%，和楔导乘波一体化方案相比，流量系数提高了5%；进气道出口压比方面，和不带侧板的二维进气道相比，出口压比提高了48．5%，和楔导乘波一体化方案相比，出口压比提高了6．4%；总压恢复系数方面，压力可控的一体化方案也具有最好的性能，和不带侧板的二维进气道相比，总压恢复提高了10%，和楔导乘波一体化方案相比，总压恢复提高了2．3%。总体而言，对于一样的二维进气道外形，因为引入了压力分布可控的一体化设计概念，飞行器进气道／前体的横向压力梯度得到有效抑制，进气道原本存在的横向溢流被基本消除，由此带来的收益不仅仅体现在流量系数上，而且放映在进气道的总体性能，包括进气道出口压比和总压恢复系数都得到了改善。

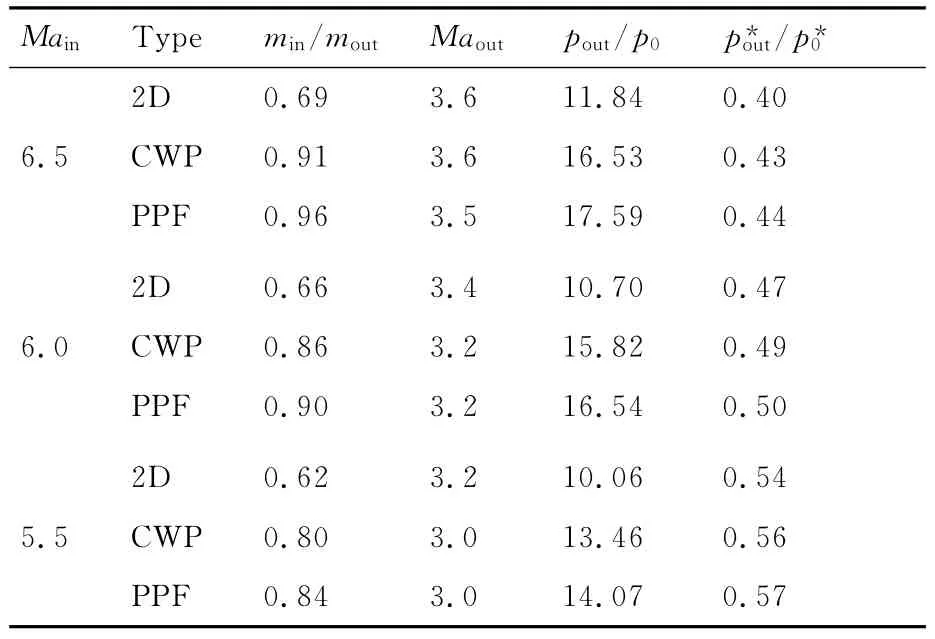
表1 不同方案间性能参数对比Table 1 Performance parameters comparison of different integration methodologies

对于非设计状态，分别评估了马赫数6、飞行高度26km，以及马赫数5．5、飞行高度23km 2个状态。从表1中可以看出，压力可控的一体化方案隔离段出口总压恢复系数随马赫数的降低而升高，马赫数为6时总压恢复系数为0．5，马赫数为5．5时总压恢复系数达到0．57。在不同非设计状态下，压力可控的一体化方案无论是在流量系数、出口压比还是总压恢复系数等各方面的参数都较楔导乘波一体化方案有所提高，其中，流量系数的涨幅在4%以上。若与不带侧板的二维进气道相比，流量系数上升更加明显，普遍达到20%以上。

3．5 进气道阻力特性对比

对不带侧板的二维进气道与压力可控的一体化方案内壁面上的阻力特性对比分析，为使两方案更具可比性，两方案各阻力变化均为无因次化后的阻力系数，两方案内壁面上的压差阻力系数CDP、摩擦阻力系数Cf及内壁面阻力系数CD在不同来流马赫数Main条件下的参数如表2所示。

由表2可知，两方案具有较为相似的阻力特性。随着马赫数增加来流静压大幅的降低，因此内壁面上的压差阻力系数CDP随着马赫数的减小而增大。然而，马赫数的提高增强了进气道内的激波强度，使激波与附面层之间的相互作用增强，导致摩擦阻力系数Cf随着马赫数的减小而减小。对比两方案的阻力系数值，压力可控的一体化方案因添加了两侧前体（表面积增加30%），因此表2中压差阻力系数CDP和摩擦阻力系数Cf相对于不带侧板的二维进气道分别略微有所增加（21%和13%）。综合表1和表2来看，提出的一体化方案较二维方案，以20%的阻力代价换取了10%的总压恢复提升和48．5%的压比上升。

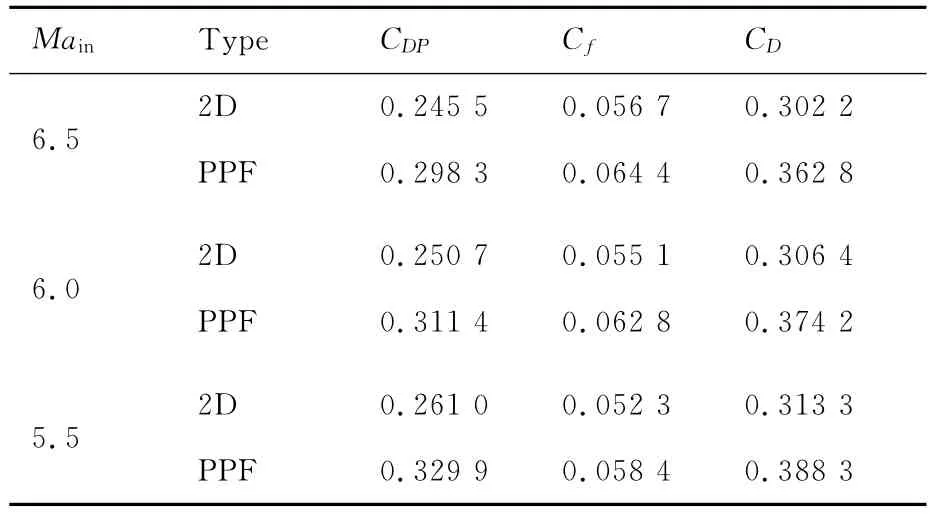
表2 不同方案间阻力系数对比Table 2 Drag coefficients compansion of different integration methodologies

4 结 论

1）压力分布可控的高超声速前体／进气道一体化设计方法能够复现原二维进气道的壁面压力分布，且在进气道的任意流向截面内的壁面压力分布与事先指定壁面压力分布均吻合良好，能够构造出二维进气道所需的流动特征。

2）压力可控的高超声速前体／进气道一体化设计方法在前缘捕获型线与外压缩段横向压力分布之间引入了二维特征线反设计法，因此可根据不同的壁面沿程压力分布进行设计，这为前体／进气道一体化设计增加了设计裕度。

3）虽然压力分布可控的一体化方案与楔导乘波一体化方案具有非常相似的三维外形，但数值模拟结果显示，压力可控的一体化方案能够有效提高进气道性能。设计状态下，该方案的进气道流量系数较楔导乘波方案提高了5%，出口压比提高6．4%，总压恢复系数提高2．3%。

4）压力分布可控的高超声速进气道／前体一体化方案两侧前体表面积相对无侧板二维进气道增加30%，但内壁阻力系数在设计状态下仅增加20%。以20%的阻力代价能够为进气道提供10%的总压恢复提升和48．5%的压比提升。

［1］ KURANOV A， KORABELNIKOV A． Atmospheric cruise flight challenges for hypersonic vehicles under the ajax concept［J］．Journal of Propulsion ＆ Power，2012，24（6）：1229－1247．

［2］ 尤延铖，梁德旺，郭荣伟，等．高超声速三维内收缩式进气道／乘波前体一体化设计研究评述［J］．力学进展，2009，39（5）：513－525．YOU Y C，LIANG D W，GUO R W，et al．Overview of the integration of three－dimensional inward turning hypersonic inlet and waverider forbody［J］．Advances in Mechanics，2009，39（5）：513－525（in Chinese）．

［3］ NONWEILER T R F．Aerodynamic problems of manned space vehicle［J］．Journal of the Royal Aeronautical Society，1959，6（3）：34－40．

［4］ FRANCOIS F，LAURENT S．The French LEA flight test program－status in 2008：AIAA－2008－2541［R］．Reston：AIAA，2008．

［5］ LEWIS M．A hypersonic propulsion airframe integration overview：AIAA－2003－4405［R］．Reston：AIAA，2003．

［6］ FERGUSON F．Adesign concept for the construction of a complete hypersonic vehicle from 2Dflowfields：AIAA－2005－3363［R］．Reston：AIAA，2005．

［7］ SOBIECZKY H，DOUGHERTY F C，JONES K．Hypersonic waverider design from given shock waves［C］／International Hypersonic Waverider Symposium．Washington D．C．：University of Maryland，1990．

［8］ TAKASHIMA N，LEWIS M，LOCKWOOD M，et al．Waverider configuration development for the dual fuel vehicle［C］／International Space Planes and Hypersonic Systems and Technologies Conference．Reston： AIAA，1996：1－12．

［9］ YOU Y．Dual waverider concept for the integration of hypersonic inward－turning inlet and airframe forebody［C］／International Space Planes and Hypersonic Systems and Technologies Conference．Reston：AIAA，2009：1－10．

［10］ LI Y，YOU Y．Integration methodology for waverider－derived hypersonic inlet and vehicle forebody［C］／19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference．Reston：AIAA，2014：1－13．

［11］ 贺旭照，秦思，周正，等．一种乘波前体进气道的一体化设计及 性 能 分 析 ［J］．航 空 动力学报，2013，28（6）：1270－1276．HE X Z，QIN S，ZHOU Z，et al．Integrated design and performance analysis of waverider forebody and inlet［J］．Journal of Aerospace Power，2013，28（6）：1270－1276（in Chinese）．

［12］ 南向军，张堃元，金志光．乘波前体两侧高超声速内收缩进气道一体化设计［J］．航空学报，2012，33（8）：1417－1426．NAN X J，ZHANG K Y，JIN Z G．Integrated design of waverider forebody and dateral hypersonic inward turning inlets［J］．Acta Aeronautica et Astronautica Sinica，2012，33（8）：1417－1426（in Chinese）．

［13］ 范晓樯，李桦，易仕和，等．侧压式进气道与飞行器机体气动一体化设计及实验［J］．推进技术，2004，25（6）：499－502．FAN X Q，LI H，YI S H，et al．Experiment of aerodynamic performance for hypersonic vehicle integrated with sidewall compression inlet［J］．Journal of Propulsion Technology，2004，25（6）：499－502（in Chinese）．

［14］ 易军，肖洪，商旭升．两种高超声速一体化构型的气动性能对比分析［J］．航空工程进展，2011，2（3）：305－311．YI J，XIAO H，SHANG X S．Aerodynamic performance research of two integrated hypersonic configurations［J］．Advances in Aeronautical Science and Engineering，2011，2（3）：305－311（in Chinese）．

［15］ LEWIS M．Aerodynamics for optimal engine－integrated airbreathing launcher configurations： AIAA－2004－3983［R］．Reston：AIAA，2004．

［16］ ZUCROW M J，HOFFMAN J D．Gas dynamics［M］．New York：John Wiley ＆Sons，Inc．，1976：463－497．

［17］ ANDERSON B H．Design of supersonic inlets by a computer program incorporating the method of characteristics：NASA TN D－4960［R］．Washington，D．C．：NASA，1969．

［18］ 南向军，张堃元，金志光，等．压升规律可控的高超声速内收缩进气道设计［J］．航空动力学报，2011，26（3）：518－523．NAN X J，ZHANG K Y，JIN Z G，et al．Investigation on hypersonic inward turning inlets with controlled pressure gradient［J］．Journal of Aerospace Power，2011，26（3）：518－523（in Chinese）．

［19］ 郭善广，王振国，赵玉新，等．高超声速二元进气道前体曲线 激 波 逆 向 设 计 ［J］．航 空 学 报，2014，35（5）：1246－1256．GUO S G，WANG Z G，ZHAO Y X，et al．Inverse design of the Fore－body curved shock wave of the hypersonic planar inlet［J］．Acta Aeronautica et Astronautica Sinica，2014，35（5）：1246－1256（in Chinese）．

［20］ 潘瑾，张堃元，金志光．弯曲激波压缩型面的设计及数值分析［J］．推进技术，2008，29（4）：438－442．PAN J，ZHANG K Y，JIN Z G．Design and numerical investigation of curved shock compression surface［J］．Journal of Propulsion Technology，2008，29（4）：438－442（in Chinese）．

Integration waverider design of hypersonic inlet and forebody with preassigned pressure distribution

LI Yiqing1，HAN Weiqiang1，YOU Yancheng1，＊，PAN Chengjian2
1．School of Aeronautics and Astronautics，Xiamen University，Xiamen 361005，China 2．Beijing Aerospace Technology Institute，Beijing 100074，China

On the basis of two－dimensional curved shock hypersonic inlets，a new integration，waverider design，of hypersonic inlet and forebody with preassigned pressure distribution is presented．A proper streamwise pressure distribution is assigned as the first step according to the shape of a curved shock wave．Afterwards，the external compression part of the inlet and forebody with controllable wall pressure distribution could be designed using the inverse two－dimensional method of characteristics．An integrated configuration is then derived from this concept and numerically studied．The results show that，on the design point，the flow capture ratio of the integrated configuration is enhanced by 27%compared with the pure two－dimensional inlet without sidewalls．The pressure ratio coefficient of inlet outflow rises by 48．5%，and the total pressure recovery coefficient is 10%higher than the no－sidewall inlet．In addition，compared with the Caret integration case，although with the same geometry shape and waverider character，the performance of mass flow rate，pressure ratio and total pressure recovery coefficient are 5%，6．4%，and 2．3%improved，respectively．

hypersonic；inlet and forebody integration；pressure distribution；waverider concept；two－dimensional hypersonic inlet

2015－09－09；Revised：2015－10－25；Accepted：2016－01－12；Published online：2016－02－23 08：59

URL：www．cnki．net／kcms／detail／11．1929．V．20160223．0859．002．html

s：National Natural Science Foundation of China（91441128，51276151）；National Defense Basic Scientific Research（B1420133058）

V231．3

A

1000－6893（2016）09－2711－10

10．7527／S1000－6893．2016．0017

2015－09－09；退修日期：2015－10－25；录用日期：2016－01－12；网络出版时间：2016－02－23 08：59

www．cnki．net／kcms／detail／11．1929．V．20160223．0859．002．html

国家自然科学基金（91441128，51276151）；国防基础科研项目（B1420133058）

＊通讯作者．Tel．：0592－2186849 E－mail：yancheng．you＠xmu．edu．cn

李怡庆，韩伟强，尤延铖，等．压力分布可控的高超声速进气道／前体一体化乘波设计［J］．航空学报，2016，37（9）：2711－2720．LI Y Q，HAN W Q，YOU Y C，et al．Integration waverider design of hypersonic inlet and forebody with preassigned pressure distribution［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：27112－720．

李怡庆 男，博士研究生。主要研究方向：高超声速进气系统设计。

Tel．：0592－2186849 E－mail：yiqingxmu＠163．com尤延铖 男，博士。主要研究方向：航空宇航推进理论与工程。Tel．：0592－2186849

E－mail：yancheng．you＠xmu．edu．cn

＊Corresponding author．Tel．：0592－2186849 E－mail：yancheng．you＠xmu．edu．cn