在小学高年级数学教学中强化方程思想的教学新探
邹国星
多年的教学实践发现,方程思想的渗透在小学高年级是一个棘手的问题。本文将结合具体的教学实践,探讨强化学生方程思想的教学方法及策略,为中小衔接打好基础,提升学生的数学素养。
一、数学教学中强化方程思想遇到的障碍分析
方程思想,是指从问题的数量关系入手,运用数学语言将问题中的条件转化为数学模型,然后通过解方程(组)或不等式(组)来使问题获得解决。方程思想的核心体现就是建模思想与化归思想。
1.渗透建模思想存在的障碍
(1)强势的算术思维定势
所谓的定势,是指由于心理操作活动的积累而形成的解决问题的刻板和准备状态,是人们在过去经验的影响下,解决问题的倾向性。学生从一年级到四年级,所接触的、学习的都是基于现实数字的操作。经过四年的数学训练,学生已经习惯于用算术法解决问题,“通过运算得到结果”这一心理操作过程在学生头脑中已根深蒂固。
(2)解题步骤繁杂,学生心理排斥
算术法是用算式来表示思维的过程,从形式上来看相对简洁。而列方程解应用题有其严格、规范的步骤与格式,特别是要写出一长串的文字,以说明将哪个未知数假设成已知数,学生感觉书写上特别烦琐,从而排斥用方程法解决问题。
(3)列方程存在方法上的缺陷
由于学生长期用算术法解决问题,而用方程法时未知数要参与列式、运算,这对于有些学生来说是一个比较难理解的过程,所以有些学生不是不喜欢“方程”,而是不会运用,只能“敬而远之”。具体表现在以下几方面:不会找等量关系式、不会假设合适的未知量、不会解方程。
2.渗透化归思想存在的障碍
(1)学生方面的原因
①已有经验的负向迁移
学生虽然从第二学段才开始学习解方程,但学生从一年级开始已积累了与方程思想有关的符号、等式的意义等经验。笔者在教学完“等式的性质”后,请学生运用已有的经验自主探究出解方程的方法,收集学生作品进行统计分析后发现,77.5%的学生倾向于运用已有的解方程的雏形经验来解方程,这势必对学生学习利用等式的性质来解方程带来负面影响。
②学生嫌其书写格式麻烦
为尽量避免学生运用四则运算关系解方程经验的负向迁移,强化用等式的性质来解方程,教师往往要求学生写出利用等式的性质的思维过程,而这种形式上的烦琐又引起了学生心理上的反感。
(2)课程方面的原因
①解方程课时安排过少
新教材在编排上将解方程和列方程解决实际问题融合在一起,安排了10个例题的教学内容。学生既要学习列方程解决实际问题的策略,又要探索解方程的方法,这样的安排难点过于集中,影响了学生解方程技能的形成。
②难点突出又过于集中
教材的解方程教学,只安排了形如x±b=c、ax=b、x÷a=b、ax±b=c、ax±bx=c,而忽略了a÷x=b、a-bx=c、3x+6=4x-2等类型方程解法的教学,而在具体的问题解决中列出这样的方程是无法避免的。
二、小学高年级数学教学中强化方程思想的策略
1.在列方程教学中强化建模思想
(1)体会优势,让列方程成为学生的应然选择
①方法对比,在过程中感受方程建模思想的价值
学生从开始学习到列方程解决稍复杂的实际问题,会面临复杂的问题情境,学生运用算术思维解决问题受挫,冲突引发需求,此时教师引导学生运用方程建模的思想解决问题,学生经历了实现顿悟的过程,从而体验到方程分析法的优势。
②问题比较,在运用中感受方程建模思想的适用性
当学生在进行了一定的列方程解决问题的训练之后,也不可避免由算术思维的定势走向了方程分析法的定势。所以教师要通过设立对比性练习,让学生感悟到根据顺向思维能直接列出算式计算出结果的问题适用于算术法,而逆向思维的、数量关系隐蔽的问题应该尝试用列方程的方法来解决。
(2)重点突破,加强寻找等量关系的方法指导
教师要寻求合适的教学策略帮助或促进学生识别、分析问题中的数量关系,建构起问题中的等量关系,这是方程教学的关键。要注重从情境本身去建构等量关系,而不是只强调抽象的等量关系。
①抓关键句转译数学语言,确定等量关系
语言表达是完善思维活动过程的必要手段。方程分析法的显著优势是顺向思考,教师给予学生说的机会与时间,学生抓住关键语句将题中的事理按顺序说出,能进一步促使学生将生活情境转译成数量关系,这是学生把握等量关系的有效前提。
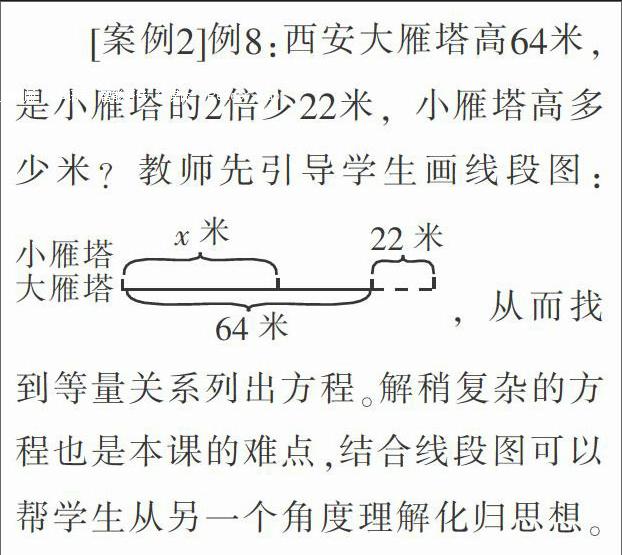
②数形结合有效表征问题,确定等量关系
学生对问题进行正确的表征,是有效解决问题的前提。在数学教学中要引导学生将问题中的信息用画线段图的方式进行表征。借助直观形象的线段图,学生能更容易找到等量关系,从而顺利实现方程的建模。
③根据常见的数量关系,确定等量关系
有些数量关系在生活中经常接触,学生比较熟悉。对于这样的数量关系,可以让学生在充分体验的基础上再进行抽象。在解决问题的应用中,教师要关注巩固常见的数量关系,这对帮助学生寻找等量关系有着至关重要的作用。
④把握不变量,确定等量关系
面对复杂的问题情境,学生往往会感到束手无策,不知如何确定等量关系式。笔者在教学中常利用“不变量”的思维,让学生通过“不变量”找出等量关系列出方程,这样就大大降低了教学的难度。
2.在解方程教学中强化化归思想
(1)运用操作原型,专项突破体会抵消思想。
学生在理解了等式的性质之后,教师引导学生利用等式的性质来解方程,发现学生在接受上有很大困难。仔细研究教材,再次发现学生缺乏消元的相关经验,特别是面对形式化的方程时,不知该如何消元,为何要消元。
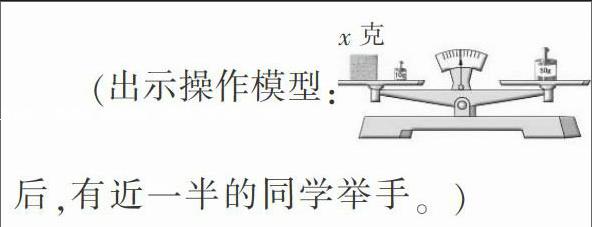
[案例1]教学x+10=15
师:你能运用自己的方法求出x的值吗?
(大多数学生运用四则运算的关系来求解,学生交流后,教师进一步引导。)
师:你能运用我们今天学习的等式的性质来解方程吗?
(只有少数几个同学举手)
师:有点困难,看老师为你提供的材料,能给你带来启发吗?
生1:我们可以将左边拿去10g,要使天平保持平衡右边也要拿去10g。
生2:我们将等式的左右两边都减10就可以了。
师:等式两边为什么要同时减去10呢?
生:这样就可以把x+10变成x,我们就可以求出答案了。
操作原型是跨越算理与算法之间的桥梁。教师注重拉长相关教学细节,以使学生操作本身所蕴藏的抵消思想得以逐步显性化。学生在操作的过程中,丰富了体验,顺利实现抵消经验的自然积淀。在此基础上,教师要加强抵消思想的专项训练,例如:x-15=60,x-15+15=60○□,以实现算法的自动化。
(2)延续利用画图,以用促算体会化归思想
新教材将方程教学与列方程解决问题融合在一起,在解决复杂问题时,很多教师都能引导学生画图来表征问题以实现方程的建模,但画图的价值也仅限于列方程。在实际教学中,笔者将实际问题的解决与解方程结合到一起,“以用促算”收到了良好的效果。
这样的微调更为直观形象,方程的运用本身促进了算法的内化,化归思想也能更容易为学生所理解。
(3)题型延伸类比,整体建构提升化归思想
小学高年级方程解法教学滞后于列方程解决问题的教学(前文已阐述),基于此问题,笔者将教材的结构再次进行了微调。在五年级下册学生学会简易方程之后,教师增加了两课时的求解复杂的方程(例如:(x-3)÷2=8,3x+6=4x-2)。教师引导学生经历求解复杂方程的过程,将利用等式性质求解与算术思维求解进行比较,学生真切地体会到运用等式的性质的优越性,增强了其利用化归思想解方程的能动性。教师注重引导学生反思解方程的过程,在不同类型方程解法的类比中进行整体建构,深层体悟化归思想的本质。
列方程解决问题是小学数学教学的难点,但教师过度热衷于将数量关系进行分类,会使学生陷入机械地列方程解决问题的解题套路中。在教学中,教师要多鼓励学生经历探究问题解决的过程,体会到方程是等价数学模型的内在本质,深刻领会建模思想和化归思想。只有这样,学生才能更好地掌握利用方程思想解决数学问题的方法。

