基于遗传算法的七自由度机器人轨迹规划

马丹妮, 李传江, 张自强

(1. 广东省电信规划设计院有限公司, 广东 广州 528000; 2. 上海师范大学 信息机电学院, 上海 201418)



基于遗传算法的七自由度机器人轨迹规划

马丹妮1, 李传江2, 张自强2

(1. 广东省电信规划设计院有限公司, 广东 广州 528000; 2. 上海师范大学 信息机电学院, 上海 201418)

针对七自由度串联机器人Robai Cyton Gamma 300轨迹规划问题，采用改进遗传算法规划机器人各关节的运动轨迹。利用D-H表示法建立起机器人末端执行器的位姿与参考坐标系之间的齐次变换矩阵，采用遗传算法优化BP神经网络求解机器人的运动学求逆解。利用5次B样条曲线在关节空间构造机器人各关节随时间变化的运动轨迹。在满足运动学约束条件下，对传统遗传算法在编码方式、遗传算子、交叉概率和变异概率等方面进行改进，对机器人各关节运动轨迹进行时间最优规划。运用Matlab对研究进行了仿真实验。结果表明,经改进遗传算法优化后的机器人运动轨迹时间明显缩短，各关节的角速度、加速度和加加速度曲线连续无突变，从而验证了该方法的有效性。

遗传算法； Robai Cyton Gamma 300机器人； Bezier曲线； 轨迹优化

0 引 言

机器人轨迹规划是指机器人运动过程中的运动轨迹，即运动时各关节的位移、速度、加速度随时间变化的曲线[1-2]。机器人的轨迹规划是机器人控制的基础，近年来是机器人领域的研究热点。

轨迹规划的性能指标有很多种，主要分为：时间最优轨迹规划[3]、能量最优轨迹规划[4]、冲击最优轨迹规划[5]以及混合最优轨迹规划[6]。其中，时间最优轨迹规划对提高机器人工作效率有重要意义，也一直是机器人轨迹规划研究的重点。国内外针对机器人的时间最优轨迹规划提出了许多不同的规划方法，主要有二次规划法[7]、动态目标规划法[8]、PID控制法[9]、迭代法[10]等。

本文以七自由度串联机器人Robai Cyton Gamma 300为研究对象，将时间最短作为轨迹优化目标，采用5次B样条曲线进行机器人各关节轨迹规划，在满足运动学参数的约束下，运用改进的遗传算法实现对运动轨迹的时间优化。实验结果表明，机器人运动总时间明显减少，经优化后机器人各关节的运动轨迹连续、无突变，从而验证了该算法的有效性和实用性。

1 Robai Cyton Gamma 300机器人的运动学分析

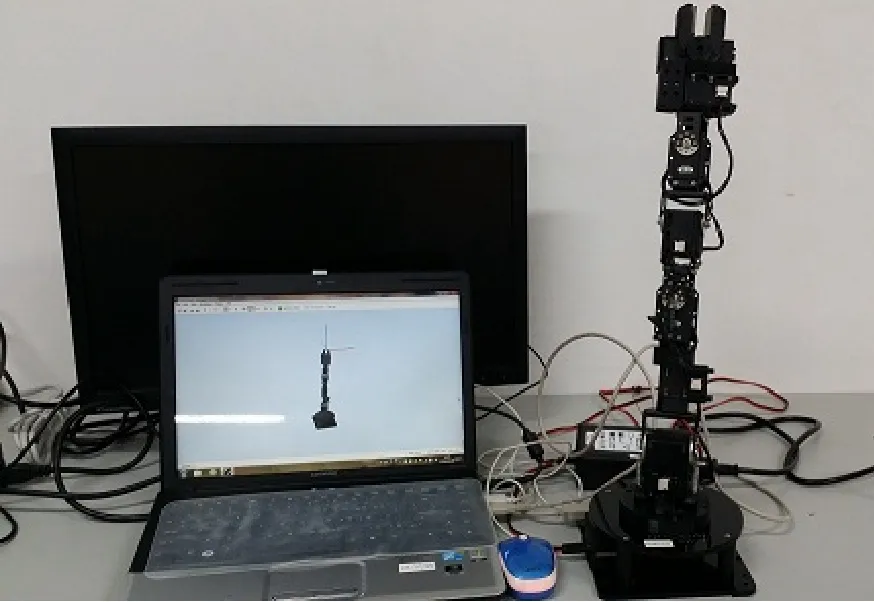
Robai Cyton Gamma 300是由美国宾夕法尼亚州的诺百公司生产的一种创新的七自由度机器人，与人的手臂结构相似，由7个转动关节(直流电机)串联而成。采用USB或RS485进行通信，具体的技术参数如下：结构形式为开环链式结构，负载能力300 g，重复定位精度±0.5 mm，最大展开半径48 cm，自身高度53.4 cm，自身质量1.2 kg，驱动方式为直流电机驱动，控制方式为PTP/CP，操作方式为示教操作，供电电源为12 V/2 A直流电源供电，工作环境温度20～35 ℃。位移范围:θ1=300°,θ2=210°,θ3=300°,θ4=210°,θ5=210°,θ6=210°,θ7=300°。利用机器人自带的开发软件Cyton Viewer采用D-H法建立机器人的连杆坐标系如图1所示，其D-H参数如表1所示。

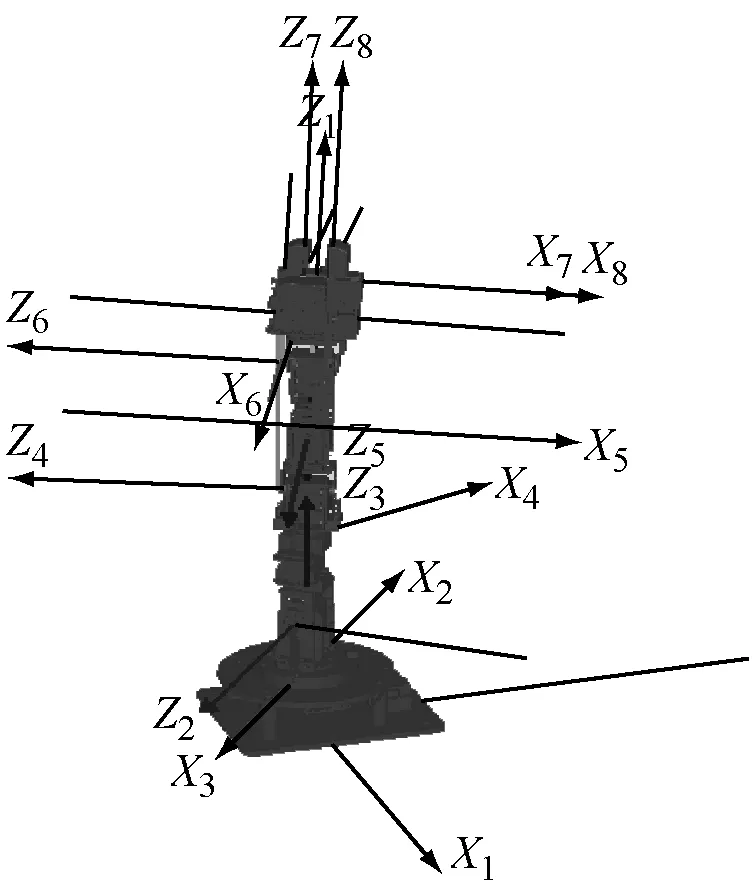
图1 Cyton Viewer中建立的机器人D-H坐标系

由图1知，机器人在几何结构上不满足pieper准则[11-12]，无法获得解析解，运动学方程的逆解是高度非线性方程组的求解问题。因此采用遗传算法优化BP神经网络的初始权值和阈值，使优化后的BP神经网络能更好地求解机器人的运动学逆解[13]：① 将神经网络的输入层、隐含层、输出层中全部权值和阈值作为种群个体；② 把BP神经网络的预测输出和期望输出之间的误差绝对值之和作为个体适应度值；③ 选择、交叉、变异等遗传操作。

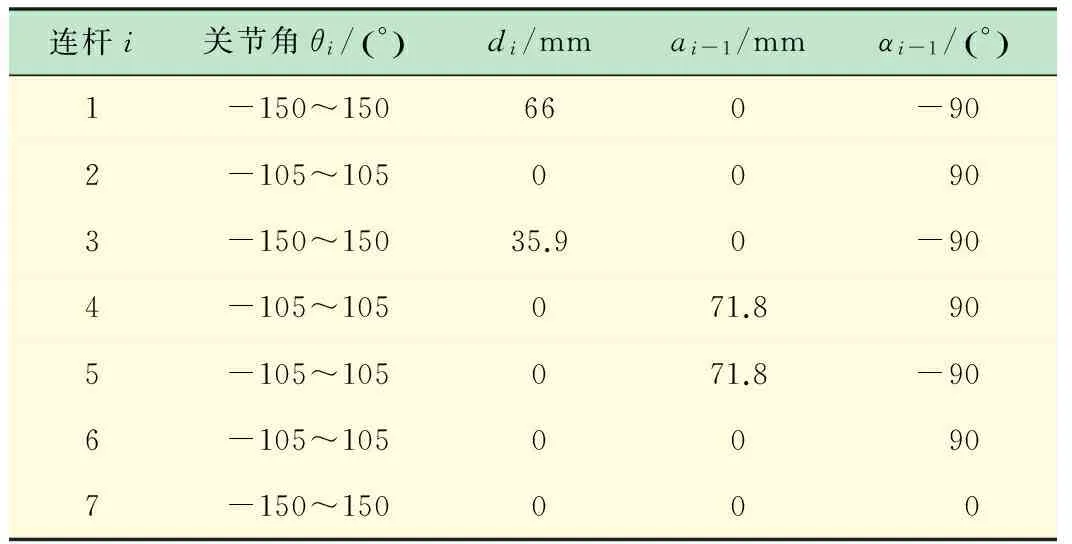
表1 Robai Cyton Gamma 300机器人的D-H参数

2 5次B样条曲线构造运动轨迹

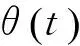
(1)

由deBoor算法[14]可以推导出：

(2)

(3)

式中：j=i-k+l,…,i。

(4)

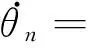
(5)

3 改进GA时间最优轨迹规划

3.1 运动学约束条件

在关节空间中，考虑各关节所能达到的最大速度、最大加速度以及最大加加速度的限制，因此定义各关节速度、加速度、加加速度的约束条件：

(6)

式中，i=0,1,…,n。

3.2 时间最优轨迹规划目标的建立

本文选择机器人运动时间最短作为5次B样条曲线轨迹优化的目标函数：

(7)

式中:T为机器人沿B样条曲线轨迹运动的总时间；hi为机器人沿每一段轨迹运动的时间；m为型值点的个数。

3.3 改进GA算法的轨迹优化

为了克服传统遗传算法的缺陷与不足，本文对其在编码方式、遗传算子、交叉概率和变异概率等方面进行改进：

(1) 采用实数编码。直接采用解空间的形式进行编码，能明确地表达出问题本来的意义，易于引入特定领域的信息，而且能大大缩短串长，无需频繁地编码解码，减少了遗传算法的计算量，提高了算法的效率。

(2) 采用排序选择法。将每一代种群中各个个体的适应度值进行排序，在排序的基础上进行选择操作，进而更方便、高效地选择出适应度高的个体参与下一步的交叉、变异等遗传操作。

(3) 采用自适应的交叉概率和变异概率。对于适应度高于平均适应度的个体，相对应的交叉概率和变异概率降低；而对于适应度低于平均适应度的个体，相对应的交叉概率和变异概率提高，这样避免了算法陷入局部最优，从而提高了全局寻优能力。具体的调整公式为[15]：

(8)

(9)

式中:Pc1=0.9,Pc2=0.6,Pm1=0.1,Pm2=0.01;fmax为种群中最大适应度值;favg为种群的平均适应度值;f′为相互交叉两个个体中较大的适应度值;f为变异个体的适应度值。

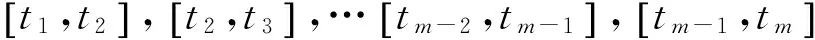
(10)

式中,ti为机器人运动到该节点处的时刻。

实现步骤：

(1) 编码。 采用实数编码方式将机器人沿每一段曲线运动所需时间编码成遗传算法所需要的染色体；

(2) 种群初始化。在每段曲线运动时间hi的取值范围内，随机产生一定数量的个体；

(3) 适应度函数。

(11)

式中:hmax为给定范围内hi的最大值。该适应度函数能保证不满足约束条件的个体被赋予最小的适应度值。

(4) 选择。对每代种群中的个体按适应度值由大到小排序，适应度值高的个体优先进行交叉、变异等遗传操作。

(12)

式中：k为排序操作后个体适应度值在序列中所处的位数。

(5) 交叉。选用线性交叉算子。假设Xk、Yk为两个父代个体，经过算术交叉操作，产生了新的子代个体Xk+1、Yk+1：

(13)

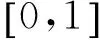
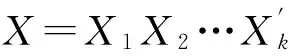
(14)

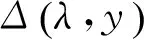
(15)

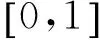
4 仿真实验验证

4.1 GA优化BP神经网络求运动学逆解

用向量θ=(θ1,θ2,θ3,θ4,θ5,θ6,θ7)表示Cyton Gamma 300机器人完成任意动作的各关节变量θ，用向量X=(nx,ny,nz,ox,oy,oz,ax,ay,az,px,py,pz)表示机器人末端执行器的位姿。在其运动空间内任取400组末端执行器位姿为输入变量input，和与之对应的各关节变量为输出变量output，其中300组数据作为BP网络的训练样本，100组数据为预测样本。训练网络的输入变量P为12×300维的矩阵，输出变量T为7×300维的矩阵。BP网络的输入层神经元个数为12，输出层神经元个数为7。根据隐层设计的经验公式得到隐层神经元个数为12。BP神经网络和GA优化的BP神经网络的训练结果分别如图3、图4所示。

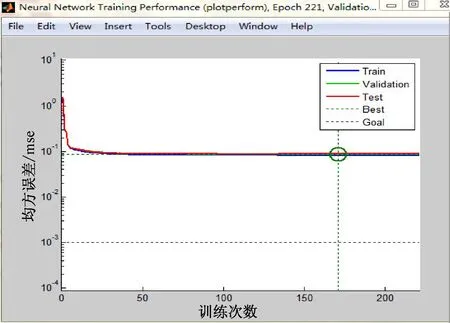
图3 BP网络训练结果

通过分析和训练结果可知，经过GA优化后的BP神经网络能得到更好的网络初始权值和阈值，训练次数由221次减少到112次，收敛速度明显提高，预测误差由0.086 7减小到0.065 969，网络预测误差也减小了。实验证明,经优化的BP神经网络能够更准确、快速地求解机器人的各关节变量。

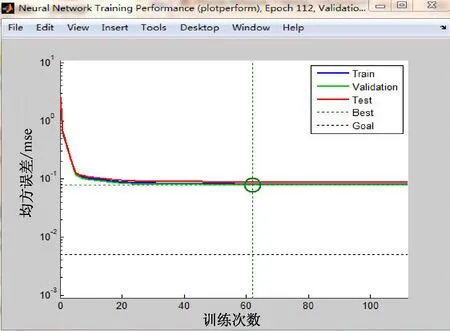
图4 经遗传算法优化后训练结果

4.2 改进GA优化机器人运动轨迹

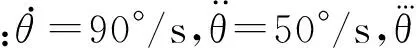
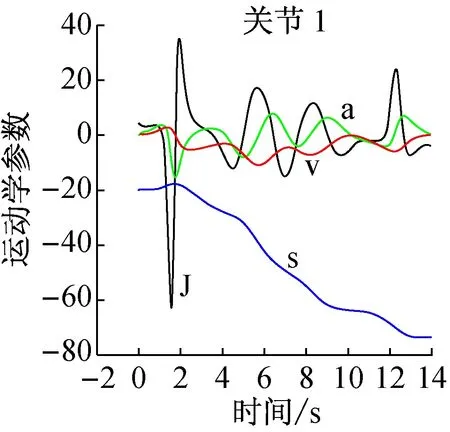
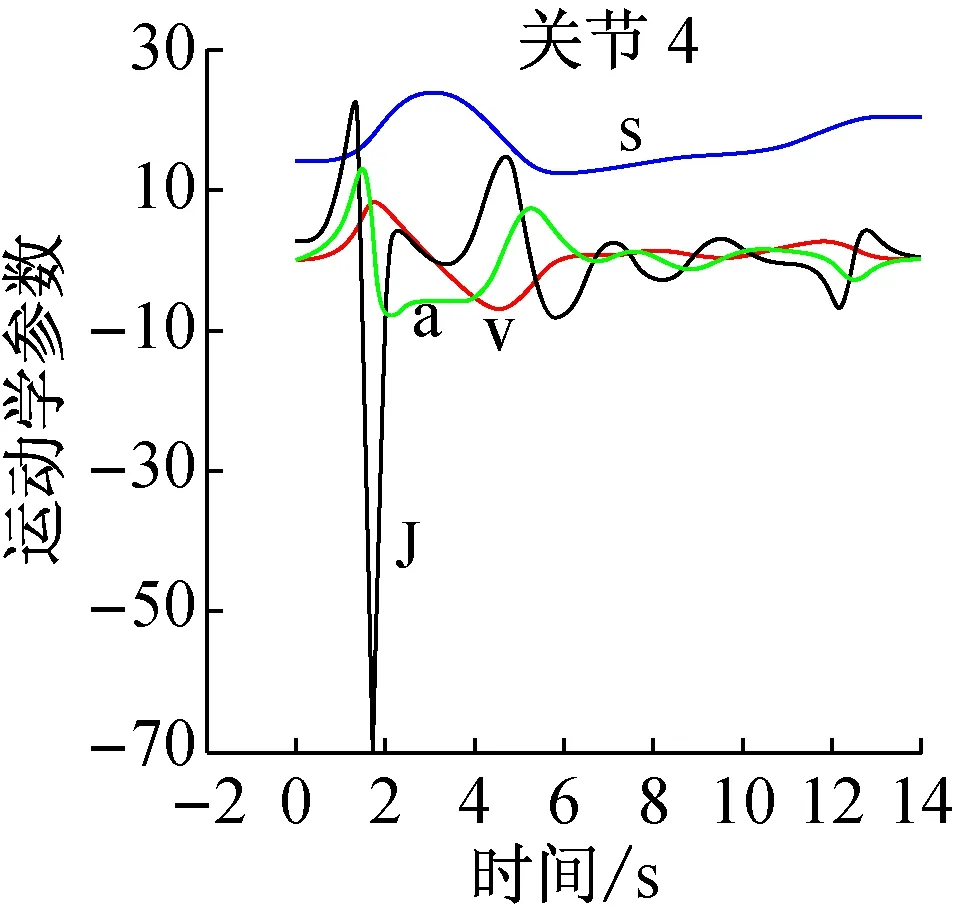
由表2中第6次优化结果可得出，采用改进遗传算法，在满足机器人运动学约束条件下，对5次B样条各关节运动轨迹进行时间优化，总时间由初始状态的18 s缩短到14.003 9 s，缩短了3.996 1 s。经改进遗传算法优化后的时间序列生成5次B样条运动轨迹见图6(图中：s代表关节角位移，mm;v代表关节角速度，mm/s; a代表关节角加速度，mm/s2; J代表关节角加加速度,mm/s3)，优化后的各关节的位移、速度和加速度曲线光滑平稳，加加速度曲线连续无突变。

5 结 语

本文以七自由度串联Robai Cyton Gamma 300机器人为研究对象，采用5次B样条曲线构造运动轨迹。通过对传统遗传算法在编码方式、选择算子、交叉概率和变异概率等方面作出改进，以运动时间最短为优化目标，在Matlab中进行轨迹优化仿真实验，结果表明机器人的运动总时间由初始状态的20 s缩短到14.003 9 s，达到了运动轨迹时间优化的目标。经优化后的机器人各关节的角速度、加速度和加加速度变化曲线连续无突变，从而验证了该方法的可靠性和有效性。

[1] Saeed B Niku. 机器人学导论——分析.控制及应用[M]. 2版. 北京：电子工业, 2013：136-241.

[2] 张 涛. 机器人引论[M]. 北京：机械工业出版社, 2010：303-512.

[3] Lin C C, Chen M Y. Intelligent mobile mechanical arm design[C]//System Science and Engineering (ICSSE), 2010 International Conference on. IEEE, 2010: 136-141

[4] Quigley M, Asbeck A, Ng A. A low-cost compliant 7-dof robotic manipulator[C]//Robotics and Automation (ICRA), 2011 IEEE International Conference on. IEEE, 2011: 6051-6058.

[5] Chettibi T, Lemoine P. Generation of Point to Point Trajectories for Robotic Manipulators Under Electro-Mechanical Constraints[J]. International Review of Mechanical Engineering, IREME, 2007(2):131-143.

[6] Sakai S, Xu C, Ming A,etal. Motion planning for a high-speed manipulator with mechanical joint stops based on target dynamics and PCH system[C]// Intelligent Robots and Systems, 2009. IROS 2009. IEEE/RSJ International Conference on. IEEE, 2009:279-284.

[7] Pchelkin S S, Shiriaev A S, Robertsson A,etal. Integrated time-optimal trajectory planning and control design for industrial robot manipulator[C]//Intelligent Robots and Systems (IROS), 2013 IEEE/RSJ International Conference on. IEEE,2013:2521 - 2526.

[8] Ghasemi M H, Kashiri N, Dardel M. Time-optimal trajectory planning of robot manipulators in point-to-point motion using an indirect method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2012, 226:473-484.

[9] Muller P A, Boucherit R, Liu S. Smooth and time-optimal trajectory planning for robot manipulators[C]//American Control Conference on. IEEE, 2012:5466 - 5471.

[10] 刘松国. 六自由度串联机器人运动优化与轨迹跟踪控 制研究 [D]. 杭州: 浙江大学, 2009.

[11] 余 阳, 林 明, 林永才. 基于混合遗传算法的工业机器人最优轨迹规划[J]. 计算机工程与设计, 2012, 33(4):1574-1580.

[12] 钱东海, 马文罗, 汪建伟,等. 多约束条件下的机器人时间最优轨迹规划[J]. 制造业自动化, 2011, 33(11):1-5.

[13] Lee J D, Heshmati A. Solution of Inverse Kinematics for SCARA Manipulator Using Adaptive Neuro-Fuzzy Network[J]. International Journal on Soft Computing, 2011, 2(4):501-504.

[14] Pérez Bailón W, Barrera Cardiel E, Juárez Campos I,etal.Mechanical Energy Optimization in Trajectory Planning for Six DOF Robot Manipulators Based on Eighth-Degree Polynomial Functions and a Genetic Algorithm[C]//Electrical Engineering,Computing Science and Automatic Control Conference on. IEEE,2010:466 - 451.

[15] Frederik Debrouwere, Wannes Van Loock, Goele Pipeleers,etal.Time-Optimal Path Following for Robots with Trajectory Jerk Constraints using Sequential Convex Programming[C]//2013 IEEE International Conference on Robotics and Automation (ICRA) Karlsruhe,Germany,May 6-10, 2013:1916-1921.

[16] Liu H, Lai X, Wu W. Time-optimal and jerk-continuous trajectory planning for robot manipulators with kinematic constraints[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(2):309-317.

Seven Degree of Freedom Robot Trajectory Planning Scheme Based on Improved Genetic Algorithms

MADan-ni1,LIChuan-jiang2,ZHANGZi-qiang2

(1. Guangdong Planning and Designing Institute of Telecommunications CO.LTD, Guangzhou 528000, China; 2. College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 201418, China)

To solve trajectory planning problem of seven degree of freedom serial robot called Robai Cyton Gamma 300, an improved genetic algorithm was applied to plan robot trajectory of each joint. First, D-H notation was used to establish homogeneous transformation matrix between the actuator's posture at the end of the robot and the reference coordinate system. And genetic algorithm was used to optimize the BP neural network to solve the kinematics inverse solution of robot. Then, five B spline curve was applied in the joint space of each joint’s motion trajectory. Finally, under the condition of kinematic constraint, traditional genetic algorithm was improved on mode of coding, genetic operators, crossover probability and mutation probability, etc, to realize the time optimal planning. By conducting the simulation experiment on Matlab, the results showed the trajectory time of robot was optimized obviously by improved genetic algorithm. Angle velocity and the acceleration and jerk of each joint were continuous, it proved the effectiveness of the proposed method.

genetic algorithms(GA); Robai Cyton Gamma 300 robot; Bezier(B) spline curve; trajectory optimization

2015-12-02

上海市科委基金资助项目(11510502400)

马丹妮(1990-)，女，河南新县人，硕士，主要研究方向为嵌入式系统与自动化装置。

Tel.:021-57122955； E-mail:nini502327489@126.com

张自强(1958-)，男，河南洛阳市人，教授，硕士生导师，主要研究方向为自动化控制。

Tel.:021-57122955； E-mail:zhzq@shnu.edu.cn

TP 273

A

1006-7167(2016)09-0033-05