亏群同构于×Z3的块代数的结构

戴康顺，杨 胜

（温州大学数学与信息科学学院，浙江温州 325035）

戴康顺，杨 胜

（温州大学数学与信息科学学院，浙江温州 325035）

假设G是一个有限群，p是一个固定的素数，B是群G的一个p块，且B的一个亏群为D.在模表示理论中，当块B的亏群D给定时，如何确定块B的结构是一个主要问题.这里块B的结构，是指属于块B的不可约模指标个数以及不可约常指标个数.在G是 3-可解的或者亏群D是正规的前提下，给出了亏群D同构于的块代数结构，计算出了k（B）和l（B）这两个重要的块不变量.

块；子对；亏群

在有限群模表示理论中，一个经典问题是确定给定亏群的块代数结构.Dade［1］在 1966年确定了亏群为循环群的块代数结构.对循环块的研究之所以能够取得相当彻底的成果，在很大程度上依赖于以下事实：一个块是有限表示型的（即循环块中不可分解模的同构类只有有限多个），当且仅当这个块的亏群是循环群［2］.亏群非循环的p-块不是有限表示型的，这样的块当中不可分解模的同构类非常复杂，难以应用Green对应来解决问题.近些年，确定给定亏群的块代数结构这个课题取得了一些结果.比如亏群为二面体群、广义四元数群、拟二面体群、极小非交换的2-群、亚循环2-群等2-块，确定了块的结构［3］.但是当亏群非循环且p是一个奇素数时，相关研究不多.在计算块不变量时，Brauer的著名公式是很有用的，其中.Kiyota［5］在1984年基本确定了亏群为9阶初等交换群的块代数结构，他的文章的关键工具就是 Brauer的著名公式.在G是3-可解的或者亏群D是正规的前提下，当，确定了这个块的结构.

本文受Kiyota的文章［5］的启发，在G是3-可解的或者亏群D是正规的前提下，当D同构于时，计算出了k（B）和l（B）这两个重要的块不变量.

1 主要结论

进一步，

2 主要结论的证明

引理1［4］假设G是一个有限群，p是一个素数，B是G的一个p-块，则，其中.

引理2［6］G是一个有限群，p是一个素数，B是G的一个p-块，D为块B的亏群.如果D为交换群，则，等号成立当且仅当.

引理3［6］G是有限群，p是素数，B是G的一个p块，B的亏群D是阶为 pd的交换群.如果D的秩为2，则.

引理4［7］G是有限群，p是一个素数，B是G的一个p块，当p=3时，k0（B）=0（mod3）.

引理5［5］B是G的一个p块，且亏群D交换.是一个B-西罗子对.假设G是p-可解的或，则有等式，这里等式右边指的共轭类数.

另外，如果下列条件成立，则上述不等式的等号成立.

设G是一个有限群，p为一个素数，D为一个p-块，假定p=3和，在这种情况下得到了k（B）和l（B）.

因此，

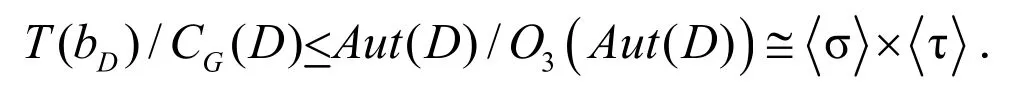
得到：

故，

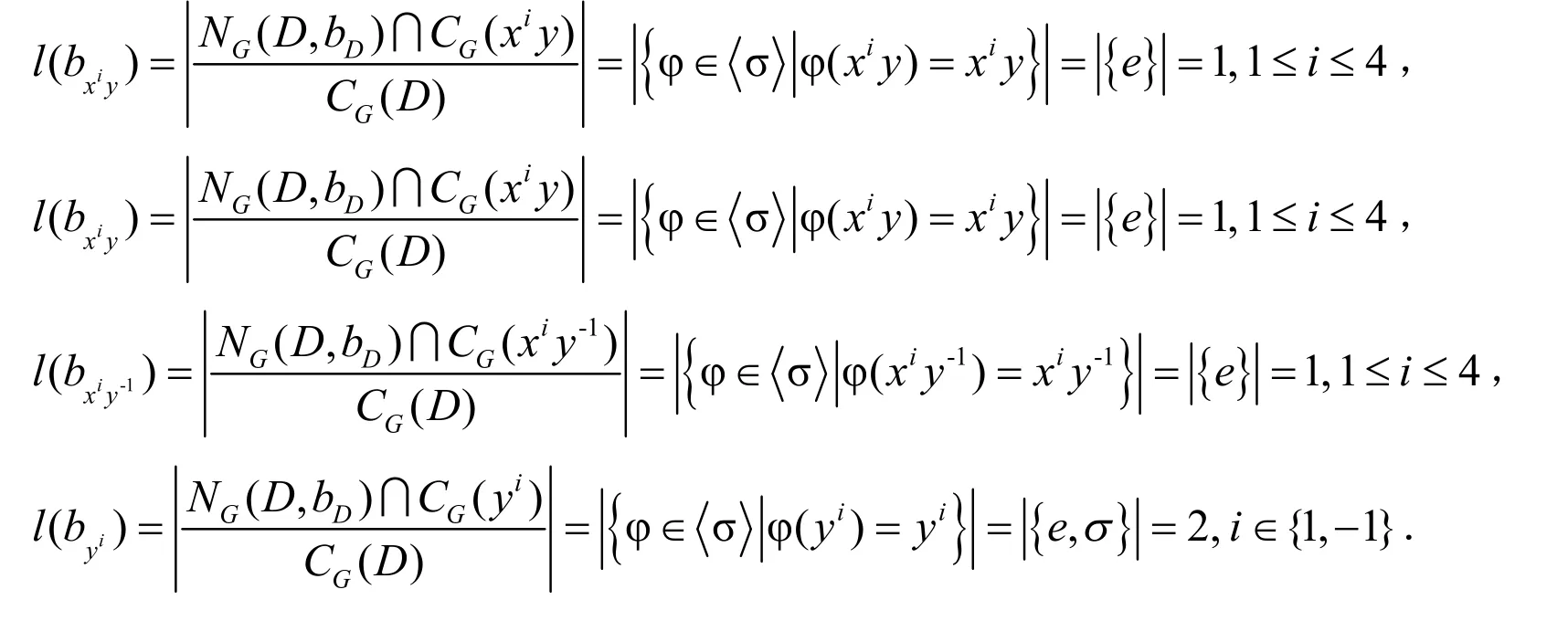
因此，

假设ω∈D，与（a）的证明相似，舒尔乘子是平凡的，在此条件下是 3-可解的或，则：

故，

因而，

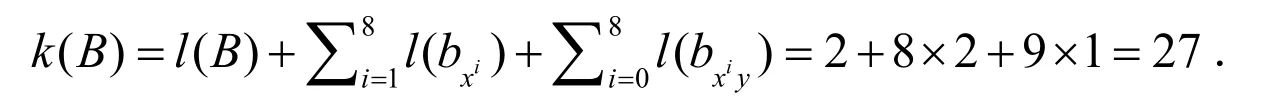
假设ω∈D，与（a）的证明相似，舒尔乘子是平凡的，在此条件下是 3-可解的或，则：

故，

因而，

假设ω∈D，与（a）的证明相似，舒尔乘子是平凡的，在此条件下是3-可解的或，则：

故，

3 结 论

本文研究了确定给定亏群的块代数结构问题.在G是3-可解的或者亏群D是正规的前提下，当D同构于时，计算出了k（B）和l（B）这两个重要的块不变量.

［1］ Dade E C. Blocks with cyclic defect groups ［J］. Ann of Math， 1966， 84： 20-48.

［2］ Martin I I. Characters theory of finite groups ［M］. New York： Academic Press， 1976： 6-12.

［3］ Sambale B. Blocks of finite groups and their invariants ［M］. Berlin： Springe， 2014： 4-20.

［4］ Brauer R. Zur Darstellungstheorie der gruppen endlicher osdnung II ［J］. Math Z， 1967， 72： 895-925.

［5］ Kiyota M. On 3-blocks with an elementary abelian defect group of order 9 ［J］. J Fac Sci Univ Tokyo Sect IA Math，1984， 31（1）： 33-58.

［6］ Brauer R. On blocks and sections in finite groups II ［J］. American Journal of Mathematics， 1967， 90（3）： 895-925.

［7］ Landrock P. On the number of irreducible character in a 2-block ［J］. J Algebra， 1981， 68： 426-442.

The Structure of Block Algebra with a Defect Group D×Z3

DAI Kangshun， YANG Sheng
（College of Mathematics and Information Science， Wenzhou University， Wenzhou， China 325035）

Supposed that G be a finite group and p be a fixed prime number， B is a p-block of group G with defect groupD. It is a major problem in modular representation theory to determine the structure of B when the defect group D is given. The structure of B here refers to the number of irreducible modular characters as well as the number of irreducible ordinary characters. The algebraic structure of the block algebra with a defect groupis given under the premise that G is 3-solvable or the defect group D is normal. The two important invariants associated with the block algebra such as k（B）and l（B）are calculated.

Block； Sub-pair； Defect Group

O152

A

1674-3563（2016）03-0015-06

10.3875/j.issn.1674-3563.2016.03.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：封毅）

2015-05-28

国家自然科学基金（13101193）；浙江省新苗计划（2013R424012）

戴康顺（1992- ），男，浙江衢州人，研究方向：基础数学