基于形函数的多层粘滞减震结构优化

裴 少 帅

(同济大学土木工程学院，上海 200092)



基于形函数的多层粘滞减震结构优化

裴 少 帅

(同济大学土木工程学院，上海 200092)

分析了粘滞减震结构等效层间剪切角刚度，提出了基于形函数的优化方法，通过算例，论证了该方法的适用性，并且得到了粘滞阻尼器优化布置的规律，有利于充分发挥粘滞阻尼器的耗能能力。

粘滞阻尼器，形函数法，剪切角刚度

0 引言

为了粘滞阻尼器有效发挥其耗能能力，提升结构响应控制效果，国内外很多学者对粘滞阻尼减震结构的设计方法和粘滞阻尼器的优化布置进行了大量的研究。Takewaki[1]利用最速下降法对各层粘滞阻尼器的粘滞阻尼系数进行了优化；N.Wongprasert等[2]利用遗传算法对各层阻尼器个数进行优化。李波等结合抗震设计规范反应谱给出了一个附加非线性流体粘滞阻尼器结构的抗震设计方法；翁大根等[3]提出了一种针对附加粘滞阻尼器减震结构的实用设计方法；孙传智等[4]研究了基于响应面法进行减震结构非线性粘滞阻尼器参数优化设计的方法。Richard J.Balling等[5]利用遗传算法对全铰接屈曲约束支撑进行优化研究，并得出各层屈曲约束支撑截面面积沿楼层为直线分布。

本文结合已有研究工作，提出了基于形函数的优化方法，有效的简化了粘滞阻尼器优化布置问题，并且通过算例论证了该方法的适用性，得到了阻尼器优化布置的规律。

1 粘滞减震结构等效层间剪切角刚度

在粘滞减震结构中，粘滞阻尼器和主结构共同参与抗侧，因此在粘滞减震结构优化过程中，必须综合考虑这两方面抗侧参数才能得到阻尼器优化布置的规律。

粘滞阻尼器在建筑结构中只提供阻尼不提供刚度，本文主要研究线性粘滞阻尼器的优化布置，其阻尼力表达式见式(1)：

Fd=Cd·v(t)

(1)

当线性粘滞阻尼器两端的相对运动为简谐运动时，即u(t)=U·sin(ω·t)，则v(t)=ω·U·cos(ω·t)，将其代入式(1)，阻尼力表达式可转化为式(2)，《被动减震结构设计·施工手册》称Cd·ω为粘滞阻尼器损耗刚度。

Fd=Cd·ω·U·cos(ω·t)

(2)

考虑到粘滞阻尼器在减小层间剪切位移中的贡献，本文提出了减震结构等效剪切层间刚度的概念，减震结构等效层间剪切刚度=主结构层间剪切刚度+粘滞阻尼器损耗刚度，表达式见式(3)：

ks,eq=kf+Cd·ω

(3)

2 基于形函数的优化方法

线性粘滞阻尼器优化布置问题为：多遇地震下减震结构层间位移角小于限值的同时，各层线性粘滞阻尼器阻尼系数之和最小。

Js,eq,i=ks,eq,i·hi

(4)

本文借鉴Richard J.Balling[5]的研究，提出了一种基于形函数的优化方法，简称形函数法。形函数法是假定减震结构等效剪切角刚度随楼层的分布为直线，即Js,eq,i=f(i)，形函数f(i)是关于i的一次函数，其表达式为式(5)：

(5)

结合式(3)～式(5)，第i层粘滞系数Cd,i可用式(6)计算：

(6)

其中，ω1为主结构一阶自振频率。

粘滞阻尼器优化布置问题数学模型表达如式(7)所示：

(7)

上述将优化粘滞阻尼器粘滞系数Cd,i转化为优化形函数系数d和β，从而实现粘滞阻尼器最优布置的过程称为形函数法，将直接以每层粘滞阻尼系数Cd,i作为优化变量的优化过程称为直接优化。

3 算例分析

3.1 算例结构

本节算例采用4层钢框架结构，跨度为6.4 m，层高为4 m，多层钢框架结构在水平地震作用下结构侧向变形以剪切变形为主，所以结构地震响应分析采用剪切层模型。算例采用的四个结构的质量和层间剪切刚度如表1所示。

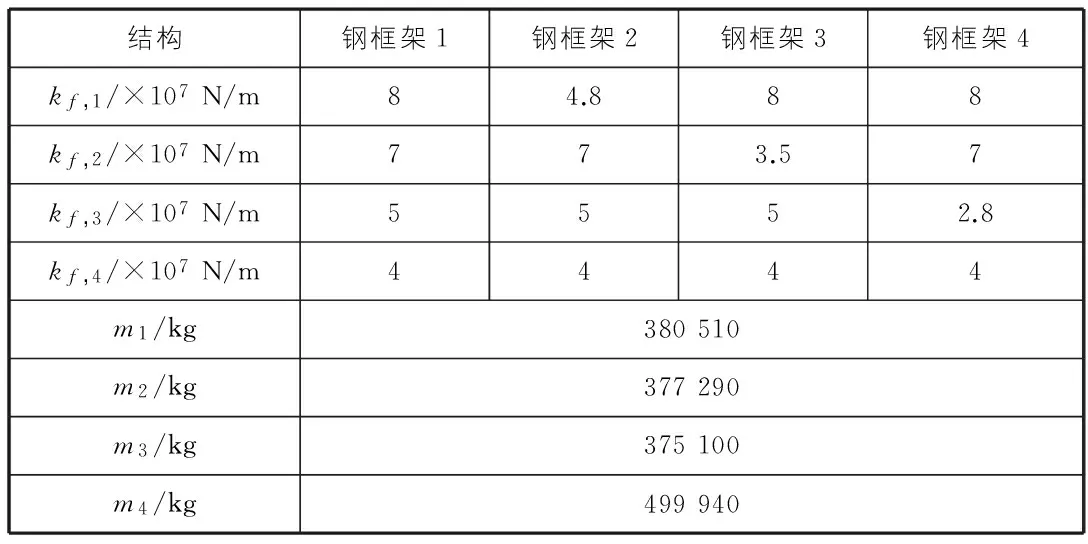
表1 结构刚度与质量

3.2 算例工况

为论证形函数法的适用性，本文共建立了4个工况(如表2所示)进行算例分析。本文算例地震烈度取为9度，场地为Ⅱ类场地第三组，原结构阻尼比为ξ=0.02，多遇地震下层间位移角限值[θ]=4×10-3。各工况所用地震记录的名字和峰值加速度如表2所示，表中还包含了加速度峰值缩放系数。

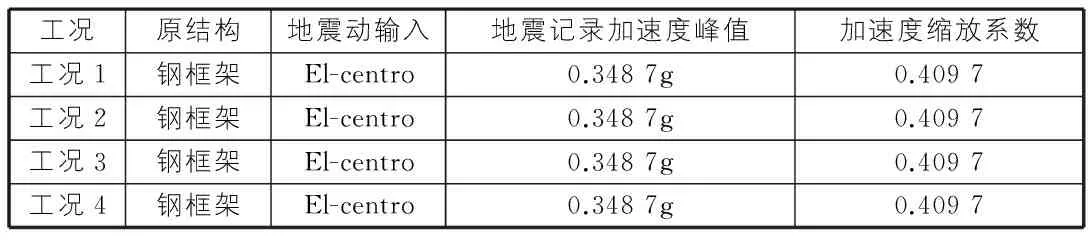
表2 各算例工况详情

3.3 ANSYS时程分析与优化

由于粘滞阻尼减震结构在利用反应谱分析时误差较大，因此本文利用ANSYS时程分析求解结构地震响应。利用ANSYS中Combin14单元和Mass21单元模拟线性粘滞阻尼减震结构，Combin14可定义水平方向的刚度和阻尼系数，Mass21可定义水平方向的质量。

本文利用ANSYS自带优化模块求解上述优化问题，ANSYS优化模块包括零阶算法和一阶算法。零阶算法属于因变量逼近，计算精度一般适用于大多数问题，计算速度比一阶快；一阶算法属于因变量导数逼近，精度较高，计算速度较慢。综合比较两个算法的优劣，本文选取零阶算法求解上述优化问题。

4 结果与讨论

4.1 收敛性分析

表3中，工况4迭代次数结果表示用直接优化布置粘滞阻尼器时，迭代并不收敛，而表3中形函数法迭代次数结果表示对于不同结构，形函数法迭代总会收敛。形函数法在减少设计变量的同时，改善了运用ANSYS零阶算法求解时的收敛性。

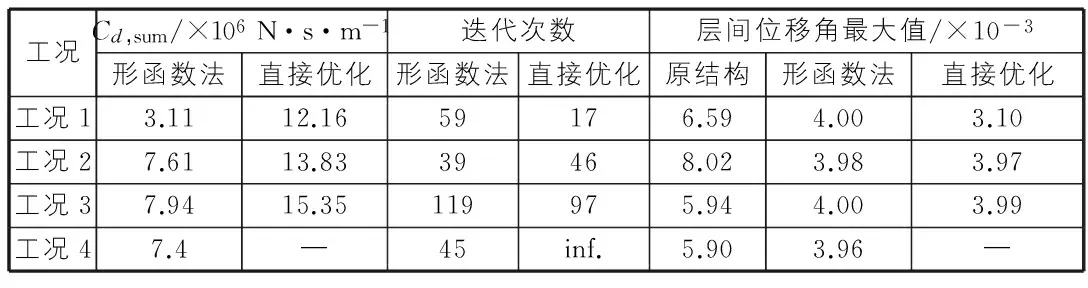
表3 各工况优化结果

4.2 形函数法的有效性

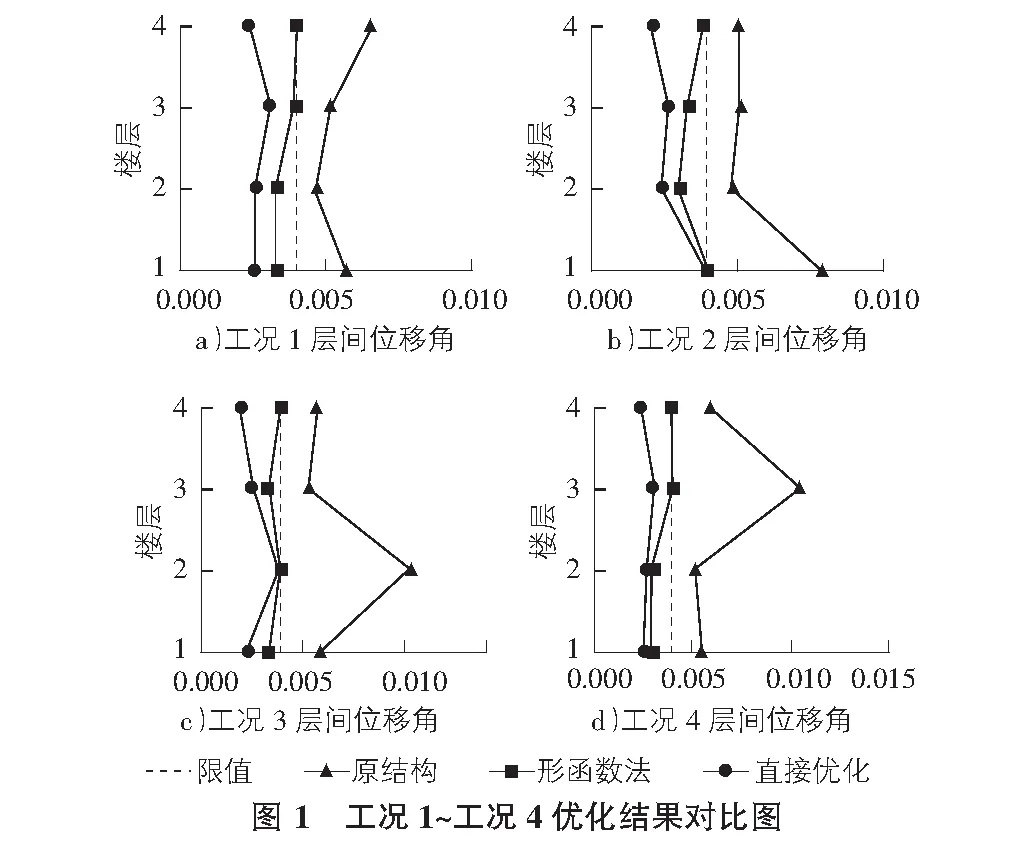
表3和图1中层间位移角项显示，各工况下利用形函数法优化得到的粘滞阻尼减震结构层间位移角最大值都不大于限值，且各层层间位移角比较均匀的分布在限值附近，说明形函数法能够得到效率较高的粘滞阻尼器布置形式。对于ANSYS零阶优化算法来说，利用形函数法优化布置粘滞阻尼器的结果比直接优化效果要好，且阻尼器分布效率较高。

5 结语

本文结合线性粘滞阻尼器恢复力模型，提出了等效层间剪切刚度的概念。同时本文提出一种基于形函数的优化方法，该方法假定减震结构等效层间剪切角刚度与楼层数之间的关系为直线函数关系，形函数法将附加粘滞阻尼器减震结构的阻尼器优化布置问题转化为形函数系数优化问题，并通过算例对形函数法的适用性和粘滞阻尼减震结构减震规律进行了分析，结论如下：

1)基于形函数的优化方法能够很好的解决粘滞阻尼器优化布置的问题，使得结构层间位移角能够均匀的分布在限值附近，并且小于限值。

2)无论主结构是否有薄弱层，减震结构等效层间剪切角刚度沿楼层为直线分布时，粘滞阻尼器的布置是效率较高的。

3)形函数法相比于直接优化，减少了设计变量的个数，提高了优化的效率。

[1] I.Takewaki.Optimal damper placement for critical excitation [J].Probabilistic Engineering Mechanics,2000(15):317-325.

[2] N.Wongprasert,M.D.Symans.Application of a Genetic Algorithm for Optimal Damper Distribution within the Nonlinear Seismic Benchmark Building[J].Journal of Engineering Mechanics,2004,130(4):401-406.

[3] 翁大根,张 超,吕西林，等.附加粘滞阻尼器减震结构使用设计方法研究[J].震动与冲击，2012，31(21):80-88.

[4] 孙传智,李爱群,缪长青,等.减震结构粘滞阻尼器参数优化分析[J].土木建筑与环境工程,2013,35(1):80-85.

[5] R.J.Balling, P.W.Richards. Design of Buckling-Restrained Braced Frames Using Nonlinear Time History Analysis and Optimization[J].Journal of Structural Engineering,2009,135(5):461-468.

Optimization of structures with supplemental viscous damping based on shape function

Pei Shaoshuai

(CollegeofCivilEngineering，TongjiUniversity，Shanghai200092，China)

Analyzes the equivalent shearing angle stiffness of viscous dampling structure. The shape function based optimization method proposed in this paper, the numerical examples verify the applicability of this method and obtain the optimum installation law of viscous dampers, play the fall role the viscous dampers’ energy consumption capacity.

viscous damper, shape function, shear angle stiffness

1009-6825(2016)11-0041-02

2016-02-01

裴少帅(1990- )，男，在读硕士

TU352

A