间歇式混合器混合性能研究及混合性能评价指标体系构建
李青寰,毕超
(北京化工大学 机电工程学院,北京 100029)
Li Qinghuan, Bi Chao
( Beijing University of Chemical Technology, Beijing 100029, China)
间歇式混合器混合性能研究及混合性能评价指标体系构建
李青寰,毕超
(北京化工大学 机电工程学院,北京 100029)
对近年来针对间歇式混合器混合性能研究的文献进行总结,归纳混合器转子结构和工艺条件对混合器混合性能的影响规律。并从数值模拟统计分析角度分析构成混合器混合性能评价指标体系中各个指标的应用情况。综述内容对混合器的优化设计和数值量化评价将有一定指导意义。
间歇式混合器;混合性能;数值模拟;评价体系
间歇式混合器广泛应用于橡塑工业[1~3]、食品制造[4~6]以及药物研究[7]等领域。该类混合器多以双转子类混合器为主,其典型的应用就是哈克流变仪的混炼部件。在基础实验探究中,通常用于混合两种及两种以上组分以组成共混物。其混合机理集中于物料层流剪切、拉伸流动、分布混合、分子扩散以及分散混合[8~9]。目前,针对间歇式混合器的研究是混炼装备研究热点之一。其中,混合器的优选以及混炼工艺的优化是研究者主要的工作。同时,随着计算流体力学的发展,数值模拟的统计学结果也逐渐成为评定混合器混合性能的重要手段。
本文将近年来针对间歇式混合器混合性能研究的文献进行总结,归纳混合器转子结构和工艺条件对混合器混合性能的影响规律。并从数值模拟统计分析角度介绍分析构成混合器混合性能评价指标体系中各个指标的应用情况。本文综述内容对混合器的优化设计和数值量化评价将有一定指导意义。
1 间歇式混合器混合性能研究现状
针对间歇式混合器混合性能的研究主要集中在类型对比、转子结构优选及操作工艺优化等方面。
1.1 类型对比
不同类型混合器的混炼性能存在较大差异。从混合器内转动部件数量角度来看,目前常用的混合器多以具有两个运动部件的双转子混合器为主。在Connelly等人[5]的研究中发现,与单转子混合器相比,基于全啮合几何学设计的同向旋转双转子混合器具有更好的混合能力。但是他们也指出,该类混合器流场区域内存在混合性能相对较弱的区域。从转子相对运动方向来看,在我们的研究中[10]对比了非啮合异向向外、异向向内和同向三种转子相对旋向对混合性能的影响。由于同向旋转工况可以使得混合器始终保持左右两腔内物料的交换,故此同向旋转工况模式下所得共混物的均匀性最佳。
1.2 转子结构的优选
改变转子结构是改善混合腔内流体流动形式的有效方法之一。性能优异的转子可以提供更大的剪切应力,更高强度的拉伸流动,可以使混合的有效面积增大,减小死区的面积。A. Chaisuriyathepkul等人[1]指出转子结构设计中考虑物料的轴向流动,可能为流体提供更高的压力从而使得流体中产生更多的拉伸流动。他们在NR/EPDM共混物制备中对比了如图1所
示的两种转子。结果表明,与全由啮合块组成的MX1型转子相比,两侧安装能够使物料向中间啮合块区域流动的螺纹元件的MX2型转子的混合能力较高。
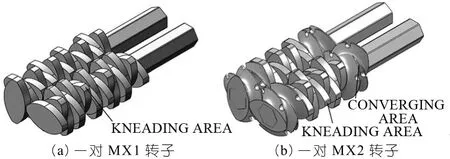
图1 文献[1]中的啮合同向间歇式混合器的转子结构
此外,转子截面形状的影响也是不可忽视的。S.A. Salahudeen等人[2]在非啮合异向混合器中分别安装Cam、Banbury和Roller三类转子(见图2)。综合考虑混合腔内流动模式、分布混合和混合效率来看,Roller转子的混合效果最好,Banbury次之,Cam最差。这与不同转子几何造型所对应的有效混合面积密切相关。

图2 文献[2]中的转子结构
1.3 操作工艺的影响
间歇式混合器的操作工艺条件通常包括转子转速、混合时间和填充率等。调整操作工艺参数是改善混合器混合性能的有效途径。
1.3.1 转子转速/速比的影响
转速不仅是影响混合性能的关键因素之一,同时还是影响剪切生热的主要因素。在定速比为3∶2的情况下,S. A. Salahudeen等人[3]研究了转速对混合性能的影响。他们指出在相同的混炼时间内,较低的转速会导致混合区域内拉伸强度相对较低,剪切生热现象相对较小;而过高的转速会在提升混合区域内拉伸强度的同时,产生过高的剪切热。他们还指出由于混合效率为拉伸率与黏性耗散率之比,聚合物加工过程中的能量耗散过大,则混合效率也会降低。在我们之前的研究中[11],针对转子速比对混合性能影响进行了研究。保持一侧(A侧)转速恒定,通过改变另一侧(B侧)转速来调整转子速比。示踪剂(少组分)放置在混合腔B侧。随速比的增加,即B腔转子转速增大,其内示踪剂混合均匀性得到提高,但左右两腔速比增大限制了两腔内的物料交换,所以从整体区域内示踪剂均匀性来看,随速比增大整体均匀性呈现先提高再降低的变化趋势。
1.3.2 混合时间的影响
在我们之前的研究中发现[11],随着混合时间的增加,示踪剂的均匀性提高,但混合的效率会逐渐降低,当混合时间达到一定长度后,混合均匀性指标基本保持不变。同时,在设定间歇式混合器工作时间时,也要考虑物料的热经历,过长的加热时间,会导致高分子降解,从而影响制品性能。
1.3.3 填充率的影响
填充率也是影响混合效果的重要因素。A. Chaisur iyathepkul等人[1]发现在填充率为60%~80%的范围内,随填充率的增加分散相在基体中变得粗大,混合效果变差。这可能与EPDM在NR的分散过程中黏性热有关,填充率的增加导致剪切生热增大,物料黏度降低,使得少组分团聚现象显著。在我们的研究中[10],扩大了填充率的研究范围。当填充率较低时(25%),物料黏附在转子表面,混合效果较差。随着填充率的增加(35%~75%),两腔内物料交换明显改善。但填充率过高时(约100%),型腔内物料自由流动空间降低,又限制了物料的交换。
2 混合性能评价指标体系
在流体动力学计算结果的基础上,结合张量计算和统计分析,研究人员构建了多种可用于评价混合器流场中流体混合性能的评价指标。
2.1 基于场量和间接指标的分析
2.1.1 基于速度场和压力场的分析
速度场和压力场是求解N-S方程直接得到的结果。在流场分析中具有至关重要的作用。通过压力场与速度场结合分析,可以发现流体从高压区经过转子与内壁的间隙回流到低压区。而回流是增强分布混合的有效途径之一[12],回流代表分布混合而切向流代表分散混合[13]。通过对速度场和压力场的分析,Connelly等人[5]发现双转子的转子两侧速度要比转子的切向圆周速度高得多,证明双转子混合器内不仅有拖曳流的存在还有压力流的存在。同时,S. A. Salahudeen等人[2]在速度矢量图中观察两个型腔内物料是如何相互交替流动的;也判断了哪些区域发生了
物料的交换,是混合的有效面积,哪些区域没有物料交换,只是随着转子一起转动,这部分物料称作塞流,混合器这部分区域称作死区。
2.1.2 基于间接指标的分析
扭矩代表着能量的输入,在间歇式混合器内,扭矩的变化可以描述物料特性的变化,其中就包括熔融、塑化以及混合等因素。在S. A. Salahudeen等人[2~3]的研究中,扭矩随时间的变化为先逐渐增大到某一峰值,然后开始回落至稳态,扭矩增大这一过程代表着越来越多的聚合物完全熔融成为黏弹性流体,而后趋于稳态[14]。
2.2 基于流场参数统计指标的分析
随着数值模拟计算水平的不断提高,越来越多的研究人员通过计算模拟来探究混合器的混合性能,同时也提出了很多用于评价混合性能的量化指标。值得注意的是,无论是衡量分散混合还是分布混合,单独使用某一项量化指标往往是片面的。在实际应用中需要综合全面考虑。
2.2.1 分离尺度
分离尺度可有效的描述分布混合性能:

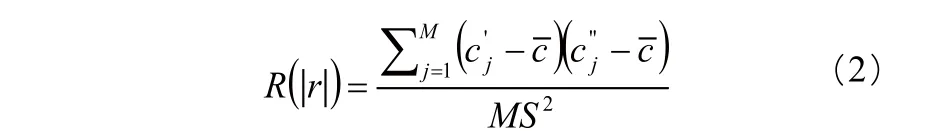
式中, Cj'和C'j'分别为第j对粒子点的浓度,C为所有M对浓度的平均值, S为样本标准差,M为间隔距离为r的粒子对的总数。分离尺度的初始数值与混合器几何尺寸及示踪粒子的初始布置有关。随着混合的发生S(t)减小,其减小速率可表示分布混合的效率,同时,S(t)曲线最终数值则表明混合的分布混合能力。分离尺度越小,分布混合效果越好[5,15]。
2.2.2 分布指数(DI)
示踪粒子初始团聚在一个小的区域内,随着混合的发生,粒子分布到整个混合区域中。统计不同时刻示踪粒子间距的概率密度函数f1,并与最优分布状态进行对比fopt:
1

式中,δ(t) 即为分布指数[16,17]。分布指数不仅和转子的形状有关,也和示踪粒子初始放置的位置有极大关联。放在塞流区域,则大部分示踪粒子随着转子一起转动,并不会发生有效的分布混合;而只有示踪粒子进入剪切比较强烈的区域,分布混合效果才会变得优异[2,5,6,15,18]。
2.2.3 拉伸长度
给定一个运动[19]:

其中X为物料某点在0时刻的位置,x为该点在t时刻的位置。0时刻无穷小线段长度dx与t时刻的长度 dX的关系为:

其中F为变形梯度张量,定义式为:

则拉伸长度 定义公式为:
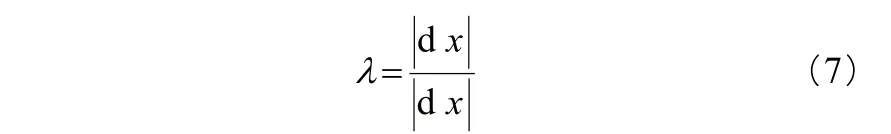
在整个混合过程及混炼区域内, 越高代表越好的混合质量。Connelly等人[5]通过对比混合过程中拉伸长度对数数值logλ变化发现,双转子混合器内logλ成线性增长趋势,而在单转子混合器内随时间增长logλ趋于平稳,他们指出,流体在双转子混合器中两转子间的折叠使得拉伸随时间成指数增长。Salahudeen等人[2]在对比Cam、Banbury、Roller三类转子的混合性能时也使用拉伸长度指标作为量化依据。
2.2.4 混合效率
在定义λ的基础上,瞬时混合效率可定义为[20]:

式中,D为变形速率张量。瞬时效率持续保持正值代表聚合物流体在滑动和折叠的过程中不断地重新取向和持续拉伸[2,3]。
进一步,可定义时间平均混合效率:

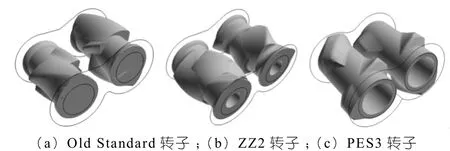
在间歇式混合器中, 2.2.5 面积拉伸比 当某平面微元在混合器中流动,受剪切和拉伸作用。为了量化这一效果,假设X位置有一虚拟粒子的 无限小面积为dA,在t时刻,粒子移动到x位置,并且变形和重取向为da,面积拉伸比可表示为[18]: 其中,N为dA的法线方向。利用这一指标Avalosse等人[18]对比了三维转子形状的混合性能。他们指出当该指标的平均值较大,且标准差较小,则该转子结构的混合性能则较为优异。 2.2.6 区域内物质交换 将混合区域划分为区域,并在这些区域内布置示踪粒子,随着混合的发生,记录示踪粒子轨迹,并统计在一定时间内未曾离开初始所在的腔体的粒子个数,那么也就得到了离开初始腔体至少一次的示踪粒子的个数,由此可以描述区域内的物质交换。当混合转子有足够的能力使得各个区域间具有充分的物质交换,则该转子结构设计将更加有效[18]。 2.2.7 区域分布指数 将混合器分为若干个相连且不重叠的区域。分别计算在指定区域内示踪粒子距离分布的概率密度f(z)和最优分布的概率密度fopt(2),并由此计算区域内t时刻的区域分布指数[18]: Avalosse等人[18]利用这一指标作为量化密炼机转子轴向分布均匀性的指标。他们沿转子轴向将混合区域进行分区,发现如图3所示PES3型转子的轴向分布均匀性>ZZ2型>OS型。 图3 文献[18]中的转子结构 2.2.8 混合指数 混合指数用来描述流场区域内流动的形式,其定义为[17]: 式中, D为变形速率张量,λ为涡旋张量。当λ=0时,流动模式为塞流;当时λ=1,流动模式为纯拉伸流动;当λ=0.5时,流动模式为纯剪切流动。虽然剪切流动是混合器中流体的主要流动形式,但研究表明在分散混合中拉伸流动的存在比纯剪切流动更有效,尤其是在高黏度和低界面张力的情况下[21~22],这一现象更为显著。此外,研究表明剪切变稀会使混合指数下降导致塞流区域增加,而黏弹性流体会增加拉伸流动区域的尺寸[6]。 2.2.9 混合过程中物料经历的最大剪切应力 少组分分散相在基体内的分散需要有足够的剪切应力。在间歇式混合器内存在高剪切区和低剪切区,只有少组分分散相流经高剪切区,才有可能发生破碎。在计算中,记录示踪微元在流场内经历的剪切应力,统计示踪微元经历的最大剪切应力的分布状态。这是衡量分散混合效率的有效工具。这不仅可以评价混合器的混合能力[5],而且可以预测少组分分散相在基体内的粒径分布状态[18]。 本文总结了近年来有关间歇式混合器混合性能研究的文献,介绍了间歇式混合器混合性能的研究现状,并归纳了混合器转子结构和工艺条件对混合器混合性能的影响规律。又从数值模拟统计分析的角度,对构成混合器混合性能评价指标体系中各个指标的应用情况进行一一介绍,这些指标是在数值模拟方面直观的评价了分布混合和分散混合,也对揭示实验中所产生的现象具有很大的帮助。本文综述内容对混合器的优化设计和数值量化评价将有一定指导意义。 ∶ [1] Chaisuriyathepkul A, Suchiva K, Sae-Oui P, et al. Mixing efficiency in co-rotating batch mixer for preparation of NR/ EPDM blends[J]. Journal of Applied Polymer Science, 2012, 123(6)∶3 688~3 695. [2] Salahudeen S A, Elleithy R H, Alothman O, et al. Comparative study of internal batch mixer such as cam, banbury and roller∶ Numerical simulation and experimental verification[J]. Chemical Engineering Science, 2011, 66(66)∶2 502~2 511. [3] Salahudeen S A, Alothman O, Elleithy R H, et al. Optimization of rotor speed based on stretching, efficiency, and viscous heating in nonintermeshing internal batch mixer∶ Simulation and experimental verification[J]. Journal of Applied Polymer Science, 2013, 127(4)∶2 739~2 748. [4] Prakash S, Kokini J L. Estimation and prediction of shear rate distribution as a model mixer[J]. Journal of Food Engineering, 2000, 44(3)∶135~148. [5] Connelly R K, Kokini J L. Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking[J]. Journal of Food Engineering, 2007, 79(3)∶ 956~969. [6] Connelly R K, Kokini J L. The effect of shear thinning and differential viscoelasticity on mixing in a model 2D mixer as determined using FEM with particle tracking[J]. Journal of Non-Newtonian Fluid Mechanics, 2004, 123(1)∶1~17. [7] Jongen T. Characterization of batch mixers using numerical flow simulations[J]. Aiche Journal, 2004, 46(11)∶2 140~2 150. [8] Tadmor Z, Gogos C G. Principles of polymer processing[M]. John Wiley & Sons, 2013. [9] Edwards M F. Chapter 11–Laminar flow and distributive mixing[J]. Mixing in the Process Industries, 1997∶200~224. [10] 郭少龙, 杨静, 毕超. 转子相对旋转方向对双转子混合器混合性能的影响[J]. 工程塑料应用, 2016(1)∶81~84. [11] 郭少龙.周期性变化速比双转子混合器混合性能的研究[D].北京:北京化工大学, 2016. [12] Bravo V L, Hrymak A N, Wright J D. Study of particle trajectories, residence times and flow behavior in kneading discs of intermeshing co-rotating twin-screw extruders.[J]. Polymer Engineering & Science, 2004, 44(4)∶779~793. [13] Yerramilli L, Karwe M V. Velocity Distributions and Mixing in the Translational Region of a Kneading Section in a Corotating Twin-screw Extruder[J]. Food & Bioproducts Processing, 2004, 82(1)∶5~12. [14] Shih C K, Tynan D G, Denelsbeck D A. Rheological properties of multicomponent polymer systems undergoing melting or softening during compounding[J]. Polymer Engineering & Science, 1991, 31(23)∶1 670~1 673. [15] Connelly R K, Kokini J L. Mixing simulation of a viscous Newtonian liquid in a twin sigma blade mixer[J]. Aiche Journal, 2006, 52(10)∶3 383~3 393. [16] Wong T H., MANAS-ZLOCZOWER, I. Two-Dimensional Dynamic Study of the Distributive Mixing in an Internal Mixer[J]. Intern. Polymer Proc,1994,9∶3~10. [17] Yang H H., MANAS-ZLOCZOWER, I. ANALYSIS OF MIXING PERFORMANCE IN A VIC MIXER[J]. International Polymer Processing, 1994, 9(4)∶291~302. [18] Avalosse T, Alsteens B, Legat V. Rotor shape design by numerical simulation∶ a new way to improve dispersive and distributive mixing in batch mixers[J]. Elastomery, 2005, 9(specjal)∶ 16~24. [19] Ottino J M, Ranz W E, Macosko C W. A framework for description of mechanical mixing of fluids[J]. Aiche Journal, 1981, 27(4)∶565~577. [20] Ottino J M. The Kinematics Of Mixing∶ Stretching, Chaos, And Transport[M]. The kinematics of mixing ∶ stretching, chaos, and transport. Cambridge University Press, 1989. [21] Elmendorp J J. A study on polymer blending microrheology[J]. Polymer Engineering & Science, 1986, 26(6)∶418~426. [22] Elemans P H M, Bos H L, Janssen J M H, et al. Transient phenomena in dispersive mixing[J]. Chemical Engineering Science, 1993, 48(2)∶267~276. Investigation of batch mixer’s mixing performance and the construction of evaluation system of mixing performance Investigation of batch mixer’s mixing performance and the construction of evaluation system of mixing performance In this paper, research literature on the mixed performance of the batch mixer is summarized; the influence of rotor structure and process conditions on mixing performance of the mixer is studied; the application of each index in the mixed performance evaluation index system of the mixer is analyzed from the point of view of numerical simulation and statistical analysis. Summary of the content will have a certain guiding significance for mixer optimization design and numerical evaluation. batch mixer; mixing performance; numerical simulation; evaluation index system Li Qinghuan, Bi Chao ( Beijing University of Chemical Technology, Beijing 100029, China) TQ320.64 1009-797X(2016)22-0007-05 B DOI∶10.13520/j.cnki.rpte.2016.22.003 (R-03) 李青寰(1992-),男,硕士研究生,主要从事聚合物加工的研究。 2016-09-12
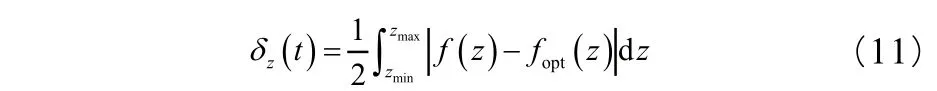
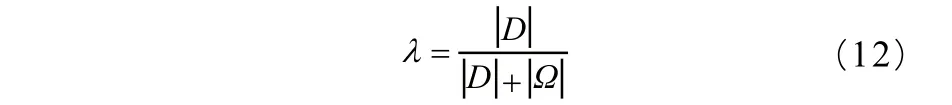
3 结论

