基于MMSE和LS的脉冲压缩技术

詹 旭, 帅晓飞, 罗 毅, 马 将

(1.四川理工学院自动化与电子信息学院, 四川 自贡 643000;2.零八一电子集团有限公司中国兵器装备集团(成都)火控技术中心, 成都 611731)



基于MMSE和LS的脉冲压缩技术

詹 旭1, 帅晓飞2, 罗 毅1, 马 将1

(1.四川理工学院自动化与电子信息学院, 四川 自贡 643000;2.零八一电子集团有限公司中国兵器装备集团(成都)火控技术中心, 成都 611731)

讨论了发射信号为复合波形时两种脉冲压缩技术：基于最小均方误差(MMSE)的自适应脉冲压缩技术和基于最小二乘(LS)的脉冲压缩技术。详细给出了这两种脉压技术的理论推导过程、具体特点。并通过仿真结果进一步阐述了这两种脉压技术的特点以及与传统的匹配滤波的异同。

自适应脉冲压缩;MMSE;LS;LFM

引 言

当发射信号为LFM信号时，传统的脉冲压缩就是匹配滤波。然而，LFM脉冲压缩信号处理技术存在距离分辨力与较低的压缩脉冲旁瓣电平不能兼得的矛盾，并且大目标回波的旁瓣会淹没临近距离单元的弱小目标，造成较高的漏警[1-5]。另外，在实际的雷达信号处理中，会遇到发射信号不是LFM信号的情况，此时若再用传统的匹配滤波，可能会产生更高的旁瓣。

鉴于上述情况，自适应脉冲压缩技术能有效地解决上述问题。

1 回波模型

雷达回波可以看成是目标RCS与雷达发射信号的乘积，由于发射信号是大时宽的信号，因此第l个距离单元的回波会受到附近距离单元的照射物体的影响。第l个距离单元的回波可以表示成：

y(l)=xT(l)s+n(l)

(1)

其中，y(l)表示第l个距离单元的回波；x(l)=x(l) x(l-1) … x(l-N+1)]T表示被照射物体的RCS值；n(l)表示高斯白噪声；s=s0s1… sN-1]T是发射信号。由上式可推导第l个距离单元的匹配滤波输出为：

yMF(l)=sHAT(l)s+sHn(l)

(2)

其中，yMF(l)表示匹配滤波器第l个距离单元的输出值；n(l)和A(l)分别表示：

n(l)=[n(l)n(l+1)…n(l+N-1)]T

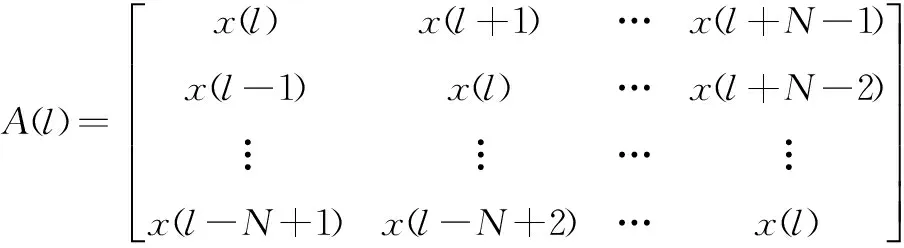
由式(2)可知，当对回波进行匹配滤波时，第l个距离单元的输出会包含前后N-1个距离单元的目标信息。当这些邻近距离单元有较大RCS目标时，就会淹没第l个距离单元的弱小目标

2 失配的脉冲压缩技术

2.1 基于MMSE的自适应脉冲压缩算法

为了正确估计目标的信息，可采用基于最小均方误差(MMSE)准则的自适应脉冲压缩技术。即用自适应的权值w(l)代替s*，具体地，基于式(1)可得第l个距离单元的代价函数：

(3)

其中，E[·]表示期望；w(l)=[w(l)w(l+1)…w(l+N-1)]T表示自适应的脉冲压缩技术权值。计算式(3)中的滤波器系数等价于解下列偏微分方程：

经过计算可得：

w(l)=(E[y(l)yH(l)])-1E[y(l)x*(l)]

假设目标的冲激响应与噪声是不相关的，再结合式(1)，上式可转变为：

(4)

其中，sn表示发射信号移动了n个样本的N×1维列向量。当n<0时，将发射信号左移，右边补零；当n>0时，将发射信号右移，左边补零。如s-2=[s2…sN-10 0]T，以及s2=[0 0s0…sN-3]T。

利用计算出的自适应滤波器系数w，第l个距离单元的自适应脉压输出可表示为：

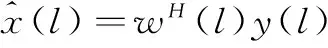
(5)

上述基于MMSE的自适应脉压是一个迭代计算滤波器系数的过程，并且由若干次实验结果表明迭代次数仅需2～3次就可获得很好的脉压效果。自适应脉压的初始值可由经典的匹配滤波输出得到。

2.2 LS脉冲压缩技术

式(1)中的回波数据还可以表示成：

yLS=Sx+v

(6)

式中，x=[x(0),x(1),…,x(l-1)]T表示在处理窗内的目标回波距离像；v=[v(0),v(1),…,v(l+N-2)]T表示l+N-1个噪声样本；而发射信号在回波中的存在形式可以表示成：

可以看出发射信号s=[s0,s1,…,sN-1]T是以矩阵S的形式出现在回波中，并且每一个距离单元的回波中都包含有其之前和之后若干个距离单元的回波成分。因此，某些距离单元若存在高强度的杂波或目标信号，就会掩盖附近距离单元的弱小目标信号，从而降低弱小目标的检测与跟踪性能。

从式(6)的表示出发，不难得到在最小方差(LS)准则下，最优滤波器权值为：WLS=(SHS)-1SH，于是目标回波距离像的最优估计为：

(7)

由式(7)估计出的目标距离像能够最大限度地抑制脉压带来的副瓣干扰。另外，WLS与传统的匹配滤波脉压技术一样，只由发射波形决定属于权值固定的脉压技术，可以事先计算，而不需适时计算，相对于wMMSE具有计算量小、易于工程实现的优点。然而，WLS只能处理l个距离单元的信号，而处理窗外的N-1个距离单元不能处理；再者，WLS不能抑制噪声，不能获得如匹配滤波的最大输出信噪比。

3 仿真实验

在实际工程中，常常会遇到某雷达分别用两个不同调频斜率、不同带宽以及不同中心频率的LFM发射信号。当该雷达想探测远距离目标时，结合两个不同的发射信号作为新的发射信号可以增加雷达作用距离。此时，传统的匹配滤波就面临着主瓣展宽、旁瓣增高的困难。因此，在该仿真过程中，假设当发射信号为复合波形时，分析不同脉压技术的输出结果。

给定两个发射信号为频带不连续、调频斜率不一样的线性调频信号：

s(t)=

其中，t1∈[0 15] μs，t2∈[15 20] μs，两个信号的频带分别为B1∈[-0.5 0.5] MHz，B2∈[1 2] MHz。其时域波形图和自相关函数分别如图1和图2所示：

图1 两个线性调频信号组成的复合信号时域波形

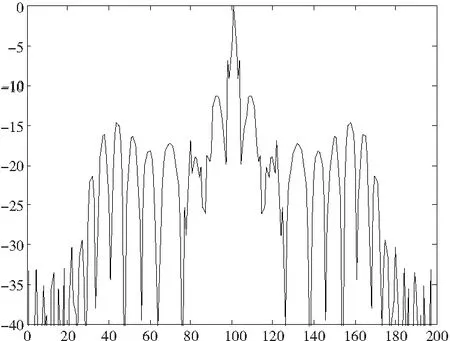
图2 图1所示波形的自相关函数

图2中的结果表明该复合波形的自相关函数有别于单个线性调频信号的自相关函数，其主瓣在大约-7 dB时出现分叉，并且具有若干个高旁瓣。因此，若采用经典的脉冲压缩算法，该复合信号的这些特点对雷达目标的检测极为不利。

假设在第1101个距离单元有个强目标(脉压前SNR=20 dB)、第1112个距离单元有个弱目标(脉压前SNR=0 dB)。对回波分别应用经典的脉冲压缩技术、基于MMSE和LS的自适应脉冲压缩算法进行仿真，结果如图3～图5所示。

图3 经典的脉冲压缩输出

图4 基于MMSE的自适应脉冲压缩技术输出

图5 基于LS的脉冲压缩输出

从图3中能够很明显地观察到图2所示的复合波形的自相关函数特点：主瓣展宽、旁瓣高增益。从图3所示的仿真结果可以看出，经过匹配滤波脉压后，噪声基底在30 dB左右，然而高达10 dB的旁瓣使第1112个距离单元的弱目标完全被第1101个距离单元的强目标旁瓣淹没，造成了弱小目标的漏警。另外，图3中的主瓣较宽，使得雷达的距离分辨力降低，对邻近距离单元的目标产生严重的遮蔽效应。

从图4的仿真结果可以看出，经过两次迭代后，基于MMSE的自适应脉压输出结果将旁瓣和噪声都抑制到了45 dB左右，而弱目标在20 dB左右，因此强目标的旁瓣得到有效抑制，能检测第1112个距离单元的弱目标。同时，经过该方法的自适应脉压后，主瓣变窄，这些现象都有利于强目标邻近距离单元的弱小目标检测，减小漏警。

由图5可以看出，复合波形的自相关函数的旁瓣得到了有效抑制，噪声基底在15 dB左右，弱目标比噪声基底高5 dB左右，因此能检测弱目标。对比匹配滤波和基于LS的脉冲压缩结果可以看出，图5中的噪声比图3中的强15 dB左右。这个现象也证明了当滤波系数是固定权值时，匹配滤波能获得最大的信噪比。

综合上述仿真结果，可以得出三种脉压技术的特点：

(1) 传统的匹配滤波脉压技术算法简单、易于实现，能获得较高的信噪比，但是旁瓣电平太高，强目标附近的弱目标无法检测。

(2) 基于MMSE的脉压技术能同时抑制噪声和旁瓣、发现弱小目标，但需要1～3次迭代才能获得较好的效果，并且每次迭代需要适时估计噪声加干扰协方差矩阵并求逆，计算量比较大。

(3) 基于LS的脉冲压缩技术权值固定、易于工程实现，能获得很好的旁瓣抑制效果，但是不能抑制噪声。

4 结 论

本文主要针对发射信号为复合LFM信号，传统脉压主瓣宽、旁瓣高、难以检测强杂波邻近距离单元的弱目标的问题，讨论了两种自适应脉冲压缩技术：基于MMSE的自适应脉冲压缩和基于LS的脉冲压缩技术。基于MMSE算法旁瓣低、抑制噪声能力强的特点，能有效地发现强目标相邻的弱小目标，但计算量比较大、难以工程实现；基于LS的脉冲压缩技术的权值固定、易于实现，能有效抑制旁瓣凸显强目标附近的弱目标，但没有抑制噪声的能力。

综合仿真结果及分析，得出以下结论：

(1) 当雷达系统对实时性要求不高，并且硬件条件比较好时，可以选用基于MMSE的脉压技术，该技术能能有效地抑制噪声、使主瓣变窄并压低旁瓣凸显弱小目标，提高雷达检测性能。

(2) 当检测对象为噪声中的弱小单个目标，且噪声基底高于发射波形的第一旁瓣时，选用匹配滤波能获得比较好的结果。

(3) 当雷达需要关注强目标附近的弱小目标，且环境噪声低于发射波形的旁瓣时，宜选用基于LS的脉冲压缩技术。

[1] 解虎,冯大政,虞鸿波,等. 一种采用稀疏表示的快速空时自适应方法[J].西安电子科技大学学报,2015(5):15-30.

[2] ZHANG J,DRINKWATER B W,WILCOS P D.Comparison of ultrasonic array imaging algorithms for nondestructive evaluation[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2013,60(8):1732-1745.

[3] 王强,袁慎芳,陈小惠,等.主动Lamb波合成波阵面损伤成像监测方法[J].仪器仪表学报,2011,32(11):2468-2474.

[4] 余业林.基于超声阵列成像的无损检测[D].广州:华南理工大学, 2012.

[5] 王平,邹强鑫,王林泓,等.一种融合动态孔径的聚焦延迟参数压缩方法[J].仪器仪表学报,2013,34(9):2080-2086.

[6] 焦敬品,于兆卿,刘文华,等.基于小波变换的薄层厚度电磁超声测量方法[J].仪器仪表学报,2013,34(3):588-595.

[7] 杨虎,陈航,戚茜.一种用于水下声成像的旁瓣抑制方法[J].西北工业大学学报,2009,27(2):209-213.

[8] GUO J Z,XIN Y H.Reconstructing outside passband data to improve time resolution in ultrasonic detection[J].NDT and E International,2012,50:50-57.

[9] LI X,LI X B,LIANG W,et al.0-Norm regularized minimum entropy deconvolution for ultrasonic NDT & E[J].NDT and E International,2012,47:80-87.

Pulse Compression Technology Based on MMSE and LS

ZHANXu1,SHUAIXiaofei2,LUOYi1,MAJiang1

(1.School of Automation and Electronic Information, Sichuan University of Science & Engineering, Zigong 643000, China; 2.China South Industries Group Fire Control Center, The 081 Electronics Group Co.,Ltd., Chengdu 611731, China)

Two pulse compression technologies, MMSE and LS, are studied when the transmit signal in a composite waveform. The theoretical derivation and specific features of the two pulse compression technologies are given in detail. The results of the simulation elaborate the difference from other conventional matched filter and the characters of the two pulse compression technologies.

adaptive pulse compression; MMSE; LS; LFM

收稿日期：2015-05-20

国家自然科学基金项目(61178068);四川省教育厅基金项目(14ZB0223)

詹 旭(1981-),女,四川宜宾人,讲师,硕士,主要从事信号与信息处理、图像处理方面的研究,(E-mail) zhanxuu@163.com

1673-1549(2016)01-0029-04

10.11863/j.suse.2016.01.07

TN958.6

A