基于蒙特卡洛模拟的极限注水压力不确定性分析

武胜男， 张来斌， 邓金根， 曹砚锋， 文 敏

(1.中国石油大学(北京)机械与储运工程学院，北京 102249；2.油气资源与探测国家重点实验室(中国石油大学(北京)，北京 102249；3.中海油研究总院，北京 100028)



基于蒙特卡洛模拟的极限注水压力不确定性分析

武胜男1， 张来斌1， 邓金根2， 曹砚锋3， 文 敏3

(1.中国石油大学(北京)机械与储运工程学院，北京 102249；2.油气资源与探测国家重点实验室(中国石油大学(北京)，北京 102249；3.中海油研究总院，北京 100028)

海上油田注水过程中，为防止由于注水压力不合理而导致盖层完整性被破坏，需要对极限注水压力的不确定性及敏感因素对其的影响规律进行分析。以PL19-3油田某注水井为研究对象，利用FLAC3D软件建立了储盖层模型，模拟计算了盖层开始发生破坏时的注水压力即极限注水压力，分析了渗透率、内聚力和内摩擦角等参数对极限注水压力的影响，并采用蒙特卡洛模拟方法分析了极限注水压力的不确定性。结果表明：当注水压力达到极限注水压力时，盖层开始发生破坏；随着渗透率增大，极限注水压力呈现出先增大后减小再缓慢增大的趋势；随着内聚力和内摩擦角的增大，极限注水压力分别呈现线性增大和二次函数增大的趋势。确定性极限注水压力只是不确定性分析结果的一部分，而通过不确定性分析可以得到盖层发生破坏可能性较大的极限注水压力区间，能够对极限注水压力进行全面评估，可以为现场注水安全管理提供理论指导。

注水压力；蒙特卡洛模拟；不确定性；渗透率；内聚力；内摩擦角

在低渗透油田注水开发过程中，通常通过提高注水压力在地层堵塞处形成微裂缝，增大注水量，从而达到提高采收率的目的。但注水压力不可能无限制地提高，如果注水井的井底压力很高，注入水可能突破盖层，窜入其他层位造成注水层间干扰，影响注水开发效果；也可能进入泥页岩层，引起泥页岩水化膨胀,从而挤毁套管。例如蓬莱19-3B油田注水过程中由于注入压力过高形成地层超压乃至破裂，导致严重的溢油事故，造成了严重的经济损失，同时给环境和社会带来了巨大的危害[1]。因此，确定注水压力界限时应充分考虑盖层的完整性和有效的微观封闭能力[2-3]。

一些学者开展了关于不同地质条件下注水压力界限的研究和探讨[4-5]，但对注水过程中导致盖层破坏的注水压力界限和地层不确定性因素对注水压力影响的研究相对较少。传统确定注水压力界限的方法都基于地层破裂压力，注水井井底压力必须严格控制在破裂压力以下，或取注水井地层破裂压力的 80%～90%作为注水井最大允许井底压力[6]，但该方法确定的注水压力并不一定能够确保盖层不被破坏，并且不能评估地层不确定因素对注水压力的影响。因此，笔者定义海上油气田注水过程中致使盖层开始发生破坏的注水压力为极限注水压力(extreme injection pressure，EIP)，即注水井可以达到最高的井底压力，利用FLAC3D软件建模计算极限注水压力，采用蒙特卡洛模拟(Monte Carlo simulation，MCS)方法分析地层不确定因素对极限注水压力的影响。

1 极限注入压力的确定

FLAC3D是一种基于拉格朗日差分法的三维显式有限差分程序，已经广泛应用于工程地质、岩土力学以及构造地质学和矿山工程领域，适宜处理大尺度、大变形工程和地质问题[7]。该软件能够实现多种材料模式的求解和不规则边界条件的连续性问题求解，可以精确模拟材料的屈服和塑性流动状态。注水过程中，盖层初始发生的破坏为剪切破坏，因此，应用FLAC3D软件研究盖层开始发生剪切破坏时的井底压力。

1.1 计算模型及参数的确定

1) 在分析注水井资料的基础上，利用FLAC3D软件提供的网格生成器建立储盖层应变模型。

2) 由于计算结果的可靠程度与岩石力学参数和原岩应力等参数有关，因此根据模拟计算区域的岩层结构和岩石力学参数确定模型的基本参数。岩体变形参数采用反映材料基本特性的体积模量和剪切模量[8]，可以将弹性模量(或变形模量)和泊松比转化为体积模量和剪切模量，公式如下：

(1)

(2)

式中：K为体积模量，MPa；E为弹性模量，MPa；μ为泊松比；G为剪切模量，MPa。

3) 强度准则的确定。盖层属于弹塑性体，当荷载达到屈服强度后盖层将发生破坏、弱化。笔者选取摩尔-库仑准则和弹塑性本构关系作为强度准则。摩尔-库仑准则为：

(3)

式中：fs为剪切破坏阈值，Pa；σ1和σ3分别为最大主应力和最小主应力，Pa；C为岩石的内聚力，Pa；φ为岩石的内摩擦角，(°)。

当fs大于0时，岩石不发生剪切破坏；当fs小于0时，岩石将发生剪切破坏。当岩石单元体达到屈服极限后，在稳定应力下产生塑性变形；在拉应力状态下，当拉应力超过岩体抗拉强度时，岩体将发生拉伸破坏。

1.2 模型边界条件的确定

采用软件建立储盖层模型时，需要确定的边界条件为：

1) 施加初始地应力和初始孔隙压力；

2) 储层部位以恒定压力注水；

3) 盖层内边界为非渗透边界，外边界为定压边界；

4) 固定模型四周的法向位移。

将参数输入模型模拟计算不同井底注水压力时盖层的破坏状态，得到盖层发生初始破坏时的井底注水压力，即极限注水压力。该方法确定的极限注水压力必须不大于该区块的地层破裂压力。

2 不确定性分析方法

2.1 蒙特卡洛模拟

MCS方法[9]以概率统计理论为基础，能准确分析各种不确定性因素的影响。该方法通过确定随机变量的概率密度函数，从概率分布中重复抽样建立输出变量的分布，对输出结果进行统计，并拟合输出结果的概率分布情况。

2.1.1 概率密度函数的确定

在MCS抽样中，实际资料统计表明，地质数据多数情况下呈三角形分布或正态分布[10]。三角形分布通过判断分析确定变量的最小值a、最可能值c和最大值b来决定整个分布，目前已经广泛应用于概率风险模拟分析之中。服从三角形分布的概率密度函数为：

(4)

若随机变量x服从一个数学期望为μ、方差为σ2的高斯分布，则可以用正态分布来模拟。正态分布N(μ,σ2)的概率密度函数为：

(5)

2.1.2 概率分布模拟

为了解决盖层破坏时极限注水压力的概率分布问题，给出一定目标区的盖层破坏概率计算公式：

(6)

式中：P为盖层破坏时极限注水压力的概率；g(x)为与极限注水压力有关的函数；f(x)为概率密度函数。

由式(6)可知，破坏概率的计算很难利用解析方法解决，因此采用MCS方法解决该类问题。从概率分布f(x)中抽出N个子样x1，x2，…，xn，则盖层破坏时极限注水压力的概率为：

(7)

Crystal Ball 软件中的MCS模块可以用来进行各种方案的风险预测与不确定模型的研究[11]。因此，笔者利用Crystal Ball 软件中的MCS模块分析地层不确定因素对极限注水压力的影响。

2.2 参数不确定性分析步骤

由于部分储盖层物性参数和岩石力学参数存在不确定性，因此盖层的破坏以及极限注水压力也存在不确定性。参数的不确定性[12]主要来源于测量误差、采样误差、地质环境改变等，笔者在此主要讨论计算极限注水压力时所涉及到的参数，并进行不确定性研究。不确定性分析步骤为：

1) 分析储盖层的岩石力学参数的不确定性，确定对计算极限注水压力影响较大的岩石参数。

2) 分析不确定性参数对极限注水压力的影响规律，通过多项式拟合建立极限注水压力与不同参数之间的函数关系式。利用决定系数R2表征拟合方程的拟合程度，R2越接近1，表明极限注水压力与不同参数之间的拟合程度越高。

3) 确定不同岩石参数的概率密度函数，并开展参数的不确定性分析。

4) 确定模拟次数，运用Crystal Ball 软件进行模拟计算。

5) 统计计算结果，绘制概率分布图，预测不同参数下极限注水压力的概率分布区间。

3 应用实例

选取蓬莱19-3油田某注水井作为研究对象，其注水层位为L40—L70油组。蓬莱19-3油田注水井井深1 100.00～1 300.00 m，不考虑各层的差异性，储盖层参数取该油田一般值。该油田上覆岩层压力为24.0 MPa，原始地层孔隙压力为11.0 MPa，最大水平主应力为22.2 MPa，最小水平主应力为16.5 MPa。

根据PL19-3油田某井现场钻井完井报告、油田地层物性及岩石力学分析结果，假设盖层是完整的(没有原生裂缝或断层)，计算突破盖层时的注水压力。储盖层的参数见表1。

表1 PL19-3油田某井储盖层的参数

Table 1 Reservoir-caprock parameters of a well in PL19-3 Oilfield

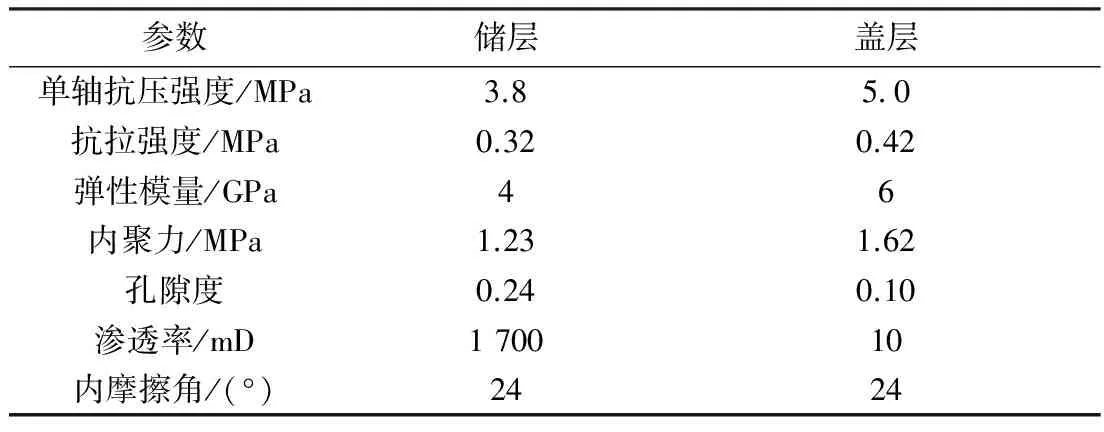
参数储层盖层单轴抗压强度/MPa3．850抗拉强度/MPa0．320．42弹性模量/GPa46内聚力/MPa1．231．62孔隙度0．240．10渗透率/mD170010内摩擦角/(°)2424

3.1 极限注水压力的计算

3.1.1 模型的建立

利用FLAC3D软件建立储盖层模型如图1所示，模型尺寸(长、高、厚)50.0 m×0.2 m×30.0 m，包括上盖层、储层、下盖层各10个单元。不考虑井眼影响，储层部位以恒定压力注水，盖层内边界为非渗透边界，外边界为定压边界，同时固定模型四周的法向位移。

3.1.2 模拟结果分析

图2为通过模拟计算得到的注水时盖层发生剪切破坏的情况(图中蓝色区域代表储盖层未发生剪切破坏，粉色区域代表储盖层已经发生破坏)。

图1 储盖层模型Fig.1 Caprock model

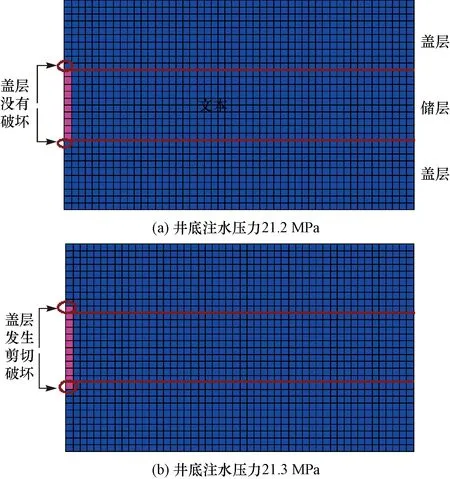
图2 不同井底注水压力下盖层剪切破坏状态Fig.2 Shear failure state of cap for different bottom hole injection pressure

从图2可以看出：当井底注水压力为21.2 MPa时，储层区域发生破坏，而盖层均未发生破坏；当井底注水压力为21.3 MPa时，储层和盖层的接触面开始发生破坏。这表明，随着井底注水压力增大，盖层由最开始的不发生破坏到破坏区域逐渐增大；若再继续提高注水压力，盖层区域将进一步被破坏，可能出现突破盖层的风险。从图2还可以看出，极限注水压力为21.3 MPa，由于该油田的地层破裂压裂为24.0 MPa，满足极限注水压力小于地层破裂压力的要求。

3.2 不确定性分析

实际注水过程中，极限注水压力的求取受到地层不确定性参数的影响，这些不确定参数包括单轴抗压强度、抗拉强度、弹性模量、内聚力、内摩擦角、渗透率和孔隙度等地层参数。这些参数随地质构造在某一范围内随机变化，很难用具体数值表征，且部分参数之间具有相关性，比如内聚力受到单轴抗压强度、抗拉强度、弹性模量等影响，渗透率与孔隙度相关，因此需要开展不确定因素的敏感性分析。笔者在假设其他参数不变的情况下，分析了内聚力、内摩擦角和渗透率对极限注水压力的影响。

3.2.1 不同参数对极限注水压力的影响

通过解释测井资料得知该油田储层渗透率的变化范围为500～3 000 mD，内聚力变化范围为1.4～3.0 MPa，内摩擦角变化范围为20°～36°。假设其他参数不变，在上述范围内分析不同变量的取值对极限注水压力的影响。

根据模拟结果，绘制极限注水压力与渗透率、内聚力和内摩擦角的关系曲线，如图3所示。

图3 极限注水压力与渗透率、内聚力和内摩擦角的关系曲线Fig.3 Relationship of extreme injection pressure vs. permeability,cohesive force and internal friction angle respectively

从图3可以看出：随着地层渗透率增大，极限注水压力呈先增大后减小，再缓慢上升最后趋于稳定的趋势；随着内聚力增大，极限注水压力呈线性增大趋势；随着内摩擦角增大，极限注水压力增大。

对图3中极限注水压力与渗透率、内聚力和内摩擦角的关系进行拟合，得到：

10-6K2+3.8×10-3K+19.883

(8)

R2=0.978 9

pEIP=4.358 3C+14.412

(9)

R2=0.999 3

pEIP=-0.014 5φ2+1.100 5φ+3.254 8 (10)

R2=0.991 0

式(8)—式(10)的决定系数R2都大于0.970 0，表明这3个拟合关系式的拟合程度很高，可以利用这3个关系式预测该油田不同渗透率、内聚力和内摩擦角下的极限注水压力，以降低注水过程中发生突破盖层的风险。

3.2.2 参数不确定性分析

极限注水压力不确定性分析是根据渗透率、内聚力和内摩擦角的概率密度函数随机取值，带入式(8)—式(10)中求得极限注水压力，基于概率统计理论，应用MCS抽样计算得到具有一定概率分布的计算结果。通过测井资料解释可知，储层渗透率的最大值为3 000 mD，最小值为500 mD，最有可能出现的值为1 700 mD，则认为渗透率的概率密度函数服从三角分布。同理，内聚力的概率密度函数服从区间(1.4 MPa，1.6 MPa，3.0 MPa)的三角分布。内摩擦角随着地层的抗拉强度的变化而变化，假定其概率密度函数服从(30°，3°)的正态分布。确定渗透率、内聚力和内摩擦角的分布后，把极限注水压力定义为预测参数，采用直接抽样法设定抽样次数为10 000次，通过模拟计算统计极限注水压力的概率分布，结果见图4。

极限注水压力计算结果为21.3 MPa，与图4中渗透率、内聚力和内摩擦角所对应的概率分别为0.004 93，0.034 91和0.023 77，均在置信水平5%以下，说明盖层发生破坏的可能性比较小。由图4可知，置信水平5%～95%所对应的极限注水压力区间分别为(21.51 MPa，22.46 MPa)、(21.47 MPa，26.26 MPa)和(21.73 MPa，24.00 MPa)，即盖层发生破坏可能性较大的极限注水压力分布在上述区间。鉴于地层参数的不确定性，极限注水压力计算结果只是不确定性分析中的一部分，根据该结果很难准确评估盖层发生破坏的可能性，然而不确定性分析却能够对极限注水压力进行全面评估，可以为现场注水安全管理提供指导。

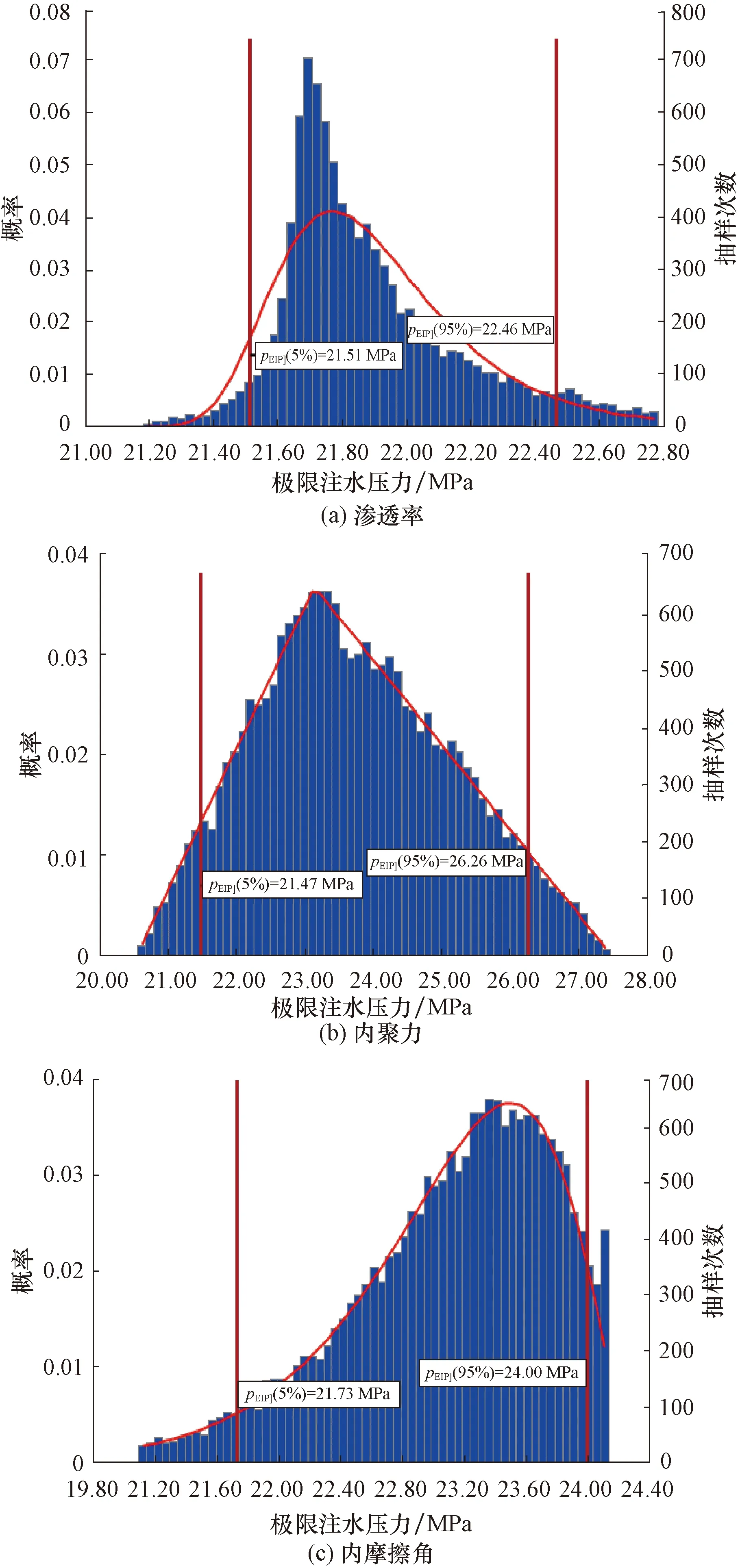
图4 渗透率、内聚力和内摩擦角对应极限注水压力的概率分布Fig.4 Probability distribution of extreme injection pressure corresponding to permeability, cohesive force and internal friction angle

4 结论及建议

1) 海上油田注水过程中盖层是否发生破坏与极限注水压力密切相关，当注水压力达到极限注水压力时，盖层开始发生破坏，若再继续提高注水压力，盖层将会被进一步破坏，可能出现突破盖层的风险。

2) 极限注水压力计算结果只是不确定性分析中的一部分，根据其很难准确评估盖层发生破坏的可能性，而不确定性分析可以得到盖层发生破坏可能性较大的极限注水压力区间，能够对极限注水压力进行全面评估，可以为现场注水安全管理提供理论指导。

3) 分析极限注水压力时，由于缺少大量的地质数据资料，只考虑了渗透率、内聚力和内摩擦角3个参数，进行了简单的分析。如果能获得详细的地质数据资料，可以拟合出更加符合实际的参数分布概率密度函数，进行更全面、准确的分析。

4) 建议将考虑盖层破坏的基于蒙特卡洛模拟分析极限注水压力不确定性的方法，推广到考虑断层开启、套管破坏的注水模型中，为海上油田注水提供更有价值的决策支持。

[1] WEI Lai，HU Zhuowei，DONG Lin，et al.A damage assessment model of oil spill accident combining historical data and satellite remote sensing information：a case study in Penglai 19-3 oil spill accident of China[J].Marine Pollution Bulletin，2015，91(1)：258-271.

[2] JIN Zhijun，YUAN Yusong，SUN Dongsheng.Models for dynamic evaluation of mudstone/shale cap rocks and their applications in the Lower Paleozoic sequences，Sichuan Basin，SW China [J].Marine and Petroleum Geology，2014，49:121-128.

[3] 黄学，付广，赖勇，等.断裂对盖层封闭性破坏程度定量研究[J].大庆石油地质与开发，2008，27(6)：5-9.

HUANG Xue，FU Guang，LAI Yong，et al.Quantitative research on destroy degree of caprock seal by faults[J].Petroleum Geology & Oilfield Development in Daqing，2008，27(6)：5-9.

[4] 曹广胜，谭畅，宋福昌，等.低渗透油田强化注水压力界限研究[J].科学技术与工程，2012，12(13)：3107-3110，3115.

CAO Guangsheng，TAN Chang，SONG Fuchang，et al.Pressure limit of enhanced water injection in low permeability oilfield[J].Science Technology and Engineering，2012，12(13)：3107-3110，3115.

[5] 赵永胜，陆蔚刚，兰玉波，等.多层砂岩油田水驱开发的合理注水压力[J].大庆石油地质与开发，2000，19(6)：21-24.

ZHAO Yongsheng，LU Weigang，LAN Yubo，et al.Reasonable water injection pressure of water flooding of multi-layer sandstone oil fields[J].Petroleum Geology & Oilfield Development inDaqing，2000，19(6)：21-24.

[6] 刘洪杰，陈鸿，王海更，等.海上复杂断块油田合理注水压力研究[J].断块油气田，2015，22(2)：228-233.

LIU Hongjie，CHEN Hong，WANG Haigeng，et al.Study on reasonable water injection pressure of offshore complex fault-block oilfield[J].Fault-Block Oil and Gas Field，2015，22(2)：228-233.

[7] 张书伟，林杭，任连伟.FLAC3D在岩土工程中的应用[M].北京：中国水利水电出版社，2011：83-107.

ZHANG Shuwei，LIN Hang，REN Lianwei.The application of FLAC3Dto geotechnical engineering[M].Beijing：China Waterpower Press，2011：83-107.

[8] 孙国权，李娟，胡杏保.基于FLAC3D程序的采空区稳定性分析[J].金属矿山，2007(2)：29-32.

SUN Guoquan，LI Juan，HU Xingbao.FLAC3D-based stability analysis of mined-out area[J].Metal Mine，2007(2)：29-32.

[9] 李春艳.利用蒙特卡洛模拟与风险分析优选水平井完井方式[J].石油钻探技术，2009，37(5)：52-57.

LI Chunyan.Applications of Monte Carlo simulation method and risk analysis in horizontal well completion optimization[J].Petroleum Drilling Techniques，2009，37(5)：52-57.

[10] 董玉亮，顾煜炯，杨昆.基于蒙特卡洛模拟的发电厂设备重要度分析[J].中国电机工程学报，2003，23(8)：201-205.

DONG Yuliang，GU Yujiong，YANG Kun.Criticality analysis on equipment in power plant based on Monte Carlo simulation[J].Proceedings of the Chinese Society for Electrical Engineering，2003，23(8)：201-205.

[11] 李帅芳，肖果平.Crystal Ball在项目管理风险分析中的应用[J].项目管理技术，2013，11(4)：40-44.

LI Shuaifang，XIAO Guoping.Application of Crystal Ball in project management risk analysis[J].Project Management Technology，2013，11(4)：40-44.

[12] HENLEY H，LUCIA A.Constant pressure Gibbs ensemble Monte Carlo simulations for the prediction of structure I gas hydrate occupancy[J].Journal of Natural Gas Science and Engineering，2015，26：446-452.

[编辑 刘文臣]

Monte Carlo Simulation-Based Uncertainty Analysis on Extreme Water Injection Pressure

WU Shengnan1, ZHANG Laibin1, DENG Jingen2, CAO Yanfeng3, WEN Min3

(1.College of Mechanical and Transportation Engineering, China University of Petroleum(Beijing), Beijing, 102249, China；2.State Key Laboratory of Petroleum Resource & Prospecting (China University of Petroleum(Beijing)), Beijing, 102249, China;3.CNOOC Research Institute, Beijing, 100028, China)

In order to avoid caprock integrity failure caused by unreasonable water injection pressure during water injection in offshore oil fields, it is necessary to conduct an uncertainty analysis on extreme injection pressure and the controlling influences of sensitive factors on extreme injection pressure. In this paper, a water injector in the PL19-3 Oilfield was taken as a research object and a caprock model was established by using FLAC3Dsoftware. Based on this model, the extreme water injection pressure (i.e. the water injection pressure when the caprock is initially broken) was calculated. Then, the effect of sensitive parameters (e.g. permeability, cohesive force and internal friction angle) on extreme injection pressure was analyzed. Furthermore, the uncertainty of extreme water injection pressure was studied by means of Monte Carlo simulation (MCS). It is shown that cap rocks begin to break when the extreme injection pressure is reached. As the permeability increases, extreme injection pressure varies, first in the trend of increasing, decreasing then increasing slowly. The extreme injection pressure increases linearly as the cohesive force increases, but in the form of quadratic function with the increasing of the internal friction angle. A deterministic result of extreme injection pressure is only a part of the uncertainty analysis. Through uncertainty analysis, the range of extreme injection pressure with higher probability of caprock failure can be revealed and extreme injection pressure can be evaluated comprehensively so as to provide the theoretical guidance in the secure management of water injection.

injection pressure; Monte Carlo simulation; uncertainty; permeability; cohesive force; internal friction angle

2015-07-13；改回日期：2016-02-14。

武胜男(1986—)，女，山西大同人，2010年毕业于青岛科技大学安全工程专业，2013年获中国石油大学(北京)安全技术及工程专业硕士学位，在读博士研究生，研究方向为海上工艺过程风险与海洋装备的可靠性。E-mail：wshn19@163.com。

中海石油(中国)有限公司科研攻关项目“注水井堵塞机理及增注降耗方法研究-解堵注水安全评价”(编号：CNOOC-KJ125ZDXM06LTD-08-ZY-12)部分研究内容。

◀油气开发▶

10.11911/syztjs.201603

TE921

A

1001-0890(2016)03-0109-06